Gorio Tech Blog search

펜윅 트리(Fenwick Tree, Binary Indexed Tree, BIT)

09 Jul 2018 | Fenwick Tree BIT

목차

참조

분류 URL
문제 구간 합 구하기, 구간 합 구하기 3
응용 문제 나무 심기
이 글에서 설명하는 라이브러리 fenwick_tree_BIT.h

개요

시간복잡도: $ O(M log N) $

구간 합 구하기: $ O(log N) $

값 업데이트하기: $ O(log N) $

공간복잡도: $ O(N) $

  • N은 원소의 수, M은 연산의 수이다.

이 글에서는 펜윅 트리(Fenwick Tree) 라고 하는 자료구조와, 이를 활용한 문제들을 살펴볼 것이다.

펜윅 트리라니? 라고 생각할지도 모르겠지만, 이는 여러분이 아마 들어본 적이 있을 Binary Indexed Tree(BIT)와 같은 것이다.

참고로 펜윅 트리로 풀리는 문제는 전부 인덱스 트리로도 풀린다.

펜윅 트리(Fenwick Tree, Binary Indexed Tree, BIT)

흔히 BIT라고 불리는 펜윅 트리(Fenwick Tree)는 ‘수시로 바뀌는 수열의 구간 합’을 빠르게 구할 수 있도록 고안된 자료 구조이다.

다음 상황을 살펴보자.

  • 길이 10만짜리 수열이 있다.
  • 12345~77777번 수들의 합을 구하라는 요청이 들어왔다. 65433개를 일일이 세어 합을 구해준다.
  • 똑같은 요청이 여러 번 들어오자. 여러분은 부분 합이라는 스킬을 써서 꼬박꼬박 답을 해 주었다.
  • 이번엔 20000번째 수와 55555번째 수를 업데이트하라고 했다.
  • 부분 합을 8만 개를 업데이트해야 하는 여러분은 화가 나기 시작했다.

…물론 이런 상황이 실제로 일어나지는 않겠지만, PS의 세계에서는 자주 있는 일이다. 누군가 무슨 숫자를 구해야 하고 그걸 여러분에게 자주 시키지 않는가?

이런 상황에서 펜윅 트리를 쓸 수 있다. 즉 수시로 바뀌는 수열의 구간 합을 $O(log N)$만에 구할 수 있다.

펜윅 트리는 다음과 같은 장점을 갖고 있다.

  1. 방금 말했듯이 업데이트가 하나씩 되는 수열의 구간 합을 $O(log N)$만에 구할 수 있다.
  2. 비트 연산을 이해하고 있다면 구현이 굉장히 쉬운 편이다.
  3. 속도도 빠르다(Big-O 표기법에서 생략된 상수가 작음).

그럼 펜윅 트리의 구조를 살펴보자.

펜윅 트리(BIT)의 구조

앞의 예를 조금 축소시켜서, 길이 10짜리 수열을 하나 생각하자. arr[]이라고 부르도록 하겠다.

01_부분합1

펜윅 트리는 개념상 트리이지만, 구현할 때는 길이 N짜리 배열로 구현한다.
정확히는 앞에 하나를 비워 두기 때문에 배열 자체의 크기는 $N+1$이고, 사용하는 인덱스는 1이상 N 이하이다.

그림에는 N=16일 때의 펜윅 트리가 그려져 있다. 배열의 경계 정하는 것이 헷갈리는 사람이라면 그림처럼 마음 편히 $2^n$ 꼴로 잡으면 된다.
하지만 펜윅 트리는 굳이 $2^n$ 꼴이 아니더라도 잘 작동한다. 이유는 이 글을 다 읽고 손으로 써 보면 알 수 있을 것이다.

앞으로 이 배열을 data[]라고 부르도록 하겠다. 필자의 코드에서 FenwickTree 클래스의 vector<int> data로 구현되어 있다.

02_FenwickTree1

이제 배열로 구현된 펜윅 트리의, data의 각 원소가 갖는 값을 살펴보자.

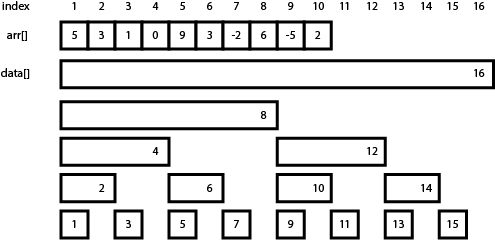
03_FenwickTree2

위 그림에 모든 것이 설명되어 있긴 하지만, 자세히 살펴보자. i는 0 이상인 정수이다.

  1. 인덱스가 홀수인 원소는 수열의 해당 인덱스의 값을 그대로 가진다.
    1. $data[2i+1] = arr[2i+1]$
    2. data[1] = arr[1], data[3] = arr[3], …
  2. 인덱스가 2의 배수이면서 4의 배수가 아닌 원소(2, 6, 10, 14, …)는 직전 두 arr 원소의 합을 보존한다.
    1. $data[4i+2] = arr[4i+1] + arr[4i+2]$
    2. data[2] = arr[1] + arr[2], data[6] = arr[5] + arr[6], …
  3. 인덱스가 $2^k$의 배수이면서 $2^{k+1}$의 배수가 아닌 원소는 직전 arr의 $2^k$개의 값의 합을 보존한다.
    1. $data[2^{k+1} \cdot i + 2^k] = \Sigma_{j=1}^{2^k}{arr[2^{k+1} \cdot i + j]}$
    2. data[12] = arr[9] + arr[10] + arr[11] + arr[12], …

수식이 조금 복잡할 수는 있지만 그림을 보면 바로 이해될 것이다.

구간 합($O(log N)$)

이제 이 data[]로 구간 합을 어떻게 빠르게 구하는지 알아보자. 예를 들어서 arr[1…7]의 합을 구한다고 하자.

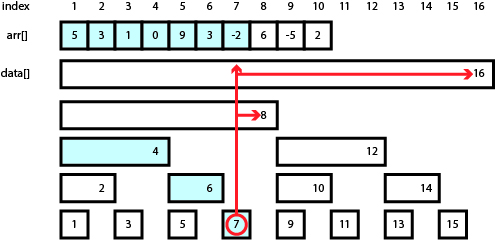
04_FenwickTree3

\[\Sigma_{j=1}^7{arr[j]} = \Sigma_{j=1}^4{arr[j]} + \Sigma_{j=5}^6{arr[j]} + \Sigma_{j=7}^7{arr[j]}\]

여기서 $\Sigma_{j=1}^4{arr[j]} = data[4]$, $\Sigma_{j=5}^6{arr[j]} = data[6]$, $\Sigma_{j=7}^7{arr[j]} = data[7]$ 임을 알았으면 여러분은 구간 합을 구하는 방법을 이해한 것이다.

N=10이라서 감이 잘 안 올 수는 있지만, 이렇게 구하는 방법이 $O(log N)$ 시간에 완료된다는 것도 알 수 있을 것이다.

아직 의문점이 좀 있을 것이다.

  1. 그럼 arr[4…12]의 합은 어떻게 구하는가?
    1. arr[1…12] - arr[1…3]을 구하면 된다. 즉, sum 연산을 두 번 실행하고, 작은 쪽을 빼 주면 끝.
  2. 눈으로 보면 arr[1…7] = data[4] + data[6] + data[7]인 것을 알 수 있지만, 구현은 어떻게 쉽게 하는가?
    1. 비트 연산을 이해한다면 구현도 굉장히 쉽다. 구체적인 예(arr[1…43])를 보자.
      1. arr[1…43] = data[32] + data[40] + data[42] + data[43]이다.
      2. 43을 이진법으로 나타내면 $101011_2$이다.
      3. 43의 LSB(1인 비트 중 끝자리)를 하나 뗀다. $101010_2 = 42$이다.
      4. 하나 더 떼 본다. $101000_2 = 40$이다.
      5. 하나 더 떼 본다. $100000_2 = 32$이다.
    2. 그럼 LSB를 어떻게 쉽게 구하는가?
      1. idx = 43으로 두고, idx &= idx – 1 연산을 idx가 0이 될 때까지 수행한다.
      2. 이게 왜 되는지 이해가 안 된다면 idx와 idx - 1을 이진법으로 나타내고, and 연산을 수행해보면 이해가 될 것이라 장담한다.
      3. 사실 LSB 자체를 구하는 것은 업데이트 연산에서 볼 수 있듯이 (idx & -idx)로 구할 수 있다. 하지만 LSB를 빼는 것은 idx &= idx - 1로도 가능하다.
  3. 위와 같이 이진법으로 접근해보면, 시간복잡도가 $O(log N)$인 것을 알 수 있다.

값 업데이트($O(log N)$)

arr[7]을 업데이트했다고 가정해보자. 좀 전에 봤던 그림을 다시 가져왔다.

04_FenwickTree3

arr[7]을 업데이트했다면, data[i]는 arr[j]들의 합으로 이루어져 있고, 그 값을 프로그램이 끝날 때까지 유지해야 한다. 그러면 arr[7]이 계산식에 포함되어 있는 모든 data[i]들을 업데이트해야 한다.

그럼 문제는 다음으로 연결된다.

arr[7]을 계산식에 포함하는 data[i]들은 어떤 것이 있는가?

일단 답을 보자. data[7], data[8], data[16]이 있다. (N=16) 이는 위 그림에서 7 위쪽으로 화살표를 쭉 그려보면 알 수 있다. data[7]은 당연히 업데이트해야 하고, 화살표와 만나는 data[8]과 data[16]을 업데이트해야 한다.

각 숫자들을 이진법으로 나타내보자. $00111_2, 01000_2, 10000_2$이다. 규칙성이 보이는가? 조금은 어려울 것이다. 답은, LSB를 더하면 다음 수가 된다는 것이다.

다른 예를 들어보겠다. arr[3]을 업데이트하면, data[3], data[4], data[8], data[16]을 업데이트한다.

  1. $3 = 00011_2$
  2. $4 = 00011_2 + 00001_2 = 00100_2$
  3. $8 = 00100_2 + 00100_2 = 01000_2$
  4. $16 = 01000_2 + 01000_2 = 10000_2$

조금 전에 구간 합을 구할 때는 LSB를 빼 주었다. 업데이트를 할 때는 LSB를 더해 준다. 이것이 가능한 이유는 역시 손으로 몇 개 정도 그려 보면 이해할 수 있다.

구현

코드의 가독성을 위해 그리고 N이 작을 때 메모리를 아끼기 위해 동적으로 data를 vector<int>로 선언하여 FenwickTree class 안에 넣었다.

  • 하지만, 실제 PS 문제를 풀 때는 그냥 $2^n + 1$ 크기만큼 배열을 전역 변수로 설정해버리는 것이 실행 시간이 더 빠르다.
  • arr[i] = sum[i] - sum[i-1]임을 이용하면 arr배열을 유지할 필요가 없다.
  • 사실 이 클래스의 경우 long long을 많이 사용하기 때문에 template을 사용하는 이유가 별로 없긴 하다.
#include "sharifa_header.h"

template <typename T>
class FenwickTree {
public:
    int size;
    vector<T> arr;
    vector<ll> data;

    FenwickTree<T>(int _N) {
        size = _N;
        arr.resize(size + 1);
        data.resize(size + 1);
    }

    void update(int x, T val) {
        T delta_val = val - arr[x];
        arr[x] = val;

        while (x <= size) {
            data[x] += delta_val;
            x += (x&-x);
        }
    }
    ll sum(int x) {
        ll ret = 0;
        while (x) {
            ret += data[x];
            x &= x - 1;
        }
        return ret;
    }
    ll sum(int x, int y) {
        return sum(y) - sum(x - 1);
    }
};

2차원 펜윅 트리 구현

이는 별다른 처리 해 줄 필요 없이 단순히 차원 확장을 한 것에 불과하다. 배열이 2차원이 되고, while문이 두 개가 되었을 뿐이다.

#include "sharifa_header.h"

class FenwickTree2D {
public:
    int size;
    vector<vector<long long> > data;

    FenwickTree2D(int _N) {
        size = _N;
        data = vector<vector<long long> >(size + 1, vector<long long>(size + 1));
    }

    void update(int x, int y, int val) {
        ll dval = val - sum(x, y, x, y);
        int yy;
        while (x <= size) {
            yy = y;
            while (yy <= size) {
                data[x][yy] += dval;
                yy += yy & -yy;
            }
            x += x & -x;
        }
    }
    ll sum(int x, int y) {
        ll ret = 0;
        int yy;
        while (x) {
            yy = y;
            while (yy) {
                ret += data[x][yy];
                yy -= yy & -yy;
            }
            x -= (x&-x);
        }
        return ret;
    }
    inline ll sum(int x1, int y1, int x2, int y2) {
        return sum(x2, y2) - sum(x1 - 1, y2) - sum(x2, y1 - 1) + sum(x1 - 1, y1 - 1);
    }
};

문제 풀이

BOJ 02042(구간 합 구하기)

문제: 구간 합 구하기

풀이: BOJ 02042(구간 합 구하기) 문제 풀이

BOJ 11658(구간 합 구하기 3)

문제: 구간 합 구하기 3

풀이: BOJ 11658(구간 합 구하기 3) 문제 풀이

BOJ 01280(나무 심기)

문제: 나무 심기

풀이: BOJ 01280(나무 심기) 문제 풀이

Related Posts