Gorio Tech Blog search

디닉 알고리즘(Dinic's Algorithm)

11 Jul 2018 | Dinic Network Flow Maximum Flow

목차

참조

분류 URL
문제 최대 유량
응용 문제 스포일러 1
참조 라이브러리 sharifa_header.h, bit_library.h
이 글에서 설명하는 라이브러리 dinic.h

그림 출처: wikipedia

개요

시간복잡도: $ O(V^2 \cdot E) $

공간복잡도: $ O(V^2) $ 또는 $ O(V+E) $

  • V는 정점(vectex)의 수, E는 간선(edge)의 수이다.

이 글에서는 네트워크 플로우(Network Flow) 분야에서 Maximum Flow를 구하는 알고리즘인 디닉 알고리즘에 대해서 설명한다.

Maximum Flow를 구하는 다른 대표적인 알고리즘으로 에드몬드-카프 알고리즘(Edmonds–Karp algorithm), 포드-풀커슨 알고리즘(Ford–Fulkerson algorithm)이 있지만, 현재 PS에서 구현할 만한 알고리즘 중 가장 빠른 알고리즘은 디닉 알고리즘이다. 그래서 여러 개 외울 필요 없이 알고리즘 하나만 알아두는 것이 좋을 듯 하다.

Network Flow(네트워크 플로우)

네트워크 플로우에 대한 기본적인 설명을 조금 적어 두려고 한다. 예를 하나 들면, Network Flow는 파이프가 복잡하게 연결되어 있고, 각 파이프는 물이 흐를 수 있는 최대 양이 정해져 있고, source에서 sink방향으로 물이 흐를 때, 물이 흐를 수 있는 최대 양을 구하는 것이라고 보면 된다.

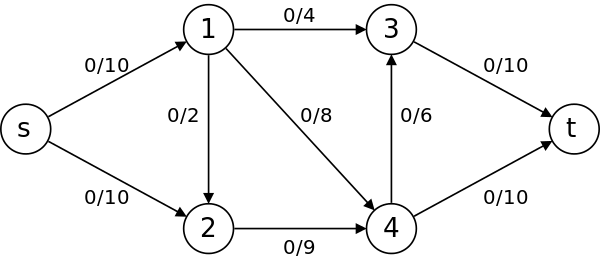
01_network_flow

  • s는 source를 의미한다. 물이 나오는 원천이라고 생각하면 된다.
  • t는 sink를 의미한다. 물이 최종적으로 들어가는 곳이라 생각하면 된다. 모든 물(유량)은 source에서 sink로 흐른다.
  • 두 정점을 잇는 간선은 해당 정점 사이에 흐를 수 있는 최대 물(유량)을 의미한다. s에서 1번 정점으로 0/10이라고 적혀 있는데, 여기서 10이 최대 유량이다.
  • 잔여유량은 최대유량에서 현재 유량을 뺀 값이다. s에서 1번 정점으로 0/10인 것은 현재 유량이 0이고 따라서 잔여유량은 10이다.

네트워크 플로우의 Maximum Flow는 Minimum Cut과 깊은 연관이 있다.

알고리즘

디닉 알고리즘은 크게 두 단계로 이루어진다.

  1. BFS를 써서 레벨 그래프(Level Graph)를 생성하는 것
  2. DFS를 써서, 레벨 그래프에 기초한 차단 유량(Blocking Flow)의 규칙을 지키면서, 최대 유량을 흘려주는 것

레벨 그래프(Level Graph)

레벨 그래프는 각 정점들에 source로부터의 최단 거리를 레벨 값을 할당한 그래프이다. 아래 그림에서 source의 레벨은 0이되고 source와 인접한 1번과 2번 정점의 레벨은 1, 이후는 2… 등이 된다. 빨간색 숫자로 적혀 있는 것이 레벨이다.

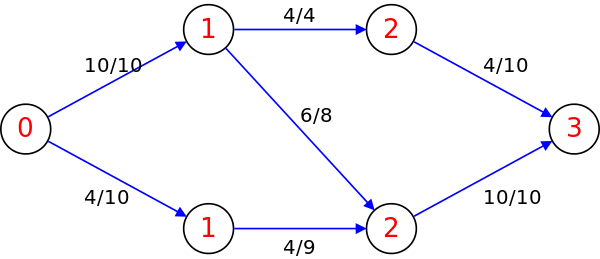
02_residual_capacity

레벨 그래프는 BFS로 구현한다.

차단 유량(Blocking Flow)

디닉 알고리즘에서는, 유량을 흘려보낼 때 레벨 차이가 딱 1이 나는 정점으로만 유량을 보낼 수 있다. 즉 바로 위의 그림에서의 간선과 같은 곳으로만 보낼 수 있다. 레벨이 같아도 안 된다.

유량을 흘려보내는 것은 DFS로 구현한다. source에서 시작하여, 차단 유량 규칙을 만족하는 정점으로만 따라가면서 최종적으로 sink에 도달할 때까지 탐색하는 과정을 반복한다.

위의 레벨 그래프에서는 다음 세 경로를 DFS로 찾을 수 있다.

(s, 1, 3, 4): 유량 4
(s, 1, 4, t): 유량 6
(s, 2, 4, t): 유량 4

반복

BFS 1번 그리고 DFS를 한번씩 해서는 최대 유량이 찾아지지 않는다. 다만 복잡한 것은 아니고, 위의 과정을 반복해주면 된다.

다시 BFS를 돌려 레벨 그래프를 새로 생성한다.

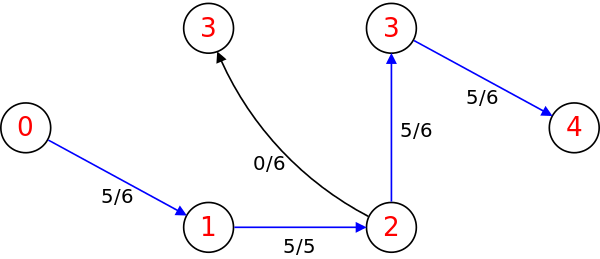
03_residual_capacity

위의 레벨 그래프에서는 다음 경로를 DFS로 찾을 수 있다.

(s, 2, 4, 3, t): 유량 5

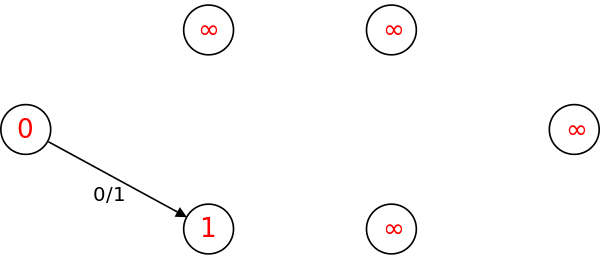
다시 레벨 그래프를 그리면, 더 이상 sink로 가는 경로가 없음(sink의 레벨이 $\inf$)을 알 수 있다. 알고리즘을 종료한다.

04_residual_capacity

구현

BFS는 어려운 부분이 아니기 때문에 설명은 생략하도록 하겠다.

DFS의 구현은 조금 까다롭다.

  1. 우선 sink(T)에 도달하면 종료한다.
  2. 종료할 때 max_flow라는 것을 리턴한다. 이는 Network Flow에서 수송량은 경로에 포함된 파이프 최대 유량의 최솟값이기 때문이다. flow의 계산식을 잘 보면 최대 유량과 min 연산을 취하는 것을 볼 수 있다.
  3. 레벨 차이가 1 나는지를 먼저 검사한다. 그리고 그 정점의 잔여 용량이 0보다 큰지 또한 검사한다.
  4. 만약 그런 정점을 찾았으면, 재귀적으로 DFS를 수행한다.
  5. DFS가 리턴되어 반환한 flow 값이 0보다 크면, 아직 DFS로 탐색할 수 있는 경로가 남아 있다는 뜻이다.
  6. 경로를 찾았으므로, 해당 경로를 따라서(스택에 재귀 호출로 쌓인 함수에 의해 자동으로 역추적됨) 잔여 용량을 줄여준다.
  7. 만약 어떤 flow도 0이라면, 경로를 찾지 못한 것이므로 종료한다.
  8. next_v라는 배열(벡터)이 있다. 이는 DFS에서 다음 경로를 효율적으로 찾기 위해 존재하는 배열이다.
    1. DFS로 경로를 탐색할 떄 정점 번호가 낮은 정점부터 탐색한다.
    2. 만약 처음에 1번 정점으로 가는 경로를 모두 찾았다면, 더 이상 1번 정점으로는 갈 필요가 없다. 이때 next_v[u]를 1 증가시켜, 다음부터는 2번 정점부터 탐색을 시작하도록 한다.
    3. 2번도 끝났으면 또 next_v[u]를 증가시킨다. 이를 반복한다.
    4. 코드 상으로는 int &i로 되어 있다. i가 레퍼런스로 선언되어 있기 때문에 for loop의 i++ 구문에 따라 같이 증가한다(i는 next_v[u]와 값을 공유한다)
    int dfs(int u, int max_flow) {
        if (u == T)
            return max_flow;

        for (int &i = next_v[u]; i < edges[u].size(); i++) {
            int v = edges[u][i].v, cap = edges[u][i].cap;

            if (level[u] + 1 == level[v] && cap > 0) {
                int flow = dfs(v, min(max_flow, cap));

                if (flow > 0) {
                    edges[u][i].cap -= flow;
                    edges[v][edges[u][i].ref].cap += flow;
                    return flow;
                }
            }
        }
        return 0;
    }

addEdge 함수의 inv는 각 간선이 양방향 수송이 가능하면 true로 지정하면 된다. sparse graph일 경우를 대비해 edges를 2차원 배열로 표현하지 않고 대신 역방향 간선에 대한 참조를 저장하고 있다. 이러면 정점이 많을 경우에도 메모리 사용량을 줄일 수 있다.

구현은 다음과 같다.

#pragma once

#include "sharifa_header.h"

struct Edge {   // u -> v
    int v, cap, ref;
    Edge(int v, int cap, int ref) :v(v), cap(cap), ref(ref) {}
};

class Dinic {
    int S, T;
    vector<vector<Edge> > edges;    // graph
    // level: 레벨 그래프, next_v: DFS에서 flow 계산 시 역추적에 사용
    vector<int> level, next_v;

public:
    Dinic(int MAX_V, int S, int T):S(S), T(T) {
        edges.resize(MAX_V);
        level.resize(MAX_V);
        next_v.resize(MAX_V);
    }

    void addEdge(int u, int v, int cap, bool inv) {
        edges[u].emplace_back(v, cap, (int)edges[v].size());
        edges[v].emplace_back(u, inv ? cap : 0, (int)edges[u].size() - 1);
    }

    bool bfs() {
        fill(level.begin(), level.end(), -1);

        queue<int> q;
        level[S] = 0;
        q.push(S);

        while (!q.empty()) {
            int u = q.front();   q.pop();
            for (auto edge : edges[u]) {
                int v = edge.v, cap = edge.cap;

                if (level[v] == -1 && cap > 0) {
                    level[v] = level[u] + 1;
                    q.push(v);
                }
            }
        }
        return level[T] != -1;
    }

    void reset_next_v() {
        fill(next_v.begin(), next_v.end(), 0);
    }

    int dfs(int u, int max_flow) {
        if (u == T)
            return max_flow;

        for (int &i = next_v[u]; i < edges[u].size(); i++) {
            int v = edges[u][i].v, cap = edges[u][i].cap;

            if (level[u] + 1 == level[v] && cap > 0) {
                int flow = dfs(v, min(max_flow, cap));

                if (flow > 0) {
                    edges[u][i].cap -= flow;
                    edges[v][edges[u][i].ref].cap += flow;
                    return flow;
                }
            }
        }
        return 0;
    }
};

문제 풀이

BOJ 06086(최대 유량)

문제: 최대 유량

풀이: BOJ 06086(최대 유량) 문제 풀이

스포일러 문제

문제: 스포일러 문제

풀이: 스포일러 풀이

Related Posts