Gaussian Process 설명

목차

• 1. Basics of Gaussian Process
• 2. Gaussian Process in Machine Learning
  • 2.1. Posterior Gaussian Process
  • 2.2. Training a Gaussian Process
  • 2.3. Conclusions and Future Directions
• 3. Gaussian Process Regression
  • 3.1. Overview
  • 3.2. Definition of Gaussian Process
  • 3.3. How to Regress using Gaussian Process
  • 3.4. GPR in the Real World
• 4. Fitting Gaussian Process with Python
• Reference

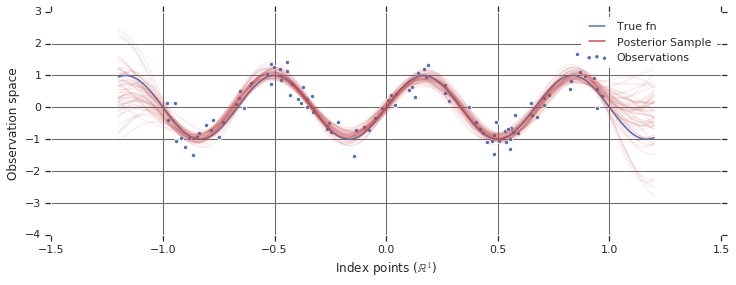
Gaussian Process에 대해 알아보자!

Gaussian Process는 Random(Stochastic) Process의 한 예이다. 이 때 Random Process는 시간이나 공간으로 인덱싱된 Random Variable의 집합을 의미한다. GP의 정의는 아래와 같다.

Stochastic process such that every finite collection of those random variables has a multivariate normal distribution.

이는 또한 이 Random Variable들의 선형 결합 일변량 정규분포를 따른다는 말과 동일한 설명이고, GP의 일부를 가져와도 이는 항상 다변량 정규분포를 따른다는 것을 의미한다. 또한 다변량 정규분포는 주변 분포와 조건부 분포 역시 모두 정규분포를 따르기 때문에 이를 계산하기 매우 편리하다는 장점을 지닌다.

GP는 일종의 Bayesian Non-parametric method으로 설명되는데, 이 때 Non-parametric이라는 것은 parameter의 부재를 의미하는 것이 아니라 parameter가 무한정 (infinite) 있다는 것을 의미한다.

지금부터는 GP에 대해 이해하기 위해 단계적으로 설명을 진행할 것이다.

1. Basics of Gaussian Process

다변량 정규분포를 생각해보자.

앞서 언급하였듯이 이 다변량 정규분포를 이루는 확률변수의 어떠한 부분집합에 대해서도 주변 분포와 조건부 분포 모두 정규분포를 따른다. GP는 여기서 한발 더 나아가서, 이러한 다변량 정규분포를 무한 차원으로 확장시키는 개념으로 생각하면 된다.

이 무한의 벡터를 일종의 함수로 생각할 수도 있을 것이다. 연속형 값을 인풋으로 받아들이는 함수를 가정하면, 이는 본질적으로 input에 의해 인덱싱된 값들을 반환하는 무한한 벡터로 생각할 수 있다. 이 아이디어를 무한 차원의 정규분포에 적용하면 이것이 바로 GP의 개념이 된다.

따라서 Gaussian Process는 함수에 대한 분포라고 표현할 수 있다. 다변량 정규분포가 평균 벡터와 공분산 행렬로 표현되는 것처럼, GP 또한 평균 함수와 공분산 함수를 통해 다음과 같이 정의된다.

GP에 있어서 Marginalization Property는 매우 중요한 특성이다. 우리가 관심 없거나 관측되지 않은 수많은 변수에 대해 Marginalize할 수 있다.

GP의 구체적 예시를 다음과 같이 들 수 있을 것이다. 실제로 이는 가장 흔한 설정이다.

여기서 공분산 함수로 Squared Exponential을 사용하였는데, $x$와 $x\prime$이 유사한 값을 가질 수록 1에 수렴하는 함수이다. (거리가 멀수록 0에 가까워짐) 평균 함수로는 0을 사용하였는데, 사실 평균 함수로 얻을 수 있는 정보는 별로 없기에 단순한 설정을 하는 것이 가장 편리하다.

유한한 데이터 포인트에 대해 GP는 위에서 설정한 평균과 공분산을 가진 다변량 정규분포가 된다.

다음 Chapter부터는 본격적으로 이론에 대한 부분을 정리하도록 하겠다. 2개의 논문을 정리하였는데, 첫 번째 논문은 Gaussian Process의 가장 기본적이고 중요한 내용을 담은 논문이며, 두 번째 논문은 좀 더 개념을 확장하고 직관적으로 Gaussian Process Regression에 대해 서술한 논문이다.

2. Gaussian Process in Machine Learning

본 논문은 GP가 회귀를 위한 Bayesian 프레임워크를 형성하기 위해 어떻게 사용되는지, Random(Stochastic) Process가 무엇이고 이것이 어떻게 지도학습에 사용되는지를 설명하는 것이 주 목적이다. 또한 공분산 함수의 Hyperparameter 설정에 관한 부분, 그리고 주변 우도와 Automatic Occam’s Razor에 관한 이야기도 포함한다.

(Occam’s Razor: 오캄의 면도날 원칙, 단순함이 최고다.)

2.1. Posterior Gaussian Process

GP는 함수에 대한 분포로 정의되며, 이러한 GP는 베이지안 추론의 Prior로 사용된다. 이 Prior는 학습 데이터에 의존하지 않으며 함수들에 대한 어떤 특성을 구체화한다. Posterior Gaussian Process의 목적은 학습데이터가 주어졌을 때, 이 Prior를 업데이트하는 방법을 도출해내는 것이다. 나아가 새로운 데이터가 주어졌을 때 적절히 예측 값을 반환하는 것이 목표가 될 것이다.

기존의 학습데이터와 새로운 테스트 데이터를 분리하여 다음과 같은 결합 분포를 상정해보자.

이제 우리가 알고 싶어하는 f*의 조건부 분포는 아래와 같은 형상을 지녔다. 아래 식은 테스트 데이터에 대한 사후분포에 해당한다.

이와 같은 분포를 얻을 수 있는 이유는 결합 정규분포를 조건화하는 공식인 다음의 결과에 기인한다.

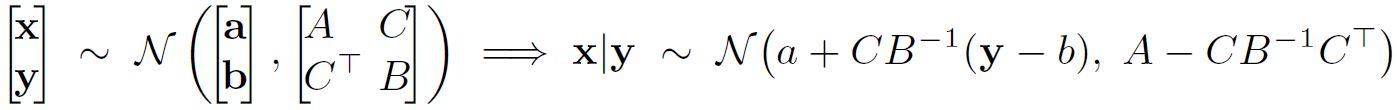
위에서 확인한 사후분포에 기반하여 Posterior Process를 구해보면 아래와 같다.

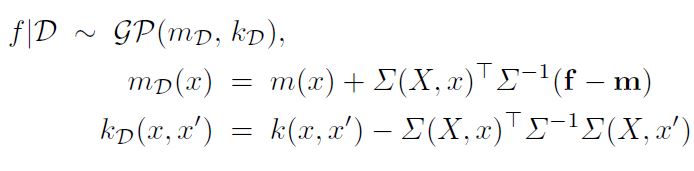
이 때 $\Sigma(X, x)$ 는 모든 학습 데이터와 $x$ 의 공분산 벡터를 의미한다. 이제 위 식을 자세히 뜯어보자. Posterior Process의 공분산 함수는 Prior의 공분산 함수에서 양의 값을 뺀 것과 같다. 즉 Posterior Process의 공분산 함수는 Prior의 그것보다 언제나 작은 값을 가진다는 의미이다. 이것은 논리적인데, 데이터가 우리에게 정보를 제공하였기 때문에 Posterior의 분산이 감소하는 것이다.

자 이제 학습 데이터의 Noise를 고려해야 한다. 이에 대해서 정규 분포를 설정하는 것이 일반적이다. Noise를 고려한 후 다시 정리하면 아래와 같다.

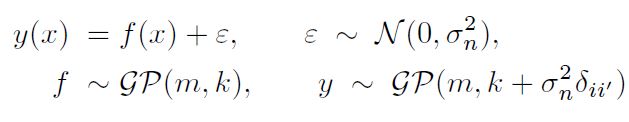
이제 Posterior Process에서 샘플링을 진행할 수 있다. 이렇게 평균 함수와 공분산 함수를 정의함으로써 학습 데이터가 주어졌을 때 Prior를 Posterior로 업데이트할 수 있게 되었다. 그러나 문제가 찾아왔다. 어떻게 평균 함수와 공분산 함수를 적절히 설정하는가? 그리고 Noise Level( $\sigma_n^2$ )은 어떻게 추정하는가?

2.2. Training a Gaussian Process

사실 일반적인 머신러닝 적용 케이스에서 Prior에 대해 충분한 정보를 갖고 있는 것은 드문 경우이다. 즉, 평균 함수와 공분산 함수를 정의하기에는 갖고 있는 정보가 부족하다는 것이다. 우리는 갖고 있는 학습 데이터에 기반하여 평균, 공분산 함수에 대해 적절한 추론을 행해야 한다.

Hyperparameter에 의해 모수화되는 평균, 공분산 함수를 가진 Hierarchical Prior를 사용해보자.

이제 우리는 $\theta=[a, b, c, \sigma_y, \sigma_n, l]$ 이라는 Hyperparameter 집합을 설정하였다. 이러한 계층적 구체화 방법은 vague한 Prior 정보를 간단히 구체화할 수 있게 해준다.

우리는 데이터가 주어졌을 때 이러한 모든 Hyperparameter에 대해 추론을 행하고 싶다. 이를 위해서는 Hyperparameter가 주어졌을 때 데이터의 확률을 계산해야 한다. 이는 어렵지 않다. 주어진 데이터의 분포는 정규 분포임을 가정했기 때문이다. 이제 Log Marginal Likelihood를 구해보자.

이제 편미분 값을 통해 이 주변 우도를 최적화(여기서는 최소화)하는 Hyperparameter의 값을 찾을 수 있다. 아래에서 $\theta_m$ 와 $\theta_k$ 는 평균과 공분산에 관한 Hyperparameter를 나타내기 위한 parameter이다.

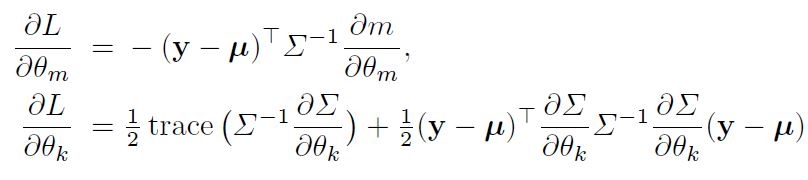
위 값들은 Conjugate Gradients와 같은 Numerical Optimization에 사용된다.

GP는 Non-parametric 모델이기 때문에 Marginal Likelihood의 형상은 Parametric 모델에서 보던 것과는 사뭇 다르다. 사실 만약 우리가 Noise Level인 $\sigma_n^2$ 를 0으로 설정한다면, 모델은 정확히 학습 데이터 포인트와 일치하는 평균 예측 함수를 생성할 것이다. 하지만 이것은 주변 우도를 최적화하는 일반적인 방법이 아니다.

Log Marginal Likelihood 식은 3가지 항으로 구성되어 있는데, 첫 번째는 Complexity Penalty Term으로 모델의 복잡성을 측정하고 이에 대해 페널티를 부과한다. Negative Quadratic인 두 번째 항은 데이터에 적합하는 역할을 수행하며, 오직 이 항만이 학습 데이터의 Output인 $\mathbf{y}$ 에 의존적이다. 세 번째 항은 Log-Normalization Term으로 데이터에 대하여 독립적이며 사실 뭐 그리 중요한 항은 아니다.

GP에서 페널티와 데이터에 대한 적합의 trade-off는 자동적이다. 왜냐하면 Cross Validation과 같은 외부적 방법이 세팅될 Parameter가 존재하지 않기 때문이다. 실제로 이와 같은 특성은 보통의 머신러닝 알고리즘 상에 존재하는 Hyperparameter 튜닝에 소요되는 시간을 절약하게 해주기 때문에 학습을 더욱 간단하게 만드는 장점을 갖게 된다.

2.3. Conclusions and Future Directions

본 논문에서는 GP가 굉장히 변동성이 크고 유연한 비선형적 회귀를 구체화하는 데 편리하게 사용되는 과정에 대해 알아보았다. 본 논문에서는 오직 1가지 종류의 공분산 함수가 사용되었지만, 다른 많은 함수들이 사용될 수 있다. 또한 본 논문에서는 오직 가장 간단한 형태인 정규 분포의 Noise를 가정하였지만, 그렇지 않을 경우 학습은 더욱 복잡해지고 Laplace 근사와 같은 방법이 도입되거나 Sampling이 이루어져야만 non-Gaussian Posterior를 정규분포와 유사하게 만들 수 있다.

또 중요한 문제점은 계산 복잡성이다. 공분산 행렬의 역행렬을 구하기 위해서는 메모리 상에서는 $\mathcal{O}(n^2$ 의 복잡도가, 계산 상에서는 $\mathcal{O}(n^3)$ 의 복잡도가 발생한다. 리소스에 따라 다르지만, 행이 10,000개만 넘어가도 직접적으로 역행렬을 계산하기에는 많은 무리가 따른다. 따라서 근사적인 방법이 요구되는데, 본 논문이 나온 시점이 2006년임을 고려하면, 이후에도 많은 연구가 진행되었음을 짐작할 수 있을 것이다.

한 예로 이 논문이 있는데, 추후에 다루도록 할 것이다.

3. Gaussian Process Regression

본 Chapter에서는 두 번째 논문을 기반으로 좀 더 단계적으로 설명을 해볼 것이다.

논문의 내용을 설명하기 전에 전체적인 구조를 다시 한번 되짚어보도록 하자.

3.1. Overview

비선형 회귀 문제를 생각해보자. 우리는 데이터가 주어졌을 때 이를 표현하는 어떤 함수 f를 학습하고 싶고 이 함수는 확률 모델이기 때문에 신뢰 구간 또는 Error Bar를 갖게 된다.

Gaussian Process는 평균 함수와 공분산 함수를 통해 이 함수에 대해 분포를 정의한다. 이 함수는 Input Space $\mathcal{X}$ 를 $\mathcal{R}$ 로 mapping하며, 만약 두 공간이 정확히 일치할 경우 이 함수는 infinite dimensional quantity가 된다.

그리고 베이즈 정리에 따라 위 확률은 Bayesian Regression에 사용된다.

Posterior를 구하기 위해서는 당연히 Prior와 Likelihood가 필요한데, 이 때 Prior는 Gaussian Process를 따른다고 가정한다. 이제 Likelihood를 구해야 한다.

우리가 수집한 데이터 $\mathcal{D}$ 는 일반적으로 Noise를 포함하고 있다. 따라서 우리의 정확한 목표는 $f(x)$ 를 추정하는 것이 아니라 Noise를 포함한 $y$ 를 추정하는 것이어야 한다. 평균 함수를 0으로 가정하고 $y$ 를 비롯하여 GPR에 필요한 모델들에 대해 정리해보자.

다음 Chapter에서도 나오겠지만 이 Noise의 분산을 공분산 함수 속으로 집어넣을 수 있다. (자세한 수식은 다음 Chapter를 참조하라) 그러면 사실 아래의 $K$ 는 $K + \sigma_n^2$ 를 의미하게 된다.

f의 Prior는 GP고, Likelihood는 정규분포이므로 f에 대한 Posterior 또한 GP이다. 일단 주어진 데이터에 기반하여 Marginal Likelihood를 구해보자.

그런데 이 때 이전 Chapter와 마찬가지로 공분산 함수를 정의할 때 사용되는 Hyperparameter로 $\theta$ 를 정의하게 되면, Marginal Likelihood는 정확히 아래와 같이 표현할 수 있다.

이 식에 Log를 취해서 다시 정리하면 Log Marginal Likelihood가 된다. ( $\theta$ subscript는 생략한다.)

Numeric한 방법으로 위 목적 함수를 최적화(최소화)하는 $\theta$ 를 구하면 이는 공분산 함수의 최적 Hyperparameter가 된다. 이제 예측을 위한 분포를 확인해보자. 새로운 데이터 포인트 $x_*$ 가 주어졌을 때의 예측 값에 관한 사후분포이다.

이제 위 분포를 바탕으로 Sampling을 진행하고, 평균과 분산을 바탕으로 그래프를 그리면 본 글의 가장 서두에서 본 것과 같은 아름다운 그래프를 볼 수 있다.

평균인 $K_*K^{-1}\mathbf{y}$ 는 다음과 같이 $\mathbf{y}$ 에 대한 선형결합으로 표현할 수도 있다.

지금까지 설명한 내용이 바로 Gaussian Process를 Function Space View로 이해한 것이다.

3.2. Definition of Gaussian Process

지금부터는 논문의 내용을 정리한 것이다. 사실 GP의 기본적인 설명은 끝났다고 봐도 무방하지만, 그럼에도 이 세심한 논문의 설명을 다시 한 번 읽어보지 않을 수가 없다. 정의에 대한 부분은 처음에 설명하였으므로 생략하도록 하겠다.

Chapter1에서 공분산 함수 $ k(x, x\prime) $에 대해서 설명하였는데, 본 논문에 맞추어 Notation을 살짝 변형하도록 하겠다. (이전 Chapter에서는 이 공분산 함수를 가장 단순한 버전인 $\Sigma$ 로 표현하였다.)

정말 기호만 살짝 바뀌었다. $x$가 $x\prime$과 유사할 수록 $f(x)$라 $f(x\prime)$과 상관성(Correlation)을 가진다고 해석할 수 있다. 이것은 좋은 의미이다. 왜냐하면 함수가 smooth해지고 이웃한 데이터 포인트끼리 더욱 유사해지기 때문이다.

만약 그 반대의 경우 2개의 데이터 포인트는 서로 마주칠 수도 없다. 즉 새로운 $x$값이 삽입될 때, 이와 먼 곳에 있는 관측값들은 그다지 큰 영향을 미칠 수 없다. 이러한 분리가 갖는 효과는 사실 length parameter인 $l$에 달렸있는데, 이 때문에 이 공분산 함수는 상당한 유연성을 지니는 식이 된다.

하지만 데이터는 일반적으로 Noise를 포함하고 있다. 이 때문에 언제나 측정 오차는 발생하기 마련이다. 따라서 $y$ 관측값은 $f(x)$에 더불어 Gaussian Noise를 포함하고 있다고 가정하는 것이 옳다.

많이 보았던 회귀식 같아 보인다. 이 Noise를 공분산 함수안에 집어넣으면 아래와 같은 형식을 갖추게 된다.

여기서 $\delta(x, x\prime)$은 Kronecker Delta Function이다.

많은 이들은 GP를 사용할 때 $\sigma_n$을 공분산 함수와 분리해서 생각하지만 사실 우리의 목적은 y* 를 예측하는 것이지 정확한 f* 를 예측하는 것이 아니기 때문에 위와 같이 설정하는 것이 맞다.

Gaussian Process Regression을 준비하기 위해 모든 존재하는 데이터포인트에 대해 아래와 같은 공분한 함수를 계산하도록 하자.

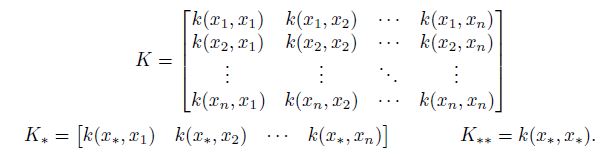
$K$의 대각 원소는 $\sigma_f^2 + \sigma_n^2$ 이고, 비대각 원소 중 끝에 있는 원소들은 $x$ 가 충분히 큰 domain을 span할수록 0에 가까운 값을 갖게 된다.

3.3. How to Regress using Gaussian Process

GP에서 가장 중요한 가정은 우리의 데이터가 다변량 정규 분포로부터 추출된 Sample로 표현된다는 것이므로 아래와 같이 표현할 수 있다.

우리는 물론 조건부 확률에 대해 알고 싶다.

이 확률은 데이터가 주어졌을 때 $y_*$ 에 대한 예측의 확실한 정도를 의미한다.

정규분포이므로, $y_*$ 에 대한 Best Estimate는 평균이 될 것이다.

그리고 분산 또한 아래와 같다.

이제 본격적으로 예제를 사용해보자. Noise가 존재하는 데이터에서 다음 포인트 $x_*$ 에서의 예측 값은 얼마일까?

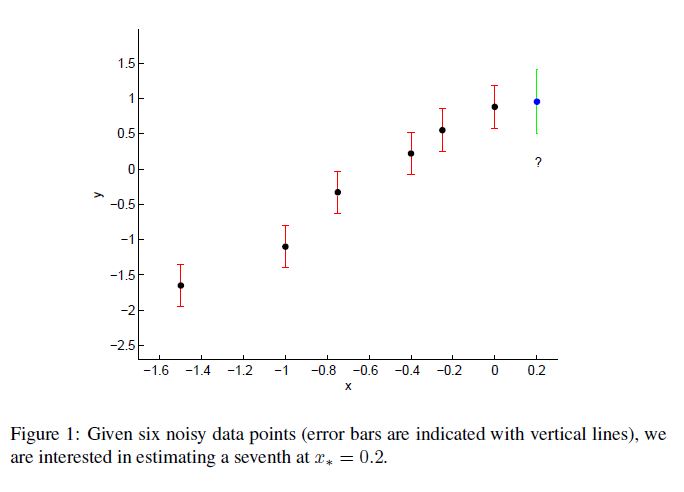
6개의 관측값이 다음과 같이 주어졌다.

x = [-1.5, -1, -0.75, -0.4, -0.25, 0]

Noise의 표준편차 $\sigma_n$ 이 0.3이라고 하자. $\sigma_f$ 와 $l$ 을 적절히 설정하였다면 아래와 같은 행렬 $K$를 얻을 수 있다.

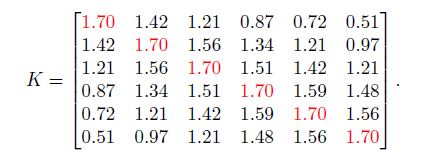
공분산 함수를 통해 아래 사실을 알 수 있다.

그런데 매번 이렇게 귀찮게 구할 필요는 없다. 엄청나게 많은 데이터 포인트가 존재하더라도 이를 한번에 큰 $K_*$ 과 $K_{**}$ 을 통해 계산해버리면 그만이다.

만약 1000개의 Test Point가 존재한다면 $K_{**}$ 는 (1000, 1000)일 것이다.

95% Confidence Interval은 아래 식으로 구할 수 있고 이를 그래프로 표현하면 아래 그림과 같다.

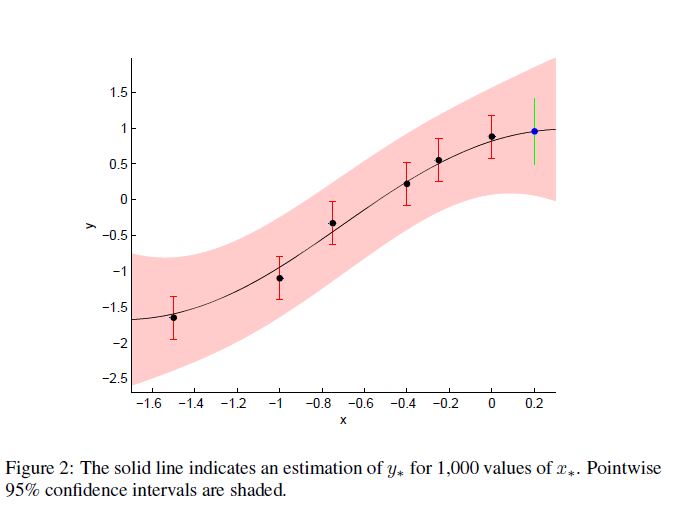
3.4. GPR in the Real World

이전 Chapter에서 보았던 내용이 신뢰를 얻기 위해서는 사실 우리가 얼마나 공분산 함수를 잘 선택하느냐에 달려있다. $\theta = [l, \sigma_f, \sigma_n]$ 라는 Parameter 집합이 적절히 설정되어야만 결과가 합리적일 것이다.

$\theta$ 의 Maximum a Posteriori Estimate는 다음 식이 최댓값을 가질 때 찾을 수 있다.

베이즈 정리에 따라 우리가 $\theta$ 에 대해 거의 아는 것이 없다고 가정할 때 우리는 다음과 같은 식을 최대화해야 한다.

다변량 최적화 알고리즘(예: Conjugate Gradients, Nelder-Mead simplex)을 이용하면 예를 들어 $l=1, \sigma_f=1.27$ 과 같은 좋은 값을 얻을 수 있다.

그런데 이건 그냥 단지 좋은 값 에 불과하다. 수많은 옵션 중에 딱 하나 좋은 답이 있으면 안되는가? 이 질문에 대한 답은 다음 장에서 찾을 수 있다.

좀 더 복잡한 문제에 대해 생각해보자. 아래와 같은 Trend를 갖는 데이터가 있다고 하자.

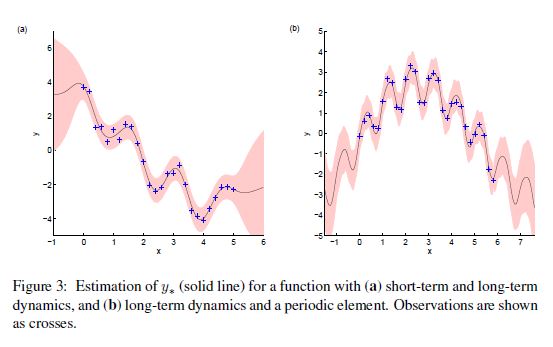
좀 더 복잡한 공분한 함수가 필요할 것 같다.

위 식의 우항에서 첫 번째 부분은 예측변수의 작은 변동을 잡아내기 위함이고, 두 번째 부분은 좀 더 긴 기간 동안의 변동성을 포착하기 위해 설계되었다. ( $l_2 \approx 6l_1$ )

이 공분산 함수는 $K$ 가 positive definite이기만 하면 복잡한 데이터에 적합하게 무한대로 확장할 수 있다.

그런데 이 함수가 정말 시간적 흐름을 포착할 수 있을까? 보완을 위해 새로운 항을 추가해보자.

우항의 첫 부분은 마찬가지로 장기간의 트렌드를 포착하기 위해 설계된 부분이고, 두 번째 부분은 빈도를 나타내는 $\nu$ 와 함께 periodicity를 반영하게 된다. 위에서 살펴본 그림의 검은 실선이 위 공분산 함수를 이용하여 적합한 것이다.

4. Fitting Gaussian Process with Python

베이지안 방법론을 위한 대표적인 라이브러리로 PyMC3가 있지만 본 글에서는 scikit-learn 라이브러리를 이용하겠다.

회귀 문제에서는 공분산 함수(kernel)를 명시함으로써 GaussianProcessRegressor를 사용할 수 있다. 이 때 적합은 주변 우도의 로그를 취한 값을 최대화하는 과정을 통해 이루어진다. 이 Class는 평균 함수를 명시할 수 없는데, 왜냐하면 평균 함수는 0으로 고정되어 있기 때문이다.

분류 문제에서는 GaussianProcessClassifier를 사용할 수 있을 것이다. 언뜻 생각하면 범주형 데이터를 적합하기 위해 정규 분포를 사용하는 것이 이상하다. 이는 Latent Gaussian Response Variable을 사용한 뒤 이를 unit interval(다중 분류에서는 simplex interval)로 변환하는 작업을 통해 해결할 수 있다. 이 알고리즘의 결과는 일반적인 머신러닝 알고리즘에 비해 부드럽고 확률론적인 분류 결과를 반환한다. (이에 대한 자세한 내용은 Reference에 있는 2번째 논문의 7페이지를 참조하길 바란다.)

GP의 Posterior는 정규분포가 아니기 때문에 Solution을 찾기 위해 주변 우도를 최대화하는 것이 아니라 Laplace 근사를 이용한다.

이제부터 아주 간단한 예를 통해 라이브러리를 사용하는 법에 대해 소개하겠다. 본 내용은 scikit-learn 라이브러리 홈페이지에서 확인할 수 있다.

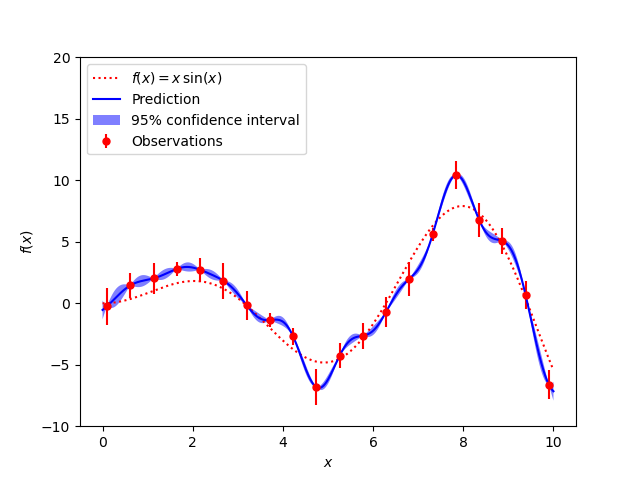
아래와 같은 함수를 추정하는 것이 우리의 목표이다.

import numpy as np

# X, y는 학습 데이터

def f(x):
    """The function to predict."""
    return x * np.sin(x)

X = np.linspace(0.1, 9.9, 20)
X = np.atleast_2d(X).T

# Observations and noise
y = f(X).ravel()
dy = 0.5 + 1.0 * np.random.random(y.shape)
noise = np.random.normal(0, dy)
y += noise

공분산 함수(kernel)를 정의하고 GPR 적합을 시작한다. 본 예시에는 kernel을 구성할 때의 Hyperparameter 최적화에 대한 내용은 포함되어 있지 않다.

from sklearn.gaussian_process import GaussianProcessRegressor
from sklearn.gaussian_process.kernels import WhiteKernel, ConstantKernel as C, RBF

kernel = C(1.0, (1e-3, 1e3)) * RBF(10, (1e-2, 1e2))
gp = GaussianProcessRegressor(kernel=kernel,
                              n_restarts_optimizer=9,
                              optimizer='fmin_l_bfgs_b',
                              random_state=0)
gp.fit(X, y)

아주 드넓은 공간에서 함수 추정을 해보자.

x = np.atleast_2d(np.linspace(0, 10, 1000)).T
y_pred, sigma = gp.predict(x, return_std=True)

plt.figure()
plt.plot(x, f(x), 'r:', label=r'$f(x) = x\,\sin(x)$')
plt.errorbar(X.ravel(), y, dy, fmt='r.', markersize=10, label='Observations')
plt.plot(x, y_pred, 'b-', label='Prediction')
plt.fill(np.concatenate([x, x[::-1]]),
         np.concatenate([y_pred - 1.9600 * sigma,
                        (y_pred + 1.9600 * sigma)[::-1]]),
         alpha=.5, fc='b', ec='None', label='95% confidence interval')
plt.xlabel('$x$')
plt.ylabel('$f(x)$')
plt.ylim(-10, 20)
plt.legend(loc='upper left')
plt.show()

Reference

1) GP 논문1
2) GP 논문2
3) GP 설명 블로그
4) scikit-learn 홈페이지
5) PyMC3 홈페이지