본 글에서는 Graph Neural Networks 이론의 근간 중 하나라고 할 수 있는 Graph Fourier Transform에 대해 설명할 것이다.
Notation의 경우 최대한 가장 자주 쓰이는 형태를 고려하여 작성하였고, 글로써 완전히 전달하는 것이 어렵기 때문에 여러 자료들을 함께 참고하길 바라며, 관련 강의를 들을 수 있다면 더욱 좋을 것이다.

Graph Laplacian

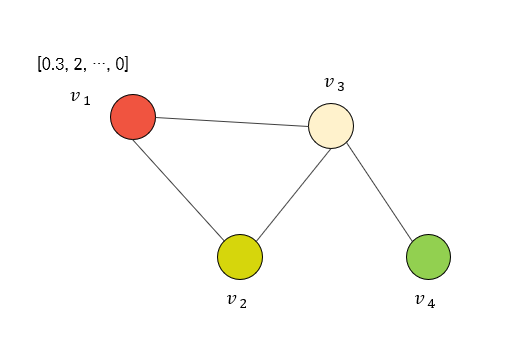
위와 같은 Graph $\mathcal{G}$ 가 존재한다고 할 때, 각 node $v$ 는 feature를 갖고 있다.
각각의 node가 갖고 있는 feature를 그 node의 signal이라고 설정해 볼 때, node $v_1$ 의 signal은 $f_1$ 이라는 함수에 의해 정의된다.

node의 집합 $\mathcal{V}=[v_1, v_2, v_3, v_4]$ 에 대한 node feature matrix는 $(4, d)$ 형태의 2차원 행렬일 것인데,

이 행렬의 각 행이 한 node에 대한 signal이라고 생각해보면 아래와 같이 표현할 수 있다.

[\mathcal{V} \rightarrow \left[\begin{matrix} f_1\f_2\f_3\f_4\ \end{matrix} \right] = \mathbf{f}]

이 Graph의 인접 행렬(Adjacency Matrix)를 표현하면 아래와 같다.

[A = \left[ \begin{matrix} 0 & 1 & 1 & 0
1 & 0 & 1 & 0
0 & 1 & 1 & 1
0 & 0 & 1 & 0
\end{matrix} \right]]

그리고 Graph의 Degree Matrix는 $D$ 이며 이 두 행렬을 이용하여 Laplacian Matrix를 정의한다.

[\mathbf{L} = \mathbf{D} - \mathbf{A}]

Laplacian Matrix를 difference operator로 활용해보자.

위 예시를 적용해보면 아래와 같이 쓸 수 있다.

[h_2 = 2 f_2 - f_1 - f_3]

이를 일반화하여 적어보면 다음과 같다.

[h_i = \Sigma_{j \in N_i} (f_i - f_j)]

이어서 이를 Quadratic Form으로 재표현한 과정은 아래와 같다.

마지막 줄을 보면, 결국 위 식에서 남는 것은 node $i$ 와 $j$ 사이의 연결이 존재할 때, $f_i - f_j$ 의 값이 작으면 연결된 node의 signal이 유사하다는 의미로 생각할 수 있다.

참고로 $\mathbf{D}^{-1} \mathbf{A}$ 혹은 $\mathbf{D}^{-\frac{1}{2}} \mathbf{A} \mathbf{D}^{-\frac{1}{2}}$ 같은 경우는 Transition Matrix라고도 부른다.

Eigen-decomposition of Laplacian Matrix

지난 Chapter에서 정의했던 Laplacian Matrix $\mathbf{L} = \mathbf{D} - \mathbf{A}$ 에 고유값 분해를 적용해보자.

하나의 eigen value에 대해서 다시 살펴보면 아래와 같고, 이 때 $\lambda_i$ 가 클수록 signal $u_i$ 의 frequency가 크다고 해석할 수 있다.

[\mathbf{u}_i^T \mathbf{L} \mathbf{u}_i = \mathbf{u}_i^T \lambda_i \mathbf{u}_i = \lambda_i]

Graph Fourier Transform

푸리에 변환은 다양한 분야에서 활용되는 굉장히 중요한 개념인데, Graph 이론에서도 변형되어 사용된다.
푸리에 변환의 개념을 간단히만 설명하자면, 어떤 입력 signal을 여러 종류의 frequency를 갖는 함수들의 합으로 표현하는 것이라고 볼 수 있다.
자세한 설명은 이 곳을 참조할 것을 권한다.

그러니까 우리는 Graph를 표현하는 어떤 signal이 존재할 때, 이를 우리가 표현할 수 있는 어떤 함수들의 합으로 의미있게 표현하고 싶은 것이다.

핵심부터 말하자면, $\mathbf{L}$ 의 eigen space $\mathcal{F}$ 에 속해있는 $\mathbf{f} \in \mathcal{F}$ 이 존재할 때, 이를 $\hat{\mathbf{f}}$로 변환하는 것을 Graph Fourier Transform라고 한다.

Graph Fourier Mode 혹은 Basis Graph로 $\mathbf{u_i}$ 를 설정하자, 이 벡터는 사실 Graph Laplacian Matrix에서의 orthogonal eigen vector이다.
참고로 $\lambda_i$ 는 frequency, $\hat{f_i}$ 를 Graph Fourier 계수를 의미한다.

Graph Fourier Transform은 아래와 같이 정의한다.

[\hat{\mathbf{f}} = \mathbf{U}^T \mathbf{f} = \Sigma_i f_i \mathbf{u_i}]

[\hat{f_i} = \mathbf{u_i}^T \mathbf{f}]

이 과정은 $\mathbf{f}$ 를 $\mathcal{F}$ 로 projection하는 것을 의미한다. 즉 기존에 존재하던 Graph Signal을 Graph Laplacian Matrix를 통해 새롭게 정의한 eigen space로 투사하는 것이다. 이 과정은 또한 signal을

앞서 설명하였듯이 $\hat{\mathbf{f_i}}$ 는 Graph Fourier Transform의 결과물인 Graph Fourier 계수 벡터인데, Graph Fourier Transform의 반대 방향 진행은 Inverse Graph Fourier Transform라고 부르며, 다음과 같이 정의한다.

[\mathbf{f} = \mathbf{U}^T \hat{\mathbf{f}} = \Sigma_i \hat{f_i} \mathbf{u_i}]

Spectral Graph Filtering

본 Chapter의 내용은 이후에 GFT를 어떻게 적용하느냐에 관한 내용인데, 간단하게만 짚고 넘어가겠다. 추후 다른 글에서 자세히 다루도록 할 것이다.

GFT를 통해 우리가 얻고자 하는 것은, Graph 내에 있는 어떠한 중요한 특성을 포착하는 것이다. 그리고 이 목적은 Graph Filtering이라는 과정을 통해 구체화할 수 있다.

Graph Filtering은 크게 Spectral Filtering과 Spatial Filtering으로 구분할 수 있으며, spectral이란 단어는 Graph 인접 행렬의 eigenvalue와 eigenvector를 구한다는 뜻을 내포한다.

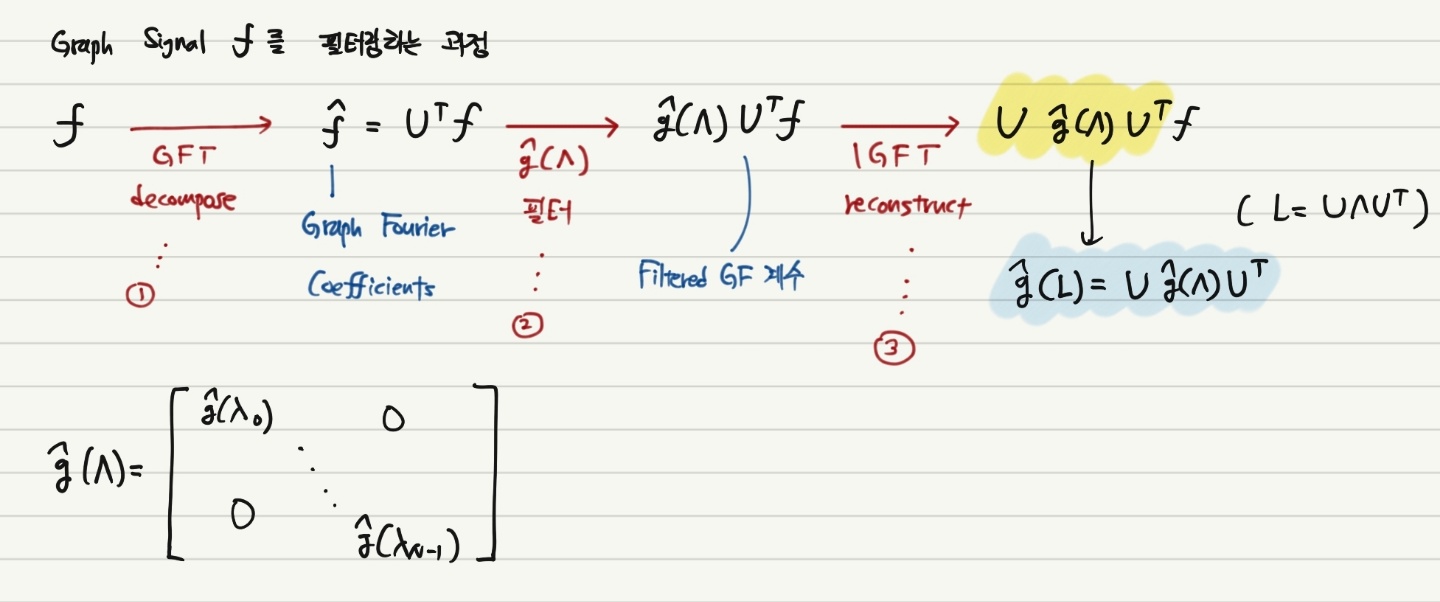
1번 과정에서 GFT를 적용하여 Signal을 변환하여 Graph Fourier 계수를 얻었다. 이후 2번 과정에서 $\hat{g(\Lambda)}$ 으로 정의되는 필터를 곱한 후 IGFT 과정을 통해 최종 결과물을 얻는다.

위 과정은 앞서 기술하였듯이 Input Signal $\mathbf{f}$ 혹은 Input Data $\mathbf{X}$ 가 주어졌을 때, 특정한 필터를 선택하여 곱합으로써 이 Input에서 중요한 특성을 추출하는 의미를 갖는다.

이를 다시 표현하면,

[g_{\theta} * x = \mathbf{U} g_{\theta} \mathbf{U}^T x]

여기서 $\theta$ 는 파라미터를 의미하는데, 이 파라미터의 학습 가능 여부에 따라 다른 방식으로 문제를 풀어나갈 수 있다.

이후 위 식을 통해서 Graph Convolution을 정의하는 과정으로 내용이 이어지게 된다.

References

1. GCN 논문
2. CS224W Spectral Clustering 강의
3. 푸리에 변환 설명 블로그 글

본 글은 Windows10 환경에서 Minikube를 설치하는 과정을 기록한 글이다.

이미지가 잘 보이지 않는다면, 새 탭에서 이미지 열기를 누르시길 바랍니다.

1. Minikube 설치 및 동작 확인

Minikube 설치는 본 문서를 참고하였다. 명령 프롬프트를 관리자 권한으로 실행한 후 아래와 같은 메시지를 출력해보자.

systeminfo

아래와 같은 문구를 발견하였다면 Hypervisor를 사용할 준비가 된 것이다.

만약 펌웨어에 가상화 사용이 아니오로 되어 있다면 BIOS 모드로 들어가서 이를 변경해주어야 한다.

설치 문서에 따르면 Hypervisor로 Hyper-V 또는 VirtualBox를 선택할 수 있다고 한다. 필자의 경우 Windows Home을 사용하고 있었기 때문에 VirtualBox를 설치하였다. 설치 링크는 이 곳이며 아래 색칠된 링크를 클릭하여 다운로드를 진행하면 된다.

이제 Chocolatey를 이용하여 Minikube를 설치해보자.

물론 Chocolatey를 사용하지 않아도 설치할 수 있지만, 과정이 상당히 간단하므로 이를 추천한다. Chocolatey 설치 링크는 이 곳이며 아래와 같은 Command를 입력하면 된다.

Chocolatey 설치가 완료되었으면 아래 Command를 통해 Minikube를 설치한다.

이제 Minikube를 구동시킬 차례이다. 시작/작업/중지/삭제 과정을 거치게 되는데 작업을 제외한 커맨드는 아래와 같다.

minikube start
minikube stop
minikube delete

위 그림은 Minikube를 start한 후 stop 했을 때 까지의 과정을 보여주며, start 이후 status command를 입력했을 때 2번째 그림과 같은 화면을 확인할 수 있다.

본격적인 작업은 다음 Chapter에서 설명하도록 하고, 일단 중지한 Minikube 클러스터를 삭제해보자.

당황스러운 메시지를 확인할 수 있는데, 이는 지금 Hypervisor가 실행되고 있기 때문이다. 작업 관리자를 켜서 모두 종료해준다.

다시 시도해보면 아래와 같이 삭제가 완료되었음을 알 수 있다.

2. Kubernetes, Kustomize, k9s

Minikube를 이용하면 복잡한 Kubernetes 설치 과정을 생략할 수 있다.

Kustomize는 Kubernetes 오브젝트의 배포를 보조하는 도구인데, Kubernetes 1.14 버전 이상을 사용하면 따로 설치가 필요하지 않다. 즉, 지금까지의 과정을 마쳤으면 Kubernetes, Kustomize 까지 준비가 된 것이다.

일반적으로 Kubernetes를 사용하기 위해서는 kubectl이라는 커맨드 라인 툴을 사용하는데, 로그 및 모니터링 등 작업에 대한 편의성이 떨어지기 때문에 k9s라는 툴이 사용된다고 한다. k9s는 이 곳에서 다운로드 받을 수 있다.

앞서 Windows 환경에 적합한 chocolatey를 설치했기 때문에 이를 이용하여 설치를 진행해보자. 이렇게 간단할 수가 없다.

choco install k9s

성공적으로 설치가 완료되었다. 다음을 입력해보면,

k9s

위와 같은 초기 화면을 확인할 수 있다. 우측 상단에는 여러 단축키가 보이는데, 이를 활용하면 편리하게 명령을 실행할 수 있다. 콜론(:)을 누르면 명령어를 입력할 수 있게 된다. 네임스페이스의 리스트를 확인하기 위해 ns를 입력해보자.

kube-system을 방향키로 선택한 후 엔터를 입력하면 이 곳에 속한 파드 리스트를 확인할 수 있다.

References

1. 쿠버네티스에서 머신러닝이 처음이라면! 쿠브플로우!, 이명환 저
2. Minikube 설치 문서
3. k9s 깃헙

본 글은 Local 환경에서 Standard 모드로 설치한 Kubeflow에 대한 튜토리얼 내용을 담고 있다. WSL2-Ubuntu 환경에서의 Kubeflow 설치 방법에 대해 확인하고 싶다면 이전 글을 참고하길 바란다.

1. Notebook Servers

1.1. 노트북 생성

노트북 서버는 Kubernetes 위에서 실행되는 Jupyter Notebook 서버를 의미한다.

+NEW SERVER를 눌러 필요한 설정에 맞게 항목을 입력해준 뒤, Launch 버튼을 클릭하면 노트북 생성이 시작된다.

생성 완료 후 화면은 아래와 같다.

필자는 Dashboar에 처음 접속할 당시 Namespace를 Youyoung으로 지정하였다. 따라서 방금 생성한 노트북은 이 Namespace 아래에 생성된다. 확인해보자.

kubectl get pods –all-namespaces
kubectl get pods -n Youyoung

방금 생성한 testgraph가 보인다.

1.2. 노트북 사용

위 화면에서 CONNECT를 클릭하면 익숙한 Jupyter 환경이 보인다.

2. Pipeline Quickstart

2.1. Data Passing in python components 튜토리얼 실행

Kubeflow 파이프라인은 컨테이너 기반의 ML 워크플로우를 생성/배포할 수 있게 해주는 툴이다. 확장성과 재사용성이 좋아 편리하게 사용할 수 있다. 첫 튜토리얼을 위해서는 공식 문서 가이드에 친절한 설명을 따라가면 된다. 튜토리얼 파이프라인을 클릭해보자.

이후 +Create Experiment 버튼을 클릭하고 Experiment Name에 My experiment를 입력해주자. 다음 화면에서 Run Name을 My First Run으로 해준 후, Start 버튼을 누르자.

잠시 기다린 후 Run name을 클릭하면 아래와 같이 실행된 Graph의 Component들을 확인할 수 있다.

Config 탭을 누르면 세부 사항을 확인할 수 있다.

2.2. Source 코드 확인

소스코드 페이지를 확인해보고 넘어가자. 먼저 서두의 주석을 확인하자.

1) Kubeflow 파이프라인은 Component 인스턴스를 생성하고 이들을 연결함으로써 구성됨  
2) 각 Component는 Input/Output을 가짐. Component 간 연결은 이 Input/Output 연결을 통해 이뤄짐  
3) 한 Task의 Output을 다른 Task의 Input에서 argument로 취급함  

데이터는 Small Data와 Bigger Data가 존재한다. Small Data는 커맨드 라인의 인자로 전달되며 수 킬로바이트를 초과하면 안된다. 예를 들면 숫자, URL, 칼럼 명 등이 이에 해당할 것이다. 작은 리스트나 딕셔너리 혹은 JSON 구조도 괜찮지만 용량 체크는 필수적이다.

Small Data는 string으로 serialized 되었다가 커맨드 라인 인자로 전달될 때 deserialized 되는데, str, int, float, bool, list, dict의 경우 빌트인 serializer를 통해 이 과정이 자동으로 수행되지만 그 외의 경우 직접 data를 반환하기 전에 serialized 되어 있어야 한다.

Bigger Data는 파일로부터 읽기/쓰기된다. 이 때 Input/Output 파일은 문자열로서 함수로 전달된다. InputPath 파라미터를 쓰면 함수는 이에 상응하는 input data를 파일로서 consume한다. 데이터는 다운로드 된 후 로컬 파일로 쓰여진 후, 그 위치(path)를 함수에게 전달할 것이다. OutputPath 파라미터는 반대로 output data를 파일로 생성하고 이를 storage 시스템에 업로드하여 이후의 components에게 전달될 수 있도록 하는 역할을 수행한다. 전달되는 데이터의 Type 역시 명시적으로 지정할 수 있다. OutputPath('TFModel')과 같이 말이다.

자 이제 Bigger Data를 쓰기/읽기 해볼 것인데, 먼저 이전에 확인했던 예제 Graph의 구조를 다시 한 번 확인해보자.

Repeat line, Print Text 부분을 먼저 살펴보자.

from typing import NamedTuple
import kfp
from kfp.components import func_to_container_op, InputPath, OutputPath

# Writing bigger data
@func_to_container_op
def repeat_line(line: str, output_text_path: OutputPath(str), count: int = 10):
    '''Repeat the line specified number of times'''
    with open(output_text_path, 'w') as writer:
        for i in range(count):
            writer.write(line + '\n')

# Reading bigger data
@func_to_container_op
def print_text(text_path: InputPath()):
    # The "text" input is untyped so that any data can be printed
    '''Print text'''
    with open(text_path, 'r') as reader:
        for line in reader:
            print(line, end = '')
            
# 먼저 repeat_line, print_text 함수를 정의한다.
# 이 때 각각의 함수는 인자로 OutputPath와 InputPath를 사용하는 것에 주목하자.
# repeat_line의 경우 OutputPath에 쓸 대상을 전달하고,
# print_text의 경우 InputPath에 읽을 대상을 전달한다.

# 이제 실제로 실행시킬 함수를 정의하자
def print_repeating_lines_pipeline():
    repeat_lines_task = repeat_line(line='Hello', count=5000)
    print_text(repeat_lines_task.output) # Don't forget .output !

# Submit the pipeline for execution:
kfp.Client(host=kfp_endpoint).create_run_from_pipeline_func(
    print_repeating_lines_pipeline, arguments={})

다음 단계로 넘어간다.

# ### Processing bigger data
@func_to_container_op
def split_text_lines(
    source_path: InputPath(str),
    odd_lines_path: OutputPath(str),
    even_lines_path: OutputPath(str)
    ):
    with open(source_path, 'r') as reader:
        with open(odd_lines_path, 'w') as odd_writer:
            with open(even_lines_path, 'w') as even_writer:
                while True:
                    line = reader.readline()
                    if line == "":
                        break
                    odd_writer.write(line)
                    line = reader.readline()
                    if line == "":
                        break
                    even_writer.write(line)

def text_splitting_pipeline():
    text = '\n'.join(['one', 'two', 'three', 'four', 'five',
        'six', 'seven', 'eight', 'nine', 'ten'])
    split_text_task = split_text_lines(text)
    print_text(split_text_task.outputs['odd_lines'])
    print_text(split_text_task.outputs['even_lines'])

# Submit the pipeline for execution:
kfp.Client(host=kfp_endpoint).create_run_from_pipeline_func(
    text_splitting_pipeline, arguments={})

이제 마지막 단계이다.

# Writing many numbers
@func_to_container_op
def write_numbers(numbers_path: OutputPath(str), start: int = 0, count: int = 10):
    with open(numbers_path, 'w') as writer:
        for i in range(start, count):
            writer.write(str(i) + '\n')


# Reading and summing many numbers
@func_to_container_op
def sum_numbers(numbers_path: InputPath(str)) -> int:
    sum = 0
    with open(numbers_path, 'r') as reader:
        for line in reader:
            sum = sum + int(line)
    return sum


# Pipeline to sum 100000 numbers
def sum_pipeline(count: int = 100000):
    numbers_task = write_numbers(count=count)
    print_text(numbers_task.output)

    sum_task = sum_numbers(numbers_task.outputs['numbers'])
    print_text(sum_task.output)


# Submit the pipeline for execution:
kfp.Client(host=kfp_endpoint).create_run_from_pipeline_func(
    sum_pipeline, arguments={})

# Combining all pipelines together in a single pipeline
def file_passing_pipelines():
    print_repeating_lines_pipeline()
    text_splitting_pipeline()
    sum_pipeline()

if __name__ == '__main__':
    # Compiling the pipeline
    kfp.compiler.Compiler().compile(file_passing_pipelines, __file__ + '.yaml')

2.3. pods status 확인

만약 어떤 pipeline을 실행하고 있는 과정에서 아래와 같이 Status가 Pending execution이라면 Container를 생성하고 있는 중일 것이다.

아래 명령어를 통해 본인이 생성한 Kubeflow의 Namespace에 있는 pods의 상태를 확인할 수 있다.

kubectl get pods -n {YOUR_NAMESPACE}

시간이 지나면 위와 같이 running 상태로 바뀔 것이다.

References

Kubeflow Pipelines QuickStart

본 글에서는 GDC: Graph Diffusion Convolution의 핵심적인 내용에 대해서 정리해 볼 것이다. 논문 원본을 직접 읽어보는 것을 권하며, 논문의 저자가 작성한 노트북 파일도 참고하면 도움이 된다.

torch_geomectric을 이용하여 GDC를 사용하는 방법에 대해서 간단하게 Github에 올려두었으니 참고해도 좋을 것이다.

Diffusion Improves Graph Learning 설명

1. Background

GNN을 구성하는 데에는 다양한 요소가 존재하지만, Graph Convolution은 가장 핵심적인 부분이라고 할 수 있다. 다양한 형태의 Graph Convolution이 존재하지만 대부분의 경우 직접적인 1-hop 이웃 사이의 관계에서 message가 전달되곤 한다.

본 논문에서는 이러한 제한점을 없애고 spatially localized한 Graph Convolution을 제안하고 있다. GDC는 1-hop 이웃에서만 정보를 모으는 것이 아니라, Diffusion: 확산을 통해 더욱 큰 이웃 집합에서 정보를 통합한다.

즉 GDC는 Graph의 특징을 효과적으로 포착하고 이를 더욱 잘 구조화할 수 있게 Graph를 재정의하는 연산자로 생각하면 된다. 또한 GDC는 특정 GNN에 종속되지 않고 설계 방식에 따라 Graph 기반의 다양한 모델에 적용될 수 있다는 장점을 가진다.

2. Personalized Page Rank

갑자기 왜 주제가 바뀌었는지 의문이 들수도 있지만, PPR은 GDC의 연산 방식을 이해하기 위해서는 반드시 알아야 하는 요소이다.

이후에 설명하겠지만 GDC에는 기존 Graph 내에서 Diffusion을 통해 더욱 넓은 이웃 집합을 형성하고 정보를 통합하는 과정이 있는데, 이 때 가중치 계수로 $\theta_k$ 가 등장하고 이 가중치 계수의 메인 옵션 중 하나가 바로 PPR이다. 본 글에서의 설명은 이 PPR 계수를 중심으로 진행한다. (다른 옵션으로는 Heat Kernel이 있다.)

PageRank 논문 원본은 이 곳에서 확인할 수 있고 이에 대한 좋은 설명을 담은 블로그 글은 이 곳에서 볼 수 있다. 혹은 CS224W 4강에서 자세한 설명을 들어도 좋다.

Graph에서 Node의 중요도를 계산하는 방법에는 여러 가지가 있지만, PPR에서는 이를 다음과 같이 정의한다.

특정 Node $j$ 가 있다고 할 때 이 Node $j$ 를 향하는 Node 들의 중요도의 합이 바로 이 Node $j$ 의 중요도가 된다. 이 때 Node $i$ 에서 밖으로 뻗어 나가는 연결이 3개 존재하고, 이 중 1개가 Node $j$로 향했다고 하면, Node $i$ 가 Node $j$에 기여하는 바는 바로 $\frac{r_i}{3}$ 가 되며 이 때 $r_i$ 는 Node $i$ 의 중요도를 의미한다.

위 설명을 CS224W 강의자료로 확인하면 아래와 같다.

위 설명을 실제로 적용하기 위해서는 아래와 같은 Power Iteration Method를 적용하면 된다.

먼저 초기 중요도 벡터 $\mathbf{r}$ 을 정의한다.

[\mathbf{r}^0 = [1/N, 1/N, …]^T]

다음 식을 반복한다.

[\mathbf{r}^{(t+1)} = \mathbf{M} \mathbf{r}^t]

그리고 위 식이 아래와 같은 조건을 만족할 때 멈춘다.

[\vert \mathbf{r}^{(t+1)} - \mathbf{r}^t \vert_{1} \le \epsilon]

그런데 이 때 만약 특정 node가 Outbound Link를 가지게 않을 경우 더 이상 업데이트되지 못하고 갇히는 현상이 발생하는데, 이를 위해 일정 확률로 Random 하게 다른 node로 teleport하도록 설정하면 이 문제를 해결할 수 있다.

최종적으로 PageRank 식은 아래와 같이 정의할 수 있다. 아래 식은 node j로 향한 Importance Estimate의 합이 곧 이 node j의 새로운 Importance Estimate임을 의미한다.

[r_j = \Sigma_{i \rightarrow j} \beta \frac{r_i}{d_i} + (1-\beta) \frac{1}{N}]

위 식의 경우 $\beta$ 의 확률로 link를 따라가고, $1-\beta$ 의 확률로 teleport해야 함을 뜻한다.

위 식을 벡터/행렬화 하면 아래와 같다.

[\mathbf{r} = \beta M \mathbf{r} + (1-\beta) [\frac{1}{N}]_{N * N}]

여기에서 특정 node를 중심으로 PageRank를 구한 것이 바로 PPR이며 아래와 같이 표현한다.

[\mathbf{r} = \beta M \mathbf{r} + (1-\beta) \mathbf{a}]

[\mathbf{a} = [0, 0, …, 1, 0, …, 0]^T]

자 이제 위 식을 GDC 논문에 있는 식에서 사용한 기호로 바꾸기 위해 $1-\beta$ 를 $\alpha$ 로, $M$ 을 $T$로 변환한다.

[\mathbf{r} = \alpha \mathbf{a} + (1-\alpha) \mathbf{r} \mathbf{T}]

위 점화식은 아래와 같이 다시 표현할 수 있다.

[\mathbf{r} = \Sigma_{k=0}^{\infty} \alpha (1-\alpha)^k \mathbf{T}^k]

[k=0, \mathbf{r} = \alpha \mathbf{a}]

[k=1, \mathbf{r} = \alpha \mathbf{a} + (1-\alpha) \mathbf{r} \mathbf{T}]

[k=2, \mathbf{r} = \alpha \mathbf{a} + (1-\alpha) \alpha \mathbf{a} \mathbf{T} + (1-\alpha)^2 \alpha \mathbf{a} \mathbf{T}^2]

그리고 이제 우리는 드디어 PPR 가중치 계수를 얻을 수 있다.

[\theta_k^{PPR} = \alpha (1-\alpha)^k]

참고로 계산을 위해 위 식을 기하 급수를 이용하여 재표현하면 아래와 같다.

[r_j = \frac{\alpha} {1- (1-\alpha) r_j}]

3. GDC 수행 과정

지난 Chapter에서 PPR 계수를 구하는 방법에 대해 알았으니 이제는 GDC를 연산하는 과정에 대해 설명할 것이다.

GDC는 아래와 같이 크게 4가지의 과정을 거쳐 수행된다.

1) Transition Matrix $\mathbf{T}$ 를 계산한다. (symmetric 버전)

[\mathbf{T} = \mathbf{D}^{-\frac{1}{2}} \mathbf{A} \mathbf{D}^{-\frac{1}{2}}]

2) 아래 식을 통해 $\mathbf{S}$를 얻는다.

[\mathbf{S} = \Sigma_{k=0}^{\infty} \theta_{k} \mathbf{T}^k]

3) 특정 임계 값을 넘지 못하는 작은 값들은 0으로 만듦으로써 위 결과물을 sparsify한다.
(Top-K 방식을 채택할 수도 있다.)

[\tilde{\mathbf{S}} = spar(\mathbf{S})]

4) 최종적으로 Transition Matrix $\mathbf{T}_{\tilde{\mathbf{S}}}$ 를 계산한다.

[\mathbf{T}{\tilde{\mathbf{S}}} = \mathbf{D}^{-\frac{1}{2}}{\tilde{\mathbf{S}}} \tilde{\mathbf{S}} \mathbf{D}^{-\frac{1}{2}}_{\tilde{\mathbf{S}}}]

정리하자면, 2까지의 과정을 통해 Diffusion을 수행해서 좀 더 넓은 범위를 커버하게 만드는 것이고, 여기서 마치면 새로 계산된 $\mathbf{S}$ 는 Dense Matrix이기 때문에 희소화과정을 통해 중요도가 낮다고 판단되는 값들을 모두 0으로 masking해주는 작업을 3에서 수행한다는 뜻이다.

위 과정 외에도 수식의 완결성을 위한 장치가 여럿 있는데 이는 논문 원본을 참조하길 바란다.

지금까지의 과정을 그림으로 나타내면 아래와 같다.

4. 결론

GDC는 spetral한 방법론의 장점을 취하면서도 단점은 취하지 않는다는 특징을 지닌다. GDC가 기초로하는 가정은 homophily(동질성, 연결된 node는 비슷한 성질을 지님)가 만족한다 인데, 이 가정이 통하지 않는 데이터셋에는 경우에 따라 효과적이지 못할 수 있다.

적은 수의 Hyper-parameter를 갖고 있고 응용 범위가 넓기 때문에 다양한 데이터셋과 환경에서 실험 요소로 적극 활용할 수 있을 것으로 보인다.

글 서두의 링크에서도 언급하였듯이 torch_geometric을 통해 적용 방법을 찾는 것이 효율적일 것이다.

References

1) 논문 원본
2) 논문 저자의 깃헙 주소 3) Stanford University CS224W Lecture

본 글에서는 2021년 연말 SPAC 상장이 예상되는 nextdoor에 대해 소개하고, 비즈니스 모델에 대해 분석한 뒤 향후 전망에 대한 의견을 담아 볼 것이다. 2021년 8월에 작성되었으며, 시간이 지남에 따라 기술된 내용에는 변화가 발생할 수 밖에 없으므로 참고용으로만 활용하길 바란다.

1. nextdoor 소개

한국인에게 중고 거래, 지역 커뮤니티하면 당근마켓이 제일 먼저 떠오를 것이다. 그 외에 번개장터나 중고나라 또한 예시로 들 수 있지만, 아마 정말로 Hyperlocal 혹은 동네 생활권 커뮤니티를 지향하는 회사는 당근마켓이 아닐까 생각해 본다.

2008년에 설립되어 2011년부터 본격적으로 서비스를 시작한 지역 밀착형 SNS, 혹은 Hyperlocal 커뮤니티를 형성하는 플랫폼 기업으로 기반을 다지고 있는 nextdoor는 2020년 Covid19 발생 이후 사람 간의 만남을 기반으로 하는 비즈니스 모델을 갖고 있음에도 불구하고 괄목할만한 성장을 이루어 냈다.

이러한 성장 스토리에는 굉장히 많은 요인이 개입되어 있겠지만, 간단히 nextdoor의 이용자들의 행동 양태를 생각해보면 이렇다. Covid19으로 인해 먼거리를 이동하거나 자유롭게 다양한 지역을 돌아다니는 움직임은 크게 줄었다. 그런데 사실 아무리 온라인 쇼핑이 편하고, 배달에 익숙해졌다 하더라도 어쩔 수 없이 다른 사람과의 만남을 이어가야만 살아갈 수 있는 존재이다. 이러한 맥락에서 비록 Covid19로 인해 행동 반경은 좁아졌지만 그 좁아진 생활권 속에서 nextdoor의 사업 모델이 빛을 발했다고 볼 수 있다.

nextdoor의 사용자는 약 6000만명 수준이라고 한다. (미국을 포함하여 12개 국에서 서비스되고 있다.) 더 놀라운 것은 2700만명 정도가 매주 접속을 한다는 것인데, 그만큼 진성 사용자의 수가 많다는 것이고, 이는 곧 이 사용자들을 대상으로 하는 비즈니스는 더욱 효율이 좋을 가능성이 높다는 뜻을 의미한다.

다음 Chapter에서는 nextdoor의 비즈니스 모델에 대해 알아본다.

2. Business Model

2.1. nextdoor가 제공하는 서비스

nextdoor에는 27만여 개에 달하는 커뮤니티가 있다고 한다. nextdoor는 지역 사회를 구성하고 있는 여러 구성원들 사이의 연결을 돕고, 그들이 어떤 커뮤니티를 형성하는 것을 지원하며 이러한 네트워크 속에서 사업 기회를 찾는 기업들로부터 광고비를 비롯한 수수료를 수취하는 사업 모델을 갖고 있다.

nextdoor 홈페이지를 보면, nextdoor가 어떻게 돈을 벌고 있는지에 대한 간략한 설명이 나온다.

3번의 경우 중고 거래로 이해할 수 있을 것이다. 아무래도 1번에 해당하는 광고 수입이 매출의 주 원천이 될 것인데, nextdoor의 커뮤니티가 더욱 단단해지고 사용자가 증가함에 따라 수수료의 규모도 굉장히 커질 것으로 기대된다.

그렇다면 nextdoor의 이용자는 어떻게 가입을 하고 어떤 혜택을 누릴 수 있을까? nextdoor는 지역 기반 서비스이기 때문에, 사용자가 속한 지역에 대한 정보가 매우 중요하다. 집을 임대/소유하고 있거나 집을 지을 계획을 갖고 있거나 rental property를 갖고 있을 경우 특정 이웃 집단에 소속될 수 있다. 이에 대한 검증 역시 이루어지며, 사용자는 실명을 통해 가입해야 한다.

가입 후 아래와 같은 혜택을 누릴 수 있다.

• 여러 지역 활동에 대한 커뮤니티의 추천을 받을 수 있다. (예: 식당, 공원 등)
• 지역 뉴스에 대한 업데이트를 받을 수 있다.
• 범죄 경보를 받을 수 있다.
• 여러 중고 물품을 구매/판매할 수 있다.
• 서비스를 사고 팔 수 있다. (예: 베이비시터, 반려견 산책 등)

혹자는 위 서비스가 무엇이 그리 대단하냐고 생각할 수도 있다. 맛집은 구글이나 네이버 같은 곳에서 검색하면 되고, 뉴스는 TV나 Youtube, 포털 사이트 등을 보면 되는 것 아니냐고. 물론 그럴수도 있다. 그런데 nextdoor가 만든 서비스는 색깔이 좀 다르다.

일단 일반적인 검색을 통해 찾는 정보보다 훨씬 자세하며, 업데이트 속도도 빠르다. 그럴 수 밖에 없다. 길 건너편에 있는 한 작은 주택 근처에서 발생한 일은 기자도, 정치인도, 구글 직원도 아닌 그 근처에 살고 있는 사람이 제일 먼저 알아낼 확률이 더 높다. 그리고 주변에 사는 사람들이 아니라면 이러한 작은 일에 큰 관심을 갖기 어렵다. 실제로 nextdoor를 이용하는 사용자들이 자연 재해나, 질병 등과 관련한 정보를 주고 받아 지역 사회가 힘을 합쳐 위기를 극복해 난 사례는 여러 언론을 통해 보도된 바 있다.

넥스트도어의 지역 중점 기능이 빛을 발한 것은
지난 2월 텍사스주에 한파가 닥치면서 대략 430만 가구가 정전사태에 빠졌던 때였다.

넥스트도어를 기반으로 한 네트워크로 동네 주민들은 물이나 난방기구 등 생필품을 나눌 방안을 모색했다.
넥스트도어의 발표에 의하면, 한파 기간 동안 텍사스 지역의 게시물 수는 전 주보다 471% 증가했으며,
도움을 요청하거나 도움을 준 대화는 무려 400%가량 증가했다.
전력, 물, 장작, 수도관, 난방과 같이 재난 상황에서 필요한 키워드 검색량도 140% 늘어났다.

이러한 선행 사례를 통해서 지역 주민끼리 서로 돕고자 하는 마음을 확인한 넥스트 도어는
지난 5월 ‘헬프맵’이라는 서비스를 시작했다.
헬프맵은 이웃에게 도움을 줄 수 있는 내용을 기재해두면
해당 도움이 필요한 이웃이 연락을 취하는 방식으로 진행되고 있다.

출처 : 한국연예스포츠신문(http://www.koreaes.com)

물론 사용자가 증가함에 따라 정치 성향을 담은 게시글, 인종 차별 등 혐오를 담은 게시물 등이 늘어나고 이에 따른 부작용 또한 증가하고 있다. 실제로 사용자들 중 이에 대한 불쾌감을 표시하는 이들이 증가하고 있다고 한다.

필자는 사실 이러한 부분은 Social Network에 기반한 사업이라면 필연적으로 겪을 수 밖에 없다고 생각한다. Facebook이나 Twitter 등에 가짜 뉴스가 난무하고 개인 정보 유출이 발생하며, 타인을 배려하지 않는 공격적인 게시물로 인해 사회적 혼란이 발생하는 등의 문제는 이미 전 세계인들에게 있어 일상이 되었다. 물론 일상이 되었다고 해서 이에 대해 무감각해지고 대처를 소홀히 한다면 nextdoor의 미래가 밝다고 이야기할 수 없을 것이다. 다만 이와 같은 논란이 발생하는 것 자체가 문제라기 보다는 nextdoor가 이러한 문제를 어떻게 현명하게 해결해 나갈지 지속적으로 추적하는 것이 중요하다고 판단된다.

SNS의 대명사 Facebook이 Neighborhood라는 서비스를 시범적으로 출시한 것은 nextdoor에게 악재라고 볼 수 있다. CEO Sarah Friar는 언론 인터뷰에서 빅테크 기업의 지역 커뮤니티 사업으로의 진출은 크게 개의치 않는다고 했는데, 왜냐하면 신뢰할 수 있는 플랫폼을 만드는 것은 굉장히 오랫동안 공들여야 하는 작업이기 때문이다.

Facebook이 Neighborhood라는 서비스를 메인 앱과 다소 분리시킨 의도도 생각해 보아야 한다. 최근에는 논란이 가라앉긴 했지만 개인정보 유출과 관련하여 크게 곤혹을 치른 기업이 Facebook이다. 만약 내가 거주하는 지역 근처의 사람들에게 내가 알리고 싶지 않은 수많은 정보를 노출하게 된다면? Facebook이 하이퍼로컬 사업에서 성공하기 위해서는 개인정보 노출과 관련된 문제에서 자유로워야 하고, 이 때문에 별개의 앱으로 출시하진 않았지만 기존 프로필 외에 새로운 프로필을 만들게 함으로써 접근하고 있다.

정리하자면 전 세계에서 수많은 사용자를 보유하고 있는 기업이다 하더라도 지역 사회의 신뢰를 얻고, 그 구성원들이 믿고 편리하게 사용할 수 있는 기반을 만들어주는 일은 결코 쉽지 않다는 것이다.

2.2. 사용자 수, 사용 시간, ARPU 그리고 경영진

nextdoor의 사용자와 Penetration 비율은 지속적으로 증가하고 있다. 미국에서는 이미 10년 간 서비스를 개시했고, 그 과정에서 꽤 많은 진성 사용자들을 보유하게 되었다.

위 표를 보면 nextdoor의 미래에 대해 추론해 볼 수 있을 것이다. 먼저 2021년 1분기 6000만명을 기록했던 사용자 수가 얼마나 더 늘어날 것인가를 확인해야 할 것이다. 미국 인구는 정해져 있으므로 어느 순간부터는 성장률이 둔화될 수 밖에 없겠지만, 아직까지는 성장 여력이 충분하다. 미국에서 성장률이 둔화된다면 미국 외부에서의 영역 확장 속도를 높이는 것이 사용자 수 증가에 있어 관건이 될 것이다.

사용자 수가 늘어난다 하더라도 그 사용자를 통해 이익을 내지 못하면 허울 뿐인 사업 모델이 될 것이다. 이를 위해 반드시 살펴봐야 할 지표는 WAU와 ARPU이다. 많은 애플리케이션에서 제 1지표로 내세우는 MAU가 아닌 주간 지표를 핵심 지표로 세운 것은 아마 nextdoor 플랫폼의 경우 사람들의 일상 생활과 얼마나 밀접한 연관이 있는지 확인하는 것이 매우 중요하다는 점에 기인할 것이다.

WAU는 전체 사용자의 45%이고, ARPU는 2021년 1분기 기준 5$가 되었다.

위 표를 보면 nextdoor가 내년까지 ARPU를 약 30% 상승시키겠다는 목표를 수립한 것을 알 수 있다. 이는 단지 참고의 대상일 뿐이나, 최근 몇 년간 꾸준한 상승을 기록했다는 점과 규모의 경제를 달성했을 때의 이점을 생각해보면 충분히 가능한 수치로 생각해볼 수 있다.

사용자 간의 거래를 더욱 활성화시키고, 광고 수입을 늘리는 것이 주 수입원이기 때문에 경기에 일정 부분 영향을 받을 수 밖에 없다는 것 역시 고려해야 할 것이다. 하지만 무엇보다도 가장 중요한 것은 지역 사업자들 입장에서 nextdoor가 매력적인 홍보 플랫폼으로 다가와야 할 것이다.

nextdoor는 더욱 매력적인 플랫폼이 될 수 있을까?

이런 경우 경영진의 면모에 대해 검토해보면 꽤 합리적인 힌트를 얻을 수 있다. CEO Sarah Friar는 전자 결제 업체 수준에 머물던 Square에서 CFO로 근무하면서 Square를 최고의 핀테크 플랫폼 기업으로 성장시키며 IPO를 주도했던 인물이다. 이제 막 상장하면서 새로운 도약을 꿈꾸고 있는 nextdoor에게 상당히 적합한 인물이 아닐까 생각해 본다.

3. Valuation 및 투자 전략

3.1. Financial Details

고속 성장주의 재무 상황과 앞으로의 매출액, 이익 규모를 산정하는 일은 정말 어려운 일이다. 평범한 개인 투자자가 할 수 있는 일은 아마 기업의 가이던스를 보고 전망치의 온도를 달리하며 자신이 감당할 수 있는 수준을 파악하는 일이 될 것이다.

최근 nextdoor가 보여준 성과는 꽤 고무적이다. 매년 40%가 넘는 매출액 성장을 이룩하고 있으며, ARPU 역시 꾸준히 증가하고 있다. 외형 확장의 시기이기 때문에 영업/마케팅 비용이 상당할 것으로 추축되는데, 현재의 방향성을 고려해보면 규모의 경제를 달성하여 흑자 전환을 얼마나 빨리 이뤄낼 수 있느냐가 관건이 될 것으로 보인다.

플랫폼 기업 중에서도 상당히 높은 Valuation을 받고 있는 Snap이나 Pinterest, Twitter 등과 유사한 수준의 프리미엄을 받고 있다는 측면에서 nextdoor의 현재 시가 총액은 저평가라고 말하기 어렵다.

따라서 현재 시점에서의 투자는 단기간의 매출액이나 이익 규모를 보고 결정하기 보다는, 기업의 장기 시계열적 관점에서 바라보아야 할 것으로 보인다.

3.2. Investment Strategy

2021년 8월 기준으로 nextdoor의 주가는 10$ 수준이다. 이는 사실 공모가와 다를 것이 없으며 SPAC 투자자나 PIPE 투자자들의 평균 매수 단가도 이와 같은 수준일 것이다.

4분기가 되어서야 합병에 대한 구체적인 소식이 들려올 것으로 보이기 때문에 2021년 하반기를 여유있게 지켜보면서 접근하는 것이 현명할 것으로 판단한다.