목차

• Neural Discrete Representation Learning
  • 초록(Abstract)
  • 1. 서론(Introduction)
  • 2. 관련 연구(Related Work)
  • 3. VQ-VAE
    • 3.1 Discrete Latent variables
    • 3.2 Learning
    • 3.3 Prior
  • 4. 실험(Experiments)
    • 4.1 Comparison with continuous variables
    • 4.2 Images
    • 4.3 Audio
    • 4.4 Video
  • 5. 결론(Conclusion)
  • 참고문헌(References)

이 글에서는 2017년 NIPS에 게재된 Neural Discrete Representation Learning(흔히 VQ-VAE라 부른다) 논문을 살펴보고자 한다.

중요한 부분만 적을 예정이므로 전체가 궁금하면 원 논문을 찾아 읽어보면 된다.

Neural Discrete Representation Learning

논문 링크: Neural Discrete Representation Learning

Github(not official?): https://github.com/1Konny/VQ-VAE

• 2017년 11월, NIPS 2017
• DeepMind
• Aaron van den Oord, Oriol Vinyals, Koray Kavukcuoglu

초록(Abstract)

어떠한 지도 없이 유용한 표현을 학습하는 것은 머신 러닝의 핵심 과제로 남아 있다. 본 논문에서는 이러한 이산 표현을 학습하는 간단하면서도 강력한 생성 모델을 제안한다. 제안하는 VQ-VAE(Vector Quantised-Variational AutoEncoder) 모델은 두 가지 면에서 VAE와 다르다:

1. Encoder network는 연속적인 codes를 생성하나 VQ-VAE는 이산 codes를 출력한다.
2. Prior는 정적(static)이지 않고 대신 학습이 가능하다.

이산 잠재 표현을 학습하기 위해 벡터 양자화(VQ: Vector Quantisation)의 아이디어를 통합하였다. VQ 방법을 사용하면 모델이 강력한 autoregressive decoder와 짝을 이룰 때 latent들이 무시되는 “Posterior Collapse” 문제(VAE framework에서 곧잘 나타난다)를 피할 수 있다.

이러한 표현을 autoregressive prior와 짝지으면 모델은 고품질 image, video, audio을 생성할 수 있을 뿐만 아니라 speaker conversion 및 음소의 비지도 학습을 수행하여 학습된 표현이 유용함을 보일 수 있다.

1. 서론(Introduction)

Image, audio, video를 생성하는 분야에서는 많은 발전이 있었다. 어려운 과제인 few-shot learning, domain adaptation, RL 등은 학습된 표현에 크게 의존하였으나 일반적 표현을 얻는 것은 여전히 한계가 있다. Pixel domain에서 가장 효과적인 모델은 PixelCNN(1, 2)이지만, 연속적인 표현을 사용한다. 이 논문에서는, 연속(continuous)이 아닌, 이산적(discrete)인 표현을 다룬다.

언어는 본질적으로 이산적인 성질을 가지며(단어의 수는 한정적이며, 단어와 단어 사이 중간쯤이 명확히 정의되지 않음을 생각하면 된다), 음성도 비슷한 특성을 가진다. 이미지는 언어로 표현될 수 있다. 이러한 점에서, 이산적인 표현은 이러한 이산적인 domain에 잘 맞을 것이라 생각할 수 있다.

이 논문에서는 VAE와 이산표현을 결합한 새로운 생성모델(VQ-VAE)을 제안한다. Vector Quantisation(VQ)를 사용하여 너무 큰 분산으로 생기는 어려움을 피하면서 학습하기 편하고 Posterior Collapse 문제를 회피할 수 있다. 그러면서도 연속표현을 사용하는 모델과 비등하면서도 이산표현의 유연함을 제공한다.

VQ-VAE는 데이터 공간을 효과적으로 사용할 수 있게 하여, 큰 차원의 데이터(이미지의 픽셀, 음성의 음소, 텍스트의 메시지 등)에서 local이라 부르는 작은 부분, noise에 집중하는 대신 중요한 feature만을 성공적으로 모델링할 수 있게 한다.

또 강력한 prior를 제공할 수 있는데, 단어나 음소에 대한 어떤 사전 지식 없이도 언어의 구조를 파악할 수 있거나, 말하는 내용은 그대로 두면서 목소리만 바꿀 수(speaker conversion)도 있다.

그래서 이 논문이 기여한 바는,

• “posterior collapse” 문제에서 자유롭고 큰 분산 문제가 없는, 이산표현을 사용하는 VQ-VAE 모델을 제안한다.
• 이산표현 모델 VQ-VAE는 연속표현 모델만큼이나 성능이 좋음을 보인다.
• 강력한 prior가 있을 때, sample은 speech/video generation과 같은 다양한 응용 분야에서 뛰어난 결과를 생성한다.
• 어떤 명시적인 지도 없이도 언어의 속성을 파악하고 speaker를 바꿀 수도 있다.

2. 관련 연구(Related Work)

VAE는 여러 방면에서 연구되어 왔지만, discrete domain을 가지는 분야에서조차 연속표현을 사용해왔다.

사실 이산적인 변수는 backprop이 불가능하여, 이산표현의 특성을 일부 가지면서도 미분이 가능하도록 대체 방안이 연구되었다. Concrete softmax 및 Gumbel-softmax가 대표적인 예이다.

또, PixelCNN, Vector Quantisation 등이 연관 분야로 수록되어 있다.

3. VQ-VAE

VAE가 가장 연관이 있을 분야라고 논문에서는 언급한다(그러나 사실 VAE가 아니라 AE에 더 가깝다고 생각되기도 한다).

VAE는 input data $x$, prior distribution $p(z)$가 주어질 때,

• 이산 latent random variable $z$에 대해 posterior distribution $q(z \vert x)$를 parameterise하는 encoder,
• input data에 대한 분포 $p(x \vert z)$를 다루는 decoder

로 구성된다.

VAE에서 내부적으로 취급하는 분포는 대개 Gaussian 분포를 따른다고 가정한다. 확장 버전은 autoregressive prior, posterior model, normalising flow, inverse autoregressive posterior 등을 포함하기도 한다.

VQ-VAE는 여기에 이산 표현을 다루도록 한다. VQ른 사용하면서, posterior과 prior distribution은 categorical하며, 이 분포로부터 생성된 sample은 embedding table을 indexing한다. 이 embeddings는 decoder의 입력으로 들어간다.

3.1 Discrete Latent variables

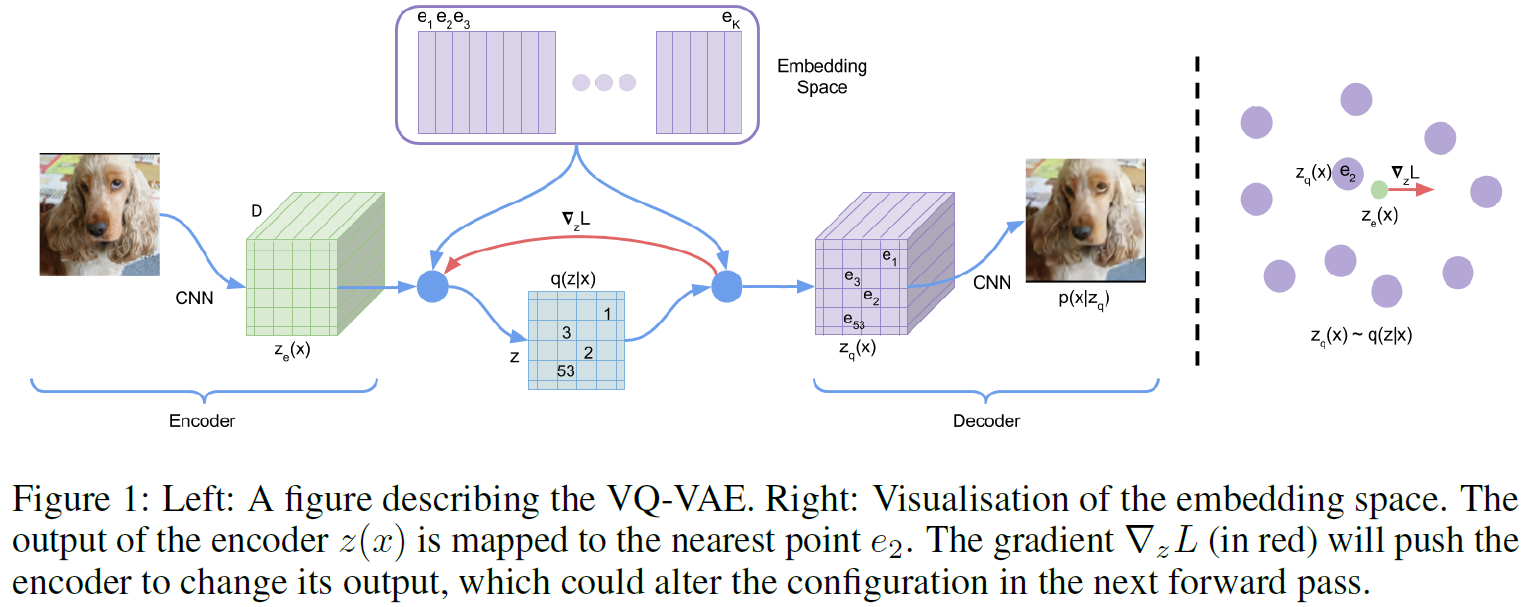
위 그림에서 embedding $e \in R^{K \times D}$가 이산표현을 나타낸다. 이를 codebook이라 하며, $K$는 이산 표현 공간의 크기($K$-way categorical과 같음), $D$는 각 embedding vector $e_i$의 차원이다.

즉 $e_i \in R^D, i \in 1, 2, …, K$이며, embedding vector가 $K$개가 있는 것이다.

모델의 encoder는 입력 $x$를 받아 $z_e(x)$를 출력한다. 이산표현벡터 $z$는 embedding space $e$에서 가장 가까운 embedding vector를 찾는다(look-up).

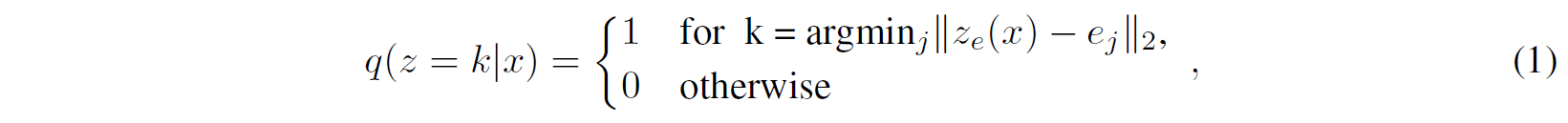
그래서 이 모델을 VAE라 할 수 있으며(논문 주장), $\log p(x)$를 ELBO로 bound할 수 있다. 제안한 분포 $q(z=k \vert x)$는 deterministic하고 $z$에 대해 단순균등 prior를 정의함으로써 KL divergence를 상수($\log K$)로 얻을 수 있다.

표현 $z_e(x)$는 식 1, 2에 주어진 대로 임베딩 $e$ 중 가장 가까운 원소를 찾고 discretisation bottlenect으로 전달된다.

3.2 Learning

한 가지 중요한 점은 식 2에서는 real gradient가 없다는 점이다.

• 이는 straight-through estimator와 비슷한 방법을 사용하여 gradient를 근사할 수 있다.
• decoder input $z_q(x)$를 encoder output으로 gradient를 복사하면 된다.
• Quantisation operation을 통해 subgradient를 사용할 수도 있지만, 본 논문의 실험에서는 위의 단순한 estimator만으로도 충분했다.

Forward에서는 $z_q(x)$가 decoder로 전달된다.
Backward에서는 gradient $\nabla_zL$이 encoder로 그대로 전달된다.

Encoder의 출력과 Decoder의 입력은 $D$ 차원의 같은 공간에 존재하여, gradient가 어떻게 변화해야 하는지 정보를 줄 수 있다.

전체 objective는 다음 식으로 표현된다.

1. 1번째 항은 reconstruction loss으로 위에서 설명한 estimator를 통해 decoder와 encoder를 모두 최적화한다.
2. 임베딩 $e_i$는 어떤 gradient도 받지 못하기 때문에 Vector Quantisation(VQ)를 사용한다.
   • VQ objective는 각 e를 encoder의 출력 $z_e(x)$로 이동하게끔 한다. 이 부분이 2번째 항이다.
3. embedding space는 무한하기 때문에 $e_i$는 encoder parameter만큼 빠르게 학습되지 않을 수 있다. Encoder가 embedding과 출력이 grow할 수 있게 만들기 위해 3번째 항 commitment loss를 추가한다.

sg는 stop gradient를 의미한다. 또 $\beta$는 commitment loss의 중요도를 정하는 hyperparameter인데, 논문의 저자는 모델이 이 값에 robust하다고 한다. $\beta$는 0.1~2.0의 값에서 최종 결과가 그다지 변하지 않았으며 모든 실험에서 $\beta=0.25$를 사용했다고 한다.

Embedding $e_i$들은 벡터의 형태로 설명하였지만, ImageNet 등 image에서는 2차원 이상의 형태를 갖는다(ImageNet: 32 x 32, CIFAR10: 8 x 8 x 10). embedding vector의 수는 총 $K$개이며, k-means와 commitment loss를 계산할 때 평균을 취한다.

논문의 이 부분에는 $N$이라 되어 있는데, 이후 부분 및 다른 논문들은 embedding space(codebook)의 크기를 $K$로 쓴다.

모델 $\log p(x)$는 다음과 같다.

decoder $p(x \vert z)$는 MAP 추론으로부터 $z=z_q(x)$로 학습되었다.

따라서 $z \ne z_q(x)$인 경우에 decoder는 어떤 확률밀도도 구할 필요가 없다. 즉,

이다. Jensen’s equality를 생각하면 부등호로 바꿔 쓸 수 있다.

3.3 Prior

Discrete latents $p(z)$에 대한 prior distribution은 categorical distribution이며, feature map 안에서 다른 $z$에 의존하여 autoregressive하게 만들어질 수 있다. VQ-VAE를 학습하는 동안 prior는 상수로, 균등하게 유지된다.

학습 후에는, $z$에 대한 자동회귀 분포에 맞춰서 ancestral sampling을 통해 $x$를 생성할 수 있다.

Image에 대해서는 PixelCNN을, raw audio에 대해서는 WaveNet 모델을 사용한다. Prior와 VQ-VAE를 같이 학습시킴으로써 더 좋은 결과를 얻는 것은 추후 연구로 남겨두었다.

4. 실험(Experiments)

4.1 Comparison with continuous variables

VQ-VQE, 그냥 VAE(continuous variables 사용), VIMCO(독립 Gaussian or categorical prior)를 비교한다. 각 모델은 각각 다음과 같은 값을 갖는다.

중요한 목표는 discrete latent를 사용해도 continuous latent를 사용했을 때와 비교해서 성능이 충분히 좋은지를 확인하는 것인데, 그 목표는 달성된 듯 하다.. 이후 결과에서 생성 결과를 볼 수 있다.

4.2 Images

ImageNet의 $128 \times 128 \times 3$ 크기의 이미지를 purely deconvolutional $p(x \vert z)$를 통해 $z=32 \times 32 \times 1$의 discrete space로 압축한다($K=512$이다). 따라서 $z$의 하나의 unit에 담긴 정보는 다음과 같다.

바꿔 말하자면 42.6배 압축되었다고도 볼 수 있다. $32 \times 32$의 각 bit는 embedding space의 index를 나타내며, 9라는 숫자는 $\log K=\log(512)=9$에서 나왔다(9bit면 512개의 숫자를 표현할 수 있음을 생각하면 된다).

그리고 encoder에 의해 생성된 $z$를 갖고 prior인 PixelCNN를 학습시킨다. 이는 학습이나 sampling 속도를 크게 향상시켜주는 방법은 아니지만, 너무 디테일한 부분(noise 등)보다는 이미지의 전체적인 부분을 잡아낼 수 있도록 하는 것에 가깝다.

왼쪽 사진을 $z$로 변환했다가 VQ-VAE의 decoder로 다시 복원한 게 오른쪽 이미지들이다. 디테일은 살짝 사라졌으나(약간 blurry해짐) 거의 원상복구된 것을 볼 수 있는데, 이는 discrete encoding을 통해 차원을 매우 줄였음에도 중요한 정보는 잃지 않고 압축할 수 있음을 보여준다.

PixelCNN을 discretised $32 \times 32 \times 1$ latent space에서 학습시킨 다음 생성한 이미지는 아래에서 볼 수 있다.

DeepMind Lab 환경에서 얻은 $84 \times 84 \times 3$의 이미지에 같은 실험을 한 결과는 아래에서 볼 수 있다.

마지막으로, DM-Lab frame에서 1번째 VQ-VAE에서 얻은 $21 \times 21 \times 1$ latent space 상에서 2번째 VQ-VAE를 PixelCNN decoder로 학습시켰다. 이러한 세팅은 “posterior collapse” 문제를 피할 수 있게 해 준다. 여기서 latent variable은 단 3개만 사용하여, 전체 bit는 $3 \times 9 = 27$bit로 float32보다도 작게 된다. 결과는 그림 5에서 볼 수 있다.

4.3 Audio

참고: 생성된 오디오 샘플은 홈페이지에서 확인할 수 있다.

109명의 speaker의 음성 녹음본이 포함된 VCTK 데이터셋을 학습에 사용했다. 6 strided convolution, stride 2, window-size 4를 사용하여 원본 파일보다 64배 압축하는 데 성공했다. latent는 512차원이며, decoder는 latent와 speaker를 나타내는 one-hot embedding 모두에 의존성을 갖는다.

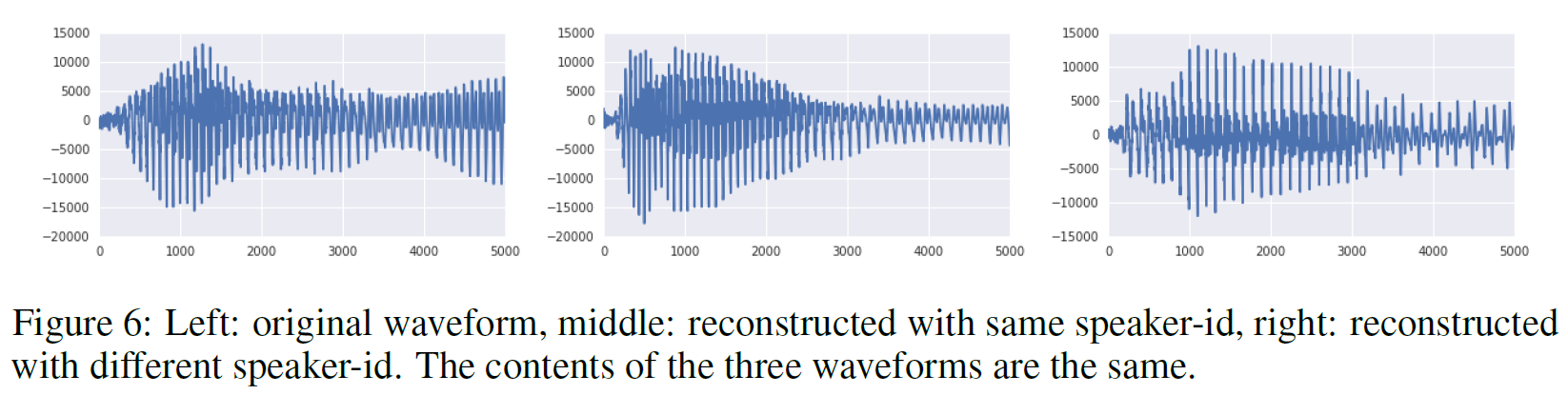
우선 VQ-VAE를 오직 long-term 상관관계(정보)만을 보존하도록 latent space를 만든 뒤 decoder로 복원하는 작업을 수행하였다. 홈페이지에서 예시를 들어보면 알 수 있겠지만, 그 내용은 변하지 않았으나 운율은 상당히 바뀐 것을 들을 수 있다. 이는 VQ-VAE가 어떤 언어적 지도 없이 고수준의 추상공간을 이해하고 중요하지 않은 부분은 버리며 음성의 내용만을 잡아냈음을 뜻한다.

다음은 unconditional sample을 분석하는 실험인데,

• audio에서 추출한 latent representation이 주어지면
• 이걸로 prior을 학습시켜 데이터의 장기(long-term) 의존성을 모델링하는 것이다.

결과적으로,

• 40960 timestep을 320 latent timestep으로 줄였다.
• 원래 WaveNet에서는 상당히 시끌벅적한?(babbling) 소리가 생성된 반면에 VQ-VAE는 상대적으로 깨끗한 소리를 생성하였다.
• 이는 가장 기본적인 음소 수준을 모델링할 수 있음을 보여준다.

3번째 실험은 speaker를 바꾸는 것이다. 즉, A라는 사람이 말한 내용을 그대로 말하되 B의 목소리로 바꾸는 것인데, 홈페이지를 가서 들어보면 꽤 잘 바뀌었다.

마지막으로 볼 것은 latent를 더 잘 이해하기 위해 각 latent를 GT phoneme-sequence와 비교한 것이다. 각 latent를 41개의 음소와 대응시켜서 classification을 수행해 보면 49.3%로 랜덤인 경우 7.2%에 비해 매우 높음을 볼 수 있다. 즉 VQ-VAE의 latent는 어떤 언어적 지도 없이도 음소 정보를 터득했다고 볼 수 있을 듯하다.

4.4 Video

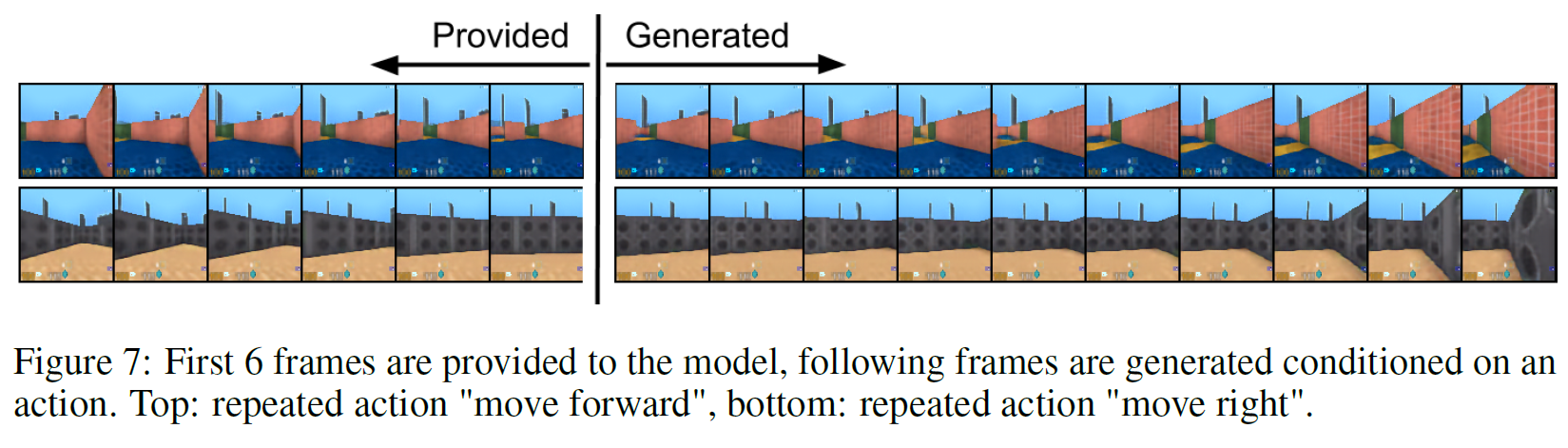
DeepMind Lab 환경에서 처음 6 frame이 주어지면 나머지 10 frame을 이어지는 내용으로 채우는 task인데, 여기서 VQ-VAE가 하는 것은 오직 latent space($z_t$) 상에서만 생성할 뿐 이미지를 직접 생성하지는 않는다.

sequence $x_i$ 안의 각 이미지는 prior model만 사용하여 모든 latent를 생성한 후 deterministic decoder로 대응되는 latent와 mapping시켜서 생성하게 된다. 따라서 VQ-VAE는 latent space 안에서만 수행하고 pixel space에서는 작업하지 않는다. 생성 결과는 아래 그림과 같다.

5. 결론(Conclusion)

• VAE와 discrete latent 표현을 위한 VQ를 결합하여 새로운 생성 모델을 만들었다.
• VQ-VAE는 long-term dependency를 잘 모델링할 수 있다.
• 원본 source를 작은 latent로 수십 배 압축할 수 있다.
• 이러한 latent는 discrete하며, continuous latent와 비교하여 성능이 필적할 만하다.
• Image, audio, video 모두에 대해서 잘 모델링 및 압축한 후 중요한 내용을 잘 보존하면서 복원이 가능하다.

즉, 이 논문은 discrete latent representation을 잘 정립한 논문이라 할 수 있겠다.

참고문헌(References)

논문 참조!