Variational AutoEncoder (VAE) 설명
31 Jul 2020 | Machine Learning Paper_Review목차
본 글은 2014년에 발표된 생성 모델인 Variational AutoEncoder에 대해 설명하고 이를 코드로 구현하는 내용을 담고 있다. VAE에 대해서 알기 위해서는 Variational Inference (변분 추론)에 대한 사전지식이 필요하다. 이에 대해 알고 싶다면 이 글을 참조하길 바란다.
본 글은 크게 3가지 파트로 구성되어 있다. Chapter1에서는 VAE 논문을 리뷰할 것이다. Chapter2에서는 먼저 논문을 간단히 요약하고, 논문의 부록에 수록되어 있었던 미분 가능한 KL-Divergence에 대한 예시를 소개할 것이다. (요약본에 대해서 먼저 보고 싶다면 2.1을 먼저 보라.) Chapter3에서는 Tensorflow를 통해 VAE를 구현할 것이다.
1. Auto-Encoding Variational Bayes 논문 리뷰
1.1. Introduction
연속형 잠재 변수와 파라미터가 다루기 힘든 사후 분포를 갖는 방향성 확률 모델에 대해 효율적인 근사 추론 및 학습을 수행할 수 있는 방법이 없을까? Variational Bayesian 접근법은 다루기 힘든 사후 분포에 대한 근사의 최적화를 내포한다.
불행히도, 일반적인 Mean-Field 접근법은 근사적 사후 분포에 대해 기댓값의 analytic한 해결법을 요구하는데 이는 보통 굉장히 intractable한 방법이다. 본 논문은 Variational Lower Bound(ELBO)의 Reparameterization이 Lower Bound의 미분 가능한 불편향 estimator를 만드는 방법에 대해 보여줄 것이다. 이 Stochastic Gradient Variational Bayes: SGVB estimator는 연속형 잠재변수나 파라미터를 갖고 있는 대부분의 모델에 대해 효율적인 근사 사후 추론을 가능하게 하며, 표준 Stochastic Gradient Ascent 스킬을 사용하여 최적화하기에 굉장히 편리하다.
iid 데이터셋이고, 데이터 포인트 별로 연속형 잠재변수를 갖고 있는 경우에 대해 본 논문은 Auto-Encoding VB 알고리즘을 제안한다. 이 알고리즘에서는 Simple Ancestral Sampling을 이용하여 근사 사후 추론을 하는 인식 모델을 최적화하기 위해 SGVB estimator를 사용하여 추론과 학습을 효율적으로 해낸다. 이 과정은 MCMC와 같이 데이터포인트 별로 반복적인 추론을 행하여 많은 연산량을 요구하지 않는 장점을 가진다.
학습된 근사 사후 추론 모델은 recognition, denoising, representation, visualization의 목적으로 활용될 수 있다. 본 알고리즘이 인식(recognition) 모델에 사용될 때, 이를 Variational Auto-Encoder라고 부를 것이다.
1.2. Method
본 섹션에서는 연속형 잠재 변수를 내포하는 다양한 방향성 그래픽 모델(Directed Graphical Model)에서 Stochastic 목적 함수인 Lower Bound Estimator를 끌어내는 과정을 설명할 것이다. 데이터포인트 별 잠재변수는 iid한 상황이라는 가정 하에 본 논문에서는 (전역) 파라미터에 대해 Maximum Likelihood와 Maximum A Posteriori 추론을 수행하고 잠재변수에 대해 Variational Inference를 수행할 것이다. 이러한 방법은 온라인 러닝에도 사용될 수 있지만 본 논문에서는 간단히 하기 위해 고정된 데이터셋을 사용할 것이다.
1.2.1. Problem Scenario
N개의 Sample을 가진 $X$ 라는 데이터가 있다고 해보자. 본 논문은 이 데이터가 관측되지 않은 연속형 확률 변수 $\mathbf{z}$ 를 내포하는 어떤 Random Process에 의해 형성되었다고 가정한다.
이 과정은 2가지 단계로 구성된다.
\[\mathbf{z}^{(i)} \sim Prior: p_{\theta^*}(\mathbf{z})\] \[\mathbf{x}^{(i)} \sim Conditional Dist: p_{\theta^*}(\mathbf{x}|\mathbf{z})\](여기서 $\mathbf{z}$는 원인, $\mathbf{x}$는 결과라고 보면 이해가 쉬울 것이다.)
이 때 우리는 위 2개의 확률이 모두 아래 두 분포의 Parametric Families of Distributions에서 왔다고 가정한다.
\[p_{\theta}(\mathbf{z}), p_{\theta}(\mathbf{x}|\mathbf{z})\]이들의 확률밀도함수는 거의 모든 $\theta, \mathbf{z}$에 대해 미분가능하다고 전제한다.
불행히도, 이러한 과정의 많은 부분은 우리가 직접 확인하기 어렵다. True 파라미터인 $\theta^*$ 와 잠재 변수의 값 $\mathbf{z}^{(i)}$ 는 우리에게 알려져 있지 않다.
본 논문은 주변 확률이나 사후 확률에 대한 단순화를 위한 일반적인 가정을 취하지 않고, 아래에서 제시한 상황처럼 분포가 intractable하고 큰 데이터셋을 마주하였을 경우를 위한 효율적인 알고리즘에 대해 이야기하고자 한다.
1) Intractability
\[\int p_{\theta}(\mathbf{z}) p_{\theta}(\mathbf{x}|\mathbf{z}) d\mathbf{z}\](1) Marginal Likelihood $p_{\theta}(\mathbf{x})$ 의 적분은 위 식으로 표현되는데, 이 식이 intractable한 경우가 존재한다. 이 경우는 Evidence가 적분이 불가능한 경우를 의미한다.
(2) True Posterior Density가 intractable한 경우 (EM알고리즘이 사용될 수 없음)
True Posterior Density는 아래와 같다.
\[p_{\theta}(\mathbf{z}|\mathbf{x}) = p_{\theta}(\mathbf{x}|\mathbf{z}) p_{\theta}(\mathbf{z})/p_{\theta}(\mathbf{x})\](3) 어떠한 합리적인 Mean-Field VB 알고리즘을 위한 적분이 불가능한 경우
이러한 Intractability는 굉장히 흔하며, 복잡한 Likelihood 함수를 갖는 신경망 네트워크에서 발견할 수 있다.
\[Likelihood: p_{\theta}(\mathbf{x}|\mathbf{z})\]2) A Large Dataset
데이터가 너무 크면 배치 최적화는 연산량이 매우 많다. 우리는 작은 미니배치나 데이터포인트에 대해 파라미터 업데이트를 진행하고 싶은데, Monte Carlo EM과 같은 Sampling Based Solution은 데이터 포인트별로 Sampling Loop를 돌기 때문에 너무 느리다.
위 시나리오에서 설명한 문제들에 대해 본 논문은 아래와 같은 해결책을 제시한다.
첫 번째로, 파라미터 $\theta$ 에 대한 효율적인 근사 ML/MAP 추정을 제안한다. 이 파라미터들은 숨겨진 Random Process를 흉내내고 실제 데이터를 닮은 인공적인 데이터를 생성할 수 있게 해준다.
두 번째로, 파라미터 $\theta$ 의 선택에 따라 관측값 $\mathbf{x}$ 가 주어졌을 때 잠재 변수 $\mathbf{z}$ 에 대한 효율적인 근사 사후 추론을 제안한다.
세 번째로, 변수 $\mathbf{x}$ 에 대한 효율적인 근사 Marginal Inference를 제안한다. 이는 $\mathbf{x}$ 에 대한 prior이 필요한 모든 추론 task를 수행할 수 있게 해준다.
위 문제를 해결하기 위해 아래와 같은 인식 모델이 필요하다.
\[q_{\phi}(\mathbf{z}|\mathbf{x})\]이 모델은 intractable한 True Posterior의 근사 버전이다.
기억해야 할 것이, Mean-Field Variational Inference에서의 근사 Posterior와는 다르게 위 인식 모델은 꼭 계승적(factorial)일 필요도 없고, 파라미터 $\phi$ 가 닫힌 형식의 기댓값으로 계산될 필요도 없다.
본 논문에서는 인식 모델 파라미터인 $\phi$ 와 생성 모델 파라미터인 $\theta$를 동시에 학습하는 방법에 대해 이야기할 것이다.
| 구분 | 기호 |
|---|---|
| 인식 모델 파라미터 | $\phi$ |
| 생성 모델 파라미터 | $\theta$ |
코딩 이론의 관점에서 보면, 관측되지 않은 변수 $\mathbf{z}$ 는 잠재 표현 또는 code라고 해석될 수 있다. 본 논문에서는 인식 모델을 Encoder라고 부를 것이다. 왜냐하면 데이터 포인트 $\mathbf{x}$ 가 주어졌을 때 이 Encoder가 데이터 포인트 $\mathbf{x}$ 가 발생할 수 code $\mathbf{z}$의 가능한 값에 대한 분포를 생산하기 때문이다.
비슷한 맥락에서 우리는 생성 모델을 확률적 Decoder라고 명명할 것인데, 왜냐하면 code $\mathbf{z}$ 가 주어졌을 때 이 Decoder가 상응하는 가능한 $\mathbf{x}$ 의 값에 대해 분포를 생성하기 때문이다.
\[Encoder: q_{\phi}(\mathbf{z}|\mathbf{x})\] \[Decoder: p_{\theta}(\mathbf{x}|\mathbf{z})\]1.2.2. The Variational Bound
Marginal Likelihood는 각 데이터 포인트의 Marginal Likelihood의 합으로 구성된다. 이를 식으로 표현하면 아래와 같다.
\[log p_{\theta}(\mathbf{x}^{(1)}, ..., \mathbf{x}^{(N)}) = \sum_{i=1}^N log p_{\theta} (\mathbf{x}^{(i)})\]그런데 데이터 포인트 하나에 대한 Marginal Likelihood는 아래와 같이 재표현이 가능하다.
\[log p_{\theta} (\mathbf{x}^{(i)}) = D_{KL} (q_{\phi}(\mathbf{z}|\mathbf{x}^{(i)}) || p_{\theta} (\mathbf{z}|\mathbf{x}^{(i)})) + \mathcal{L} (\theta, \phi; \mathbf{x}^{(i)})\]우변의 첫 번째 항은 True Posterior의 근사 KL Divergence이다. 이 KL Divergence는 음수가 아니기 때문에, 두 번째 항인 $\mathcal{L}(\theta, \phi; \mathbf{x}^{(i)})$ 는 i번째 데이터 포인트의 Marginal Likelihood의 Varitaional Lower Bound라고 한다. 변분 추론 글을 읽어보고 왔다면 알겠지만, 이는 Evidence의 하한 값을 뜻하기도 하기 때문에 ELBO라고 부르기도 한다.
부등식으로 나타내면 아래와 같다.
\[log p_{\theta} (\mathbf{x}^{(i)}) \geq \mathcal{L}(\theta, \phi; \mathbf{x}^{(i)}) = E_{q_{\phi} (\mathbf{z}|\mathbf{x})} [-logq_{\phi}(\mathbf{z}|\mathbf{x}) + log p_{\theta}(\mathbf{x}, \mathbf{z})]\]이 식은 또 아래와 같이 표현할 수 있다.
\[\mathcal{L} (\theta, \phi; \mathbf{x}^{(i)}) = -D_{KL} (q_{\phi} (\mathbf{z}|\mathbf{x}^{(i)}) || p_{\theta} (\mathbf{z}) ) + E_{q_{\phi} (\mathbf{z} | \mathbf{x}^{(i)})} [log p_{\theta} (\mathbf{x}^{(i)} | \mathbf{z}) ]\]우리는 Lower Bound $L(\theta, \phi; \mathbf{x}^{(i)})$ 를 Variational 파라미터와 생성 파라미터인 $\phi, \theta$ 에 대하여 미분하고 최적화하고 싶은데, 이 Lower Bound의 $\phi$ 에 대한 Gradient는 다소 복잡하다.
이러한 문제에 대한 일반적인 Monte Carlo Gradient Estimator는 아래와 같다.
그런데 이 Gradient Estimator는 굉장히 큰 분산을 갖고 있어서 우리의 목적에 적합하지 않다.
1.2.3. The SGVB estimator and AEVB algorithm
이 섹션에서는 Lower Bound의 실용적인 추정량과 파라미터에 대한 그 추정량의 미분 값을 소개할 것이다.
\[q_{\phi} (\mathbf{z}|\mathbf{x})\]일단 우리는 위와 같은 근사 Posterior를 가정한다. 다만 x에 대한 조건부를 가정하지 않은 케이스인 $q_{\phi}(\mathbf{z})$ 와 같은 경우에도 같은 테크닉을 적용할 수 있음에 유의하자. Posterior를 추론하는 Fully Variational Bayesian 방법론은 본 논문의 부록에 소개되어 있다.
위에서 설정한 근사 Posterior에 대해 1.2.4 섹션에서 정한 certain mild conditions 하에 우리는 그 근사 Posterior를 따르는 확률 변수 $\tilde{\mathbf{z}}$ 를 Reparameterize 할 수 있는데, 이는 Auxiliary Noise 변수 $\epsilon$ 의 Diffrentiable Transformation($g_{\phi} (\epsilon, \mathbf{x})$)를 통해 이루어진다.
다음 Chapter를 보면 적절한 $p(\epsilon)$ 분포와 $g_{\phi} (\epsilon, \mathbf{x})$ 함수를 선정하는 일반적인 방법에 대해 알 수 있다. 이제 이 Chapter 서두에서 언급한 근사 Posterior에 대해 어떤 함수 $f(\mathbf{z})$ 기댓값의 Monte Carlo 추정량을 다음과 같이 쓸 수 있다.
이는 실제로 계산하기 어려운 어떤 함수에 대해 $L$ 개의 Sample를 뽑아 이에 대한 근사치로 추정량을 구하는 방법이다.
이제 이 테크닉을 ELBO에 대해 적용하면 SGVB: Stochastic Gradient Variational Bayes 추정량을 얻을 수 있다.
\[\tilde{\mathcal{L}}^A (\theta, \phi ; \mathbf{x}^{(i)}) \simeq \mathcal{L} (\theta, \phi ; \mathbf{x}^{(i)})\] \[\tilde{\mathcal{L}}^A (\theta, \phi ; \mathbf{x}^{(i)}) = \frac{1}{L} \Sigma_{l=1}^L log p_{\theta} (\mathbf{x}^{(i)}, \mathbf{z}^{(i, l)}) - logq_{\phi} (\mathbf{z}^{(i, l)}|\mathbf{x}^{(i)})\] \[g_{\phi} (\epsilon^{(i, l)}, \mathbf{x}^{(i)}), \epsilon^{(l)} \sim p(\epsilon)\]잠시 아래 식에서 쿨백-라이블리 발산에 주목해보자.
\[\mathcal{L} (\theta, \phi; \mathbf{x}^{(i)}) = -D_{KL} (q_{\phi} (\mathbf{z}|\mathbf{x}^{(i)}) || p_{\theta} (\mathbf{z}) ) + E_{q_{\phi} (\mathbf{z} | \mathbf{x}^{(i)})} [log p_{\theta} (\mathbf{x}^{(i)} | \mathbf{z}) ]\]이 쿨백-라이블리 발산 값은 종종 analytic 하게 적분될 수 있는데 이렇게 되면 오직 Expected Reconstruction Error만이 샘플링에 의한 추정을 필요로하게 된다. Expected Reconstruction Error 항은 아래 식을 의미한다.
쿨백-라이블리 발산 항은 근사 Posterior를 Prior $p_{\theta}(z)$ 에 가깝게 만들어서 $\phi$ 를 규제하는 것으로 해석될 수 있다.
\[KL: q_{\phi} (\mathbf{z}|\mathbf{x}) \to p_{\theta}(\mathbf{z})\]이러한 과정을 SGVB 추정량의 두 번째 버전으로 이어지는데, 이 추정량은 일반적인 추정량에 비해 작은 분산을 갖고 있다.
\[\tilde{\mathcal{L}}^B (\theta, \phi ; \mathbf{x}^{(i)}) = -D_{KL} (q_{\phi} (\mathbf{z}|\mathbf{x}^{(i)}) || p_{\theta} (\mathbf{z}) ) + \frac{1}{L} \Sigma_{l=1}^L log p_{\theta} (\mathbf{x}^{(i)} | \mathbf{z}^{(i, l)})\]이 때
\[\mathbf{z}^{(i, l)} = g_{\phi} (\epsilon^{(i, l)}, \mathbf{x}^{(i)}), \epsilon^{(l)} \sim p(\epsilon)\]$N$ 개의 데이터 포인트를 갖고 있는 데이터셋 $X$ 에서 복수의 데이터 포인트가 주어졌을 때 우리는 미니배치에 기반하여 전체 데이터셋에 대한 Marginal Likelihood Lower Bound의 추정량을 구성할 수 있다.
\[\mathcal{L} (\theta, \phi ; X) \simeq \tilde{\mathcal{L}}^M (\theta, \phi ; X^M) = \frac{N}{M} \Sigma_{i=1}^M \tilde{\mathcal{L}} (\theta, \phi ; \mathbf{x}^{(i)})\]이 때
\[X^M = [\mathbf{x}^{i}]_{i=1}^M\]미니배치 $X^M$ 은 전체 데이터셋 $X$ 에서 랜덤하게 뽑힌 샘플들을 의미한다. 본 논문의 실험에서, 미니 배치 사이즈 $M$ 이 (예를 들어 100) 충분히 크면 데이터 포인트 별 sample의 크기인 $L$ 이 1로 설정될 수 있다는 사실을 알아 냈다.
\[\triangledown_{\theta, \phi} \tilde{\mathcal{L}} (\theta; X^M)\]위와 같은 derivate가 도출될 수 있고, 이에 따른 Gradients는 SGD나 Adagrad와 같은 확률적 최적화 방법과 연결되어 사용될 수 있다.
다음은 기본적인 Stochastic Gradients를 계산하는 방법에 대한 내용이다.

아래 목적 함수를 보면 Auto-Encoder와의 연결성이 더욱 뚜렷해진다.
\[\tilde{\mathcal{L}}^B (\theta, \phi ; \mathbf{x}^{(i)}) = -D_{KL} (q_{\phi} (\mathbf{z}|\mathbf{x}^{(i)}) || p_{\theta} (\mathbf{z}) ) + \frac{1}{L} \Sigma_{l=1}^L log p_{\theta} (\mathbf{x}^{(i)} | \mathbf{z}^{(i, l)})\]Prior로부터 나온 근사 Posterior에 대한 쿨백-라이블리 발산 값인 첫 번째 항은 Regularizer의 역할을 하며, 두 번째 항은 Expected Negative Reconstruction Error의 역할을 하게 된다.
$g_{\phi} (.)$ 라는 함수는 데이터 포인트 $\mathbf{x}^{(i)}$ 와 Random Noise Vector $\epsilon^{(l)}$ 을 데이터 포인트 $\mathbf{z}^{(i, l)}$ 을 위한 근사 Posterior로 부터 추출된 Sample로 매핑하는 역할을 수행한다.
\[\tilde{\mathbf{z}} = q_{\phi} (\mathbf{z}|\mathbf{x}), \tilde{\mathbf{z}} \sim g_{\phi} (\epsilon, \mathbf{x}), \epsilon \sim p(\epsilon)\]그 후, 이 Sample $\mathbf{z}^{(i, l)}$ 은 아래 함수의 Input이 된다.
\[log p_{\theta} (\mathbf{x}^{(i)} | \mathbf{z}^{(i, l)})\]이 함수는 $\mathbf{z}^{(i, l)}$ 이 주어졌을 때 생성 모델 하에서 데이터 포인트 $\mathbf{x}^{(i)}$ 의 확률 밀도 함수와 동일하다. 이 항은 Auto-Encoder 용어에서 Negative Reconstruction Error에 해당한다.
1.2.4. The Reparamaterization Trick
\[q_{\phi} (\mathbf{z}|\mathbf{x})\]위에 제시된 근사 Posterior로부터 Sample을 생성하기 위해 본 논문에서는 다른 방법을 적용하였다. 본질적인 Parameterization 트릭은 굉장히 단순하다. $\mathbf{z}$ 가 연속형 확률 변수이고 아래와 같이 어떤 조건부 분포를 따른다고 하자.
\[\mathbf{z} \sim q_{\phi} (\mathbf{z}|\mathbf{x})\]그렇다면 이제 이 확률 변수 $\mathbf{z}$ 를 다음과 같은 Deterministic 변수라고 표현할 수 있다.
이 때 $\epsilon$ 은 독립적인 Marginal $p(\epsilon)$ 을 가지는 보조 변수이고, $g_{\phi} (.)$ 함수는 $\phi$ 에 의해 parameterized 되는 vector-valued 함수이다.
이 Reparameterization은 매우 유용하다. 왜냐하면 근사 Posterior의 기댓값을 $\phi$에 대해 미분 가능한 기댓값의 Monte Carlo 추정량으로 재표현하는 데에 사용될 수 있기 때문이다.
증명은 다음과 같다. $z = g_{\phi} (\epsilon, \mathbf{x})$ 라는 Deterministic Mapping이 주어졌을 때 우리는 다음 사실을 알 수 있다.
이는 각 Density에 derivatives를 곱한 것이 서로 같다는 것을 의미한다. 참고로 위에서 $dz_i$ 라고 표기한 것은, 무한소에 대한 수식이기 때문이며 사실 $d\mathbf{z} = \prod_i dz_i$ 이다. 따라서 아래와 같은 식을 구성할 수 있다.
\[\int q_{\phi} (\mathbf{z}|\mathbf{x}) f(\mathbf{z}) d\mathbf{z} = \int p(\epsilon) f(\mathbf{z}) d\mathbf{z} = \int p(\epsilon) f(g_{\phi} (\epsilon, \mathbf{x}) ) d\epsilon\]마지막 식을 보면 $\mathbf{z}$ 를 Deterministic 하게 표현하여 오로지 $\epsilon, \mathbf{x}$ 로만 식을 구성한 것을 알 수 있다. 이제 미분 가능한 추정량을 구성할 수 있다.
사실 이는 이전 Chapter에서 ELBO의 미분 가능한 추정량을 얻기 위해 적용하였던 트릭이다.
예를 들어 단변량 정규분포의 케이스를 생각해보자.
\[z \sim p(z|x) = \mathcal{N} (\mu, \sigma^2)\]이 경우 적절한 Reparameterization은 $z = \mu + \sigma \epsilon$이다. 이 때 $\epsilon$은 $\mathcal{N} (0, 1)$을 따르는 보조 Noise 변수이다. 그러므로 우리는 다음 식을 얻을 수 있다.
그렇다면 어떤 근사 Posterior에 따라 미분 가능한 변환 함수 $g_{\phi}(.)$ 와 보조 변수 $\epsilon \sim p(\epsilon)$ 은 어떻게 선택하는가? 기본적인 방법은 다음과 같다.
첫 번째로, Tractable Inverse CDF를 선택한다. $\epsilon \sim \mathcal{U} (\mathbf{0}, \mathbf{I})$ 일 때, $g_{\phi} (\epsilon, \mathbf{x})$ 는 근사 Posterior의 Inverse CDF라고 해보자. 예를 들면, Exponential, Cauchy, Logistic, Rayleigh, Pareto, Weibull, Reciprocal, Gompertz, Gumbel, Erlang 분포가 있다.
두 번째로, 정규 분포 예시와 유사하게 어떠한 location-scale family of distributions에 대해 우리는 location=0, scale=1인 표준 분포를 보조 변수 $\epsilon$ 으로 선택할 수 있다.
그렇다면 $g(.)$ = location + scale * $\epsilon$ 이 될 것이다. 예를 들면, Laplace, Elliptical, T, Logistic, Uniform, Triangular, Gaussian이 있다.
마지막으로 분포를 결합하는 방식을 채택할 수 있다. 종종 확률 변수를 보조 변수의 다른 변환으로 표현할 수 있다. 예를 들어 Log-Normal, Gamma, Dirichlet, Beta, Chi-Squared, F가 있다.
이 3가지 방법이 모두 통하지 않는다면, Inverse CDF의 좋은 근사법은 PDF에 비해 많은 연산량과 소요 시간을 요한다.
1.3. Example: Variational Auto-Encoder
이번 Chapter에서는 확률론적 Encoder (생성 모델의 Posterior의 근사) 와 AEVB 알고리즘을 통해 파라미터 $\phi$ 와 $\theta$ 가 Jointly 최적화되는 신경망에 대한 예시를 다루도록 할 것이다.
잠재 변수에 대한 Prior는 Centered Isotropic Multivariate Gaussian $p_{\theta} (\mathbf{z}) = \mathcal{N} (\mathbf{z}; \mathbf{0}, \mathbf{I})$ 라고 하자. 이 경우에서는 Prior에 파라미터가 없다는 사실을 염두에 두자.
위 분포는 다변량 정규 분포 혹은 베르누이 분포(각각 실수 데이터, 또는 Binary 데이터 일때)로 설정하고, 분포의 파라미터는 Multi Layer Perceptron에서 $\mathbf{z}$ 로 계산된다.
\[p_{\theta} (\mathbf{z} | \mathbf{x}), q_{\phi} (\mathbf{z} | \mathbf{x})\]이 경우 위 식의 왼쪽 부분인 True Posterior는 intractable하다. 위 식의 오른쪽 부분인 근사 Posterior에 더 많은 자유가 있기 때문에, 우리는 True(but intractable) Posterior가 Approximately Diagonal Covariance를 가진 근사 정규분포를 따른다고 가정한다. 이 경우 우리는 Variational Approximate Posterior가 Diagonal Covariance 구조를 가진 다변량 정규분포라고 설정할 수 있다.
이 때 근사 Posterior의 평균과 표준편차는 MLP의 Output이다. 이 때 MLP는 Variational Parameter인 $\phi$ 와 데이터 포인트 $\mathbf{x}^{(i)}$ 의 비선형적 함수라고 생각할 수 있다.
1.2.4 에서 설명하였듯이, 우리는 다음과 같이 근사 Posterior에서 Sampling을 한다.
\[\mathbf{z}^{(i, l)} \sim q_{\phi} (\mathbf{z} | \mathbf{x}^{(i)})\]이 때 아래 사실을 이용한다.
\[\mathbf{z}^{(i, l)} = g_{\phi} (\mathbf{x}^{(i)} , {\epsilon}^{(l)} ) = {\mu}^{(i)} + {\sigma}^{(i)} \odot {\epsilon}^{(l)}, {\epsilon}^{(l)} \sim \mathcal{N} (\mathbf{0}, \mathbf{I})\]이 모델에서 Prior와 근사 Posterior는 정규 분포를 따른다. 그러므로 우리는 이전 Chapter에서 보았던 추정량을 사용할 수 있는데, 이 때 쿨백-라이블리 발산 값은 추정 없이 계산되고 미분될 수 있다.
\[\mathcal{L} (\theta, \phi, \mathbf{x}^{(i)}) \simeq \frac{1}{2} \Sigma_{j=1}^J (1 + log( (\sigma_j^{(i)})^2 ) - (\mu_j^{(i)})^2 - (\sigma_j^{(i)})^2 ) + \frac{1}{L} \Sigma_{l=1}^L log p_{\theta} (\mathbf{x}^{(i)} | \mathbf{z}^{(i, l)})\]이 때
\[\mathbf{z}^{(i, l)} = g_{\phi} (\mathbf{x}^{(i)} , {\epsilon}^{(l)} ) = {\mu}^{(i)} + {\sigma}^{(i)} \odot {\epsilon}^{(l)}, {\epsilon}^{(l)} \sim \mathcal{N} (\mathbf{0}, \mathbf{I})\] \[log p_{\theta} (\mathbf{x}^{(i)}, \mathbf{z}^{(i, l)})\]바로 위에 있는 Decoding Term은 우리가 모델링하는 데이터의 종류에 따라 베르누이 또는 정규분포 MLP가 된다.
1.4. Related Work
Wake-Sleep 알고리즘은 연속적인 잠재 변수를 갖고 있는 같은 문제를 갖고 있는 상황에 적용할 수 있는 다른 방법론이다. 본 논문에서 제시된 방법과 마찬가지로 이 알고리즘은 True Posterior를 근사하기 위해 인식 모델을 사용한다. 그러나 이 이 알고리즘의 경우 동시에 발생하는 2개의 목적함수를 최적화해야 하기 때문에 Marginal Likelihood의 최적화에 적합하지 않다. 이 알고리즘은 이산적인 잠재변수를 다루는 모델에 적합하다. Wake-Sleep 알고리즘의 데이터 포인트 별 계산 복잡도는 AEVB와 같다.
Stochastic Variational Inference는 주목 받는 알고리즘이다. 이 논문에서는 2.1 장에서 Naive Gradient Estimator의 높은 분산을 감소시키기 위해 Control Variate Scheme을 소개하였고, 이를 Posterior의 Exponential Family Approximation에 적용하였다.
AEVB 알고리즘은 Variational Objective로 학습되는 Directed Probabilistic Model과 Auto-Encoder 사이의 연결성을 밝혀준다. 선형적인 Auto-Encoder와 Generative Linear-Gaussian 모델의 특정 종류 사이의 연결성은 오래 전부터 알려져왔다. 이 논문은 PCA가 아래 조건에 해당하는 Linear-Gaussian Model의 Maximum Likelihood라는 점을 밝히고 있다. (특히 매우 작은 $\epsilon$ 일 때)
Auto-Encoder와 관련된 연구 중에서 이 논문은 unregularized auto-encoder는 input $X$ 와 잠재 표현 $Z$ 의 Mutual Information의 Maximum Lower Bound라는 것을 보였다. Mutual Information을 최대화하는 것은 결국 조건부 엔트로피를 최대화하는 것과 같은데, 이 조건부 엔트로피는 autoencoding 모델 하에서 데이터의 expected loglikelihood에 의해 lower bounded된다. (Negative Reconstruction Error)
그러나 이 Reconstruction 기준은 유용한 표현을 학습하기에는 sufficient하지 않다. denoising, contractive, sparse autoencoder 변인들이 Auto-Encoder로 하여금 더 유용한 표현을 학습하도록 제안되었다.
SGVB 목표함수는 Variational Bound에 의해 좌우되는 규제화 항을 포함하며, 일반적인 불필요한 규제화 하이퍼 파라미터들은 포함하지 않는다.
Predictive Sparse Decomposition과 같은 Encoder-Decoder 구조 역시 본 논문에서 영감을 받은 방법론이다. Generative Stochastic Network를 발표한 이 논문에서는 Noisy autoencoder가 데이터 분포로부터 Sampling을 하는 Markov Chain의 Transition Operator를 학습한다는 내용이 소개되어 있다. 다른 논문에서는 Deep Boltzmann 머신과 함께 인식 모델이 사용되기도 하였다. 이러한 방법들은 비정규화된 모델들에 타겟팅되어 있거나 희소 코딩 모델에 있어 제한적이며, 본 논문에서 제안된 알고리즘은 Directed Probabilisitic Model의 일반적인 경우를 학습할 수 있기 때문에 차별화 된다.
1.5. Experiments
(논문 참조)
1.6. Conclusion
본 논문에서 Variational Lower Bound의 새로운 추정량인 SGVB를 새롭게 소개하였다. 이 알고리즘은 연속적인 잠재 변수들에 대한 효율적인 근사적 추론을 가능하게 해준다. 제안된 추정량은 직접적으로 미분이 가능하고 표준적인 Stochastic Gradient 방법들을 사용하여 최적화될 수 있다.
iid 데이터셋과 연속적인 잠재 변수에 한해 본 논문에서는 효과적인 추론과 학습 방법인 AEVB: Auto-Encoding VB = VAE를 제안하였는데, 이 알고리즘은 SGVB 추정량을 사용하여 근사적인 추론을 행하는 모델이다. 이론적인 장점은 실험 결과에 반영되어 있다.
2. 보충 설명
2.1. VAE 요약
우리가 풀고 싶은 문제는 이것이다. 연속적인 잠재 변수가 존재한다고 할 때 데이터에 기반하여 이에 대한 효과적인 학습과 추론을 행하고 싶다. 그런데 문제가 존재한다.
\[p_{\theta} (\mathbf{x}), p_{\theta} (\mathbf{z} | \mathbf{x}), p_{\theta} (\mathbf{x} | \mathbf{z})\]위와 같은 Evidence, Posterior, Likelihood가 intractable한 경우가 매우 흔하게 존재한다. 그리고 데이터셋이 크다면 이들에 대해 배치 최적화나 Monte-Carlo Sampling을 통한 추론을 행하기에는 시간이 너무 오래 걸린다.
이를 위해 아래와 같은 새로운 인식 모델이 제안된다. 이 모델은 True Posterior를 근사하기 위해 제안되었으며 이러한 방법론을 Variational Inference 혹은 Variational Bayes라고 부른다.
기본적으로 ELBO를 최대화하는 $\theta, \phi$ 를 찾는 것으로 근사가 이루어진다.
\[\theta^*, \phi^* = argmax_{\theta, \phi} \Sigma_{i=1}^{N=1} \mathcal{L} (\theta, \phi ; \mathbf{x}^{(i)})\]최적화된 파라미터를 찾는 analytic한 전통적인 방법은 Coordinate Ascent Mean-Field Variational Inference이다. 글 서두에서도 밝혔듯이 이에 대한 내용은 이 글에서 확인할 수 있다. 이 방법은 여러 단점이 있는데, 그 중 하나는 factorial한 표현을 전제로 하기 때문에 본 논문에서와 같이 intractable한 Likelihood를 갖는 경우에는 사용이 불가능하다. 따라서 본 논문에서는 SGVB 추정량을 제안하고 있다.
SGVB는 파라미터의 Gradient를 구해 Stochastic하게 업데이트하는 방식을 취하는데, ELBO에서 $\phi$ 의 Gradient를 얻는 것은 다소 복잡하다. 따라서 Monte Carlo 추정량을 얻는 것을 생각할 수 있는데, 이 또한 분산이 너무 커서 직접적으로 사용하기에는 무리가 있다.
그래서 최종적으로 채택한 방법이 근사 Posterior를 따르는 확률 변수 $\tilde{\mathbf{z}}$ 에 대해 Reparameterization을 행하는 것이다. 근사 Posterior에서 직접 $\mathbf{z}$ 를 Sampling 하는 것이 아니라, 보조 Noise 변수 $\epsilon$ 을 사용하여 미분 가능한 분포에서 Deterministic하게 정해지는 것으로 파악하는 것이다.
기존의 ELBO는 아래와 같다.
\[\mathcal{L} (\theta, \phi; \mathbf{x}^{(i)}) = -D_{KL} (q_{\phi} (\mathbf{z}|\mathbf{x}^{(i)}) || p_{\theta} (\mathbf{z}) ) + E_{q_{\phi} (\mathbf{z} | \mathbf{x}^{(i)})} [log p_{\theta} (\mathbf{x}^{(i)} | \mathbf{z}) ]\]지금부터 2가지 케이스가 존재한다. 만약 첫 번째 항인 쿨백-라이블리 발산이 analytic하게 적분이 되지 않는다면 위 식 전체를 Monte-Carlo 추정을 통해 구해야 한다. 만약 가능하다면, 오직 두 번째 항만을 Monte-Carlo 추정을 통해 구하면 된다. (방금 전 분산이 커져서 사용하기 어렵다고 했던 부분은, $\mathbf{z}$ 를 근사 Posterior로부터 직접 Sampling을 할 때의 이야기이다.)
첫 번째 케이스(A)를 살펴보자. ELBO는 아래와 같이 다시 표현할 수 있다.
\[\mathcal{L}(\theta, \phi; \mathbf{x}^{(i)}) = E_{q_{\phi} (\mathbf{z}|\mathbf{x})} [-logq_{\phi}(\mathbf{z}|\mathbf{x}) + log p_{\theta}(\mathbf{x}, \mathbf{z})]\]그대로 Monte-Carlo 추정을 시행하면 아래와 같은 SGVB 추정량을 얻을 수 있다.
\[\mathcal{L} (\theta, \phi ; \mathbf{x}^{(i)}) \simeq \tilde{\mathcal{L}}^A (\theta, \phi ; \mathbf{x}^{(i)}) = \frac{1}{L} \Sigma_{l=1}^L log p_{\theta} (\mathbf{x}^{(i)}, \mathbf{z}^{(i, l)}) - logq_{\phi} (\mathbf{z}^{(i, l)}|\mathbf{x}^{(i)})\]이제 두 번째 케이스(B)를 살펴보자. 쿨백-라이블리 발산이 적분이 가능하다고 하였으므로, 두 번째 항인 Expected Reconstruction Error 만이 Sampling에 의한 Monte-Carlo 추정을 필요로 하게 된다. 참고로 첫 번째 항은 Regualizer의 역할을 수행한다.
이 때
\[\mathbf{z}^{(i, l)} = g_{\phi} (\epsilon^{(l)}, \mathbf{x}^{(i)}), \epsilon^{(l)} \sim p(\epsilon)\]$\mathbf{z}^{(i, l)}$ 은 위 목적 함수(SGVB-B)의 두 번째 항의 Input이다. 이 데이터 포인트는 $g_{\phi} (\epsilon^{(i)}, \mathbf{x}^{(i)})$ 에서 Sampling 되는 것이며 이 $g_{\phi} (.)$ 라는 함수는 일반적으로 일변량 정규분포로 설정된다. ($g_{\phi} (\epsilon, x) = \mu + \sigma \epsilon$) 이렇게 하면, 위 목적함수를 최적화하고 역전파를 이용하여 학습을 진행할 수 있게 된다.
2.2. Solution of Negative KL-Divergence
이전 Chapter에서 SGVB-B를 구할 때, 쿨백-라이블리 발산 값이 analytic하게 적분될 수 있는 경우를 가정하였다.
Prior와 근사 Posterior 모두 정규분포로 설정해보자.
\[p_{\theta} (\mathbf{z}) = \mathcal{N} (0, \mathbf{I}), q_{\phi} (\mathbf{z} | \mathbf{x}^{(i)}) \sim Normal\]$J$ 는 $\mathbf{z}$ 의 차원이라고 할 때, Negative 쿨백-라이블리 발산은 아래와 같이 정리할 수 있다.
\[-D_{KL} (q_{\phi} (\mathbf{z}|\mathbf{x}^{(i)}) || p_{\theta} (\mathbf{z}) ) = \int q_{\theta} (\mathbf{z}) (log p_{\theta}(\mathbf{z}) - log q_{\theta}(\mathbf{z}|\mathbf{x}^{(i)})) d\mathbf{z} = \frac{1}{2} \Sigma_{j=1}^J (1 + log( (\sigma_j^{(i)})^2 ) - (\mu_j^{(i)})^2 - (\sigma_j^{(i)})^2 )\]왜냐하면,
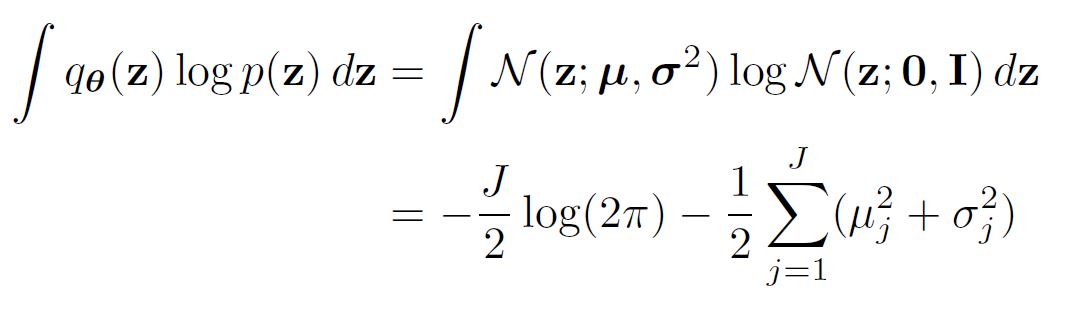
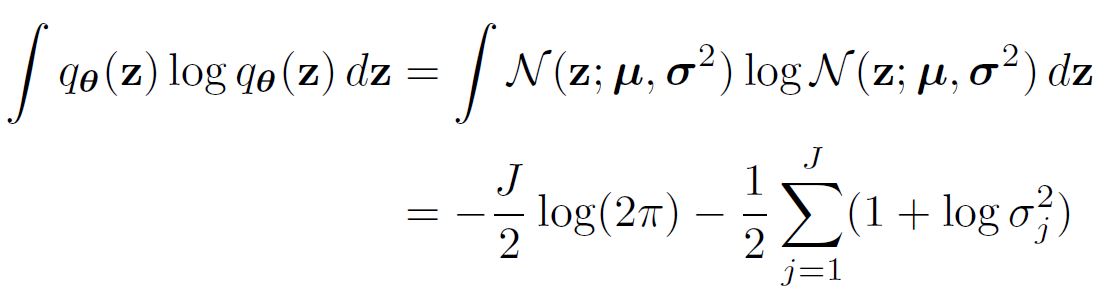
2.3. MLP’s as Probabilistic Encoders and Decoders
데이터의 종류에 따라 Decoder는 Gaussian Output을 반환할 수도, Bernoulli Output을 반환할 수도 있다. 두 경우 논문의 부록에 잘 설명되어 있다.
베르누이 분포일 경우
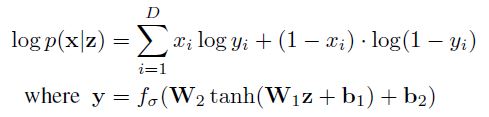
이 때 $f_{\sigma}(.)$ 함수는 elementwise sigmoid 활성화 함수이다.
정규 분포일 경우
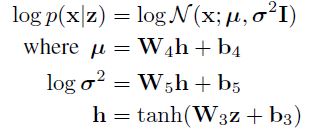
3. Tensorflow로 VAE 구현
Tensorflow 홈페이지에는 (흔히 그렇듯) MNIST 예제로 VAE를 적용하는 방법에 대해 가이드를 제시하고 있다. 코드도 깔끔하고 설명도 어느 정도 되어 있기 때문에 참고하기를 추천하며, 이번 Chapter 역시 그 가이드에 기반하여 작성되었음을 밝힌다. 다만 Tensorflow 홈페이지에서 제시한 예시는 SGVB-A를 사용하고 있는데, 본문을 읽어보면 단순한 예시를 들기 위해 ELBO 전체에 대해 Monte-Carlo 추정을 시행하였다고 밝히고 있다. 이번 Chapter에서는 SGVB-B를 활용하여 Loss Function을 설계할 것이다.
먼저 모델을 정의해보자.
class CVAE(tf.keras.Model):
def __init__(self, latent_dim):
super(CVAE, self).__init__()
self.latent_dim = latent_dim
self.encoder = tf.keras.Sequential(
[
tf.keras.layers.InputLayer(input_shape=(28, 28, 1)),
tf.keras.layers.Conv2D(filters=32, kernel_size=3, strides=(2, 2), activation='relu'),
tf.keras.layers.Conv2D(filters=64, kernel_size=3, strides=(2, 2), activation='relu'),
tf.keras.layers.Flatten(),
# No activation
tf.keras.layers.Dense(latent_dim + latent_dim),
])
self.decoder = tf.keras.Sequential(
[
tf.keras.layers.InputLayer(input_shape=(latent_dim, )),
tf.keras.layers.Dense(units=7*7*32, activation=tf.nn.relu),
tf.keras.layers.Reshape(target_shape=(7, 7, 32)),
tf.keras.layers.Conv2DTranspose(filters=64, kernel_size=3, strides=2, padding='same', activation='relu'),
tf.keras.layers.Conv2DTranspose(filters=32, kernel_size=3, strides=2, padding='same', activation='relu'),
# No activation
tf.keras.layers.Conv2DTranspose(filters=1, kernel_size=3, strides=1, padding='same'),
])
@tf.function
def sample(self, eps=None):
if eps is None:
eps = tf.random.normal(shape=(100, self.latent_dim))
return self.decode(eps, apply_sigmoid=True)
def encode(self, x):
# encoder의 Output은 (batch_size, latent_dim * 2) 이다.
# 각 mini-batch에서 이를 반으로 쪼갠다.
# logvar: Linear Layer를 통과한 후 음수의 값을 가질 수도 있기 때문에 이와 같이 표기한다.
mean, logvar = tf.split(self.encoder(x), num_or_size_splits=2, axis=1)
stddev = 1e-8 + tf.nn.softplus(logvar)
return mean, stddev
def reparameterize(self, mean, stddev):
# 보조 노이즈 변수: eps
eps = tf.random.normal(shape=mean.shape)
z = mean + eps * stddev
return z
def decode(self, z, apply_sigmoid=False):
logits = self.decoder(z)
if apply_sigmoid:
probs = tf.sigmoid(logits)
return probs
return logits
optimizer = tf.keras.optimizers.Adam(1e-4)
모델의 구조는 아래와 같은 그림으로 이해하면 쉬울 것이다.
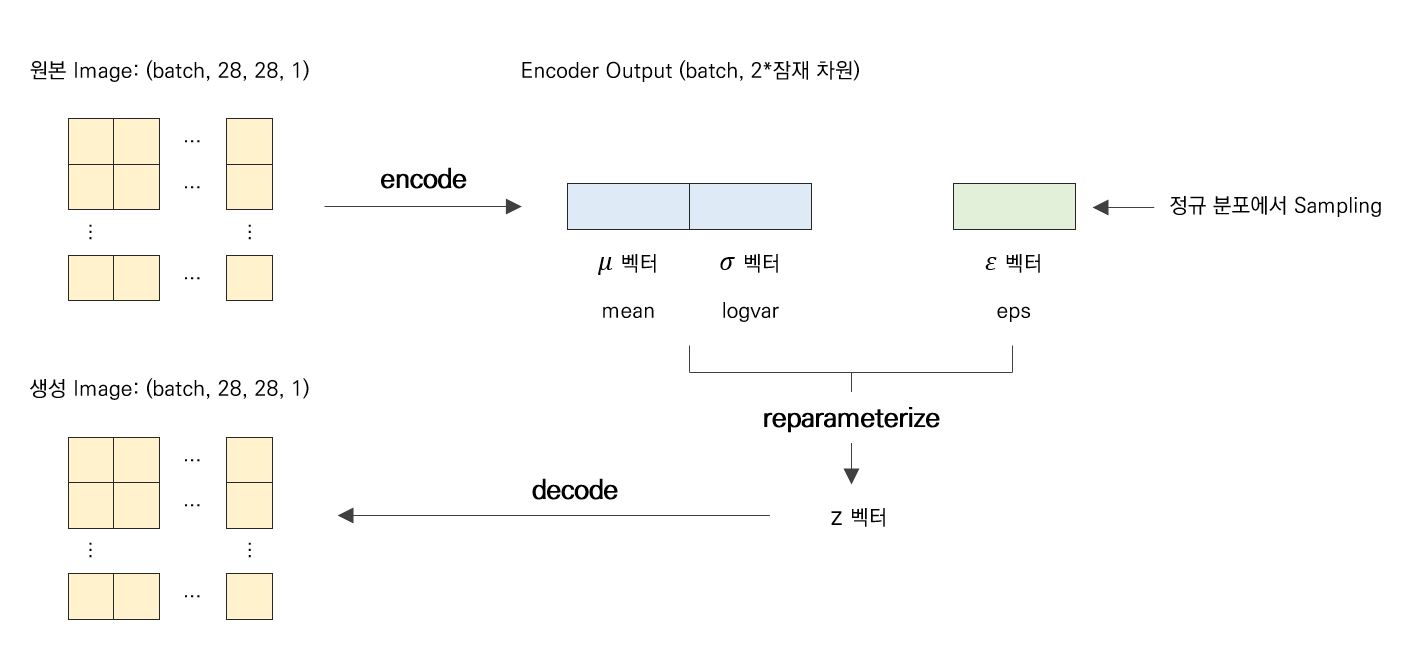
Prior와 근사 Posterior가 모두 정규 분포라는 가정 하에 Negative KL-Divergence는 아래와 같다.
그리고 2.3을 참고했을 때 다음과 같이 Log Likelihood를 얻을 수 있다.
\[logp_{\theta} (\mathbf{x}|\mathbf{z}) = \Sigma_{i=1}^{D} x_i log y_i + (1-x_i) * log(1 - y_i)\]자 그럼 이제 SGVB-B를 정확히 구해보자. ($J$ 는 잠재 변수의 차원이다.)
\[\tilde{\mathcal{L}}^B (\theta, \phi ; \mathbf{x}^{(i)}) = -D_{KL} (q_{\phi} (\mathbf{z}|\mathbf{x}^{(i)}) || p_{\theta} (\mathbf{z}) ) + \frac{1}{L} \Sigma_{l=1}^L log p_{\theta} (\mathbf{x}^{(i)} | \mathbf{z}^{(i, l)})\] \[= \frac{1}{2} \Sigma_{j=1}^J (1 + log( (\sigma_j^{(i)})^2 ) - (\mu_j^{(i)})^2 - (\sigma_j^{(i)})^2 ) + \frac{1}{L}\Sigma_{l=1}^L x_i log y_i + (1-x_i) * log(1 - y_i)\]이를 코드로 구현하면 아래와 같다.
def compute_loss(model, x):
mean, stddev = model.encode(x)
z = model.reparameterize(mean, stddev)
x_logit = model.decode(z, True)
x_logit = tf.clip_by_value(x_logit, 1e-8, 1-1e-8)
# Loss
marginal_likelihood = tf.reduce_sum(x * tf.math.log(x_logit) + (1 - x) * tf.math.log(1 - x_logit), axis=[1, 2])
loglikelihood = tf.reduce_mean(marginal_likelihood)
kl_divergence = -0.5 * tf.reduce_sum(1 + tf.math.log(1e-8 + tf.square(stddev)) - tf.square(mean) - tf.square(stddev),
axis=[1])
kl_divergence = tf.reduce_mean(kl_divergence)
ELBO = loglikelihood - kl_divergence
loss = -ELBO
return loss
학습 및 테스트 코드는 아래와 같다.
@tf.function
def train_step(model, x, optimizer):
with tf.GradientTape() as tape:
loss = compute_loss(model, x)
gradients = tape.gradient(loss, model.trainable_variables)
optimizer.apply_gradients(zip(gradients, model.trainable_variables))
return loss
epochs = 50
latent_dim = 2
model = CVAE(latent_dim)
# Train
for epoch in range(1, epochs + 1):
train_losses = []
for train_x in train_dataset:
loss = train_step(model, train_x, optimizer)
train_losses.append(loss)
print('Epoch: {}, Loss: {:.2f}'.format(epoch, np.mean(train_losses)))
# metric = tf.keras.metrics.Mean()
# for test_x in test_dataset:
# metric(compute_loss(model, test_x))
# elbo = -metric.result()
# Test
def generate_images(model, test_sample, random_sample=False):
mean, stddev = model.encode(test_sample)
z = model.reparameterize(mean, stddev)
if random_sample:
predictions = model.sample(z)
else:
predictions = model.decode(z, True)
predictions = tf.clip_by_value(predictions, 1e-8, 1 - 1e-8)
fig = plt.figure(figsize=(4, 4))
for i in range(predictions.shape[0]):
plt.subplot(4, 4, i + 1)
plt.imshow(predictions[i, :, :, 0], cmap='gray')
plt.axis('off')
plt.show()
num_examples_to_generate = 16
random_vector_for_generation = tf.random.normal(shape=[num_examples_to_generate, latent_dim])
test_sample = next(iter(test_dataset))[0:num_examples_to_generate, :, :, :]
for i in range(test_sample.shape[0]):
plt.subplot(4, 4, i + 1)
plt.imshow(test_sample[i, :, :, 0], cmap='gray')
plt.axis('off')
plt.show()
generate_images(model, test_sample, False)
실제로 학습을 시켜보면, Loss가 155까지는 빠르게 떨어지고, 그 이후에는 아주 서서히 감소하는 것을 알 수 있다. 이렇게 구현한 Convolutional VAE의 경우 성능은 좀 아쉽다. 아주 미세하게 숫자를 구분해 내지는 못한다. 아래의 이미지는 Epoch 30 이후의 결과이다.
원본

생성본
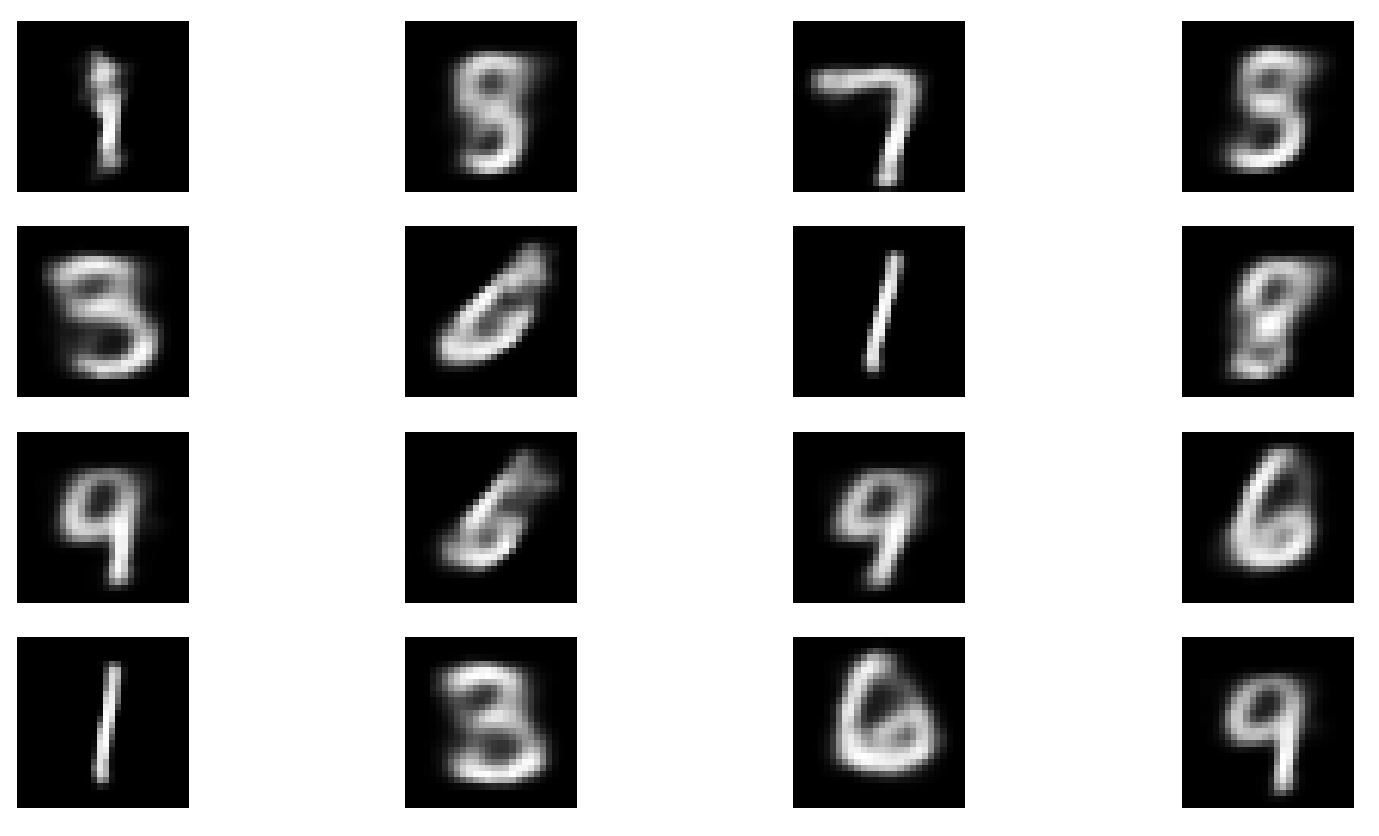
References
1) https://arxiv.org/abs/1312.6114
2) https://ratsgo.github.io/generative%20model/2018/01/27/VAE/
3) https://www.youtube.com/watch?v=SAfJz_uzaa8
4) https://taeu.github.io/paper/deeplearning-paper-vae/
5) https://dnddnjs.github.io/paper/2018/06/20/vae2/
6) https://www.tensorflow.org/tutorials/generative/cvae

