Gorio Tech Blog search

Bootstrap, Bagging, Boosting

06 Nov 2018 | Machine Learning Paper_Review

목차

Bootstrap: 부트스트랩의 개념

통계학에서의 부트스트랩과 기계학습에서의 부트스트랩은 그 의미가 다른 점도 있지만 본질적으로는 같다고 할 수 있다. 통계학적으로는 정확한 분포를 모르는 데이터의 통계치의 분포를 알아내기 위하여 Random Sampling을 하는 경우를 말하며, 종종 측정된 샘플이 부족한 경우에도 사용된다.
기계학습에서는 기본적으로 Random Sampling을 통해 데이터의 수를 늘리는 것을 말한다.

Decision Tree: 의사 결정 나무

내용을 입력합시당

Bagging: 배깅

Bagging은 Bootstrap Aggregatint의 줄임말이다. 특별히 부트스트랩이 over-fitting을 줄이는 데에 사용될 때를 말한다. 주어진 데이터에 대해 여러 번의 Random Sampling을 통해 Training Data를 추출하고 (여러 개의 부트스트랩을 생성), 독립된 모델로서 각각의 자료를 학습시키고 이를 앙상블로서 결합하여 최종적으로 하나의 예측 모형을 산출하는 방법이라고 할 수 있다.

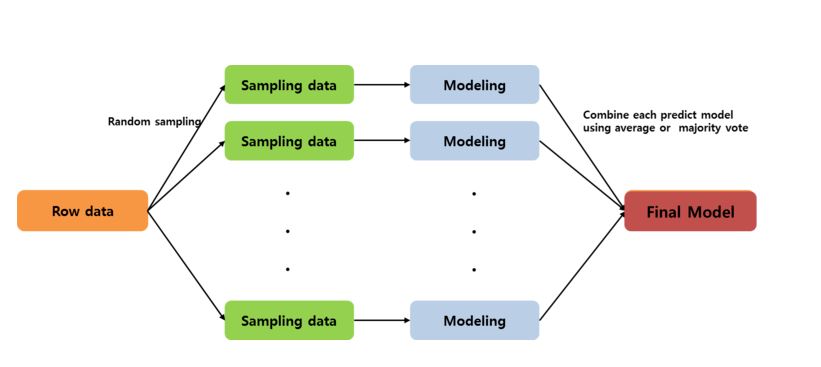
예를 들어 단일 Decision Tree는 변동성이 매우 크다. 이러한 단일 Decision Tree를 여러 개 결합하여 모델을 형성한다면 과적합을 방지할 수도 있고 안정된 결과를 산출할 수 있을 것이다.

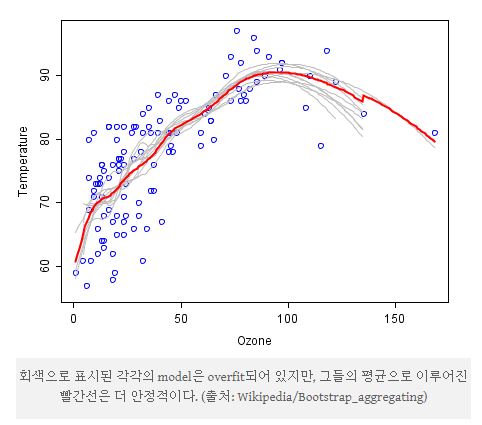
대표적인 예가 Random Forest이며, Sample의 예측변수들의 결합 시 Target Variable이 연속형일 때는 평균을, 범주형일 때는 다중 투표를 사용한다.

Boosting: 부스팅

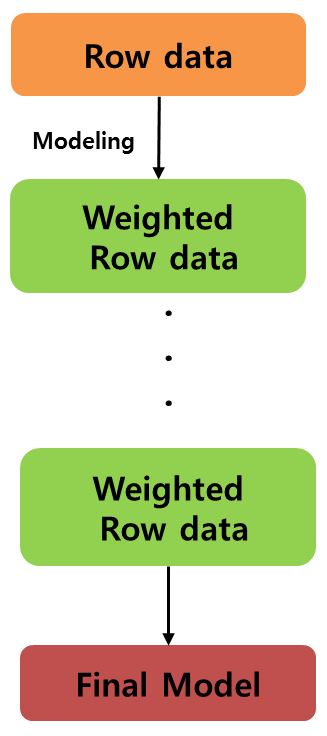
배깅이 독립적으로 모델을 학습시킨다면, 부스팅은 이전의 잘못을 파악하고 이를 이용하여 다음 번에는 더 나은 모델을 만들어 내자는 목표를 추구하면서 학습하는 방법이다. 분류 문제로 예를 들면, 잘못 분류된 개체들을 다음 번에는 더 잘 분류하고 싶은 것이 당연하다. 부스팅은 잘못 본류된 개체들에 집중하여 새로운 분류 규칙을 만드는 것을 반복하는 방법이며, 이는 결국 약한 예측모형들을 결합하여 강한 예측모형을 만드는 과정으로 서술할 수 있다.

XGBoost 이론

XGBoost는 Extreme Gradient Boosting의 줄임말로, 2014년에 등장하여 이후 지금까지 널리 쓰이고 있는 강력한 기계학습 알고리즘이다.
본 글에서는 XGBoost의 창시자인 Tianqi Chen과 Carlos Guestrin이 2016년 publish한
[XGBoost: A Scalable Tree Boosting System] 논문과 Chen의 관련 강연을 기초로 하여
알고리즘에 대해 설명하도록 하겠다.

알고리즘에 대한 설명이 끝난 이후에는 XGBoost Python의 메서드와 패키지의 주요 기능에 대해 알아본 뒤, Hyperparameter들을 튜닝하는 법에 대해 설명할 것이다.

XGBoost의 강점

  1. Regularization: 복잡한 모델에 대하여 페널티를 주는 Regularization 항이 있기 때문에 과적합을 방지할 수 있다.
  2. Handling Sparse Data: XGB는 원핫인코딩이나 결측값 등에 의해 발생한 Sparse Data(0이 많은 데이터) 또한 무리 없이 다룰 수 있다.
  3. Weighted Quantile Sketch: 가중치가 부여된 데이터 또한 Weighted Percentile Sketch 알고리즘을 통해 다룰 수 있다.
  4. Block Structure for parallel learning: 데이터는 정렬되어 in-memory units (blocks)에 저장된다. 이 데이터는 이후에 계속 반복적으로 재사용이 가능하기 때문에 다시 계산할 필요가 없다. 이를 통해 빠르게 Split Point를 찾아낼 수 있고 Column Sub-sampling을 진행할 수 있다.
  5. Cache Awarness: 하드웨어를 최적으로 사용하도록 고안되었다.
  6. Out-of-core computing: 거대한 데이터를 다룰 때 디스크 공간을 최적화하고 사용 가능 범위를 최대화한다.

[1] Regularized Learning Objective
n개의 example과 m개의 feature(변수)로 이루어진 데이터셋이 있다고 할 때,

\[D = {(x_i, y_i)} (|D| = n, x_i \in \mathbb{R^m}, y_i \in \mathbb{R})\]

앙상블 모델은 output을 예측하기 위해 K개의 additive functions(가법 함수)를 이용한다. 즉, f(x)는 q(x)라는 Tree 구조의 weight을 의미하는데,

$ \vec{x_i} $라는 i번째 데이터가 Input으로 들어왔을 때, 각각의 Tree가 Decision Rule을 통해 산출한 score = output = $ f_k(x_i) $ 을 모두 더한 값을 아래의 식과 같이 최종 output = $ \hat{y_i} $ 으로 출력하게 된다.

\[\hat{y_i} = \phi(\vec{x_i}) = \sum_{k=1}^K f_k(\vec{x_i}), f_k \in \mathbb{F}\] \[\mathbb{F} = \{ f(\vec{x}) = w_{q(x)} \} (q:\mathbb{R} \rightarrow T, w \in \mathbb{R}^T)\]

여기서 K는 Tree의 개수를, T는 Tree 안에 있는 leaf의 개수를, w는 leaf weights를, $ w_i $는 i번째 leaf의 score를 의미한다.
q는 example을 leaf index에 매핑하는 Tree 구조를 말하는데 이 안에는 물론 Tree 내부의 수많은 Decision Rule을 포함한다.
F는 모든 Regression Trees를 포함하는 space of functions를 의미하며,
여기서 Classification and Regression Trees의 경우 CART라고도 한다.

이러한 함수들을 학습하기 위해서는 다음과 같은 Objective Function을 상정할 필요가 있다.
아래의 Regularized Objective는 예측 값과 실제 값 사이의 차이와 Regularized Term으로 구성된다.

\[L(\phi) = \sum_{i}^{n} l(\hat{y_i}, y_i) + \sum_{k=1}^{K} \Omega(f_k)\]

여기서 $ \Omega(f) = \gamma T + \frac{1}{2} \lambda \Vert{w}\Vert^2 $

물론 위의 $ l $은 미분 가능한 convex loss function이 될 것이며,
간단한 예로는 Square Loss나 Log Loss를 생각할 수 있을 것이다.

오른쪽 부분인 $ \Omega $의 역할은 모델이 너무 복잡해지는 것을 막는 페널티 항이다.
이 항은 과적합을 방지하기 위해 final learnt weights을 부드럽게 만들어줄 것이다. (Smoothing)

항을 자세히 보면, Tree 개수가 너무 많아지거나 leaf weights의 L2 norm이 너무 커지면 전체 Loss를 증가시키는 것을 알 수 있다.

[2] Gradient Tree Boosting
위에서 본 전체 Loss는 각각의 Tree 구조 자체( f(x) )를 포함하고 있기 때문에 최적화하기가 까다롭다. 따라서 아래의 방법으로 최적화 과정에 논의해볼 것이다.

일단 $ \hat{y_i}^{(t)} $를 t번 째 iteration(t번 째 Tree)에서의 i번 째 Instance(실제 개체)의 예측 값이라고 해보자,

이 값은 아래의 과정에 의해 표현될 수 있다.

\(\hat{y_i}^{(0)} = 0\)
\(\hat{y_i}^{(1)} = f_1(x_i) + \hat{y_i}^{(0)}\)
\(...\)
\(\hat{y_i}^{(t)} = \sum_{k=1}^{t} f_k(x_i)\)

따라서 전체 Loss를 아래와 같이 표현할 수 있다.

\[L^{(t)} = \sum_{i=1}^{n} l({y_i}, \hat{y_i}^{(t-1)} + f_t(\vec{x_i})) + \Omega(f_t)\]

이 단계에서 위의 $ l $ 부분을 2차항까지 사용한 테일러 전개에 의해 근사적으로 구하면, 다시 아래와 같이 표현할 수 있다.

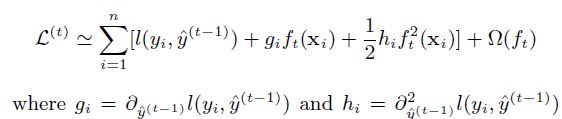
예를 들어 $ l $을 Square Loss로 사용하였다면, 아래와 같은 전개가 가능할 것이다.

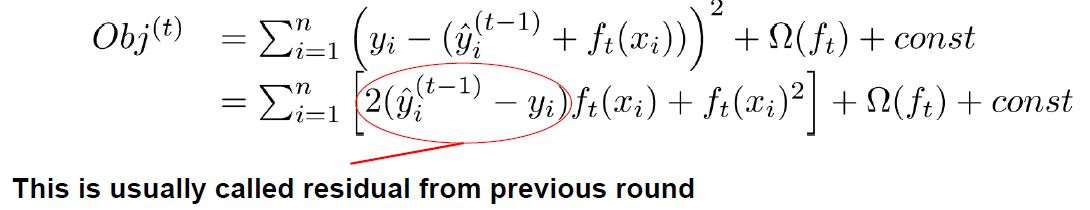
일반화된 식으로 다시 보면 상수항을 제거하고 남은 step t에서의 근사한 전체 Loss는 아래와 같다.

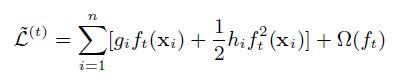
여기서 잠시 $ I_j = {i|q(\vec{x_i} = j)} $를
instance set of leaf j (leaf j의 할당 결과물)이라고 정의하겠다.

위의 식에서 정규화 항을 확장하여 정리해보면,

\[\tilde{L}^{(t)} = \sum_{i=1}^{n} [g_i f_i(\vec{x_i}) + \frac{1}{2}h_i f_t^2(\vec{x_i})] + \gamma T + \frac{1}{2} \sum_{j=1}^{T} w_j^2\] \[= \sum_{i=1}^{n} [g_i w_q(\vec{x_i}) + \frac{1}{2}h_i w_q^2(\vec{x_i})] + \gamma T + \frac{1}{2} \sum_{j=1}^{T} w_j^2\]

example 단위에서 leaf 단위로 식을 재표현해주면,

\[= \sum_{j=1}^{T} [ (\sum_{i \in I_j} g_i)w_j + \frac{1}{2} (\sum_{i \in I_j} h_i + \lambda) w_j^2 ] + \gamma T\]

식을 보기 좋게 표현하기 위해 아래와 같은 정의를 사용하겠다.

\[G_j = \sum_{i \in I_j} g_i, H_j = \sum_{i \in I_j} h_i\]

고정된 $ q(\vec{x}) $에 대하여 위의 식 = 0으로 놓고 계산하면,
leaf j의 최적 weight을 계산할 수 있다.

\[w_j^* = - \frac{G_j} {H_j + \lambda}\]

이 때의 전체 Loss는 아래와 같다.

\[\tilde{L}^{(t)}(q) = - \frac{1}{2} \sum_{j=1}^{T} \frac{G_{j}^2} {H_j + \lambda} + \gamma T\]

정리하자면, 위의 식은 사실상 q라는 Tree 구조의 성능(quality)을 측정하는 Scoring Function의 역할을 수행하게 된다. 이 Score는 Decision Tree에서의 불순도와 같은 역할을 한다.

그런데 다만 여기서 생각해야 할 점은, 발생가능한 수많은 Tree의 구조를 일일히 다 평가할 수는 없다는 것이다. 이를 위해 Greedy 알고리즘이 사용되는데, 이 알고리즘은 단일 Leaf에서 시작하여 가지를 반복적으로 확장해 나가는 방법을 말한다.

$ I_L, I_R $을 각각 split 이후의 좌측, 우측 노드의 Instance Sets라고 할 때,
Gain 혹은 Loss reduction이라고 불리는 아래의 식은,

\[Gain = L_{split} = \frac{1}{2} [ \frac{G_{L}^2} {H_L + \lambda} + \frac{G_{R}^2} {H_R + \lambda} - \frac{ (G_{L} + G_{R})^2 } {H_L + H_R + \lambda} ] - \gamma\]

Left Child의 스코어 + Right Child의 스코어 - Split 안했을 때의 스코어 - Complexity cost by introducing additional leaf로 표현된다.

이는, split을 했을 때의 이득 (loss reduction)이 $ \gamma $로 표현되는 어떤 상수보다 작으면, split을 하지 말라는 뜻이다.
즉, Training Loss Reduction < Regularization Constant라면 split을 중지하게 되며,
이는 Pruning 시스템이라고 할 수 있다.

Pruning에는 2가지 방법이 있다.

  1. Pre-Stopping: Best Split이 음수 Gain을 가지면 Stop한다. 다만 Future Split에서의 이득을 고려하지 못하므로 주의가 요구된다.
  2. Post-Pruning: Max_depth까지 확자한 후에 Negative Gain을 가진 Split 모두를 가지치기 한다.

[3] Efficient Findings of the Best Split

Exact Greedy Algorithm에서는 데이터를 Feature Value에 따라 정렬한 후 이와 같은 Gain을 반복적으로 계산하여 가장 높은 Gain을 바탕으로 Split을 결정하게 된다.
(In order to do so efficiently, the algorithm must first sort the data according to feature values and visit the data in sorted order to accumulate the gradient statistics for the structure score)
(자세한 내용은 논문을 참고할 것)

Approximate Algorithm에서는 적절한 Split 후보들을 선정한 후 그 중에서만 찾게 된다.

직관적으로는 다음과 같은 과정을 거친다고 말할 수 있다.

  1. Split할 양 쪽의 g, h의 합을 계산하는 것
  2. 정렬된 Instances(개체)를 left -> right 방향으로 스캔하면 feature 속에서 best split을 결정하기에 충분하다.

[3] Shrinkage and Colums Subsampling
위에서 설명된 정규화 과정 외에도 추가적으로 과적합을 막기 위한 방법이 도입된다.

Shrinkage는 Tree Boosting의 각 단계를 실행한 이후 $ \eta $라는 factor를 도입하여 새로 추가된 weight을 스케일링해주는 기법이다. tochastic optimization과 유사한 방법인데, shrinkage는 모델을 향상시키기 위해 각각의 개별 Tree와 미래의 Tree의 leaves space의 영향력을 감소시킨다.

Column(Feature) Subsampling은 Random Forest에서도 사용된 기법이다. 이 기법은 전통적인 Row- subsampling에 비해 더욱 효과적이고 빠르다고 알려져 있다.

[4] Weighted Quantile Sketch
위에서 언급하였듯이 근사 알고리즘에서는 후보 Split을 제안하는데, 보통 이 때 feature의 percentil은 후보들이 데이터 상에서 고르게 분포하도록 만든다.
그런데 XGBoost는 가중치가 부여된 데이터에 대해서도 효과적인 Handling이 가능하다.
(Weighted quantile sketch algorithm can handle weighted data with a provable theoretical guarantee)

논문의 4페이지를 살펴보면, Rank Function과 전체 Loss 식의 재표현을 통해서 위의 설명을 간단히 증명하고 있다.

[5] Sparsity-aware Split Finding
현실에서 데이터를 다룰 때 직면하게 되는 가장 큰 문제는 input인 $ \vec{x} $가 매우 sparse하다는 것이다. 이 현상에는 대표적으로 3가지 원인이 있다.

  1. 결측값
  2. 통계학에서의 빈번한 zero entries
  3. 원 핫 인코딩

XGB는 내재적으로 이러한 현상을 효과적으로 Handling할 수 있다.
왜냐하면 데이터를 통해 Optimal Default Direction이 학습되기 때문이다.

[6] System Design
글의 서두에서 언급하였는데, 하드웨어 측면에서도 XGB는 우수한 성능을 보인다.

  • Block Structure for parallel learning: 데이터는 정렬되어 in-memory units (blocks)에 저장된다. 이 데이터는 이후에 계속 반복적으로 재사용이 가능하기 때문에 다시 계산할 필요가 없다. 이를 통해 빠르게 Split Point를 찾아낼 수 있고 Column Sub-sampling을 진행할 수 있다.
  • Cache Awarness: 하드웨어를 최적으로 사용하도록 고안되었다.
  • Out-of-core computing: 거대한 데이터를 다룰 때 디스크 공간을 최적화하고 사용 가능 범위를 최대화한다.

XGB는 또한 Early Stopping 기능도 갖고 있다.
XGb는 참고로 Feature Engineering이나 Hyper Parameter 자동 튜닝 등의 기능은 갖고 있지 못하다.

이로써 XGBoost의 이론적 배경에 대해 살펴보았다.

XGBoost 패키지 Methods

지금부터는 XGBoost Python을 효과적을 Implement하는 방법에 대해 설명한다.

XGBoost Parameter Tuning

파라미터 튜닝의 세부사항을 설명하기 전에, 가장 전반적인 2가지 사항에 대해 설명한다.

  1. Control Overfitting
    일차적으로는 모델 Complexity를 직접적으로 조절할 수 있는데, 이는 max_depth, min_child_weight, gamma 파라미터 조정에 해당한다.

이후에 학습 과정을 Noise에 Robust하게 만들기 위해 Randomness를 추가하는 방법이 있는데, 이는 subsample, colsample_bytree 파라미터 조정에 해당한다.
또는 stepsize eta를 줄일 수도 있는데, 이 때는 num_round를 늘려야만 한다.

link: [https://xgboost.readthedocs.io/en/latest/tutorials/param_tuning.html]

  1. Handle Imbalanced Dataset
    불균형 데이터를 효과적으로 다루기 위해서는 scale_pos_weight 파라미터 조정을 통해 positive & negative weights를 균형적으로 맞출 수 있다.

만약 오직 right probability를 예측하는 것에만 관심이 있다면,
Dataset을 균형적으로 맞추기 힘드므로, max_delta_step 파라미터를 1과 같은 유한 실수로 세팅하면 효과적인 convergence(수렴)을 가능하게 할 수 있다.

XGBoost Parameters

XGB 파라미터는 크게 3가지로 구분된다.

  • General, Booster, Task paramers

General Parameters는 부스팅을 위해 어떤 부스터를 쓰는지와 관련이 있다.
Booster Parameters는 선택한 Booster에 의존한다.
Task Paramters는 학습 시나리오를 결정한다. 예를 들어, Regression tasks는 ranking tasks와 관련하여 다른 파라미터를 사용할 수 있다.

참고로 R에서는 _대신 .를 사용하면 된다.

1. General Parameters

  • booster [default=gbtree]
    gbtree(기본값), gblinear(선형), dart(tee based model 사용)

  • silent [default=0]
    0은 학습 과정을 출력해라, 1은 출력하지 마라.

  • nthread [default=최대치]
    XGB를 돌리기 위해 사용될 병렬 스레드의 개수

  • disable_default_eval_metric [default=0]
    flag to disable default metric. Set to >0 to disable

  • num_pbuffer, num_feature는 자동적으로 설정됨

2. Booster Parameters

  • eta [default=0.3, alias=learning_rate]
    과적합을 방지하기 위해 업데이트 과정에서 사용되는 shrinkage의 step size이다. 각 부스팅 단계이후 우리는 새로운 features에 대한 weights를 얻을 수 있는데, eta는 부스팅 과정을 더욱 보수적으로 만들기 위해 feature weights를 축소한다. 결론적으로 과적합을 방지하는 파라미터다!

  • gamma [default=0, alias=min_split_loss]
    Tree의 leaf split을 진행하기 위해 필요한 최소 Loss Reduction을 뜻한다.
    gamma가 커질수록, 알고리즘은 더욱 보수적으로 만들어질 것이다.
    min_loss_reduction이라는 다른 이름을 생각해볼 때, 이 파라미터는 아래의 식에서 $ \gamma $를 뜻한다.

\[Gain = L_{split} = \frac{1}{2} [ \frac{G_{L}^2} {H_L + \lambda} + \frac{G_{R}^2} {H_R + \lambda} - \frac{ (G_{L} + G_{R})^2 } {H_L + H_R + \lambda} ] - \gamma\]

  • max_depth [default=6]
    Tree구조의 최대 깊이이다. 0을 입력하면 한계치를 설정하지 않음을 뜻한다.

  • min_child_weight [default=1]
    Child Node에 필요한 Instance weight(hessian)의 최소합.
    만약 Tree의 Split 과정이 진행되면서 instance weight의 합이 min_child_weight보다 작은 leaf node가 나타난다면, Tree는 계속해서 Split을 진행하도록 설정하는 것이다.
    결론적으로 min_child_weight가 커질수록, 알고리즘은 더욱 보수적으로 변화한다.

  • max_delta_step [default=0]
    Maximum delta step we allow each leaf output to be.
    디폴트로 설정된 0은 제한이 없음을 뜻한다.
    양수로 설정이 되면, update step을 더욱 보수적으로 만들어준다.
    일반적으로 이 파라미터는 불필요한데, Logistic Regression에서 데이터셋이 심각하게 불균형한 경우 [1-10]에 해당하는 값을 설정한다면 도움이 될 수도 있다.

  • subsample [default=1]
    Training Instances의 Subsample 비율을 말한다.
    예를 들어 0.5로 설정될 경우, XGB가 학습 데이터의 절반을 랜덤하게 샘플링한다는 것을 뜻한다. Dropout과 유사한 측면이 있다.
    수치가 작아질 수록 과적합을 방지하지만 학습이 더뎌질 수 있다.

  • colsample_bytree [default=1]
    Subsample ratio of columns when constructing each tree.

  • colsample_bylevel [default=1]
    Subsample ratio of columns for each split, in each level.

  • lambda [default=1, alias:reg_lambda]
    Weight에 대한 L2 정규화항. 커질수록 모델을 보수적으로 만든다.

\[L(\phi) = \sum_{i}^{n} l(\hat{y_i}, y_i) + \sum_{k=1}^{K} \Omega(f_k) \leftarrow \Omega(f) = \gamma T + \frac{1}{2} \lambda \Vert{w}\Vert^2\]

  • alpha [default=0, alias: reg_alpha]
    Weight에 대한 L1 정규화항.

  • tree_method [defaul=auto]
    Tree 구성 구조 방법을 말한다. 단, Distributed and external memory 버전은 오직 approx만 지원한다.
    auto외에는 exact(Exact Greedy 알고리즘), approx(Approximate Greedy 알고리즘), hist(Fast Histo Optimized Approxmate Greedy 알고리즘), gpu_exact, gpu_hist 등이 있다.
    auto로 두면 적당한 크기의 데이터셋에 대해서는 exact를 선택하고, 데이터셋이 매우 커지면 approx를 자동으로 선택한다.
    이 방법들에 대한 간략한 설명은 위 논문 리뷰에서 다루었다.

  • scale_pos_weight [default=1]
    positive & negative weights의 밸런스를 조정하므로, 불균형 데이터에 대해 유용한 파라미터이다.

3. Task Parameters

  • objective [default=reg:linear]
    reg:linear, reg:logistic, binary:logistic, binary:logitraw, binary:hinge 위의 것에서 gpu:추가 가능
    count:poisson, survival:cos, multi:softmax, multi:softprob, rank:pairwise, rank:ndcg, rank:map, reg:gamma

  • base_score [default=0.5]
    The initial prediction score of all instances, global bias.
    바꿀 필요 없다.

  • eval_metric
    rmse, mae, logloss, error, auc, mlogloss, …

  • seed

Dart Booster이나 Linear Booster를 선택하였을 때 따라오는 추가적인 파라미터 조정은 Documentation을 참조할 것.
Console에서만 사용가능한 Line Parameter들도 있다.
Link: [https://xgboost.readthedocs.io/en/latest/parameter.html]

AdaBoost

AdaBoost는 Additive Boosting의 줄임말로, 1995년에 등장하였지만 빠르고 정확한 성능으로 좋은 평가를 받고 있는 알고리즘이다.
간결한 설명을 위해 본 논문의 설명은 m개의 training data에 대하여 Y는 = {-1, +1}로,
Binary Classification 문제로 범위를 제한한다.

AdaBoost는 t개의 weak(base) learning algorithm을 반복적으로 호출하여 학습을 진행한다. (t = 1 ~ T)

여기서 t번 째 round에서의 training example i에 대한 weight distribution을 $ D_t(i) $이라고 하자.

초기에 weight은 균일 분포로서 초기화되어 모두 동일하게 설정되지만,
잘못 분류된 example에 대한 weights는 증가하게 된다. 이렇게 되면 weak learner가 다음 round에서 학습을 진행할 때 이러한 example에 대해 더욱 집중하게 하는 효과를 낼 수 있다.

Weak Learner의 일은 $ D_t $ 분포에 적합한 weak hypothesis $ h_t : X \rightarrow {-1, +1} $을 찾는 것이다.
Weak Learner는 $ D_t $를 다시 학습할 때 사용하거나 $ D_t $에 따라 다시 표본이 추출될 수 있다.
그 weak hypothesis의 성능은 다음과 같이 Error를 계산하여 평가할 수 있다.

\[\epsilon_t = P_{i \sim D_t} [ h_t(x_i) \neq y_i] = \sum_{i:h_t(x_i) \neq y_i} D_t(i)\]

Adaboost의 부스팅 알고리즘은 아래와 같다. 사실 그리 어렵지는 않다.

$ \alpha_t $는 결국 $ h_t $에 배정된 가중치라고 볼 수 있다.

Analyzing the training error
$ \gamma_t $를 모델의 예측이 Random Guess보다 얼마나 나은지를 나타낸다고 하면,
$ h_t $의 Error인 $ \epsilon_t $은 $ \frac{1}{2} - \gamma_t $로 표현할 수 있다.

아래 식은, 최종 hypothesis H의 Training Error는 일정 수치보다 작을 수 밖에 없음을 나타내는데,
이는 만약 Weak Hypothesis가 적어도 Random Guess보다는 낫다면, 결과적으로 Training Error는 지수적으로 빠르게 감소할 수 밖에 없음을 나타낸다.

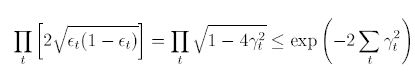
이전 알고리즘들도 이와 유사한 과정을 거쳤지만 이들은 $ \gamma_t $의 하한선인 $ \gamma $라는 상수에 대한 사전 정의가 필요했다. AdaBoost는 그러한 과정이 필요 없으며, 각각의 Weak Hypothesis의 Error rates에 adapt하는 모습을 보여준다.
이 때문에 AdaBoost는 Adaptive Boosting이다.

Generalization Error
기존의 연구는 최종 Hypothesis의 Generalization에러를 Training Error의 관점에서 설명할 때,
아래와 같은 식으로 나타냈었는데, 이는 T가 커질 때, boosting 모델은 결국 과적합한다는 것을 의미한다.

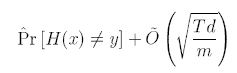
Sign Description
T boosting round 수
d hypotheseis의 공간의 compexity의 standard measure인 VC-차원
m example 수
$ \hat{Pr(.)} $ empirical probability on the training example

그런데 이후의 연구를 보면 이는 종종 사실이 아닌 것으로 나타났다.
특히 AdaBoost의 경우 Training Error가 0에 도달한 이후에 지속적인 학습을 진행한 결과,
(Generalization Error)Test Error가 점차적으로 감소한 것을 알 수 있었다.

이를 설명하기 위해 다른 개념이 도입되었는데, 아래를 Maring of exmaple(x, y)라고 한다.

\[{Margin} = \frac{y * \sum_t \alpha_t h_t(x)} {\sum_t \alpha_t}\]

이 식은 [-1, +1]에 속하며 H가 example을 적절히 분류했을 때 0의 값을 가진다.
이 Margin의 Magnitude는 prediction의 confidence를 측정한다고 해석할 수 있다.

이후에 증명된 바에 따르면,
Training Set에서 Margin이 더욱 증가하면 이는 Generalization Error의 상위의 상한선으로 변환된다고 한다.

식으로 표현하면 아래와 같은데, $ \theta $로 표현되는 상한선(Upper Bound)가 클 수록 Prediction에 자신이 있다는 뜻이고, 이 $ \theta $는 T에 독립적이기 때문에 반복 횟수가 증가해도 Error가 증가하지 않는다.

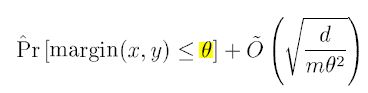
AdaBoost의 이와 같은 기재는 game-theoretic setting과 같은 방식으로도 이해될 수 있다.
이는 Boosting이 어떤 특정 게임의 반복 play라고 할 때,
AdaBoost는 이 게임에 반복적으로 참여하여 근사적으로 게임을 푸는 General한 알고리즘의 특별한 케이스라고 해석하는 것이다.

Experimetns and Applications

  1. AdaBoost는 간단하고 사용하기 쉽다. weak learner에 대한 사전지식이 필요없으며 여러 method와 결합하여 사용이 가능하다.
  2. T 빼고는 튜닝할 Hyperparameter가 없다.
  3. Noise에 민감하다.
  4. AdaBoost의 operation은 선형 번류기의 coordinate-wise gradient descent로 해석할 수 있다.
  5. AdaBoost는 Outlier를 찾아내는 데에 뛰어난 성능을 보인다. (높은 Weight은 Outlier일 확률이 높다.)

Related Posts