2019 ICML Papers(ICML 2019 논문 설명)
11 Jul 2019 | ICML목차
- Training Neural Networks with Local Error Signals
- Rates of Convergence for Sparse Variational Gaussian Process Regression
- Training Neural Networks with Local Error Signals
이 글에서는 2019년 ICML(International Conference on Machine Learning)에서 어떤 논문들이 accept되어 발표되었는지를 알아볼 것이다. 3424개의 논문이 접수되어 774개의 논문만이 구두 및 포스터 발표로 진행되었다.
논문 리스트는 목차와 같다. 774개를 다 살펴볼 수는 없으므로 몇 개만 추려서 최근 동향을 살펴보도록 하자.
Training Neural Networks with Local Error Signals
| 개요 | 내용 |
|---|---|
| 저자 | Francesco Locatello et al. Google Research |
| 논문 링크 | https://arxiv.org/abs/1811.12359 |
| 블로그 | https://ai.googleblog.com/2019/04/evaluating-unsupervised-learning-of.html |
| 제출일 | Submitted on 29 Nov 2018 (v1), last revised 18 Jun 2019 (this version, v4) |
이 논문은 표현(representation)에 대한 것인데, 논문에 쓰인 표현들이 참 어렵다.
초록을 대략 번역하자면,
풀린 표현(disentangled representation)의 무감독 학습(unsupervised learning)의 핵심 아이디어는 ‘실제 세계의 데이터는 무감독 학습 알고리즘에 의해 복구될 수 있는 몇 가지 설명요인에 의해 생성된다’는 것이다.
이 논문에서, 풀린 표현의 무감독 학습은 모델과 데이터 모두에 대해 귀납적 편향(inductive biases) 없이는 본질적으로 불가능하다는 것을 이론적으로 보일 것이다. 또한 6개의 최신 무감독 풀림 학습(unsupervised disentangled learning) 방법과 풀림 측정방식(disentangled measures)을 구현하여 이를 여러 데이터셋에 대해 12000개 이상의 모델을 학습시킬 것이다.
이로써
- 여러 방법들이 ‘대응되는 loss에 의한’ 성질들을 강제함에도 불구하고 감독 없이는 잘 풀린(well-disentangled) 모델은 식별될 수 없다는 사실과(역자 주: 모델이 식별될 수 없다는 것은 이를테면 두 가지 모델이 생성한 각각의 결과가 있을 때, 그 결과만 보고 원래 모델이 무엇이었을지를 알 수 없다는 뜻이다),
- ‘풀린 정도가 증가한(increased disentanglement)’ 것도 downstream task의 학습의 샘플 복잡도의 감소로 이어지지는 않는다는 것
을 알아내었다.
이같은 결과는 앞으로 풀린 학습에 대한 연구는
- 명백히 귀납적 편향과 감독에 의해야 하며,
- 학습된 표현의 풀림을 강제하는 것의 구체적인 이점을 조사하며,
- 여러 데이터셋을 다룰 수 있는 재현 가능한 실험 설정을 고려해보아야 한다
는 것을 말해준다.
실제 논문 서론에서 주장하는 contribution은,
- 풀린 표현의 무감독 학습은 ‘학습방법과 데이터셋 모두에 대한 귀납적 편향’ 없이는 본질적으로 불가능함을 이론적으로 보인 것
- 현재의 여러 무감독 풀림 학습 방법들을 조사 및 구현하여 이를 여러 데이터셋과 모델을 학습시킨 것
- 풀린 표현을 학습하고 평가하는 disentanglement_lib라는 새로운 라이브러리를 공개한 것
- 상당한 계산량을 필요로 하는 1만 개 이상의 사전 학습된(pre-trained) 모델을 공개한 것
- 무감독 풀림 학습에 대한 여러 생각들을 검증해보았다:
- 고려된 모든 방법들이 샘플링된 posterior들의 차원(dimensions)의 독립성을 보장한다고 해도, 표현의 차원을 상관관계가 있다.
- random seed와 hyperparameter이라는 무감독 조건 하에서 고려된 모델들이 풀린 표현을 더 잘 학습한다는 증거가 없다.
- (데이터셋을 통한 훌륭한(학습이 잘 되는) hyperparameter들을 주는 것을 허용한다 할지라도) ‘ground-truth 레이블에 접근할 수 없는’ 잘 학습된 모델은 식별될 수 없다.
- 고려된 모델과 데이터셋에 대해, 학습의 샘플 복잡도의 감소와 같은 downstream task에 풀림이 유용하지 않다.
- 실험 결과에 의해, 향후 연구에 대한 세 가지 중요한 부분을 제안하였다: 이는 초록 부분과 같다.
Rates of Convergence for Sparse Variational Gaussian Process Regression
| 개요 | 내용 |
|---|---|
| 저자 | David R. Burt, et al. University of Cambridge and PROWLER. io |
| 논문 링크 | https://arxiv.org/abs/1903.03571 |
| 제출일 | Submitted on 8 Mar 2019 (v1), last revised 3 Jul 2019 (this version, v2) |
초록
Gaussian process posteriors에 대한 훌륭한 변분 근사법(variational approximations)은 데이터셋 크기 $N$에 대해 $O(N^3)$의 시간이 걸리는 것을 막기 위해 개발되었다. 이 방법은 시간복잡도를 $O(N^3)$에서 $O(NM^2), M \ll N $의 시간으로 줄여 주었다.
$M$은 이 preocess를 요약하는 유도변수(inducing variables)인데, 수행시간은 $N$에 선형 비례함에도 불구하고 실제로는 근사의 품질을 결정하는 $M$이 얼마나 큰지에 실질적인 영향을 더 받는다.
이 논문에서, $N$에 비해 훨씬 느리게 증가하는 어떤 $M$에 대해 높은 확률로 KL divergence를 임의로 작게 만들 수 있음을 보인다. 특히 Square Exponential kernel을 쓰는 D차원의 정규분포 입력에 대한 회귀의 경우 $M = O(log^D N)$이면 충분하다.
이 논문의 결과는 데이터셋이 커질수록 Gaussian process posteriors는 적은 비용으로 근사될 수 있으며, 연속학습 시나리오(continual learning scenarios)에서 $M$을 증가시키는 구체적인 방법을 보이는 것이다.
서론
Gaussian processes(GPs)는 베이지안 모델에서 convenient priors인 함수에 대한 분포이다. 이는 좋은 불확실성 측정을 해내기 때문에 특히 회귀 모델에서 자주 사용되며, 사후확률(posterior)과 주변확률(marginal likelihood)에 대한 닫힌 표현(closed-form expressions)를 가진다. 이것의 가장 큰 단점은 학습 데이터 수 $N$에 대해 $O(N^3)$의 계산량과 $O(N^2)$의 메모리를 쓴다는 것이다. Low-rank approximations(Quiñonero Candela & Rasmussen, 2005)는 전체 사후확률을 요약하는 $M$개의 유도변수를 사용하여 계산량을 $O(NM^2 + M^3)$, 메모리 사용량을 $O(NM + M^2)$로 줄였다.
유도변수를 추가함으로써 계산량이 줄어드는 것은 알려져 있지만, 얼마나($M$) 필요한지에 대한 정보는 별로 없다. 데이터셋이 커질수록 우리는 품질저하 없이 근사상수의 수용력이 얼마나 될지 기대할 수 없다. 단지 $N$이 커질수록 $M$이 커져야 한다는 것만 알 뿔이다.
근사 GPs는 종종 근사사후확률에서 전체사후확률과정으로의 KL divergence를 최소화하는 변분추론(variational inference)을 써서 학습된다(Titsias, 2009, Matthews et al, 2016). 이 논문에서는 근사사후확률의 품질을 위한 측정방법으로 KL divergence를 사용한다.
직관적인 가정 하에 유도변수의 수는 선형보다 느리게 증가하는 정도면 된다(예: 로그함수). 이는 많은 편향(bias)의 필요 없이 정확도와 불확실성에 대한 정확도를 보유한 근사사후확률만으로 큰 데이터셋에 대해 아주 희박한 근사만 있어도 된다는 것을 보여준다.
이 논문에서 나오는 증명의 핵심 아이디어는 데이터의 공분산행렬에 대한 Nyström 근사의 품질에 의존하는 KL divergence의 상한(상계)를 사용하는 것이다. 이 error는 무한차원의 필수연산자라는 개념으로 이해될 수 있다. Stationery kernel에 대해 메인 결과는 사전확률(priors)는 샘플함수보다 더 매끈하며(smoother) 더 집중되어 있는(more concentrated) 데이터셋은 더 희박한(sparse) 근사만으로도 충분하다는 것이다.
메인 결과
학습 입력은 고정된 독립항등분포로부터 나온 것이라는 가정 하에, 적어도 $1-\delta$의 확률로
\[KL(Q \Vert \hat{P}) \le \mathcal{O} \Bigg( \frac{g(M, N)}{\sigma^2_n \delta}\Big(1 + \frac{c\Vert y \Vert^2_2}{\sigma^2_n}\Big) + N \epsilon \Bigg)\]$\hat{P}$은 posterior Gaussian process, $Q$는 변분근사, $y$는 학습 목표(training targets)이다.
함수 $g(M, N)$은 kernel과 입력의 분포에 의존하며, $N$에 따라 선형적으로 증가하며 $M$에 따라 빠르게 감소한다.
$\epsilon$은 초기품질을 결정짓는 인자로서 약간의 계산을 추가하여 임의로 작게 만들 수 있다($N$의 역승).
참고: Gaussian process regression
학습 데이터
\[\mathcal{D}= \{ x_i, y_i \}^N_{i=1}, x_i \in \chi, y_i \in \mathbb{R}\]가 관측되었을 때 Gaussian process regression을 고려해본다. 이 때 목표는 학습데이터의 제한된 수로 인해 $f(\cdot)$에 대한 불확실성을 갖고 있을 때 새로운 입력 $x^\ast$에 대해 출력값 $y^\ast$를 예측하는 것이다. $f$에 대한 사전확률을 두는 베이지안 접근법과 약간의 noise를 가진 곽츤 데이터에 대한 $f$의 우도를 고려할 때, 모델은
\[f \sim \mathcal{GP}(\nu(\cdot), k(\cdot, \cdot)), \ y_i = f(x_i) + \epsilon_i, \ \epsilon_i \sim \mathcal{N}(0, \sigma^2_n)\]$\nu : \chi \rightarrow \mathbb{R}$은 평균함수이고 $k : \chi \times \chi \rightarrow \mathbb{R}$은 공분산함수이다. 로그주변우도(log marginal likelihood)는 근사의 품질과 사후확률근사가 연관되어 있다는 점에서 흥미로우며, 이는
\[\mathcal{L} = -\frac{1}{2} y^T K_n^{-1} y - \frac{1}{2} log \vert K_n \vert - \frac{N}{2} log(2\pi), \quad K_n = K_{ff} + \sigma^2_n I, \ [K_{ff}]_{i, j} = k(x_i, x_j)\]으로 표현된다.
Training Neural Networks with Local Error Signals
| 개요 | 내용 |
|---|---|
| 저자 | Arild Nøkland, Lars Hiller Eidnes |
| 논문 링크 | https://arxiv.org/abs/1901.06656 |
| 소스코드 | https://github.com/anokland/local-loss |
| 제출일 | Submitted on 20 Jan 2019 (v1), last revised 7 May 2019 (this version, v2) |
최근 분류(classification)를 위한 신경망의 감독학습(supervised learning)은 보통 global loss function을 사용하여 이루어졌다. 즉, 모델을 학습시키는 데 있어서 하나의 loss function만을 설정해 두고, prediction 단계에서 계산한 loss로 backward pass 동안 gradient를 계산하며 weights를 업데이트하는 역전파(back-propagation) 과정을 거쳐왔다.
그러나 이 논문에서는 하나의 loss function을 모델의 모든 레이어에 걸쳐 global하게 사용하는 대신 각 레이어별로 loss function을 설정하여 실험하였고, 이 방법은 생물학적으로 그럴듯하고(biologically plausible) 그러면서도 여전히 state-of-the-art 결과를 얻을 수 있음을 보여주었다.
Global loss function의 사용은 다음과 같은 문제를 갖는다.
- Backward locking problem: hidden layer의 weights들은 forward & backward pass가 끝날 때까지 업데이트되지 않는다. 따라서 weights update의 병렬화가 어렵다.
- Preventing reuse of the memory: hidden layer의 activation들을 backward pass가 끝날 때까지 메모리에 상주시켜야 하기 때문에 메모리 사용량이 늘어난다.
- Biologically implausible: global loss의 역전파는 신경망이라는 관점에서 생물학적으로 별로 타당하지 않다.
이 논문에서, backward locking problem은 지역적으로(각 레이어별로) 측정된 error에 의해 각각 학습시킴으로써 해결될 수 있음을 보인다. Local loss function은 global error에 의존하지 않고, gradient는 해당 레이어를 제외한 그 이전 레이어에 전파되지 않으며, hidden layer는 forward pass 중간에도 업데이트될 수 있다.
추론(inference) 단계에서 네트워크는 global 역전파를 쓰는 것과 같이 움직인다. 그러나 hidden layer가 업데이트될 때, gradient와 activation은 더 이상 메모리에 남아 있을 필요가 없다.
따라서 모든 레이어를 동시에 학습시킴에도, 지역적으로 측정된 error는 각 레이어를 학습시키며 이것을 메모리 사용량과 학습 시간을 줄여줄 수 있게 된다.
관련 연구는 Local Loss Functions, Similarity Measures in Neuroscience/Machine Learning 등이 있다(논문 참조).
표준 convolutional & fully connected 네트워크 구조를 사용하여, global loss 대신 각 레이어별로 (이전 레이어로 전파되지 않는) local learning signal을 설정했다. 이 signal은 2개의 single-layer sub-networks로 분리되어, 각각은 서로 다른 loss function을 갖는다. 하나는 표준 cross-entropy loss이고, 다른 하나는 similarity matching loss이다.
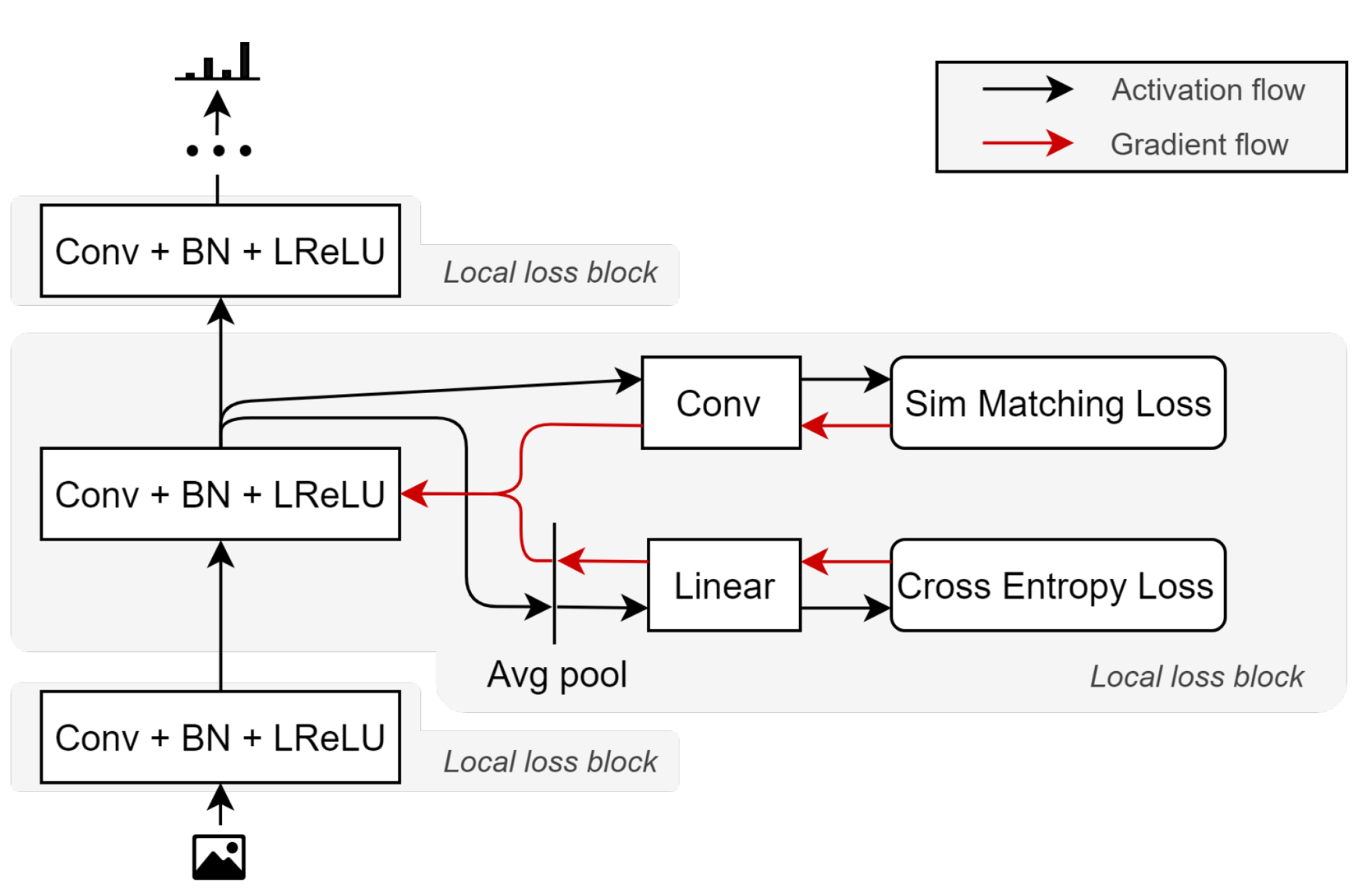
논문에서는 여러 loss를 정의하는데,
- sim loss: mini-batch의 example들 간 pair-wise 유사도를 담고 있는 두 행렬간 L2 거리를 측정하는 similarity matching loss이다.
- pred loss: target과 local classifier의 prediction 간 cosss-entropy loss를 측정한다.
- sim-bpf loss & pred-bpf loss: Backprop free version을 만들기 위해, global target이 각 hidden layer로 전파되는 것을 막는다. sim loss에서는 one-hot encoded target vector 대신 random transformation target vector를, pred loss에서는 binarized random transformation target vector를 사용한다.
- predsim & predsim-bpf loss: sim과 pred를 조합해서 전체 loss를 만들었다.
실험은 MNIST, Fashion-MNIST, Kuzushiji-MNIST, CIFAR-10, CIFAR-100, STL_10, SVHN에 대해서 각각 진행하였다.
결과를 요약하자면 단지 local pred loss만으로도 global 역전파를 사용한 것과 거의 같은 성능을 보였고, predsim이나 predsim-bpf를 사용한 경우 state-of-the-art 결과를 얻을 수 있었다고 한다.
따라서 이 논문의 contribution은 loss function을 굳이 global하게 만들지 말고 각 레이어별로 local loss function을 만들어서 backward locking problem과 parallelization을 해결하는 것이 학습속도, 생물학적 타당성, 분류 성능을 다 잡을 수 있다는 가능성을 보여준 것이 되겠다.

