Imbalanced Learning
01 Oct 2019 | Machine_Learning Paper_Review Imbalanced Learning목차
1. Imbalanced Learning (불균형 학습) 개요
비정상 거래 탐지와 같은 케이스의 경우, 정상적인 거래 보다는 정상 범위에서 벗어난 것으로 판단되는 거래 기록의 비중이 현저하게 작을 것이다. 그런데 보통의 알고리즘으로 이러한 비정상 거래를 찾아내기 에는 이러한 데이터의 불균형이 중요한 이슈로 작용하는데, 본 글에서는 이러한 불균형 학습과 관련된 논의를 해보고자 한다.
알고리즘 자체로 Class 불균형을 해소하는 방법을 제외하면, Over-Sampling과 Under-Sampling 방법이 가장 대표적인 방법이라고 할 수 있다.
1.1. Over-Sampling
Over-Sampling은 부족한 데이터를 추가하는 방식으로 진행되며, 크게 3가지로 구분할 수 있다.
첫 번째 방법은 무작위 추출인데, 단순하게 랜덤하게 부족한 Class의 데이터를 복제하여 데이터셋에 추가하는 것이다.
두 번째 방법은 위와 달리 기존 데이터를 단순히 복사하는 것에 그치지 않고, 어떠한 방법론에 의해 합성된 데이터를 생성하는 것이다. 이후에 설명할 SMOTE 기법이 본 방법의 대표적인 예에 해당한다.
세 번째 방법은 어떤 특별한 기준에 의해 복제할 데이터를 정하고 이를 실행하는 것이다.
1.2. Under-Sampling
Over-Sampling과 반대로 Under-Sampling은 정상 데이터의 수를 줄여 데이터셋의 균형을 맞추는 것인데, 주의해서 사용하지 않으면 매우 중요한 정보를 잃을 수도 있기 때문에 확실한 근거를 바탕으로 사용해야 하는 방법이다.
Under-Sampling의 대표적인 예로는 RUS가 있고, 이는 단순히 Random Under Sampling을 뜻한다.
2. SMOTE 기법
SMOTE는 Synthetic Minority Oversampling TEchnique의 약자로, 2002년에 처음 등장하여 현재(2019.10)까지 8천 회가 넘는 인용 수를 보여주고 있는 Over-Sampling의 대표적인 알고리즘이다.
알고리즘의 원리 자체는 간단하다. Boostrap이나 KNN 모델 기법을 기반으로 하는데, 그 원리는 다음과 같다.
- 소수(위 예시에선 비정상) 데이터 중 1개의 Sample을 선택한다. 이 Sample을 기준 Sample이라 명명한다.
- 기준 Sample과 거리(유클리드 거리)가 가까운 k개의 Sample(KNN)을 찾는다. 이 k개의 Sample 중 랜덤하게 1개의 Sample을 선택한다. 이 Sample을 KNN Sample이라 명명한다.
-
새로운 Synthetic Sample은 아래와 같이 계산한다. \(X_{new} = X_i + (X_k - X_i) * \delta\)
$X_{new}$: Synthetic Sample
$X_i$: 기준 Sample
$X_k$: KNN Sample
$\delta$: 0 ~ 1 사이에서 생성된 난수
본 과정을 일정 수 만큼 진행하면 아래 그림과 같이 새로운 합성 데이터가 생성됨을 알 수 있다.

간단한 예시를 보면,
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
from sklearn.datasets import make_classification
from imblearn.over_sampling import SMOTE
from sklearn.preprocessing import MinMaxScaler
x, y = make_classification(n_features=2, n_informative=2, n_samples=20, weights= [0.8, 0.2],
n_redundant=0, n_clusters_per_class=1, random_state=0)
scaler = MinMaxScaler(feature_range=(0, 1))
x = scaler.fit_transform(x)
# SMOTE 이전
df1 = pd.DataFrame(np.concatenate([x, y.reshape(-1, 1)], axis=1),
columns=['col1', 'col2', 'result'])
sns.relplot(x='col1', y='col2', hue='result', data=df1)
plt.show()
# SMOTE 이후
sm = SMOTE(ratio='auto', kind='regular', k_neighbors=3)
X, Y = sm.fit_sample(x, list(y))
df2 = pd.DataFrame(np.concatenate([X, Y.reshape(-1, 1)], axis=1),
columns=['col1', 'col2', 'result'])
sns.relplot(x='col1', y='col2', hue='result', data=df2)
plt.show()
다음 그림들에서 위는 SMOTE 이전의 데이터를, 아래는 SMOTE 이후의 데이터 분포를 보여준다.
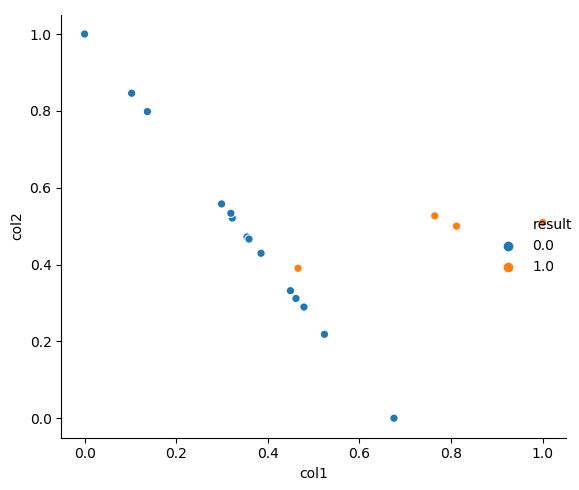
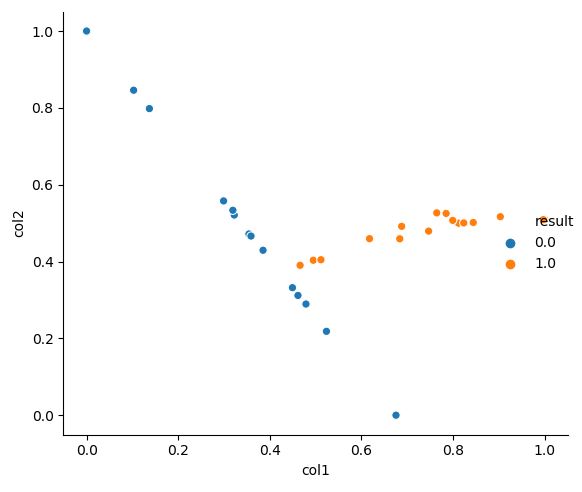
3. 추가할 것
MSMOTE, Borderline SMOTE, Adasyn
Reference
참고 블로그
파이썬 머신러닝 완벽 가이드, 권철민, 위키북스

