Light GBM 설명 및 사용법
09 Dec 2019 | Machine_Learning목차
1. Light GBM: A Highly Efficient Gradient Boosting Decision Tree 논문 리뷰
1.1. Background and Introduction
다중 분류, 클릭 예측, 순위 학습 등에 주로 사용되는 Gradient Boosting Decision Tree (GBDT)는 굉장히 유용한 머신러닝 알고리즘이며, XGBoost나 pGBRT 등 효율적인 기법의 설계를 가능하게 하였다. 이러한 구현은 많은 엔지니어링 최적화를 이룩하였지만 고차원이고 큰 데이터 셋에서는 만족스러운 결과를 내지 못하는 경우도 있었다. 왜냐하면 모든 가능한 분할점에 대해 정보 획득을 평가하기 위해 데이터 개체 전부를 스캔해야 했기 때문이다. 이는 당연하게도, 굉장히 시간 소모적이다.
본 논문은 이 문제를 해결하기 위해 2가지 최신 기술을 도입하였다.
첫 번째는 GOSS: Gradient-based One-Side Sampling이며, 기울기가 큰 데이터 개체가 정보 획득에 있어 더욱 큰 역할을 한다는 아이디어에 입각해 만들어진 테크닉이다. 큰 기울기를 갖는 개체들은 유지되며, 작은 기울기를 갖는 데이터 개체들은 일정 확률에 의해 랜덤하게 제거된다.
두 번째는 EFB: Exclusive Feature Bundling으로, 변수 개수를 줄이기 위해 상호배타적인 변수들을 묶는 기법이다. 원핫 인코딩된 변수와 같이 희소한(Sparse) 변수 공간에서는 많은 변수들이 상호 배타적인 경우가 많다. (0이 굉장히 많기 때문에) 본 테크닉은, 최적 묶음 문제를 그래프 색칠 문제로 치환하고 일정 근사 비율을 갖는 Greedy 알고리즘으로 이 문제를 해결한다.
1.2. Preliminaries
GBDT는 Decision Tree의 앙상블 모델이다. 각각의 반복에서 GBDT는 음의 기울기(잔차 오차)를 적합함으로써 Decision Tree를 학습시킨다. 이 학습 과정에서 가장 시간이 많이 소모되는 과정이 바로 최적의 분할점들을 찾는 것인데, 이를 위한 대표적인 방법에는 Pre-sorted(사전 정렬) 알고리즘과 Histogram-based 알고리즘이 있다.
Pre-sorted 알고리즘의 경우 사전 정렬한 변수 값에 대해 가능한 모든 분할점을 나열함으로써 간단하게 최적의 분할점을 찾을 수 있지만, 효율적이지 못하다는 단점이 있다. Histogram-based 알고리즘은 연속적인 변수 값을 이산적인 구간(bin)으로 나누고, 이 구간을 사용하여 학습과정 속에서 피쳐 히스토그램을 구성한다.
학습 데이터의 양을 줄이기 위해 가장 쉽게 생각할 수 있는 방법은 Down Sampling이 될 것이다. 이는 만약 데이터 개체의 중요도(Weight)가 설정한 임계값을 넘지 못할 경우 데이터 개체들이 필터링되는 과정을 말한다. SGB의 경우 약한 학습기를 학습시킬 때 무작위 부분집합을 사용하지만, SGB를 제외한 Down Sampling 방식은 AdaBoost에 기반하였기 때문에 바로 GBDT에 적용시킬 수 없다. 왜냐하면 AdaBoost와 달리 GBDT에는 데이터 개체에 기본 가중치가 존재하지 않기 대문이다.
비슷한 방식으로 피쳐 수를 줄이기 위해서는, 약한(Weak) 피쳐를 필터링하는 것이 자연스러울 것이다. 그러나 이러한 접근법은 변수들 사이에 중대한 중복요소가 있을 것이라는 가정에 의존하는데, 실제로는 이 가정이 옳지 않을 수도 있다.
실제 상황에서 사용되는 대용량 데이터셋은 많은 경우에 희소한(Sparse) 데이터셋일 확률이 높다. Pre-sorted 알고리즘에 기반한 GBDT의 경우 0값을 무시함으로써 학습 비용을 절감할 수 있지만, Histogram-based 알고리즘에 기반한 GBDT에는 효율적인 희소값 최적화 방법이 없다. 그 이유는 Histogram-based 알고리즘은 피쳐 값이 0이든 1이든, 각 데이터 개체마다 피쳐 구간(Bin) 값을 추출해야하기 때문이다. 따라서 Histogram-based 알고리즘에 기반한 GBDT가 희소 변수를 효과적으로 활용할 방안이 요구된다. 이를 해결하기 위한 방법이 바로 앞서 소개한 GOSS와 EFB인 것이다. GOSS는 데이터 개체 수를 줄이고, EFB는 피쳐 수를 줄이는 방법론이다.
1.3. GOSS: Gradient-based One-Sided Sampling
AdaBoost에서 Sample Weight는 데이터 개체의 중요도를 알려주는 역할을 수행하였다. GBDT에서는 기울기(Gradient)가 이 역할을 수행한다. 각 데이터 개체의 기울기가 작으면 훈련 오차가 작다는 것을 의미하므로, 이는 학습이 잘 되었다는 뜻이다. 이후 이 데이터를 그냥 제거한다면 데이터의 분포가 변화할 것이므로, 다른 접근법(GOSS)이 필요하다.
GOSS의 아이디어는 직관적이다. 큰 Gradient(훈련이 잘 안된)를 갖는 데이터 개체들은 모두 남겨두고, 작은 Gradient를 갖는 데이터 개체들에서는 무작위 샘플링을 진행하는 것이다. 이를 좀 더 상세히 설명하자면 아래와 같다.
1) 데이터 개체들의 Gradient의 절대값에 따라 데이터 개체들을 정렬함
2) 상위 100a% 개의 개체를 추출함
3) 나머지 개체들 집합에서 100b% 개의 개체를 무작위로 추출함
4) 정보 획득을 계산할 때, 위의 2-3 과정을 통해 추출된 Sampled Data를 상수( $ \frac{1-a} {b} $ )를 이용하여 증폭시킴

위 그림에 대하여 추가적으로 부연설명을 하면,
topN, randN은 2, 3 과정에서 뽑는 개수를 의미하며,
topSet, randSet 은 2, 3 과정에서 뽑힌 데이터 개체 집합을 의미한다.
w[randSet] x= fact은 증폭 벡터를 구성하는 과정으로, 증폭 벡터는 randSet에 해당하는 원소는 fact 값을 가지고, 나머지 원소는 1의 값을 가지는 벡터이다.
마지막으로 L: Weak Learner에 저장된 정보는, 훈련데이터, Loss, 증폭된 w벡터로 정리할 수 있겠다.
1.4. EFB: Exclusive Feature Bundling
희소한 변수 공간의 특성에 따라 배타적인 변수들을 하나의 변수로 묶을 수 있다. 그리고 이를 배타적 변수 묶음(Exclusive Feature Bundle)이라고 부른다. 정교하게 디자인된 변수 탐색 알고리즘을 통해, 각각의 변수들로 했던 것과 마찬가지로 변수 묶음들로부터도 동일한 변수 히스토그램들을 생성할 수 있게 된다.
이제 1) 어떤 변수들이 함께 묶여야 하는지 정해야 하며, 2) 어떻게 묶음을 구성할 것인가에 대해 알아볼 것이다.
정리: 변수들을 가장 적은 수의 배타적 묶음으로 나누는 문제는 NP-hard이다.
(NP-hard의 뜻을 알아보기 위해서는 이곳을 참조하길 바란다.)
증명: 그래프 색칠 문제를 본 논문의 문제로 환원한다. 그래프 색칠 문제는 NP-hard이므로 우리는 결론은 추론 가능하다.
$ G = (V, E) $ 라는 임의의 그래프가 있다고 하자. 이 G의 발생 행렬(Incidence Matrix)의 행들이 우리 문제의 변수에 해당한다. 위 정리에서 최적의 묶음 전략을 찾는 것은 NP-hard라고 하였는데, 이는 다항 시간 안에 정확한 해를 구하는 것이 불가능하다는 의미이다. 따라서 좋은 근사 알고리즘을 찾기 위해서는 최적 묶음 문제를 그래프 색칠 문제로 치환해야 한다. 이 치환은 변수(feature)들을 꼭짓점(vertices)으로 간주하고 만약 두 변수가 상호배타적일 경우 그들 사이에 변(edge)을 추가하는 방식으로 이루어진다. 이후 Greedy 알고리즘을 사용한다.
1)에 관한 알고리즘을 설명하자면 다음과 같다.
- 각 변마다 가중치가 있는 그래프를 구성하는데, 여기서 가중치는 변수들간의 충돌(conflicts)을 의미한다. 여기서 충돌이란 non-zero value가 동시에 존재하여 상호배타적이지 않은 상황을 의미한다.
- 그래프 내에 있는 꼭짓점 차수에 따라 내림차순으로 변수들을 정렬한다.
- 정렬한 리스트에 있는 각 변수를 확인하면서 이들을 작은 충돌(γ로 제어함)이 있는 기존 묶음에 할당하거나, 새로운 묶음을 만든다.

이 알고리즘의 시간 복잡도는 변수들의 개수의 제곱에 해당하며, 이는 나름 괜찮은 수준이지만 만약 변수들의 수가 매우 많다면 개선이 필요하다고 판단된다. 따라서 본 논문은 그래프를 직접 구성하지 않고 0이 아닌 값의 개수에 따라 정렬하는 방식(0이 아닌 값이 많을 수록 충돌을 일으킬 확률이 높으므로)으로 알고리즘을 수정하였다.
2)에 관해서 이야기하자면, 가장 중요한 것은 변수 묶음들로부터 원래(original) 변수들의 값을 식별할 수 있어야 한다는 것이다. Histogram-based 알고리즘은 변수의 연속적인 값 대신 이산적인 구간(bin)을 저장하므로, 배타적 변수들을 각각 다른 구간에 두어 변수 묶음을 구성할 수 있다. 이는 변수의 원래 값에 offset을 더하는 것으로 이루어 질 수 있다.
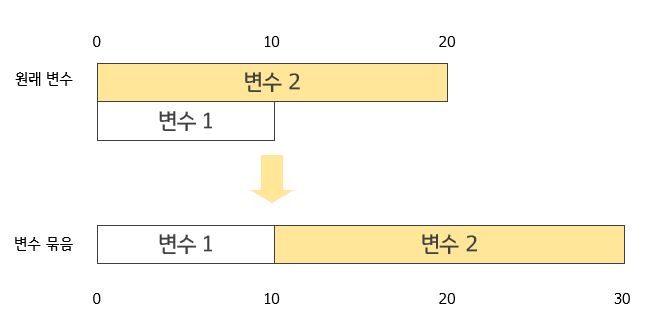
예를 들어 변수 묶음에 변수 2개가 속한다고 할 때,
원래 변수 A는 [0, 10)의 값을 취하고, 원래 변수 B는 [0, 20)의 값을 취한다.
이대로 두면 [0, 10) 범위 내에서 두 변수는 겹칠 것이므로,
변수 B에 offset 10을 더하여 가공한 변수가 [10, 30)의 값을 취하게 한다.
이후 A, B를 병합하고 [0, 30] 범위의 변수 묶음을 사용하여 기존의 변수 A, B를 대체한다.

2. Light GBM 적용
본 글에서는 Kaggle-Santander 데이터를 이용하여 간단한 적용 예시를 보이도록 하겠다. 초기에 lightgbm은 독자적인 모듈로 설계되었으나 편의를 위해 scikit-learn wrapper로 호환이 가능하게 추가로 설계되었다. 본 글에서는 scikit-learn wrapper Light GBM을 기준으로 설명할 것이다.
# Santander Data
ID var3 var15 ... saldo_medio_var44_ult3 var38 TARGET
0 1 2 23 ... 0.0 39205.17 0
1 3 2 34 ... 0.0 49278.03 0
2 4 2 23 ... 0.0 67333.77 0
[3 rows x 371 columns]
n_estimators 파라미터는 반복 수행하는 트리의 개수를 의미한다. 너무 크게 지정하면 학습 시간이 오래 걸리고 과적합이 발생할 수 있으니, 파라미터 튜닝 시에는 크지 않은 숫자로 지정하는 것이 좋다. num_leaves 파라미터는 하나의 트리가 가질 수 있는 최대 리프의 개수인데, 이 개수를 높이면 정확도는 높아지지만 트리의 깊이가 커져 모델의 복잡도가 증가한다는 점에 유의해야 한다.
먼저 기본적인 모델을 불러온다.
from lightgbm import LGBMClassifier
lgbm = LGBMClassifier(n_estimators=200)
공식문서을 참조하면 아래와 같은 몇몇 주의사항을 볼 수 있다.
Light GBM은 leaf-wise 방식을 취하고 있기 때문에 수렴이 굉장히 빠르지만, 파라미터 조정에 실패할 경우 과적합을 초래할 수 있다.
max_depth 파라미터는 트리의 최대 깊이를 의미하는데, 위에서 설명한 num_leaves 파라미터와 중요한 관계를 지닌다. 과적합을 방지하기 위해 num_leaves는 2^(max_depth)보다 작아야 한다. 예를 들어 max_depth가 7이기 때문에, 2^(max_depth)=98이 되는데, 이 때 num_leaves를 이보다 작은 70~80 정도로 설정하는 것이 낫다.
min_child_samples 파라미터는 최종 결정 클래스인 Leaf Node가 되기 위해서 최소한으로 필요한 데이터 개체의 수를 의미하며, 과적합을 제어하는 파라미터이다. 이 파라미터의 최적값은 훈련 데이터의 개수와 num_leaves에 의해 결정된다. 너무 큰 숫자로 설정하면 under-fitting이 일어날 수 있으며, 아주 큰 데이터셋이라면 적어도 수백~수천 정도로 가정하는 것이 편리하다.
sub_sample 파라미터는 과적합을 제어하기 위해 데이터를 샘플링하는 비율을 의미한다.
지금까지 설명한 num_leaves, max_depth, min_child_samples, sub_sample 파라미터가 Light GBM 파라미터 튜닝에 있어서 가장 중요한 파라미터들이다. 이들은 하나씩 튜닝할 수도 있고, 한 번에 튜닝할 수도 있다. 학습 데이터의 성격과 여유 시간에 따라 선택해야 한다. 이들에 대한 최적값을 어느 정도 확보했다면, 다음 단계로 넘어가도 좋다.
colsample_bytree 파라미터는 개별 트리를 학습할 때마다 무작위로 선택하는 피쳐의 비율을 제어한다. reg_alpha는 L1 규제를, reg_lambda는 L2 규제를 의미한다. 이들은 과적합을 제어하기에 좋은 옵션들이다.
learning_rate은 후반부에 건드리는 것이 좋은데, 초반부터 너무 작은 학습률을 지정하면 효율이 크게 떨어질 수 있기 때문이다. 정교한 결과를 위해, 마지막 순간에 더욱 좋은 결과를 도출하기 위해 영혼까지 끌어모으고 싶다면, learning_rate는 낮추고 num_estimators는 크게 하여 최상의 결과를 내보도록 하자.
다음은 위에서 처음 소개한 Santander Data를 바탕으로 한 예시이다.
params = {'max_depth': [10, 15, 20],
'min_child_samples': [20, 40, 60],
'subsample': [0.8, 1]}
grid = GridSearchCV(lgbm, param_grid=params)
grid.fit(X_train, Y_train, early_stopping_rounds=100, eval_metric='auc',
eval_set=[(X_train, Y_train), (X_val, Y_val)])
print("최적 파라미터: ", grid.best_params_)
lgbm_roc_score = roc_auc_score(Y_test, grid.predict_proba(X_test)[:, 1], average='macro')
print("ROC AUC: {0:.4f}".format(lgbm_roc_score))
# 위 결과를 적용하여 재학습
lgbm = LGBMClassifier(n_estimators=1000, num_leaves=50, subsample=0.8,
min_child_samples=60, max_depth=20)
evals = [(X_test, Y_test)]
lgbm.fit(X_train, Y_train, early_stopping_rounds=100, eval_metric='auc',
eval_set=evals, verbose=True)
score = roc_auc_score(Y_test, grid.predict_proba(X_test)[:, 1], average='macro')
print("ROC AUC: {0:.4f}".format(score))
Reference
LightGBM 공식 문서
논문 파이썬 머신러닝 완벽 가이드, 권철민, 위키북스

