잠재요인 협업필터링 (Latent Factor Collaborative Filtering) 설명
17 Dec 2019 | Machine_Learning Recommendation System Matrix Factorization Latent Factor Collaborative Filtering목차
- 1. Introduction
- 2. 추천 시스템의 개요
- 3. Singular Value Decomposition
- 4. 잠재 요인 협업 필터링의 Matrix Factorization
- 5. 간단한 예제
- 6. Surprise 모듈을 활용한 예제
- Reference
1. Introduction
추천시스템은 이제는 너무 많은 산업에서 도입하고 있는 시스템이기에 웬만큼 참신하지 않은 이상 새롭게 들리지 않는 것이 현실이다. 그러나 소비자의 입장에서 추천시스템을 보는 것과, 이 시스템의 개발자가 추천시스템을 바라 보는 것에는 큰 차이가 있다. 성공적으로 추천 엔진을 도입한 산업, 기업들이 있는 반면 여러 가지 어려움으로 인해 실질적인 효과가 떨어지는 산업, 기업도 있기 마련이다.
사용자(User)의 행동 양식, 인구학적(Demographic) 정보, 아이템(Item)의 특성, 외부 변수 등 수많은 변인들을 관리하고 분석해서 사용자에게 가장 알맞는 아이템을 추천해주는 일은 분명 쉬운 일은 아니다. 이러한 어려움을 극복하기 위해 연구자들은 과거부터 여러 종류의 추천 시스템을 개발해왔는데, 지금부터 그에 대해 조금씩 알아보고자 한다.
추천 시스템을 만드는 방법에는 굉장히 다양한 방식이 존재하지만, 본 글에서는 가장 핵심이 되는 방법론들에 대해서만 간단히 언급하고자 한다. 추천 시스템은 크게 컨텐츠 기반 필터링(Content Based Filtering) 방식과 협업 필터링(Collaborative Filterin) 방식으로 나뉜다. 협업 필터링은 또 최근접 이웃(Nearest Neighbor) 협업 필터링과 잠재 요인(Latent Factor) 협업 필터링으로 나뉜다.
과거에는 컨텐츠 기반 필터링과 최근접 이웃 협업 필터링이 더욱 주목을 받았지만, 2009년에 있었던 넷플릭스 추천 컴퍼티션에서 행렬 분해(Matrix Factorization)를 이용한 잠재 요인 협업 필터링 방식이 우승을 차지하면서, 연구자들은 이 방식에 큰 관심을 갖게 되었다. 현재로서는 많은 경우에 이 방식이 우위를 차지하지만, 상황에 따라서는 다른 방식이 더 좋은 결과를 낼 때도 많고, 하이브리드 형식으로 결합하는 방식 또한 좋은 효율을 보여주는 경우도 많다.
아래에서 보충 설명을 하겠지만 추천 시스템의 대표적인 방법론들을 구조화하면 아래와 같다.
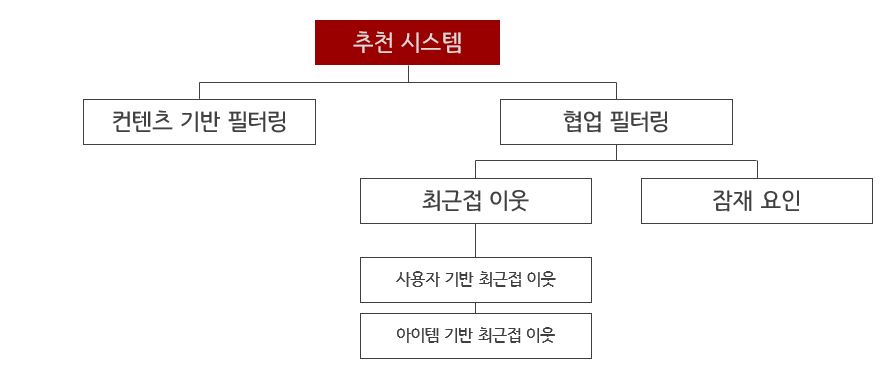
앞으로 여러 시리즈로 이어질 추천 시스템에 관한 글들은, 위에서 언급한 잠재 요인 협업 필터링과 이 방법론에서 출발하여 발전된 알고리즘에 대해 다룰 예정이다.
Matrix Factorization 개념에 Support Vector Machine의 개념을 결합한 것이 Factorization Machines이다. 여기서 더 나아가 개별 feature들의 메타정보(field)를 알고리즘에 반영한 것이 Field-aware Factorization Machines이다. 줄여서 각각 FM과 FFM이라고 부르는 것이 일반적이다.
로지스틱 모델과 달리 FFM은 가중치를 latent vector화 했기 때문에 연산량과 메모리 사용량이 더 많은 단점이 있지만, 최근 여러 논문에서는 system tuning을 통해 실제 광고 서빙에 사용하는 데 큰 지장이 없음을 밝혔다. 여력이 될 때 더욱 최신 연구들에 대해서도 글을 추가하도록 할 것이다.
2. 추천 시스템의 개요
2.1. 컨텐츠 기반 필터링
어떤 사용자가 특정 아이템을 선호할 때, 그 아이템과 비슷한 컨텐츠를 가진 다른 아이템을 추천하는 것이 이 방식의 기본 아이디어이다. 추가적으로 설명하자면, 이 방식은 사용자와 아이템에 대한 프로필을 만들고 그 특징을 활용한다. 예를 들어 어떤 특정 영화는 장르, 출연배우, 박스오피스 인기도 등 여러 특성을 지니게 될 텐데 이 특성(컨텐츠)들이 이 영화의 프로필을 형성하는 것이다.
2.2. 최근접 이웃 협업 필터링
모든 협업 필터링은 사용자-아이템 행렬 데이터에 의존한다. 사용자가 남긴 평점(rating) 데이터를 기반하여 남기지 않은 데이터를 추론하는 형식이다.
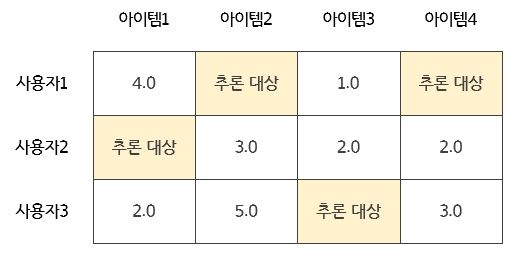
2.2.1. 사용자 기반 최근접 이웃 협업 필터링
특정 사용자와 유사한 사용자들을 선정하고, 이들을 TOP-N이라고 명명한 뒤 이들이 선호하는 아이템을 특정 사용자에게 추천하는 방식이다.
2.2.2. 아이템 기반 최근접 이웃 협업 필터링
어떤 사용자가 A라는 아이템을 선호한다고 할 때, 그 사용자는 A와 유사한 B라는 아이템 역시 선호할 것이라는 가정 하에 추천을 진행하는 방식이다. 아이템 기반 방식이 사용자 기반 방식 보다 정확도가 높은 것이 일반적이기에 본 방식이 더욱 자주 사용된다.
2.3. 잠재 요인 협업 필터링
사용자-아이템 평점 행렬에 잠재되어 있는 어떤 요인(factor)이 있다고 가정하고, 행렬 분해를 통해 그 요인들을 찾아내는 방식이다. 이 잠재 요인은 구체적으로 정의하는 것이 때로는 어렵지만, 실제 시스템에서는 추천의 근거를 마련하는 데에 있어 큰 역할을 수행한다.
예를 들어보면, 영화 장르를 잠재 요인으로 설정할 수 있다. 어떤 사용자는 판타지 영화를 다른 어떤 영화보다 좋아한다고 하면, 이 사용자에게 있어 영화를 선택할 때 가장 중요한 기준(요인)은 판타지 영화이냐 아니냐가 될 가능성이 높다. 그리고 이 사용자에게 다른 영화를 추천해준다고 한다면, 판타지 영화를 추천하는 것이 가장 합리적일 가능성이 높다는 것이다. 잠재 요인 협업 필터링은 이러한 요인들을 찾아 추천에 활용하게 된다.
지금부터는 이 행렬 분해를 어떻게 진행하는지에 대해 알아보도록 하겠다.
3. Singular Value Decomposition
특이값 분해는 Spectral Decomposition의 일반화 버전이라고 생각하면 쉽다. 즉, 정방행렬이라는 조건을 만족하지 않아도(행과 열의 개수가 달라도) 다차원 행렬을 저차원 행렬로 분해하는 차원 축소 기법이다.
Spectral Decomposition에 따르면 정방행렬 A는 아래와 같이 표현할 수 있다.
\[A = P\Lambda P' = P\Lambda P^T = \sum_{i=1}^{p} \lambda_i e_i e_i'\]여기서 $P$는 $\lambda$에 대응하는 고유벡터들을 열벡터로 가지는 직교행렬이다. $\Lambda$는 $A$의 고유값들을 대각원소로 가지는 대각행렬이다.
(m, n), m>n인 직사각 행렬 $A$에 대해 특이값 분해를 실시하면 아래와 같이 표현될 수 있다.
- $U$: (m, m), $A$의 left singular 벡터로 구성된 직교행렬
- $V$: (n, n), $A$의 right singular 벡터로 구성된 직교행렬
- $\Sigma$: (m, n), 주 대각성분이 $\sqrt{\lambda_i}$인 직사각 대각행렬
$AA^T$를 위 식으로 표현하면 아래와 같다.
\[AA^T = U\Sigma V^T V\Sigma U^T = U(\Sigma \Sigma^T) U^T\]여기서 $\Sigma \Sigma^T$는 $\Lambda$이다. (직접 계산해보라) 이 때문에 결과적으로 식은 아래와 같이 정리된다.
\[AA^T = U\Lambda U^T\]여기서 $U$는 정방행렬이기에 위에서 본 Spectral Decomposition의 식을 참조하면, $U$는 $AA^T$를 Eigenvalue Decomposition으로 직교대각화하여 얻은 직교행렬임을 알 수 있다. $A$의 rank가 k일 때, 이 $U$의 왼쪽에서부터 k번째 열벡터까지를 좌특이벡터(Left Singular Vectors)라고 부른다.
같은 방식으로 $A^TA = V\Lambda V^T$에서 $V$는 $A^TA$를 Eigenvalue Decomposition으로 직교대각화하여 얻은 직교행렬이 된다.
SVD를 기하학적으로 설명하면, $V^T, U$에 의해서 A 행렬의 방향이 변화하게 되고 $\Sigma$에 의해서 scale이 조정된다고 볼 수 있다.
4. 잠재 요인 협업 필터링의 Matrix Factorization
위에서 설명한 SVD는 잠재요인을 밝혀내기에 아주 적합한 방법이지만, 실제 현실에서 원행렬 A에는 결측값이(당연히 모든 사용자가 모든 아이템에 대해 평점을 남겼다면, 굳이 추천 시스템이 필요하지 않을 것이다.) 많다. 따라서 이를 대체할 근사적인 방법이 필요하며, 그 방법에는 SGD(Stochastic Gradient Descent) 또는 ALS(Alternating Least Squares)가 있다. 이 방법들에 대해서는 다음 글을 참조하기 바란다.
SGD를 이용해서 행렬을 분해하면 다음과 같다.
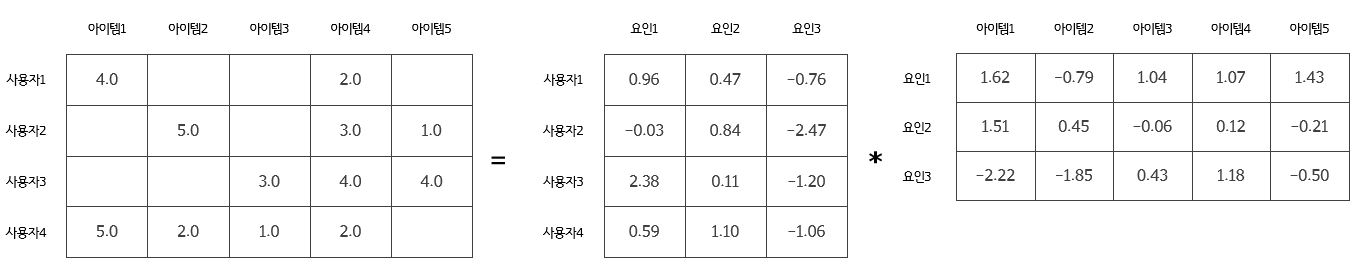
이 때 요인의 개수는 하이퍼파라미터로 임의로 조정하거나, Cross-Validation을 통해 최적의 값을 찾을 수 있다. 위에서 분해된 행렬을 다시 내적하여 원 행렬을 예측해보면 아래와 같이 크게 차이가 나지 않음을 알 수 있다.
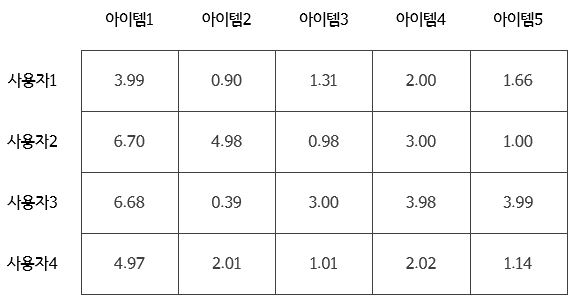
5. 간단한 예제
위에서 봤던 행렬 분해를 코드로 구현해보자. 좀 더 자세한 설명을 원한다면 아래 Reference에 있는 “파이썬 머신러닝 완벽 가이드”를 찾아보길 바란다.
import numpy as np
from sklearn.metrics import mean_squared_error
R = np.array([[4, np.NaN, np.NaN, 2, np.NaN],
[np.NaN, 5, np.NaN, 3, 1],
[np.NaN, np.NaN, 3, 4, 4],
[5, 2, 1, 2, np.NaN]])
# 실제 R 행렬과 예측 행렬의 오차를 구하는 함수
def calculate_rmse(R, P, Q, non_zeros):
error = 0
full_pred_matrix = np.dot(P, Q.T)
# 여기서 non_zeros는 아래 함수에서 확인할 수 있다.
x_non_zero_ind = [non_zeros[0] for non_zeros in non_zeros]
y_non_zero_ind = [non_zeros[1] for non_zeros in non_zeros]
# 원 행렬 R에서 0이 아닌 값들만 추출한다.
R_non_zeros = R[x_non_zero_ind, y_non_zero_ind]
# 예측 행렬에서 원 행렬 R에서 0이 아닌 위치의 값들만 추출하여 저장한다.
full_pred_matrix_non_zeros = full_pred_matrix[x_non_zero_ind, y_non_zero_ind]
mse = mean_squared_error(R_non_zeros, full_pred_matrix_non_zeros)
rmse = np.sqrt(mse)
return rmse
def matrix_factorization(R, K, steps=200, learning_rate=0.01, r_lambda=0.01):
num_users, num_items = R.shape
np.random.seed(1)
P = np.random.normal(scale=1.0/K, size=(num_users, K))
Q = np.random.normal(scale=1.0/K, size=(num_items, K))
# R>0인 행 위치, 열 위치, 값을 non_zeros 리스트에 저장한다.
non_zeros = [ (i, j, R[i, j]) for i in range(num_users)
for j in range(num_items) if R[i, j] > 0 ]
# SGD 기법으로 P, Q 매트릭스를 업데이트 함
for step in range(steps):
for i, j, r in non_zeros:
# 잔차 구함
eij = r - np.dot(P[i, :], Q[j, :].T)
# Regulation을 반영한 SGD 업데이터 적용
P[i, :] = P[i, :] + learning_rate*(eij * Q[j, :] - r_lambda*P[i, :])
Q[j, :] = Q[j, :] + learning_rate*(eij * P[i, :] - r_lambda*Q[j, :])
rmse = get_rmse(R, P, Q, non_zeros)
if step % 10 == 0:
print("iter step: {0}, rmse: {1:4f}".format(step, rmse))
return P, Q
P, Q = matrix_factorization(R, K=3)
pred_matrix = np.dot(P, Q.T)
print(pred_matrix)
[[3.99062329 0.89653623 1.30649077 2.00210666 1.66340846]
[6.69571106 4.97792757 0.97850229 2.98066034 1.0028451 ]
[6.67689303 0.39076095 2.98728588 3.9769208 3.98610743]
[4.96790858 2.00517956 1.00634763 2.01691675 1.14044567]]
6. Surprise 모듈을 활용한 예제
Movielens 데이터를 이용하여 잠재 요인 협업 필터링을 간단히 시연해보도록 하겠다. 본 모듈은 추천 시스템에 널리 쓰이는 대표적인 알고리즘들을 패키지화한 것으로, 사이킷런의 API와 프레임워크와 굉장히 유사하다. 다만 엄격한 Input 체계를 갖추고 있는데, 반드시 사용자 ID, 아이템 ID, 평점만이 포함되어 있는 Row 레벨 형태의 데이터만 Input으로 받아들인다.
# Surprise 패키지: scikit-surprise
from surprise import SVD, Dataset, accuracy, Reader
from surprise.model_selection import train_test_split, GridSearchCV
data = Dataset.load_builtin('ml-100k')
위에서 쓴 load_builtin 메서드는 Movielens 홈페이지에 들를 필요 없이 해당 사이트의 데이터를 다운로드 받고 로드하는 메서드인데, 사실 앞으로 다른 데이터를 쓴다면 크게 쓸 일이 없다. Surprise 모듈은 데이터 로드를 위해 2개의 메서드를 추가적으로 제공한다.
# load_from_file: OS 파일 로딩
ratings = pd.read_csv('data/ratings.csv')
ratings.to_csv('data/ratings_noh.csv', index=False, header=False)
# line_format: 칼럼을 순서대로 나열함. 공백으로 분리
# rating_scale: 평점의 단위
reader = Reader(line_format='user item rating timestamp', sep=',',
rating_scale=(0.5, 5))
data = Dataset.load_from_file('data/ratings_noh.csv', reader=reader)
# load_from_df: Pandas DataFrame 으로 로딩
ratings = pd.read_csv('data/ratings.csv')
reader = Reader(rating_scale=(0.5, 50))
data = Dataset.load_from_df(df=ratings[['userId', 'movieId', 'rating']], reader=reader)
이제 데이터셋을 훈련 데이터와 테스트 데이터로 분할한 뒤 적합을 해보자.
trainset, testset = train_test_split(data, test_size=0.25, random_state=0)
# 알고리즘 객체 생성
# SVD: n_factors(K), n_epochs(디폴트 20), biased=True(베이스라인 사용자 편향 적용 여부)
algo = SVD(n_factors=50, random_state=0)
algo.fit(trainset=trainset)
예측을 위해선 test 메서드와 predict 메서드가 제공되는데, 전자의 경우 테스트 데이터셋 전체에 대한 예측 값을, 후자의 경우 하나의 개체에 대한 예측 값을 출력한다. 따라서 predict의 결과를 모은 것이 test의 결과라고 보면 이해하기 쉽다.
predictions = algo.test(testset=testset)
predictions[0:3]
[Prediction(uid='120', iid='282', r_ui=4.0, est=3.66..., details={'was_impossible': False}),
Prediction(uid='882', iid='291', r_ui=4.0, est=3.97..., details={'was_impossible': False}),
Prediction(uid='535', iid='507', r_ui=5.0, est=4.15..., details={'was_impossible': False})]
# userID, itemID 는 string 으로 입력해야 함
uid = str(196)
iid = str(302)
pred = algo.predict(uid, iid)
print(pred)
user: 196 item: 302 r_ui = None est = 4.30 {'was_impossible': False}
# 정확도 평가
accuracy.rmse(predictions=predictions, verbose=True)
Cross-Validation을 통해 파라미터를 조정할 수도 있다. 코드 구현은 아래와 같다.
#cross_validate(algo=algo, data=data, measures=['RMSE', 'MAE'], cv=5, verbose=True)
algo = SVD()
param_grid = {'n_epochs': [20, 40, 60], 'n_factors': [50, 100, 200]}
grid = GridSearchCV(SVD, param_grid, measures=['RMSE', 'MAE'], cv=3)
grid.fit(data=data)
print(grid.best_score['rmse'])
print(grid.best_params['rmse'])
좀 더 자세한 정보와 다양한 기능에 대해 알아보고 싶다면 아래 공식 문서를 참조하길 바란다.
Reference
파이썬 머신러닝 완벽 가이드, 권철민, 위키북스 카카오 리포트 Surprise 모듈 문서 SVD 설명

