GraphSAGE (Inductive Representation Learning on Large Graphs) 설명
31 Dec 2020 | Machine_Learning Recommendation System Paper_Review목차
본 글에서는 2017년에 발표된 Inductive Representation Learning on Large Graphs란 논문에 대한 Review를 진행할 것이다.
torch_geomectric을 이용하여 GraphSAGE를 사용하는 방법에 대해서 간단하게 Github에 올려두었으니 참고해도 좋을 것이다.
Inductive Representation Learning on Large Graphs Paper Review
1. Introduction
큰 Graph에서 Node의 저차원 벡터 임베딩은 다양한 예측 및 Graph 분석 과제를 위한 Feature Input으로 굉장히 유용하다는 것이 증명되어 왔다. Node 임베딩의 기본적인 아이디어는 Node의 Graph 이웃에 대한 고차원적 정보를 Dense한 벡터 임베딩으로 만드는 차원 축소 기법을 사용하는 것이다. 이러한 Node 임베딩은 Downstream 머신러닝 시스템에 적용될 수 있고 Node 분류, 클러스터링, Link 예측 등의 문제에 도움이 될 수 있다.
하지만 이전의 연구들은 고정된 단일 Graph로부터 Node를 임베딩하는 것에 집중하였는데 실제 현실에서는 새로운 Node와 (sub) Graph가 빠르게 생성되는 것이 일반적이다. (Youtube를 생각해보라!) 고정된 Graph에서 추론을 행하는 것을 transductive한 경우라고 부르고 틀에서 벗어나 새로운 Node에 대해서도 합리적인 추론을 행할 수 있는 경우를 inductive라고 부른다. Node 임베딩을 생성하기 위한 inductive한 접근은 또한 같은 형태의 feature가 존재할 때 Graph 전체에 대해 일반화된 결과를 제공하게 된다.
이러한 inductive Node 임베딩 문제는 굉장히 어렵다. 왜냐하면 지금껏 본 적이 없는 Node에 대해 일반화를 하는 것은 이미 알고리즘이 최적화한 Node 임베딩에 대해 새롭게 관측된 subgraph를 맞추는 (align) 작업이 필요하기 때문이다. inductive 프레임워크는 반드시 Node의 Graph 내에서의 지역적인 역할과 글로벌한 위치 모두를 정의할 수 있는 Node의 이웃의 구조적인 특성을 학습해야 한다.
Node 임베딩을 생성하기 위한 대부분의 기존 접근은 본질적으로 transductive하다. 다수의 이러한 접근 방법들은 행렬 분해 기반의 목적함수를 사용하여 각 Node에 대해 임베딩을 직접적으로 최적화하고 관측되지 않은 데이터를 일반화하지 않는다. 왜냐하면 이러한 방법들은 고정된 단일 Graph에 대해 예측하기 때문이다.
이러한 접근법들은 inductive한 방법에서 작동하도록 수정될 수 있는데, 이를 위해서는 굉장한 연산량이 수반되고 새로운 예측이 만들어지기 전에 추가적인 Gradient Descent 단계를 필요로 한다. 최근에는 Graph Convolution 연산을 이용한 방법들이 논의되었다. 지금까지는 Graph Convolutional Network 또한 transductive한 환경에서만 적용되었다. 본 논문에서 우리는 이 GCN을 inductive unsupervised learning으로 확장하고 단순한 합성곱 이상의 학습 가능한 Aggregation 함수를 사용하여 GCN을 일반화하는 프레임워크를 제안할 것이다.
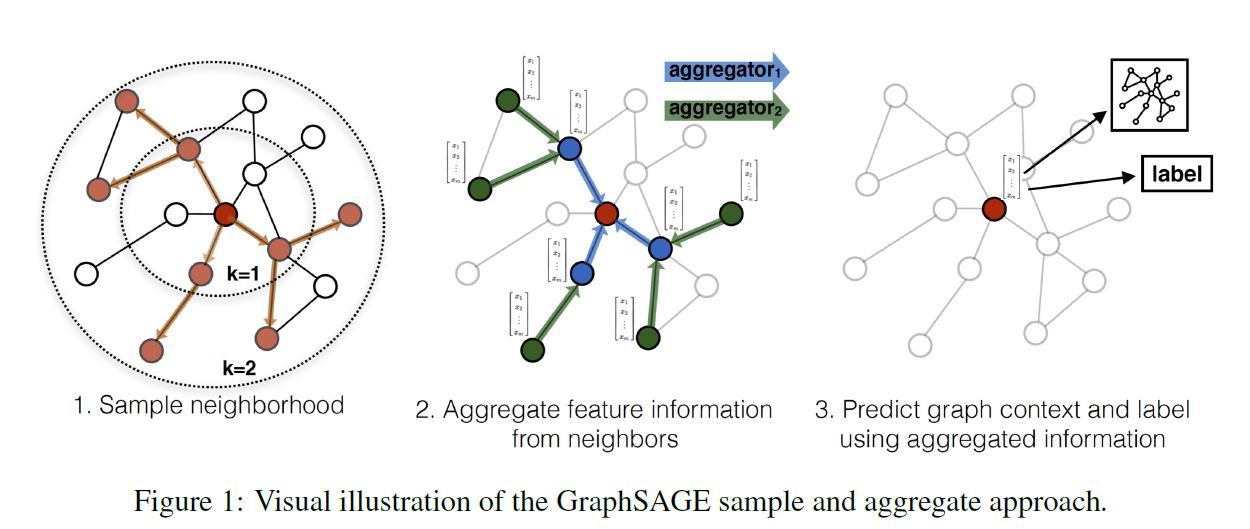
본 논문에서는 Inductive Node Embedding을 위해 일반화된 프레임워크, Graph Sage를 제안한다. 이름은 SAmple과 aggreGatE를 결합하였다. 좀 끼워 맞춘 느낌이 들긴 하다. 행렬 분해에 기반한 임베딩 접근법과 달리 관측되지 않은 Node에서도 일반화할 수 있는 임베딩 함수를 학습하기 위해 Node Feature(텍스트, Node 프로필 정보, Node degree 등)를 Leverage한다. 학습 알고리즘에 Node Feature를 통합함으로써 우리는 이웃한 Node Feature의 분포와 각 Node의 이웃에 대한 위상적인 구조를 동시에 학습할 수 있다. 풍부한 Feature를 가진 Graph에 집중하여 우리의 접근법은 또한 (Node Degree와 같이) 모든 Graph에 존재하는 구조적인 Feature를 활용할 수 있다. 따라서 본 논문의 알고리즘은 Node Feature가 존재하지 않는 Graph에도 적용될 수 있다.
각 Node에 대한 고유의 임베딩 벡터를 학습하는 대신에, 우리는 Node의 지역 이웃으로부터 Feature 정보를 규합하는 Aggregator Function의 집합을 학습한다. 중요한 포인트이다. 왜냐하면 이 컨셉을 통해 각 Node에 귀속된 임베딩 벡터의 한계를 돌파할 수 있기 때문이다.
2. Related Work
논문 참조
3. Proposed method: GraphSAGE
우리의 접근법의 가장 중요한 아이디어는 Node의 지역 이웃으로부터 Feature Information을 통합하는 방법에 대해 학습한다는 것이다. 먼저 1.3.1에서는 GraphSAGE 모델의 파라미터가 이미 학습되어 있다고 가정하고 GraphSAGE의 임베딩 생성 알고리즘에 대해 설명할 것이다. 이후 1.3.2에서는 Stochastic Gradient Descent와 Backpropagation 기술을 통해 모델이 어떻게 학습되는지 설명할 것이다.
3.1. Embedding Generation (i.e. forward propagation) Algorithm
본 섹션에서는 일단 모델의 파라미터가 모드 학습되었고 고정되어 있다고 가정하고 Embedding Generation 혹은 Propgation 알고리즘에 대해 설명할 것이다. 일단 2종류의 파라미터가 있다.
첫 번째는 $K$ 개의 Aggregator Function으로, $AGGREGATE_k, \forall k \in {1, …, K}$ 라고 표현되며, 이 함수는 Node 이웃으로부터 정보를 통합하는 역할을 수행한다.
두 번째는 Weight Matrices의 집합으로, $\mathbf{W}^k, \forall k \in {1, …, K}$ 라고 표현되며, 이들은 모델의 다른 layer나 search depth 사이에서 정보를 전달하는데 사용된다. 다음은 파라미터 학습 과정을 나타낸 것이다.

위에서 확인할 수 있는 직관은 각 iteration 혹은 search depth에서 Node는 그의 지역 이웃으로부터 정보들을 모으고, 이러한 과정이 반복되면서 Node는 Graph의 더 깊은 곳으로부터 정보를 증가시키면서 얻게 된다는 것이다.
알고리즘1은 Graph 구조와 Node Features가 Input으로 주어졌을 때의 임베딩 생성 과정에 대해 기술하고 있다. 아래에서는 Mini-batch 환경에서 어떻게 일반화할 수 있을지 설명할 것이다. 알고리즘1의 바깥 Loop의 각 단계를 살펴보면, $\mathbf{h}^k$ 는 그 단계에서의 Node의 Representation을 의미한다.
첫 번째로, 각 Node $v$ 는 그것의 바로 이웃(Immediate Neighborhood)에 속하는 Node들의 Representation을 하나의 벡터 $\mathbf{h}_{\mathcal{N}(v)}^{k-1}$ 로 합산한다. 이 때 이 합산 단계는 바깥 Loop의 이전 반복 단계(k-1)에서 생성된 Representation에 의존하고 $k=0$ 일 때는 Input Node Feature가 Base Representation의 역할을 하게 된다.
이웃한 Feature 벡터들을 모두 통합한 다음, 모델은 Node의 현재 Representation과 통합된 이웃 벡터를 결합한 뒤 비선형 활성화 함수를 통과시킨다.
\[\mathbf{h}_v^{k-1}, \mathbf{h}_{\mathcal{N}(v)}^{k-1}\]최종적으로 depth $K$ 에 도달하였을 때의 Representation은 아래와 같이 표현할 수 있다.
\[\mathbf{z}_v = \mathbf{h}_v^K, \forall v \in \mathcal{V}\]사실 Aggregator Function은 다양하게 변형될 수 있으며, 여러 방법에 대해서는 1.3.3에서 다루도록 하겠다.
알고리즘1을 Mini-batch 환경으로 확장하기 위해서는 우리는 먼저 depth $K$ 까지 필요한 이웃 집합을 추출해야 한다. 이후 안쪽 Loop(알고리즘1의 3번째 줄)를 실행하는데, 이 때 모든 Node를 반복하는 것이 아니라 각 depth에서의 반복(recursion)을 만족하는데 필요한 Represention에 대해서만 계산한다. (Appendix A 참조)
Relation to the Weisfeiler-Lehman Isomorphism Test
GraphSAGE 알고리즘은 개념적으로 Graph Isomorphism(동형 이성)을 테스트하는 고전적일 알고리즘에서 영감을 얻어 만들어졌다. 만약 위에서 확인한 알고리즘1에서 $K= \vert \mathcal{V} \vert$ 로 세팅하고 Weight Matrices를 단위 행렬로 설정하고 비선형적이지 않은 적절한 Hash 함수를 Aggregator로 사용한다면, 알고리즘1은 Naive Vertex Refinement라고 불리는 Weisfeiler-Lehman: WL Isomorphism Test의 Instance라고 생각할 수 있다.
이 테스트는 몇몇 경우에는 들어맞지 않지만, 여러 종류의 Graph에서는 유효하다. GraphSAGE는 Hash 함수를 학습 가능한 신경망 Aggregator로 대체한 WL Test의 연속형 근사에 해당한다. 물론 GraphSAGE는 Graph Isomorphism을 테스트하기 위해서 만들어진 것이 아니라 유용한 Node 표현을 생성하기 위함이다. 그럼에도 불구하고 GraphSAGE와 고전적인 WL Test 사이의 연결성은 Node 이웃들의 위상적인 구조를 학습하기 위한 본 알고리즘의 디자인의 기저에 깔려 있는 이론적 문맥을 이해하는 데에 있어 큰 도움을 준다.
Neighborhood Definition
본 연구에서 우리는 알고리즘1에서 기술한 것처럼 모든 이웃 집합을 사용하지 않고 고정된 크기의 이웃 집합을 샘플링하여 사용하였다. 이렇게 함으로써 각 Batch의 계산량을 동일하게 유지할 수 있었다.
다시 말해, $\mathcal{N}(v)$ 을 집합 ${u \in \mathcal{V}: (u, v) \in \mathcal{E}}$ 에서 각 반복 $k$ 에서 고정된 크기로 균일하게 뽑은 Sample이라고 정의할 수 있다.
이러한 샘플링 과정이 없으며, 각 Batch의 메모리와 실행 시간은 예측하기 힘들며 계산량 또한 엄청나다.
GraphSAGE의 per-batch space와 time complexity는 $O(\prod_{i=1}^K S_i)$ 로 고정되어 있으며, $S_i, i \in {1, …, K}$와 $K$ 는 User-specified 상수이다.
실제 적용할 때, $K=2$ 와 $S_1 * S_2 <= 500$ 으로 했을 때 좋은 성능을 보였다. (자세한 사항은 1.4.4를 참조)
3.2. Learning the Paremeters of GraphSAGE
완전한 비지도 학습 상황에서 유용하고 예측 능력이 있는 Representation을 학습하기 위해 우리는 Graph 기반의 Loss 함수를 $\mathbf{z}_u, \forall u \in \mathcal{V}$ 라는 Output Represnetation에 적용하고, Weight Matrices $\mathbf{W}^k, \forall k \in {1, …, K}$ 및 Stochastic Gradient Descent를 통해 Aggregator Funciton의 파라미터를 튜닝해야 한다.
Graph 기반의 Loss 함수는 인접한 Node들이 유사한 Representation을 갖도록 하게 하고 서로 멀리 떨어져 있는 Node들은 다른 Representation을 갖게 만든다.
\[J_{\mathcal{G}} = \log (\sigma (\mathbf{z}_u^T \mathbf{z}_v)) - Q \cdot \mathbb{E}_{v_n \sim P_n(v)} \log (\sigma (\mathbf{z}_u^T \mathbf{z}_{v_n}))\]이 때 $v$ 는 고정된 길이의 Random Walk 에서 $u$ 근처에서 동시에 발생한 Node를 의미한다. $P_n$ 은 Negative Sampling Distribution을 $Q$ 는 Negative Sample의 개수를 의미한다.
중요한 것은 이전의 여러 임베딩 방법론에서와는 다르게, Loss 함수에 집어넣는 Representation $\mathbf{z}_u$ 가 Embedding Look-up을 통해 각 Node를 위한 고유의 Embedding을 학습하는 방식으로 형성되지 않는다. Node의 지역 이웃 안에서 포함된 feature로 부터 생성된다. (the representations z are generated from the features contained within a node’s local neighborhood)
이러한 비지도 학습 세팅은 Node Feature가 서비스 혹은 정적인 Repository에 있는 downstream 머신러닝 application에 적용될 때의 상황을 모방하게 된다. 위에서 설명한 Representation이 특정한, 구체적인 downstream task에 이용되어야 할 경우, 앞서 보았던 비지도 Loss는 그 일에 더욱 적합한 (예: cross-entropy loss) 목적함수로 대체되거나 변형될 수 있을 것이다.
3.3. Aggregator Architectures
N차원의 격자 구조 데이터를 이용한 머신러닝 예(텍스트, 이미지 등)들과 달리, Node의 이웃들은 자연적인 어떤 순서를 갖고 있지 않다. 따라서 알고리즘1에서 보았던 Aggregator Function은 반드시 순서가 정해져있지 않은 벡터의 집합에 대해 연산을 수행해야 한다.
이상적으로는 Aggregator Function이 여전히 학습이 가능하고 수준 높은 Representational Capacity를 갖고 있으면서도 대칭적인 형태를 띠고 있으면 좋을 것이다. Input이 순서를 바꿔도 상관 없게 말이다.
Aggregator Funcion의 대칭성은 우리의 신경망 모델이 임의의 순서를 갖고 있는 Node 이웃 feature 집합에도 학습/적용될 수 있게 한다. 본 논문은 이에 대해 3가지 후보를 검증해 보았다.
1) Mean Aggregator
단지 $h_u^{k-1}, \forall u \in \mathcal{N}(v)$ 에 있는 벡터의 원소 평균을 취한 함수이다.
Mean Aggregator는 Transductive GCN 프레임워크에서 사용되는 합성곱 순전파 규칙을 거의 따른다. 특히 우리는 알고리즘의 4~5줄을 다음과 같이 변형하면 GCN의 inductive한 변형 버전을 만들어낼 수 있다.
\[h_v^k \leftarrow \sigma ( \mathbf{W} \cdot mean( \{ h_v^{k-1} \} \cup \{ h_u^{k-1} \} ),\] \[\forall u \in \mathcal{N}(v)\]우리는 위 식이 Localized Spectral Convolution의 개략적인 선형 근사이기 때문에 이를 수정된 평균 기반 Aggregator Convolutional이라고 부를 것이다. (Modified Mean-based Aggregator Convolutional)
2) LSTM Aggregator
앞서 확인한 형태에 비해 조금 더 복잡한 형태의 함수이다. LSTM의 경우 표현력에 있어서 장점을 지니지만 본질적으로 대칭적이지 않기 때문에 permutation invariant 하지 않다.
따라서 본 논문에서는 LSTM을 Node의 이웃의 Random Permutation에 적용함으로써 순서가 없는 벡터 집합에 대해서도 LSTM이 잘 동작하도록 하였다.
3) Pooling Aggregator
Pooling Aggregator는 대칭적이면서도 학습 가능하다. 각 이웃의 벡터는 독립적으로 fully-connected된 신경망에 투입된다. 이후 이웃 집합에 Elementwise max-pooling 연산이 적용되어 정보를 통합한다.
이론 상으로 max-pooling 이전에 여러 겹의 layer를 쌓을 수도 있지만, 본 논문에서는 간단히 1개의 layer 만을 사용하였는데, 이 방법은 효율성 측면에서 더 나은 모습을 보여준다.
계산된 각 피쳐에 대해 max-pooling 연산을 적용함으로써 모델은 이웃 집합의 다른 측면을 효과적으로 잡아내게 된다. 물론 이 때 어떠한 대칭 벡터 함수든지 max 연산자 대신 사용할 수 있다.
본 논문에서는 max-pooling과 mean-pooling 사이에 있어 큰 차이를 발견하지 못하였고 이후 논문에서는 max-pooling을 적용하는 것으로 과정을 통일하였다.
4. Experiments
본 논문에서 GraphSAGE의 성능은 총 3가지의 벤치마크 task에서 평가되었다.
(1) Web of Science citation 데이터셋을 활용하여 학술 논문을 여러 다른 분류하는 것
(2) Reddit에 있는 게시물들이 속한 커뮤니티를 구분하는 것
(3) 다양한 생물학적 Protein-protein interaction 그래프 속에서 protein 함수를 구별하는 것
본 챕터의 경우 논문을 직접 참고하길 바라며, 몇 가지 포인트에 대해서만 정리를 하도록 하겠다.
일단, GraphSAGE의 비교 군으로 총 4가지 방법론이 사용되었다. 완전 무작위, 그래프 구조를 고려하지 않고 raw feature만을 사용한 로지스틱 회귀, DeepWalk 그리고 마지막으로 DeepWalk + raw features, 이렇게 4가지이다.
GraphSAGE도 총 4가지 스타일을 실험하였다. GCN구조, mean aggregator 구조, LSTM aggregator 구조, pooling aggregator 구조 이렇게 4가지이다. vanilla Gradient Descent Optimizer를 사용한 DeepWalk를 제외하고는 모두 Adam Opimizer를 적용하였다. 또한 공평한 비교를 위해 모든 모델은 동일한 미니배치 환경에서 작동하였다.
아래는 테스트 결과이다.
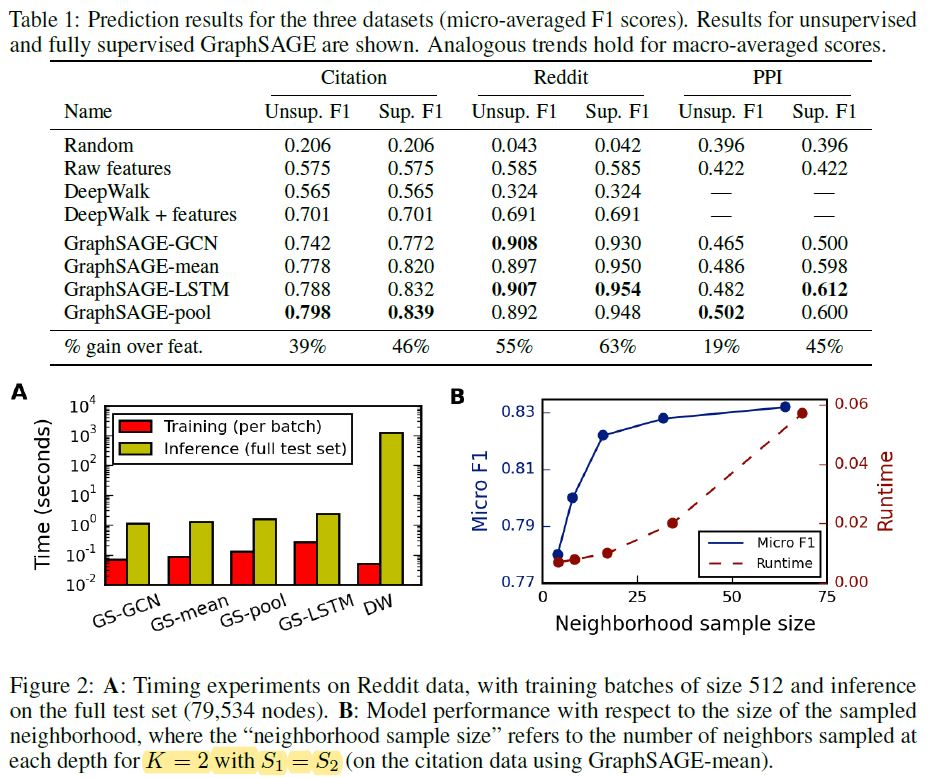
LSTM, Pooling 기반의 Aggregator가 가장 좋은 성능을 보여주었다. K=2로 설정하는 것이 효율성 측면에서 좋은 모습을 보여주었고, 이웃 개체들을 sub-sampling하는 것은 비록 분산을 크게 만들지만 시간을 크게 단축되기 때문에 꼭 필요한 단계라고 할 수 있겠다.
5. Theoretical Analysis
본 Chapter에서는 어떻게 GraphSAGE가 내재적으로는 feature에 의존하면서도 Graph 구조에 대해 학습할 수 있는지에 대해 설명하도록 하겠다.
케이스 스터디의 일환으로, 본 논문에서는 GraphSAGE가 Node의 Clustering Coefficient를 예측할 수 있는지에 대해 알아보았다. Clustering Coefficient는 Node의 지역 이웃들이 얼마나 잘 모여있는지를 측정하는 기준이며 더욱 복잡한 구조적 모티프를위한 토대 역할을 한다.
우리는 GraphSAGE의 임베딩 생성 알고리즘(1.3.1의 알고리즘1)이 Clustering Coefficient를 근사할 수 있음을 증명할 수 있다.
Theorem 1
$x_v$ 가 알고리즘1에서의 feature input을 의미한다고 하자. 모든 Node 쌍에 대해 아래와 같은 조건을 만족하는 고정된 양의 상수 $C$ 가 존재한다고 가정한다.
$K = 4$ 반복 후에 알고리즘1에 대한 파라미터 학습이 이루어졌을 때 $\forall \epsilon > 0$ 에 대해 아래 식이 존재한다.
\[\vert z_v - c_v \vert < \epsilon, \forall v \in \mathcal{V}\]이 때 $z_v$ 는 알고리즘1에 의해 생성된 최종 아웃풋 벡터, 즉 Embedding 벡터이고 $c_v$ 는 Clustering Coefficient을 의미한다.
위 정리는, 만약 모든 Node의 feature가 고유한 값을 가질 때, Graph 속에서 Clustering Coefficient을 근사할 수 있는 파라미터 세팅이 존재함을 의미한다. 이에 대한 증명은 Appendix에서 확인할 수 있다.
증명의 기본적인 아이디어는, 각 Node가 고유한 feature representation을 갖고 있다면 우리는 Node를 indicator 벡터로 연결시키고 이 Node의 이웃을 찾는 방법에 대해 학습할 수 있다는 것이다. 또한 이 증명을 통해 위 정리는 Pooling Aggregator의 몇몇 특징에 의존적임을 밝혔는데, 이를 통해 Pooling을 이용한 GraphSAGE가 다른 GCN이나 Mean-based Aggregator에 비해 더 좋은 성능을 보여준다는 인사이트를 얻을 수 있다.
6. Conclusion
GraphSAGE는 directed 혹은 multi-model graph를 통합하는 것과 같이 무궁무진한 발전 가능성이 있는 모델이다. 최적화를 위해 Non-uniform Neighborhood Sampling 함수를 연구해보는 것과 같이 굉장히 흥미로운 주제들도 남아있다.
Reference
1) 논문 원본
2) 논문 원본 내 참고 사이트
3) 논문 저자 깃헙

