Session-based Recommendation with GNN (SR-GNN) 설명
03 Jul 2021 | Machine_Learning Recommendation System Paper_Review목차
본 글에서는 2018년에 발표된 Session-based Recommendation with Graph Neural Networks라는 논문에 대한 Review를 진행할 것이다. 단순히 논문을 읽어보는 것을 넘어서서, 실제 추천 시스템에서 활용하는 상황을 가정하고 설명을 진행해 볼 것이다.
보통의 세션 기반의 추천 알고리즘의 경우 Recurrent Neural Networks에 기반하여 설계된 경우가 많은데, SR-GNN의 경우 Recurrent Unit과 Graph Neural Network를 결합하여 독특한 형태의 방법론을 제시하고 있다.
세션 기반의 추천 시스템은 익명의 세션에 기반하여 User의 행동을 예측하는 데에 목적을 둔다. 그러나 과거의 여러 연구들을 보면, 세션에서 정확한 User Embedding 벡터를 얻기에는 부족하고 Item 간의 복잡한 transition을 무시하는 경향을 보이곤 했다.
이러한 문제를 해결하기 위해 본 논문에서는 SR-GNN이라는 기법을 제시한다. GNN을 통해 이전의 전통적인 Sequential한 방법들에서는 어려웠던, Item 간의 복잡한 transition을 포착하는 것이 본 방법론의 핵심이다.
Session-based Recommendation with Graph Neural Networks 리뷰
1. Introduction
RNN, NARM, STAMP 등의 여러 방법론이 세션 기반의 추천을 위해 도입되었지만 다음과 같은 한계점을 지닌다. 우선 하나의 세션 내에서 적절한 User 행동이 존재하지 않으면, User Representation을 추정하는데에 어려움을 겪는다는 것이다. 보통 이러한 방법들에서는 RNN의 Hidden Vector가 User Representation으로 취급되는데, 사실 세션은 그 수가 방대하고 충분한 정보가 주어지지 않는다면 세션과 User를 잇기 어렵기 때문에 (익명성) 이러한 방법으로는 각 세션 내에서 User Representation을 추정하기가 쉽지 않은 것이다.
그리고 이전의 연구들에서 분명 Item 간의 transition의 중요성에 대해 밝힌 바는 있으나, 맥락 속에서 발생하는 transition을 무시한 채 단 방향의 transition 만을 고려했다는 문제점을 지닌다.
위 문제점을 해결하기 위해 소개하는 SR-GNN은 Item 사이에서 풍부한 transition을 탐구하고 Item에 대한 정확한 잠재 벡터를 생성할 수 있는 알고리즘이다.
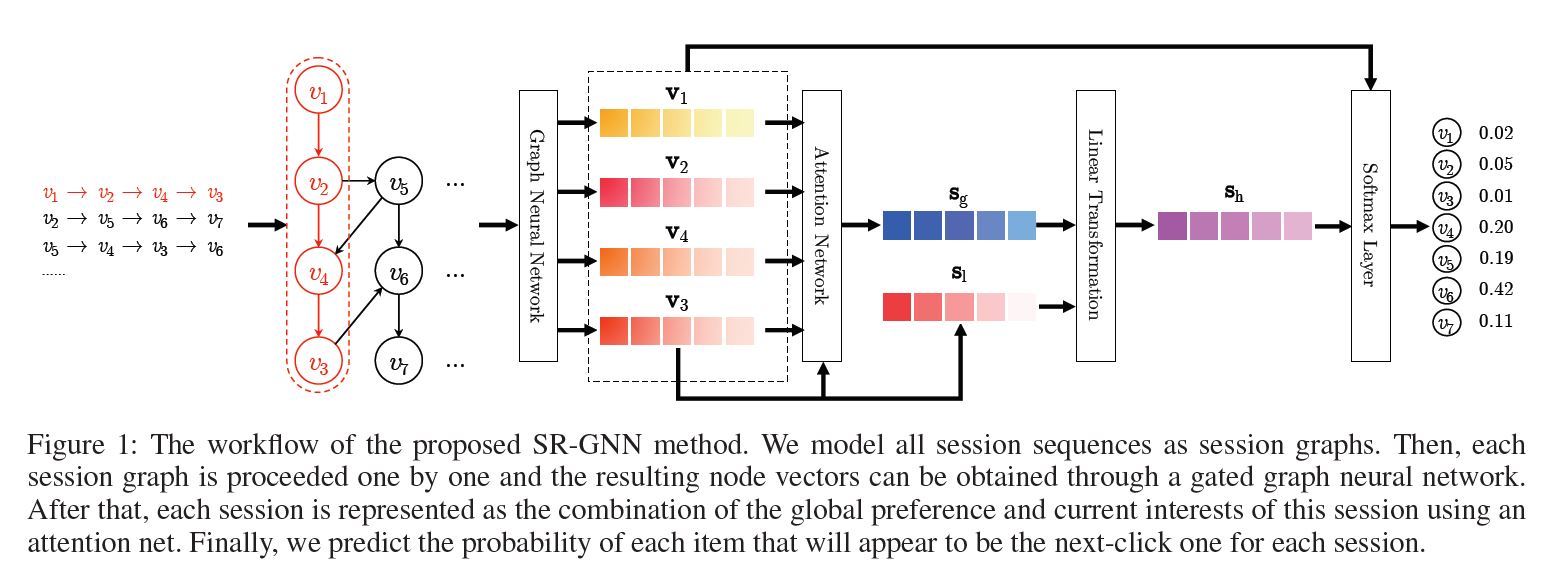
위 그림은 SR-GNN의 구조를 대략적으로 나타낸 것이다. $v_1, …, v_7$ 는 추천 대상인 Item 리스트를 의미한다. 모든 세션 Sequence를 directed session graph로 나타내면, 각 세션 Graph는 하나의 subgraph로 생각할 수 있다. 위 예시에서는 $v_2 \rightarrow v_5 \rightarrow v_6 \rightarrow v_7$ 로 이어지는 하나의 세션을 subgraph로 생각하면 된다.
이제 각 세션은 차례대로 하나씩 위 Workflow을 타고 흐르게 된다. 첫 번째 세션은 $s_1 = [v_1 \rightarrow v_2 \rightarrow v_3 \rightarrow v_4]$ 라고 해보자. 웹사이트나 어플 상의 로그 기록을 기반하여 세션을 구성한다고 하면 위 세션은 어떤 4개의 Item을 순차적으로 클릭한 데이터를 표현한 것이다. 이 세션 데이터는 Gated Graph Neural Network를 통과하여 각각의 Node 벡터를 얻게 된다.
그리고 나서 이를 활용하여 우리는 최종적으로 $\mathbf{s_g}, \mathbf{s_l}$ 이라는 2개의 벡터를 얻게 되는데, 전자는 Global한 선호를 반영하는 Global Session Vector를, 후자는 그 세션 내에서의 User의 현재의 관심을 나타내는, 즉 가장 최근에 클릭/반응한 Item을 나타내는 Local Session Vector를 의미한다.
최종적으로 본 모델은 각 세션에 대해 다음 클릭의 대상자가 될 Item을 예측한다.
2. Related Work
(중략)
3. The Proposed Method
Notations
| 기호 | 설명 |
|---|---|
| $V = [v_1, v_2, …, v_m]$ | 모든 세션에 속해 있는 모든 Unique한 Item의 집합 |
| $m$ | 모든 Unique한 Item의 수 |
| $s = [v_{s, 1}, …, v_{s, n}]$ | 특정 세션 $s$에 속해 있는 Item의 집합, 시간 순서에 의해 정렬됨 |
| $n$ | 특정 세션 $s$에 속해 있는 Item의 수 |
| $v_{s, n+1}$ | 세션 $s$ 에서 다음 클릭의 대상자가 될 Item |
Constructing Session Graphs
전체 Graph는 아래와 같이 정의할 수 있다.
모든 세션 Sequence $s$ 는 아래와 같은 Directed Graph로 정의할 수 있다.
\[\mathcal{G}_s = ( \mathcal{V_s}, \mathcal{E}_s )\]이 세션 Graph에서 각 Item Node는 $v_{s, i} \in V$ 를 나타낸다. 각 Edge $(v_{s, i-1}, v_{s, i}) \in \mathcal{E_s}$ 는 세션 $s$ 에서 $v_{s, i-1}$ 를 클릭한 후에 $v_{s, i}$ 를 클릭했다는 의미이다.
똑같은 Item이 반복적으로 나올 수 있기 때문에 본 논문에서는 각 Edge에 대해 Normalized Weight을 적용하였다. 모델을 통과한 후, 각 Item $v$ 는 Gated GNN을 통과하여 아래와 같이 통합된 Embedding Space에 임베딩되어 Node 벡터로 표현된다.
\[\mathbf{v} \in \mathbb{R^d}\]그리고 각 세션 $s$ 는 Graph에서의 Node 벡터들로 이루어진 $\mathbf{s}$ 라는 임베딩 벡터로 표현된다.
Learning Item Embeddings on Session Graphs
세션 Graph 내에서 이루어지는 Node 벡터의 학습 과정에 대해 알아보자. $t-1$ 시점의 Node 벡터를 활용하여 $t$ 시점의 Node 벡터를 얻게 되는 과정이라고 생각하면 된다. 먼저, 세션 $s$ 내의 $n$ 개의 Node가 주어졌다고 할 때 이들의 Node 임베딩 벡터를 아래와 같이 활용하게 된다.
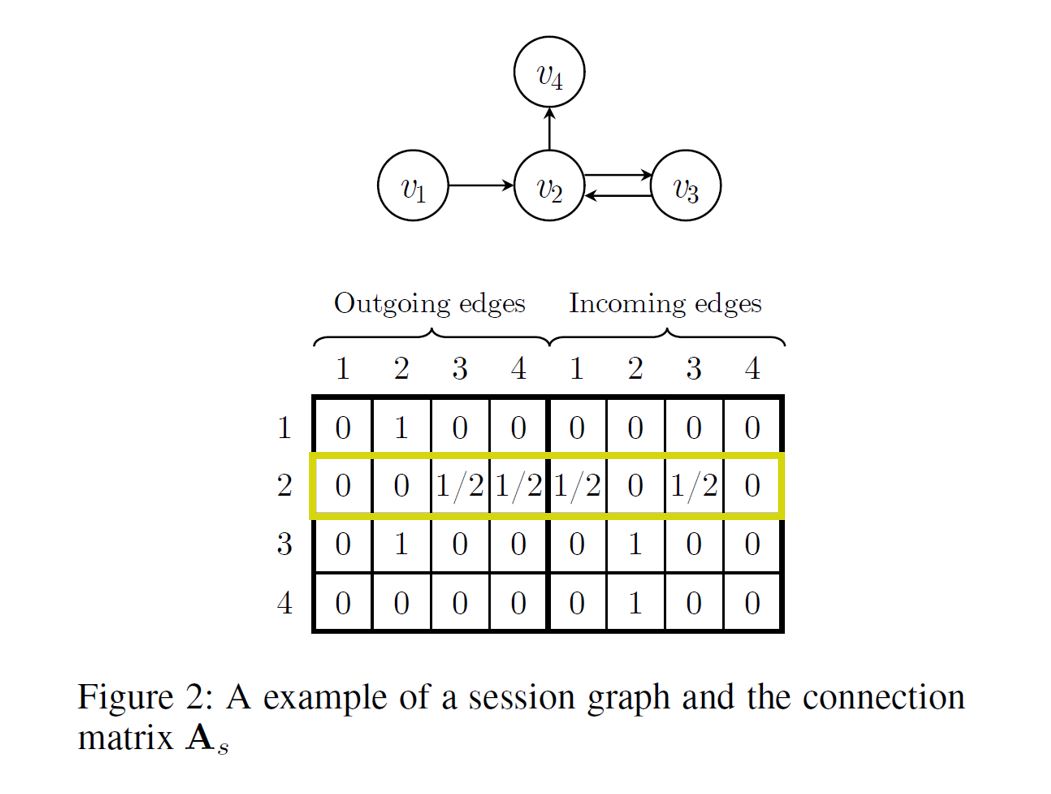
$n=4$ 인 세션을 예로 들어보자. 위와 같은 Subgraph가 있다고 할 때, $\mathbf{A_s}$ 는 위와 같이 표현된다.
이 때 아래 기호로 표기된 Block은
\[\mathbf{A}_{s, i:} \in \mathbb{R}^{1 * 2n}\]다음과 같은 Connection Matrix의 일부이다.
\[\mathbf{A}_{s} \in \mathbb{R}^{n * 2n}\]따라서 형광색으로 표시한 부분이 위 예시에서 $\mathbf{A}_{s, 2:}$ 가 될 것이다.
위 식을 통해 Gated Graph Neural Network를 활용하여 여러 Node 사이의 정보를 전파하는 과정을 수행하게 된다. 이 때 Connection Matrix $\mathbf{A_s}$ 를 통해 현재 관심 있는 Node, 예를 들어 $i=2$ 번째 Node $v_{s, 2}$ 와 관련있는 Row를 추출하여 이후 과정에 활용하게 된다. 즉 Edge가 존재하는 Neighbor들의 정보를 통합하여 $\mathbf{a}_{s, i}^t$ 라는 벡터로 나타내는 것이다. $\mathbf{H}$ 는 Weight를 조절하는 역할을 수행한다. (Parameter)
아래 두 식은 각각 Update Gate와 Reset Gate의 역할을 수행한다. 각각 어떤 정보를 보존하고 어떤 정보를 버릴 것인지를 결정하게 되는 것이다.
이후에는 Candidate State를 아래와 같이 얻게 된다. $t$ 시점, 즉 Current State의 정보를 얼마나 반영하고, $t-1$ 시점, 즉 Previous State의 정보를 얼마나 Reset하는지를 결정하여 Candidate State 값을 얻게 된다.
Final State는 아래와 같이 Previous Hidden State인 $\mathbf{v}_i^{t-1}$ 를 얼마나 Reset하고, Candidate State인 $\widetilde{\mathbf{v}_i^t}$ 를 얼마나 보존하는지를 통해 결정하게 된다.
이렇게 세션 Graph들 내의 모든 Node에 대해 수렴할 때까지 Update를 진행하고 나면 Final Node Vectors를 얻게 된다.
\[\mathbf{v}_1, \mathbf{v}_2, ..., \mathbf{v}_m\]혼란을 방지하고자 다시 언급하면 $i$ 는 Node의 Index를 의미하며, $t$ 는 학습 Update 과정에서의 시점을 의미한다. 모든 업데이트가 끝나면 $t$ 는 필요 없는 기호가 된다.
각 벡터와 행렬의 길이, 차원 등을 정확히 파악하기 위해 아래와 같은 정리 식을 첨부하도록 하겠다.
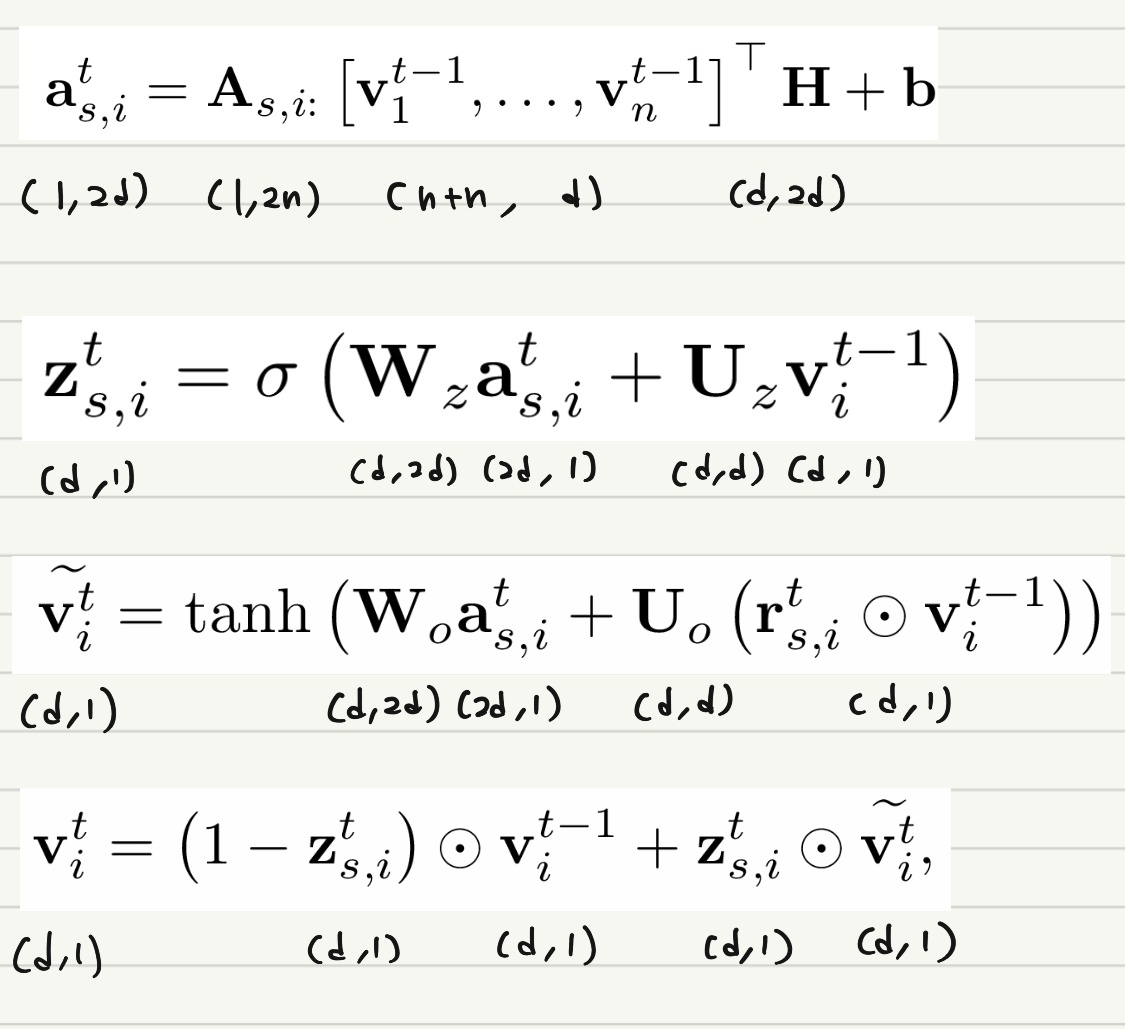
Generating Session Embeddings
지금까지 과정을 통해 모든 세션 Graph를 Gated GNN에 투입하여 모든 Node에 대해 Embedding 벡터를 얻었다. 이제 이렇게 얻은 벡터 값에 기반하여 세션 Embedding을 얻는 방법에 대해 알아보자.
세션 Embedding을 $\mathbf{s} \in \mathbb{R}^d$ 라고 표기하겠다. 이제 이 벡터는 아래와 같이 2가지 벡터를 결합하여 구성할 것이다.
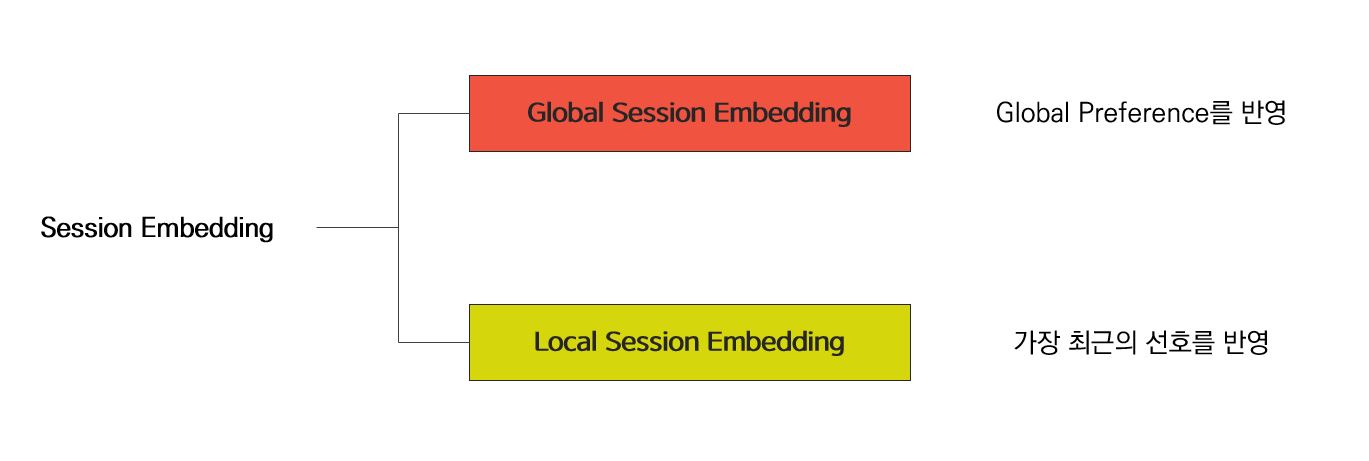
Local Session Embedding은 간단하다. 아래와 같이 가장 최근에 클릭한 Item $v_{s, n}$ 의 Embedding 값을 그대로 쓰면 된다.
해당 세션 Graph $\mathcal{G}_s$의 Global Session Embedding은 모든 Node 벡터를 통합하여 얻을 수 있다. 그런데 이들에 대한 중요도는 각각 다를 것이므로 Soft-attention Mechanism을 사용한다.
식을 보면 Attention Score를 계산할 때 필수적으로 마지막에 클릭한 Item의 Embedding 벡터 값이 고려되는 것을 확인할 수 있다.
이렇게 얻은 두 벡터와 Trainable Parameter Matrix를 활용하여 선형 변환 과정을 거치면 아래와 같이 Hybrid Embedding $\mathbf{s}_h$ 를 얻을 수 있다.
\[\mathbf{s}_h = \mathbf{W}_3 [\mathbf{s}_l, \mathbf{s}_g]\]Making Recommendation and Model Training
추천 후보 Item $v_i \in V$ 가 있다고 할 때 이에 대한 Score $\hat{\mathbf{z}_i}$ 는 아래와 같이 계산된다.
$m$ 개의 Item이 존재한다고 하면 이들 중 가장 높은 Score를 정해야 할 것이다. 이 때는 아래와 같이 Softmax 함수를 사용해준다.
\[\hat{\mathbf{y}} = softmax(\hat{\mathbf{z}})\]다시 한 번 길이, 차원에 대해 정리한다.
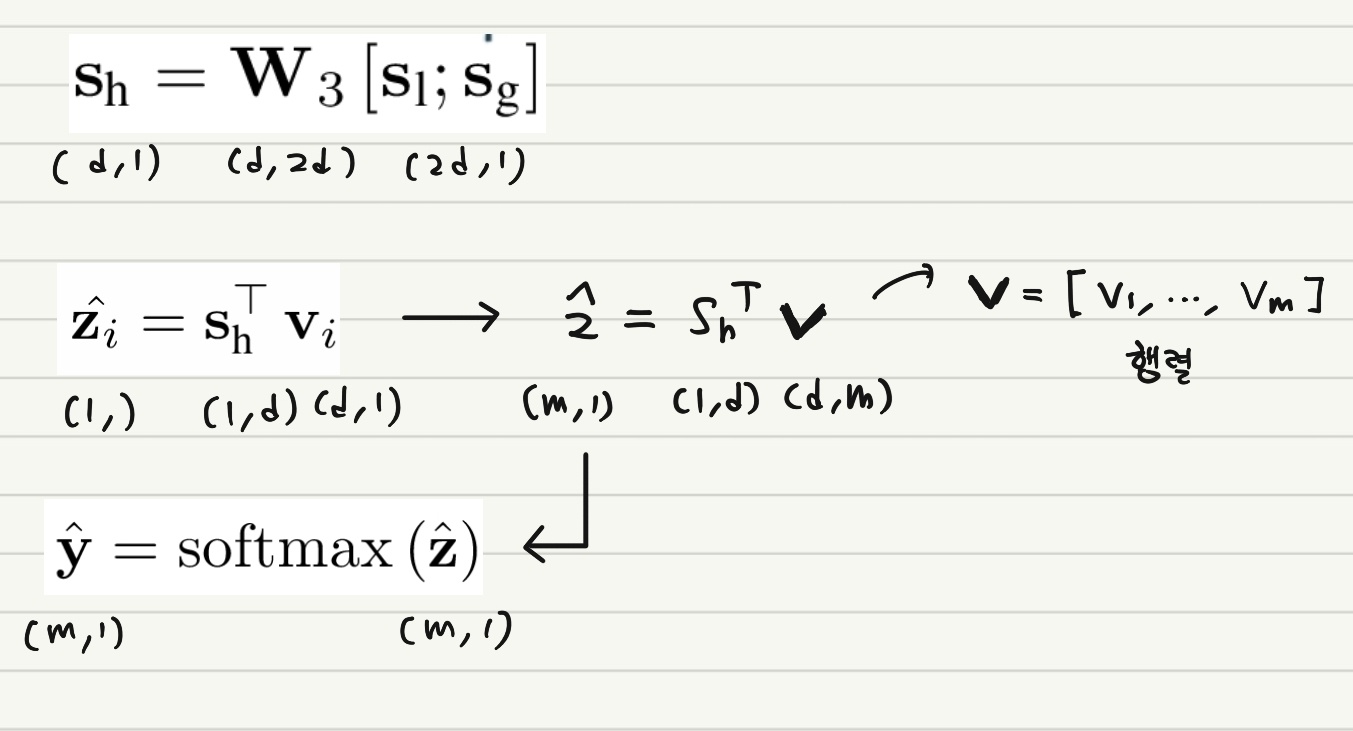
Loss 함수는 아래와 같이 Cross-entropy 함수를 사용해주면 된다.
\[\mathcal{L} (\hat{\mathbf{y}}) = - \Sigma_{i=1}^m \mathbf{y}_i log (\hat{\mathbf{y}}_i) + (1-\mathbf{y}_i) log (1-\hat{\mathbf{y}}_i)\]그리고 이 SR-GNN을 학습하기 위해서는 Back-Propagation Through Time 알고리즘이 사용된다. 일반적으로 세션의 길이는 굉장히 짧기 때문에 과적합을 막기 위해서는 비교적 작은 수의 학습 Epoch이 적용되어야 할 것이다.
4. Experiments and Analysis
본 섹션의 경우 상세 내용에 대해서는 논문 원본을 참조하길 바란다. 다만 세팅과 관련하여 주요 내용만 메모하도록 하겠다.
세션 $s$ 가 아래와 같이 주어져 있다고 하면,
\[s = [v_{s, 1}, v_{s, 2}, ..., v_{s, n}]\]학습을 위해서는 아래와 같이 Sequence를 구성할 수 있다.
$([v_{s, 1}], , v_{s, 2})$, $([v_{s, 1}, v_{s, 2}], v_{s, 3})$ …
Validation Set의 비율은 10%로 설정하였으며 모든 파라미터는 평균0, 표준편차0.1의 정규분포로 초기화하였고, Adam Optimizer가 사용되었다. 최초의 Learning Rate은 0.001이나 3 Epoch마다 0.1의 Decay가 적용되었다. 100의 Batch Size와 $10^{-1}$ 의 L2 페널티가 적용되었다.
5. Conclusions
세션 기반의 추천 시스템은 User의 분명한 선호와 이전의 기록을 얻기 어려울 때 굉장히 유용하다. 본 논문은 Graph 모델을 통해 세션 Sequence를 표현하는 새로운 구조를 제안하였다. SR-GNN을 통해 Item 사이의 복잡한 구조와 transition을 고려할 수 있으며 또한 User의 다음 행동을 예측하기 위해 Long-term 선호와 최근 선호까지 복합적으로 반영하는 전략을 구사할 수 있다.
References
1) 논문 원본

