Graph Diffusion Convolution (GDC) 설명
12 Aug 2021 | Machine_Learning Paper_Review목차
본 글에서는 GDC: Graph Diffusion Convolution의 핵심적인 내용에 대해서 정리해 볼 것이다. 논문 원본을 직접 읽어보는 것을 권하며, 논문의 저자가 작성한 노트북 파일도 참고하면 도움이 된다.
torch_geomectric을 이용하여 GDC를 사용하는 방법에 대해서 간단하게 Github에 올려두었으니 참고해도 좋을 것이다.
Diffusion Improves Graph Learning 설명
1. Background
GNN을 구성하는 데에는 다양한 요소가 존재하지만, Graph Convolution은 가장 핵심적인 부분이라고 할 수 있다. 다양한 형태의 Graph Convolution이 존재하지만 대부분의 경우 직접적인 1-hop 이웃 사이의 관계에서 message가 전달되곤 한다.
본 논문에서는 이러한 제한점을 없애고 spatially localized한 Graph Convolution을 제안하고 있다. GDC는 1-hop 이웃에서만 정보를 모으는 것이 아니라, Diffusion: 확산을 통해 더욱 큰 이웃 집합에서 정보를 통합한다.
즉 GDC는 Graph의 특징을 효과적으로 포착하고 이를 더욱 잘 구조화할 수 있게 Graph를 재정의하는 연산자로 생각하면 된다. 또한 GDC는 특정 GNN에 종속되지 않고 설계 방식에 따라 Graph 기반의 다양한 모델에 적용될 수 있다는 장점을 가진다.
2. Personalized Page Rank
갑자기 왜 주제가 바뀌었는지 의문이 들수도 있지만, PPR은 GDC의 연산 방식을 이해하기 위해서는 반드시 알아야 하는 요소이다.
이후에 설명하겠지만 GDC에는 기존 Graph 내에서 Diffusion을 통해 더욱 넓은 이웃 집합을 형성하고 정보를 통합하는 과정이 있는데, 이 때 가중치 계수로 $\theta_k$ 가 등장하고 이 가중치 계수의 메인 옵션 중 하나가 바로 PPR이다. 본 글에서의 설명은 이 PPR 계수를 중심으로 진행한다. (다른 옵션으로는 Heat Kernel이 있다.)
PageRank 논문 원본은 이 곳에서 확인할 수 있고 이에 대한 좋은 설명을 담은 블로그 글은 이 곳에서 볼 수 있다. 혹은 CS224W 4강에서 자세한 설명을 들어도 좋다.
Graph에서 Node의 중요도를 계산하는 방법에는 여러 가지가 있지만, PPR에서는 이를 다음과 같이 정의한다.
특정 Node $j$ 가 있다고 할 때 이 Node $j$ 를 향하는 Node 들의 중요도의 합이 바로 이 Node $j$ 의 중요도가 된다. 이 때 Node $i$ 에서 밖으로 뻗어 나가는 연결이 3개 존재하고, 이 중 1개가 Node $j$로 향했다고 하면, Node $i$ 가 Node $j$에 기여하는 바는 바로 $\frac{r_i}{3}$ 가 되며 이 때 $r_i$ 는 Node $i$ 의 중요도를 의미한다.
위 설명을 CS224W 강의자료로 확인하면 아래와 같다.
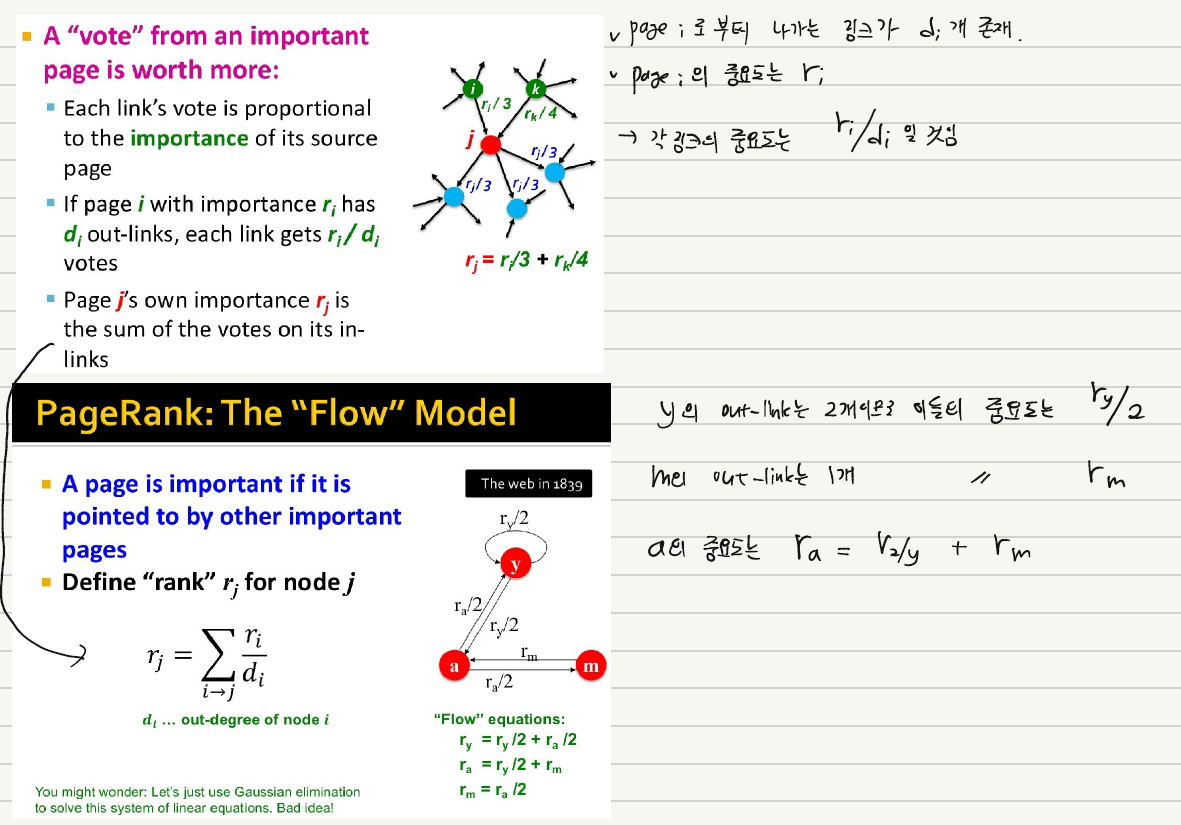

위 설명을 실제로 적용하기 위해서는 아래와 같은 Power Iteration Method를 적용하면 된다.
먼저 초기 중요도 벡터 $\mathbf{r}$ 을 정의한다.
\[\mathbf{r}^0 = [1/N, 1/N, ...]^T\]다음 식을 반복한다.
\[\mathbf{r}^{(t+1)} = \mathbf{M} \mathbf{r}^t\]그리고 위 식이 아래와 같은 조건을 만족할 때 멈춘다.
\[\vert \mathbf{r}^{(t+1)} - \mathbf{r}^t \vert_{1} \le \epsilon\]그런데 이 때 만약 특정 node가 Outbound Link를 가지게 않을 경우 더 이상 업데이트되지 못하고 갇히는 현상이 발생하는데, 이를 위해 일정 확률로 Random 하게 다른 node로 teleport하도록 설정하면 이 문제를 해결할 수 있다.
최종적으로 PageRank 식은 아래와 같이 정의할 수 있다. 아래 식은 node j로 향한 Importance Estimate의 합이 곧 이 node j의 새로운 Importance Estimate임을 의미한다.
\[r_j = \Sigma_{i \rightarrow j} \beta \frac{r_i}{d_i} + (1-\beta) \frac{1}{N}\]위 식의 경우 $\beta$ 의 확률로 link를 따라가고, $1-\beta$ 의 확률로 teleport해야 함을 뜻한다.
위 식을 벡터/행렬화 하면 아래와 같다.
\[\mathbf{r} = \beta M \mathbf{r} + (1-\beta) [\frac{1}{N}]_{N * N}\]여기에서 특정 node를 중심으로 PageRank를 구한 것이 바로 PPR이며 아래와 같이 표현한다.
자 이제 위 식을 GDC 논문에 있는 식에서 사용한 기호로 바꾸기 위해 $1-\beta$ 를 $\alpha$ 로, $M$ 을 $T$로 변환한다.
위 점화식은 아래와 같이 다시 표현할 수 있다.
\[\mathbf{r} = \Sigma_{k=0}^{\infty} \alpha (1-\alpha)^k \mathbf{T}^k\] \[k=0, \mathbf{r} = \alpha \mathbf{a}\] \[k=1, \mathbf{r} = \alpha \mathbf{a} + (1-\alpha) \mathbf{r} \mathbf{T}\] \[k=2, \mathbf{r} = \alpha \mathbf{a} + (1-\alpha) \alpha \mathbf{a} \mathbf{T} + (1-\alpha)^2 \alpha \mathbf{a} \mathbf{T}^2\]그리고 이제 우리는 드디어 PPR 가중치 계수를 얻을 수 있다.
참고로 계산을 위해 위 식을 기하 급수를 이용하여 재표현하면 아래와 같다.
\[r_j = \frac{\alpha} {1- (1-\alpha) r_j}\]3. GDC 수행 과정
지난 Chapter에서 PPR 계수를 구하는 방법에 대해 알았으니 이제는 GDC를 연산하는 과정에 대해 설명할 것이다.
GDC는 아래와 같이 크게 4가지의 과정을 거쳐 수행된다.
1) Transition Matrix $\mathbf{T}$ 를 계산한다. (symmetric 버전)
\[\mathbf{T} = \mathbf{D}^{-\frac{1}{2}} \mathbf{A} \mathbf{D}^{-\frac{1}{2}}\]2) 아래 식을 통해 $\mathbf{S}$를 얻는다.
\[\mathbf{S} = \Sigma_{k=0}^{\infty} \theta_{k} \mathbf{T}^k\]3) 특정 임계 값을 넘지 못하는 작은 값들은 0으로 만듦으로써 위 결과물을 sparsify한다.
(Top-K 방식을 채택할 수도 있다.)
4) 최종적으로 Transition Matrix $\mathbf{T}_{\tilde{\mathbf{S}}}$ 를 계산한다.
\[\mathbf{T}_{\tilde{\mathbf{S}}} = \mathbf{D}^{-\frac{1}{2}}_{\tilde{\mathbf{S}}} \tilde{\mathbf{S}} \mathbf{D}^{-\frac{1}{2}}_{\tilde{\mathbf{S}}}\]정리하자면, 2까지의 과정을 통해 Diffusion을 수행해서 좀 더 넓은 범위를 커버하게 만드는 것이고, 여기서 마치면 새로 계산된 $\mathbf{S}$ 는 Dense Matrix이기 때문에 희소화과정을 통해 중요도가 낮다고 판단되는 값들을 모두 0으로 masking해주는 작업을 3에서 수행한다는 뜻이다.
위 과정 외에도 수식의 완결성을 위한 장치가 여럿 있는데 이는 논문 원본을 참조하길 바란다.
지금까지의 과정을 그림으로 나타내면 아래와 같다.
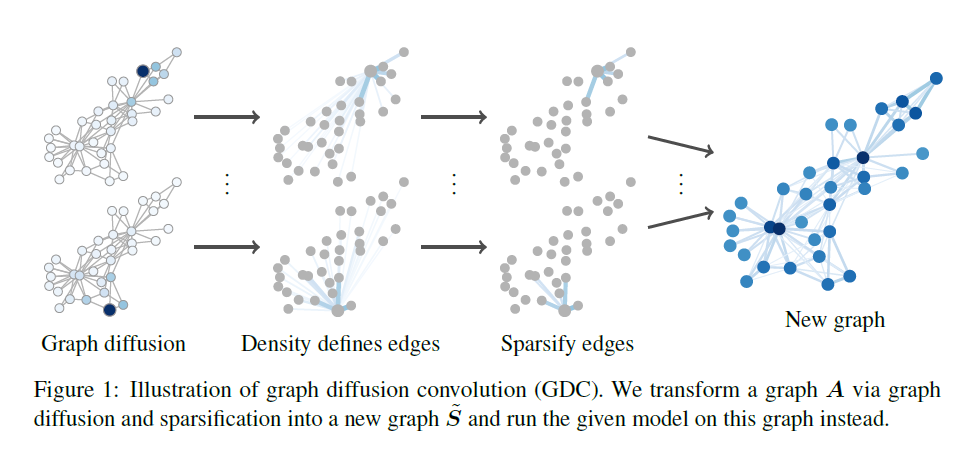
4. 결론
GDC는 spetral한 방법론의 장점을 취하면서도 단점은 취하지 않는다는 특징을 지닌다. GDC가 기초로하는 가정은 homophily(동질성, 연결된 node는 비슷한 성질을 지님)가 만족한다 인데, 이 가정이 통하지 않는 데이터셋에는 경우에 따라 효과적이지 못할 수 있다.
적은 수의 Hyper-parameter를 갖고 있고 응용 범위가 넓기 때문에 다양한 데이터셋과 환경에서 실험 요소로 적극 활용할 수 있을 것으로 보인다.
글 서두의 링크에서도 언급하였듯이 torch_geometric을 통해 적용 방법을 찾는 것이 효율적일 것이다.
References
1) 논문 원본
2) 논문 저자의 깃헙 주소
3) Stanford University CS224W Lecture

