ClusterGCN 설명
15 Aug 2021 | Machine_Learning Recommendation System Paper_Review목차
이번 글에서는 ClusterGCN이란 알고리즘에 대해 다뤄보겠다. 상세한 내용을 원하면 논문 원본을 참고하길 바라며, 본 글에서는 핵심적인 부분에 대해 요약 정리하도록 할 것이다.
torch_geomectric을 이용하여 ClusterGCN를 사용하는 방법에 대해서 간단하게 Github에 올려두었으니 참고해도 좋을 것이다.
Cluster-GCN: An Efficient Algorithm for Training Deep and Large Graph Convolutional Networks 설명
1. Background
Classic Graph Convolutional Layer의 경우 Full-batch 학습이 필연적이었기 때문에 Graph의 크기가 커질수록 메모리 부담이 굉장히 커진다는 단점을 갖는다. Mini-batch SGD를 적용한 알고리즘 또한 Layer가 증가함에 따라 필요한 이웃 node와 임베딩의 수가 급속도로 증가하는 Neighborhood Expansion Problem에서 자유로울 수 없었다. 결국 GCN의 깊이가 깊어질 수록 연산량이 지수함수적으로 증가하는 것이다.
이를 위해 이웃 sample의 수를 고정하는 GraphSAGE, Importance Sampling을 도입한 FastGCN 등이 제안되었지만, 여전히 완전히 문제를 해결할 수는 없었다. VR-GCN 또한 분산 감소 기술을 통해 이웃 Sampling node의 수를 줄였지만, 여전히 메모리 문제에서 자유로울 수 없었다.
본 논문에서는 위와 같은 문제를 해결하기 위해 ClusterGCN이란 알고리즘을 제안한다. ClusterGCN은 METIS라는 Graph Clustering 알고리즘을 통해 Batch Data를 구성하고 이후 이에 적합한 GCN Layer 구조를 취함으로써 효과적으로 Graph 데이터에 대해 학습하게 된다.
ClusterGCN의 경우 오직 현재 Batch에 존재하는 node에 대해서만 임베딩 벡터를 저장하면 되기 때문에 메모리 사용량을 줄일 수 있다. 그리고 복잡한 이웃 Sampling 과정을 필요로 하지 않고 단지 행렬 곱 연산만 수행하면 되기 때문에 구현에 있어서도 편리한 장점을 지닌다.
추가적으로 본 논문에서는 GCN Layer를 더욱 깊게 쌓는 방법에 대해서도 인사이트를 공유한다. (GNN의 경우 Layer를 깊게 쌓는 것이 꼭 긍정적인 결과를 낳지 않으며, 오히려 정교한 설계 없이 Layer를 쌓으면 역효과가 나는 경우가 많다.)
Graph $G = (\mathcal{V}, \mathcal{E}, \mathcal{A})$ 가 존재하고 이 때 node의 수는 $N$ 이며, node feature matrix의 형상은 $(N, F)$ 이다.
다음이 2017년에 발표된 GCN의 기본 update 식임을 기억하자.
\[H^{(l+1)} = \sigma(D^{-1} A H^l W^l)\] \[A^{\prime} = D^{-1}A, H^0 = X\]원 논문에서는 이 식에 대하여 Full Gradient Descent를 이용하게 되는데, 앞서 언급하였듯이 이러한 세팅은 대용량의 현실 데이터에 적합하지 않다. mini-batch SGD를 적용한다면 각 SGD 단계는 아래 Gradient Estimation을 계산하게 될 것이다.
\[\frac{1}{\vert \mathcal{B} \vert} \Sigma_{i \in \mathcal{B}} \triangledown loss (y_i, z_i^{(L)})\]다만 이렇게 진행할 경우 상대적으로 속도가 크게 느려지는 단점이 있다.
2. Vanilla Cluster-GCN
Cluster-GCN의 Batch를 구성하는 아이디어는 어떤 subgraph를 추출하고 이 subgraph에 포함된 node 집합이 $\mathcal{B}$ 이라고 할 때 각 layer의 계산에 필요한 Adjacency Matrix는 $A_{\mathcal{B}, \mathcal{B}}$ 라는 사실에서 출발한다.
그리고 이 때 생성되는 Embedding 벡터들은 위 subgraph 내에서의 관계에 기초하여 구성될 것이다. 그렇다면 Embedding Utilization을 더욱 향상시키기 위해서는 within-batch edges를 최대로 하는 Batch $\mathcal{B}$ 를 만들어 내야 할 것이다.
Graph $G$ 에 존재하는 Node들을 총 $c$ 개로 나눠보자. 이 때 $\mathcal{V}_t$ 는 t번째 파티션에 속해있는 nodes를 의미한다.
\[\mathcal{V} = [\mathcal{V}_1, ..., \mathcal{V}_c]\]이제 우리는 아래와 같이 $c$ 개의 subgraph를 갖게 되었다.
\[\bar{G} = [\mathcal{G}_1, ..., \mathcal{G}_c] = [\{ \mathcal{V}_1, \mathcal{E}_1\}, ...]\]위 규칙에 맞추어 Adjacency Matrix도 나누어보면 아래와 같은 구조를 생각할 수 있다.
\[A = \bar{A} + \Delta = \left[ \begin{matrix} A_{11} & ... & A_{1c} \\ \vdots & \ddots & \vdots \\ A_{c1} & ... & A_{cc} \\ \end{matrix} \right]\] \[\bar{A} = \left[ \begin{matrix} A_{11} & ... & 0 \\ \vdots & \ddots & \vdots \\ 0 & ... & A_{cc} \\ \end{matrix} \right], \Delta = \left[ \begin{matrix} 0 & ... & A_{1c} \\ \vdots & \ddots & \vdots \\ A_{c1} & ... & 0 \\ \end{matrix} \right]\]그러니까 $A_{1c}$ 는 파티션1에 속한 node와 파티션c에 속한 node 사이의 link를 담은 Adjacency Matrix인 것이다.
$\bar{A}$ 와 $\Delta$ 의 가치는 명확히 다르다. 앞서 기술하였듯이 within-link edges를 많이 갖고 있는 Batch를 구성하기 위해서는 $\bar{A}$ 를 잘 구성하는 것이 중요하다고 볼 수 있다.
$\bar{A}$ 를 정규화하면 $A^{\prime} = D^{-1} A$ 가 된다.
최종 Embedding Matrix는 아래와 같이 구성된다.
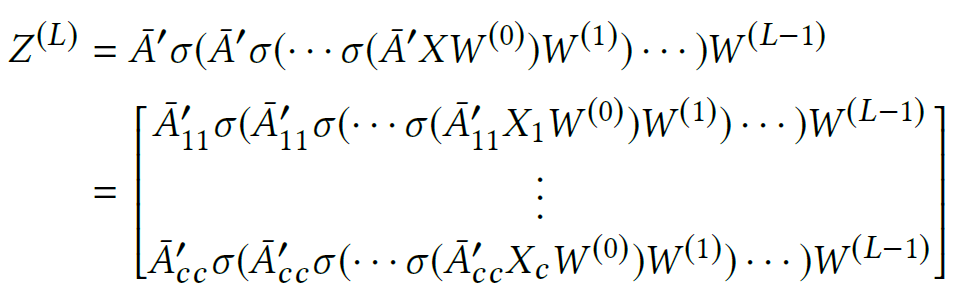
Loss 함수는 아래와 같이 작성할 수 있다.
\[\mathcal{L}_{\bar{A}^{\prime}} = \Sigma_t \frac{\vert \mathcal{V}_t \vert}{N} \mathcal{L}_{\bar{A}^{\prime}_{tt}}, \mathcal{L}_{\bar{A}^{\prime}_{tt}} = \frac{1}{\vert \mathcal{V}_t \vert} \Sigma_{i \in \mathcal{V}_t} loss(y_i, z_i^{L})\]그렇다면 $c$ 개의 그룹으로 나누는 기준은 무엇일까? 본 논문에서는 within-clusters links가 between-cluster links 보다 더 많도록 클러스터를 나누기 위해 METIS라는 Graph 군집화 방법론을 적용했다고 밝히고 있다. 원문은 이 곳에서 확인할 수 있다.
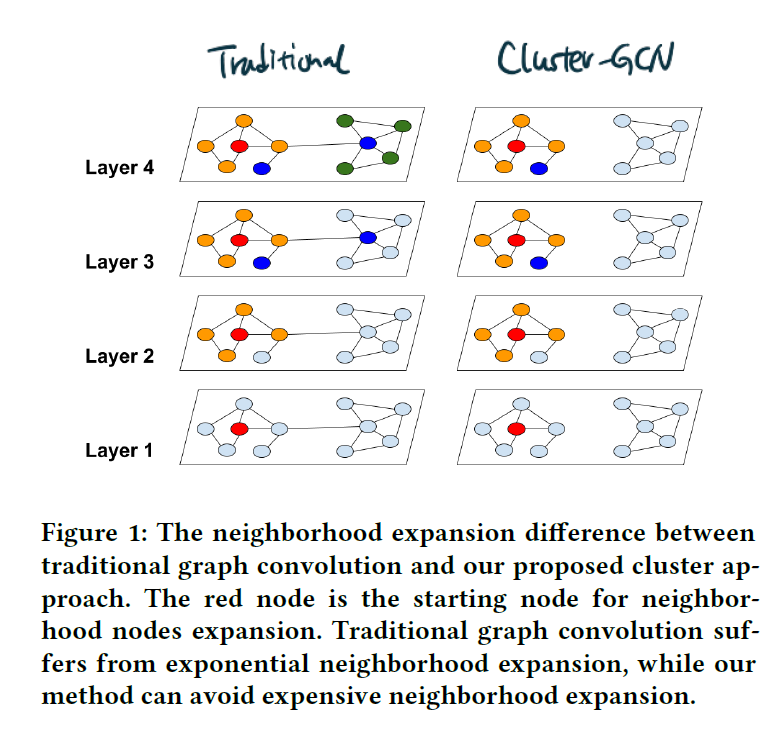
위 그림을 보면 더 깊은 Layer로 진행하면서도 설정한 Cluster의 범위를 벗어나지 않는 ClusterGCN의 특성을 확인할 수 있다.
ClusterGCN의 경우 각 Batch 마다 $\bar{A}^{\prime}_{tt} X_t^{(l)} W^{(l)}$ 와 몇몇 부가적인 계산 만 수행하면 되기 때문에 수행 시간 상의 큰 이점을 누린다. 또한 오직 subraph에 해당하는 부분만 GPU 메모리에 올리면 되기 때문에 메모리 Overhead가 발생할 가능성도 줄어든다.
3. Stochastic Multiple Partitions
이전 Chapter까지의 내용만 보고 ClusterGCN을 적용하려고 하면, 아래와 같이 2개의 문제가 발생한다.
먼저, Graph를 여러 조각으로 쪼개면서 $\Delta$ 에 대한 손실이 발생한다. 이는 데이터 손실이므로 성능에 있어 이슈가 발생할 수 있다.
다음으로 Graph 군집화 알고리즘이 유사한 Node를 모아주므로 Cluster의 분포는 원본 데이터의 분포와는 분명 다를 것이기 때문에, 최종적으로 Full Gradient를 계산하여 반환한 결과물의 경우 bias가 발생할 수 있다.
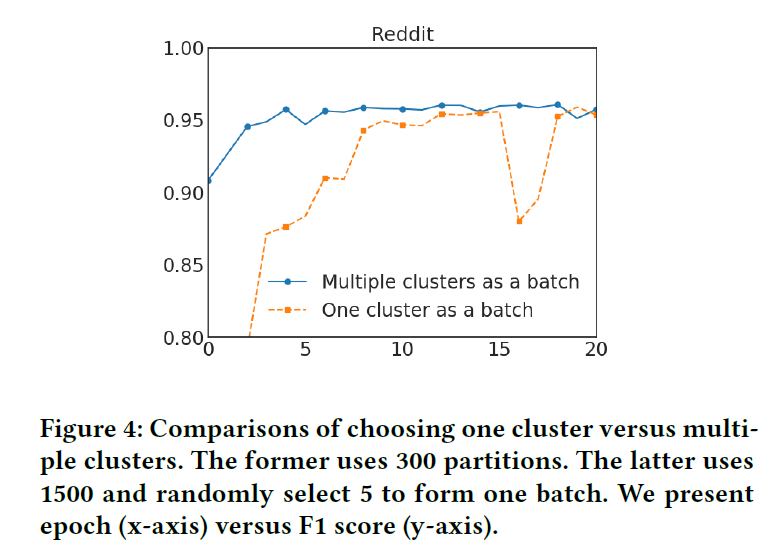
이를 해결하기 위해 Stochastic Multiple Partitions라는 방법론을 도입한다. Graph를 $p$ 개로 나눈다고 하면, 여기서 1개를 선택해서 Batch로 돌리는 것이 아니라 이 중 $q$ 개를 다시 선택해서 이들을 통합한 뒤 하나의 Batch로 취급한다. 즉, 원래 1개만 쓸 것을 여러 개를 합쳐서 쓴다는 의미이다. 이를 통해 Batch 사이의 분산은 줄이면서 between-cluster links는 통합하는 효과를 거둘 수 있다. 실제로 아래 그림을 보면 이와 같은 방법이 효과적이라는 것을 알 수 있다.
4. Issues of training deeper GCNs
본 논문에서는 더욱 깊은 GCN을 학습시키기 위한 간단한 방법을 제시한다. 직관적으로 생각했을 때, 인접한 위치에 있는 node는 멀리 떨어진 node보다 더 큰 영향력을 행사해야 하므로, 각 GCN Layer에서 사용되는 Adjacency Matrix의 대각 원소의 영향력을 더 확대하는 방안이 도입될 수 있다. 즉, 각 GCN Layer의 통합 과정에서 이전 layer에서 넘어온 representation에 더욱 큰 가중치를 부여하는 것이다. 그런데 이 때 그냥 Identity Matrix를 더하면 layer가 증가함에 따라 numerical instability가 지수 함수적으로 커질 수 있기 때문에 이를 고려햐여 아래와 같은 방법이 제안된다.
\[\tilde{A} = (D + I)^{-1} (A + I)\] \[X^{(l+1)} = \sigma ( (\tilde{A} + \lambda diag (\tilde{A})) X^l W^l )\]최종적으로 ClusterGCN 알고리즘을 정리해보면 아래와 같다.

학습 과정과 실험 과정의 경우 논문 원본을 직접 참고하길 바란다. 특징적인 부분은, 실험 데이터셋으로 새롭게 Amazon2M이라는 데이터가 추가적으로 사용되었다는 것이다. 이 데이터 속에서 node는 상품이고, 같은 장바구니에서 구매되었으면 상품 끼리의 link가 존재한다는 설정이 도입되었다.
0.01의 Learning Rate을 가진 Adam Optimizer와 0.2의 Drop Rate, 그리고 512의 Batch Size를 사용했다는 점은 기억해둘 필요가 있으며, 모든 실험은 NVIDIA Tesla V100 GPU (16GB Memory), 20-core Intel Xeon CPU와 192GB의 RAM 환경에서 이루어졌다. Memory 사용량을 확인하기 위해서 Tensorflow의 경우 tf.contrib.memory_stats.BytesInUse(), Pytorch의 경우 torch.cuda.memory_allocated() 함수를 사용하였다고 밝히고 있다.
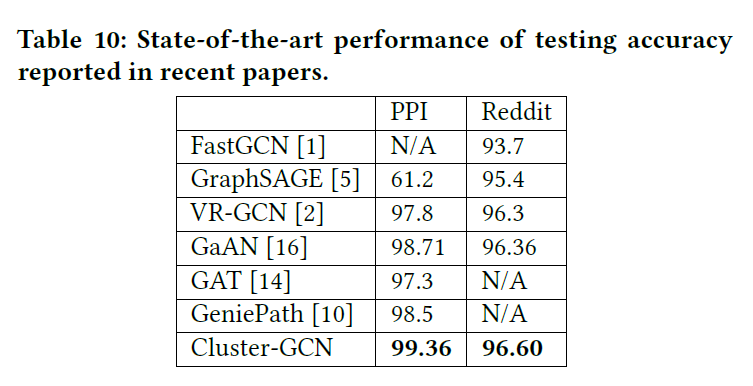
마지막으로 언급할 부분은 구현할 때 고려해야할 부분이다. ClusterGCN이 기반으로 하고 있는 Layer의 경우 $D^{-1}AX$ 를 첫 번째 Layer에서 미리 계산해두면 이후에 재사용함으로써 시간을 크게 절약할 수 있기에 이 부분은 반드시 구현하는 것이 필요하다. 그리고 학습 시에는 테스트용 node의 경우 Adjacency Matrix 및 subgraph에서 아예 제거하고, 최종적으로 Test Performance를 확인할 때 다시 삽입하는 방식으로 진행되었다.
그리고 ClusterGCN은 그 구조적 특징 때문에 새로운 node가 들어오는 Inductive한 예측 환경에서는 유연하게 대처할 수 없다는 한계는 지니고 있다.

