목차

• PREDICT THEN PROPAGATE: GRAPH NEURAL NETWORKS MEET PERSONALIZED PAGERANK 설명
  • 1. Background
  • 2. PPNP 및 APPNP 도출
  • 3. APPNP의 의미
  • 4. 실험 결과와 생각할 부분

이번 글에서는 APPNP란 알고리즘에 대해 다뤄보겠다. 상세한 내용을 원하면 논문 원본을 참고하길 바라며, 본 글에서는 핵심적인 부분에 대해 요약 정리하도록 할 것이다.

torch_geomectric을 이용하여 APPNP를 사용하는 방법에 대해서 간단하게 Github에 올려두었으니 참고해도 좋을 것이다.

PREDICT THEN PROPAGATE: GRAPH NEURAL NETWORKS MEET PERSONALIZED PAGERANK 설명

1. Background

일반적인 GNN에서의 문제점 중 하나는 node에 대해 오직 몇 번의 propagation만 고려되고, 이렇게 커버되는 이웃의 범위를 늘리기가 쉽지 않다는 것이다. 본 논문에서는 GCN과 PageRank의 관계를 이용하여 Personalized PageRank(PPR)에 기반한 개선된 propagation scheme을 구축한다. 결과로 PPNP (Personalized Propagation of Neural Predictions)라는 간단한 모델을 제시하며, 빠르게 근사하는 버전으로 APPNP (Approximate PPNP)를 제시한다.

참고로 PageRank와 본 APPNP 논문과도 관련이 깊은 GDC 논문에 대해서 참고하고자 한다면, 이 글을 확인하길 바란다.

Original PageRank를 변형하여 정의한 Personalized PageRank의 식은 아래와 같은 재귀식으로 표현할 수 있다.

이 때 Teleport 확률 $\alpha$ 는 0~1 사이로 설정된다. 참고로 위 식은 GDC 글에서 기술된 아래 식과 같은 식이다.

위 식을 풀어내면 아래 식을 얻을 수 있다.

indicator 벡터 $i_x$ 는 limit 분포에서도 node의 지역 이웃 정보를 보존하는 역할을 수행한다. 이 벡터를 unit 행렬 $\mathbf{I}_n$ 로 대체하면 최종적으로 fully Personalized PageRank 행렬을 얻을 수 있다.

2. PPNP 및 APPNP 도출

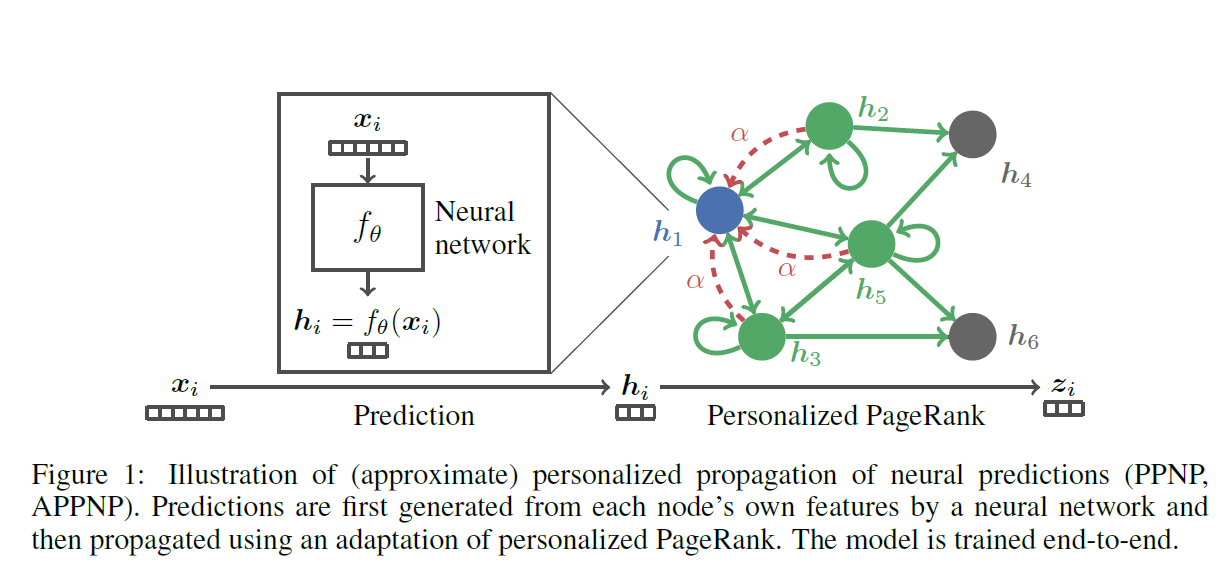
최종 예측값을 도출하기 위해서는 각 node의 feature에 기반하여 예측 값을 생성한뒤 이를 앞서 기술한 fully Personalized PageRank scheme을 통해 전파를 시킨다. 모델 식은 아래와 같다.

이 때, $\mathbf{H}$ 는 Neural Network를 통과한 예측값으로 형상은 (node의 수, class의 수)이다. 물론 softmax를 통해 여러 class에 대한 예측을 수행하는 것이 아니라면 class의 수는 1이 될 것이다.

그런데 위 식을 직접적으로 계산하면 계산 비효율이 발생한다. 이를 해결하기 위해 위해 위 식을 fully PPR 행렬과 Prediction 행렬의 조합으로 보기 보다는, 각 class가 하나의 topic을 구성하는 topic-sensitive PageRank의 변형으로 바라볼 것이다. 이 관점에서 $\mathbf{H}$ 의 모든 칼럼은 teleport set의 역할을 수행하여 nodes에 대한 정규화되지 않은 분포를 정의하게 된다.

PPNP 식을 Power Iteration을 통해 근사하면 APPNP 식을 얻을 수 있다.

위 재귀식을 일정 수준 반복하면 수렴된 값을 얻을 수 있을 것이고, 그 값이 APPNP의 최종 예측값이 된다. 위 재귀식의 수렴성의 증명에 관해서는 본 논문의 Appendix B를 참조하면 된다.

3. APPNP의 의미

지금까지 살펴본 내용에 기반하여 정리한 APPNP의 의미와 특징은 아래와 같다.

• Propgation 부분과 예측값을 생성하는 부분이 분리가 되어있다. 따라서 GNN의 Layer의 수를 늘린다 하더라도 Over-smoothing을 포함한 여러 문제가 나타날 가능성이 낮아진다. 또한 예측값을 생성하는 Neural Network의 구조의 자유도가 높아져 여러 다른 선택지를 고려할 수 있다.
• 모델은 반드시 end-to-end 구조로 학습되어야 한다. 역전파 과정 속에서 Gradient는 Propagation Scheme을 통과하게 되고, 이를 통해 암시적으로 여러 이웃 통합 과정을 고려하게 되는 것이다. 이를 통해 모델의 정확도를 상당 수준 향상시킬 수 있다.
• Propagation에 있어 추가적인 파라미터를 활용하지 않는다.
• Teleport 확률 $\alpha$ 를 통해 이웃 node 끼리 영향을 주는 정도와 범위를 조절하게 된다.

4. 실험 결과와 생각할 부분

본 논문의 실험 결과에는 꽤 흥미로운 부분이 많다. 간단하게만 정리하겠다.

실험에서는 4가지의 text-classification 데이터셋이 사용되었다. (CITESEER, CORA-ML, PUBMED, Microsoft Academic) PPNP 및 APPNP에서 사용되는 Neural Network는 GCN의 구조와 거의 유사하게 설계되었다. (2개의 Layer와 64 hidden size) 첫 번째 Layer에서 $\lambda=0.005$ 의 L2 규제를 적용하였고, Dropout Rate은 0.5를 적용하였다. APPNP의 경우 $\alpha=0.1$, 그리고 Power Iteration의 횟수는 $K=10$ 으로 설정하였다. 자세한 사항은 논문을 참조하길 바란다.

모든 데이터셋에서 PPNP와 APPNP는 대조 모델들을 압도하는 모습을 보였다. 다만 추가적인 행렬 계산의 존재 때문에 속도는 조금 느려졌다는 점은 고려할 필요가 있다. Sparse Label 환경에서 PPNP와 APPNP의 개선 효과는 더욱 돋보였다.

추가적인 실햄에서 APPNP의 경우 아래와 같이 Power Iteration이 늘어날 수록 일반적으로 결과는 향상되는 모습을 보였다.

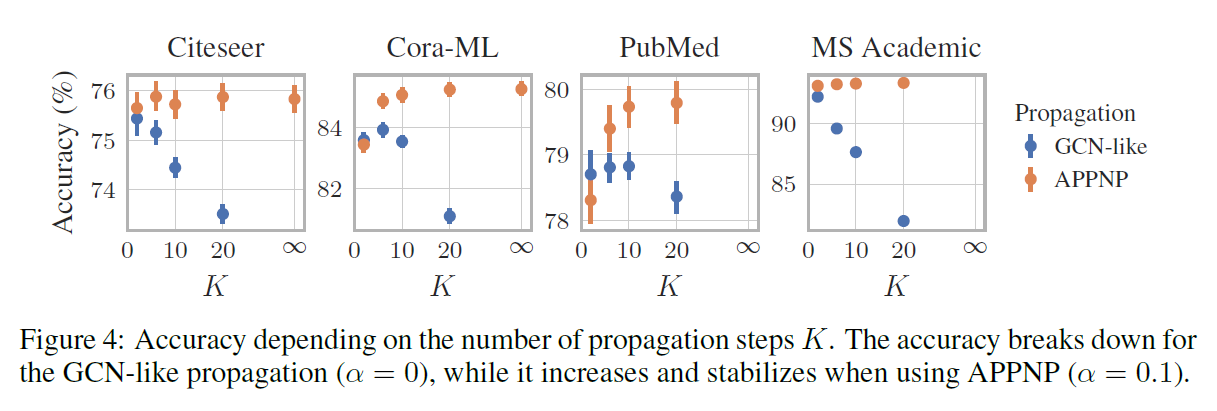
Teleport 확률의 경우 대체적으로 0.05 ~ 0.2 사이에서 좋은 모습을 보였고, 이 값이 증가할수록 수렴 속도는 빨라졌다.

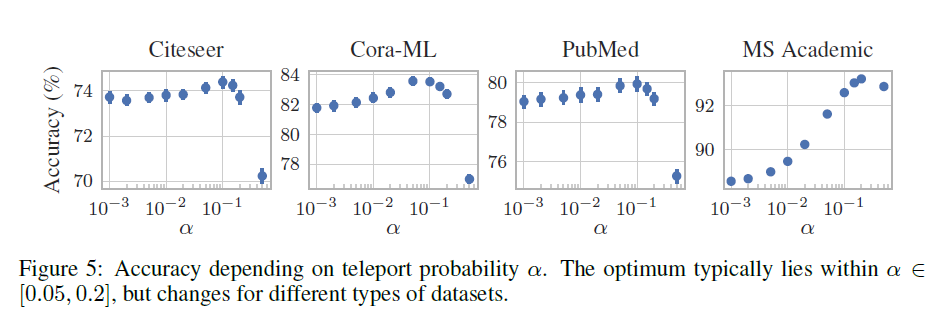
또 하나 재미있는 사실은, 아래 그림에서 확인할 수 있듯이 Training 당시에 Propagation을 생략하고 Inference 과정에서만 Propagation을 진행해도 크게 성능이 떨어지지 않았다는 것이다. 적용되는 데이터에 따라 차이가 있겠지만 이를 통해 APPNP가 Pre-trained된 모델과도 꽤 잘 결합할 수 있을 것이라는 가능성을 엿볼 수 있다.

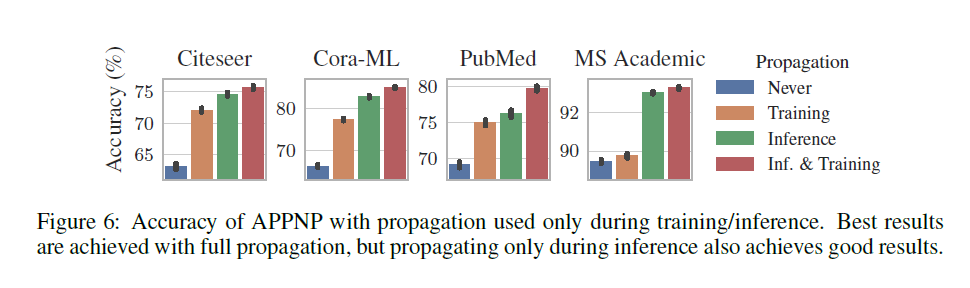
논문에서는 또한 Training 과정에서만 Propagation을 진행했을 때 Propagation을 아예 수행하지 않았을 때에 비해 성능 향상이 크게 이루어졌기 때문에, feature는 존재하나 이웃 정보가 없는 Inductive Learning 상황에서 유용하게 사용할 수 있을 것이라고 언급하고 있는데 이 부분에 대해서는 그 이유가 정확히 파악되지 않는다는 점을 메모로 남긴다.

마무리하자면, APPNP는 기존의 이웃 통합 (Aggregation) 과정에 대해 또 하나의 유용한 선택지를 제공해주었다고 볼 수 있다. 또한 다른 GNN과 결합하여서 사용할 수 있기 때문에 설계 상의 이점이 있고, Power Iteration을 많이 하더라도 파라미터가 증가하지 않고 Gradient가 소실되거나 Over-smoothing 문제가 발생할 가능성이 낮기 때문에 실제 적용하는 데 있어서도 고려해야 할 조건이 적다는 장점을 지닌다.