GTN(Graph Transformer Networks) 설명
08 Sep 2021 | Machine_Learning Recommendation System Paper_Review목차
이번 글에서는 GTN이란 알고리즘에 대해 다뤄보겠다. 상세한 내용은 논문 원본을 참고하길 바라며, 본 글에서는 핵심적인 부분에 대해 요약 정리하도록 할 것이다. 저자의 Gitub에서 코드를 참고할 수도 있다.
Graph Transformer Networks 설명
1. Introduction
대다수의 GNN 연구가 fixed & homogenous graph에 대한 것인 반면, GTN은 다양한 edge와 node type을 가진 heterogenous graph에 대한 효과적인 접근을 위해 고안되었다. heterogenous graph 혹은 relational graph에 대한 연구의 대표적인 예시라고 하면 RGCN을 들 수 있겠는데, GTN은 RGCN과는 다른 방식으로 여러 edge(relation) type을 핸들링한다. 다만 논문에서는 여러 node type에 대해서 분명한 언급을 하고 있지는 않다.
어쨌든 GTN은 모델이 type 정보를 활용하지 못함으로써 suboptimal한 결과를 얻는 것을 방지하기 위해 학습을 통해 복수의 meta-path를 생성하여 다시 한 번 heterogenous graph를 재정의하는 과정을 거치게 된다. 그리고 이후 downstream task에 맞게 GNN layer (논문에서는 classic GCN을 사용)를 붙여서 모델의 구조를 완성한다.
2. Meta-Path Generation
GTN에서의 meta-path는 heterogenous graph에서 여러 edge(relation) type을 부드럽게 조합한 새로운 graph 구조를 생성하는 과정으로 정의할 수 있다.
$t_1, t_2, …, t_l$ 의 edge type이 존재한다고 할 때, 이 특정 edge type에 맞는 인접 행렬은 $A_{t_1}, A_{t_2}, …, A_{t_l}$ 이라고 표현할 수 있다. 이 때 meta-path $P$ 의 인접 행렬은 이들의 행렬 곱으로 이루어진다.
\[A_P = A_{t_1} A_{t_2} ... A_{t_l}\]예를 들어 Author-Paper-Conference 라는 meta-path가 있다고 하자. 그렇다면 이는 아래와 같이 표현할 수 있다.
\[A \xrightarrow{AP} P \xrightarrow{PC} C\]이 meta-path $APC$ 의 인접 행렬은 $A_{APC} = A_{AP} A_{PC}$ 이다.
그렇다면 실제 GTN에서는 meta-path를 어떻게 생성할까.
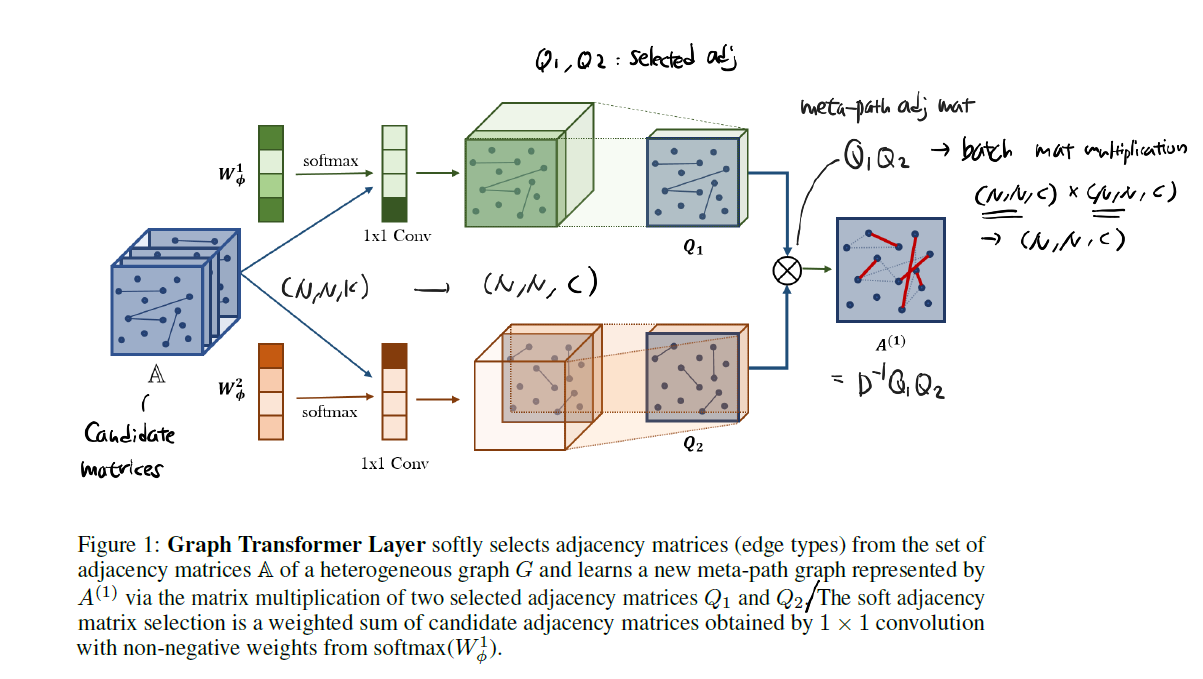
$K$ 개의 edge type이 존재하는 heterogenous graph가 존재할 때, 각 edge type을 분리하여 인접 행렬을 생성한 뒤 이를 겹쳐 놓으면 $\mathbb{A} = (N, N, K)$ 를 구성할 수 있다.
이 때 weight에 softmax 함수를 적용하고 out_channels의 수를 $C$ 개로 설정한 1x1 Convolution 을 적용하면 이 인접 행렬은 $(N, N, C)$ 의 형상을 갖게 된다. 즉 기존의 $K$ 개의 edge type 들이 새로운 방식으로 조합되어 $C$ 개의 relation을 구성하게 된 것이다.
이렇게 2개의 결과를 만들어 낸 것이 $Q_1^1, Q_2^1$ 이고, 이들은 Selected Adjacency Matrices라고 부른다. 즉, 2번에 걸쳐 meta-path를 생성한 것이라고 볼 수 있다. 다시 이들을 곱한 뒤 normalization을 적용해주면 1번째 meta-path 인접 행렬인 $A^1$ 을 얻을 수 있다.
\[A^1 = D^{-1} Q_1^1 Q_2^1\]그리고 짧은/긴 meta-path를 모두 성공적으로 학습하기 위해 $\mathbf{A} = \mathbf{A} + I$ 작업은 추가해준다.
한 번 더 $Q$ 를 만들어 내면 이를 $Q^2$ 라고 명명하고, 이전 결과인 $A^1$ 과 곱하여 $A^2$ 를 생성하게 된다. $l$ 번째로 $Q$ 를 만들어 내면 이 행렬은 $Q^l$ 이 되고, 이전 결과인 $A^{l-1}$ 과 곱하여 최종 결과인 $A^l$ 을 얻게 된다.
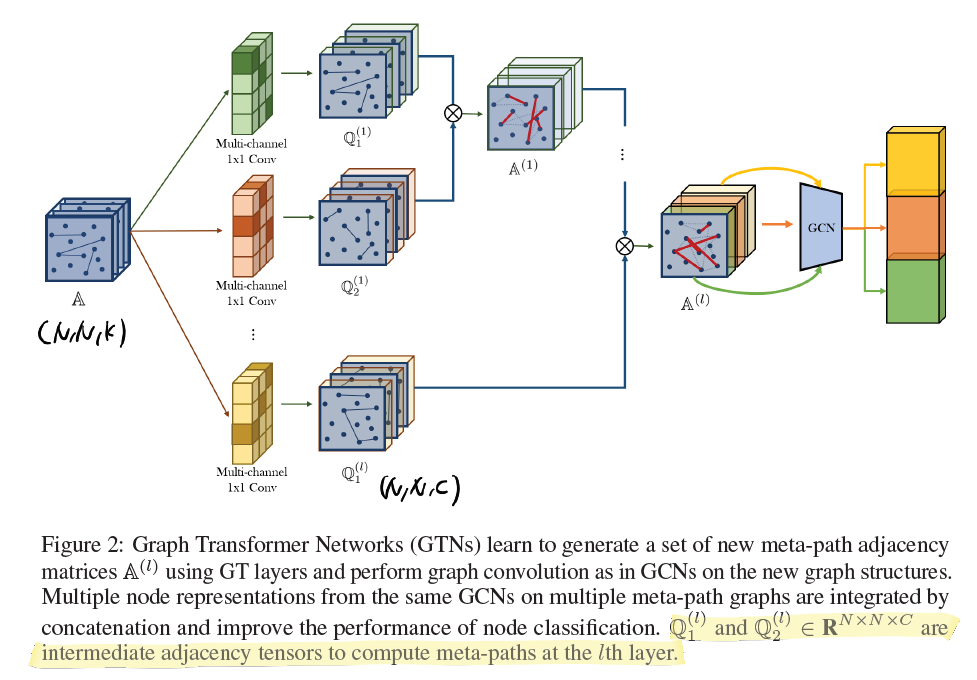
3. Graph Transformer Networks
$l$ 개의 graph transformer layer를 이용했다면 현재 결과인 composite adjacency matrix $A^l$ 은 총 $C$ 개의 새로운 relation에 대한 정보를 포함하고 있을 것이다. 이제 이 행렬을 다시 $C$ 개의 2D 행렬로 분해한 후, 각각에 대해 GNN을 적용한 뒤 concatenation operator를 통해 최종 결과인 $Z$ 행렬을 얻는다.
\[Z = \mathbin\Vert_{i=1}^C \sigma ( \tilde{D}_i^{-1} \tilde{A}_i^l X W )\] \[= [\tilde{D}_1^{-1} \tilde{A}_1^l X W, \tilde{D}_2^{-1} \tilde{A}_2^l X W, ...]\]이 때 $\tilde{D}_i^{-1}, \tilde{A}_i^l$ 는 $(N, N)$, $X$ 는 $(N, d)$, $W$ 는 $(d, d)$ 의 shape을 가진다. 그리고 $W$ 의 경우 모든 channel(new relation)에 대하여 공유되는 trainable parameter이다.
4. Conclusion
실험 결과에 대해서는 논문 원본을 참조하길 바란다.
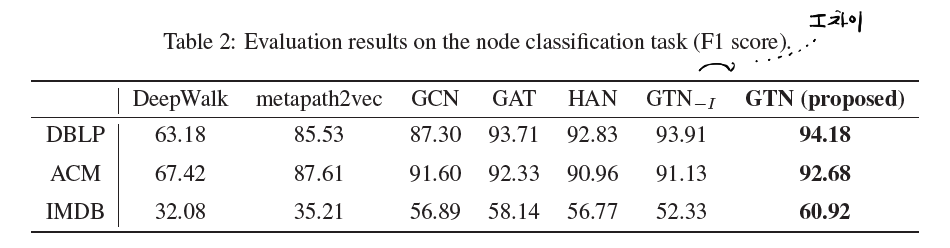
몇 가지 사항을 정리하면서 글을 마무리한다.
1) 1x1 Convolution layer의 weight는 softmax 함수를 적용하여 meta-path를 생성할 때 candidate 인접 행렬에 대한 attention score의 역할을 수행한다. 이를 통해 각 edge(relation) type에 대한 중요도를 가늠해 볼 수 있다.
2) 본 논문에서는 classic GCN을 사용하였지만 task에 따라 다른 GNN layer를 붙여볼 수 있을 것이다. 흥미로운 layer 구성이 많으므로 여러 응용 버전을 기대해 볼 수 있다.
3) GTN은 Full-training에 기반하여 설계되었기 때문에 규모가 큰 graph에 대해서는 수정된 접근이 필요할 것으로 보인다.
4) 본 논문에서는 Embedding Size는 64를 사용하였고, 데이터셋에 따라 다르지만 graph transformer layer는 2~3개 정도를 사용하였다. 데이터셋의 크기가 크지 않아 $C$ 의 크기나 layer의 수 모두 작게 설정하였는데, task에 따라 tuning이 필요할 것으로 보인다.

