목차

• gPool(Graph U-nets) 설명
• DiffPool(Hierarchical Graph Representation Learning with Differentiable Pooling) 설명
• EigenPool(Graph Convolutional Networks with EigenPooling) 설명
• References

본 글에서는 총 3가지의 Graph Pooling에 대해 핵심 부분을 추려서 정리해 볼 것이다. gPool, DiffPool, EigenPool이 그 주인공들이며, 상세한 내용은 글 하단에 있는 논문 원본 링크를 참조하길 바란다.

Github에 관련 코드 또한 정리해서 업데이트할 예정이다.

gPool(Graph U-nets) 설명

graph pooling은 간단하게 말하자면 full graph에서 (목적에 맞게) 중요한 부분을 추출하여 좀 더 작은 그래프를 생성하는 것으로 생각할 수 있다. subgraph를 추출하는 것도 이와 맥락을 같이 하기는 하지만, 보통 subgraph 추출은 그때 그때 학습에 필요한 아주 작은 부분 집합을 추출하는 것에 가깝고, graph pooling은 전체 그래프의 크기와 밀도를 줄이는 과정으로 생각해볼 수 있다.

단순한 그림 예시는 아래와 같다.

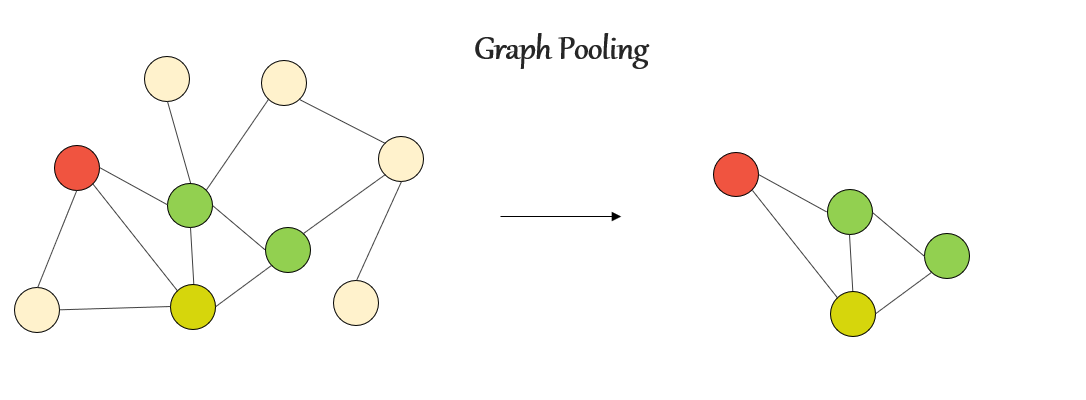
locality 정보를 갖고 있는 grid 형식의 2D 이미지를 다룬 CNN과 달리 그래프 데이터에 바로 pooling과 up-sampling을 수행하는 것은 어려운 작업이다. 본 논문에서는 U-net의 구조를 차용하여 그래프 구조의 데이터에 pooling과 up-sampling(unpooling) 과정을 적용하는 방법에 대해 소개하고 있다.

pooling 과정은 gPool layer에서 수행되며, 학습 가능한 projection 벡터에 project된 scalar 값에 기반하여 일부 node를 선택하여 작은 그래프를 만드는 것이다. unpooling 과정은 gUnpool layer에서 수행되며, 기존 gPool layer에서 선택된 node의 position 정보를 바탕으로 원본 그래프를 복원하게 된다.

모든 node feature는 projection을 통해 1D 값으로 변환된다.

$\mathbf{x_i}$ 는 node feature 벡터이고, 이 벡터는 학습 가능한 projection 벡터 $\mathbf{p}$ 와의 계산을 통해 하나의 scalar 값으로 변환된다. 이 때 $y_i$ 는 projection 벡터 방향으로 투사되었을 때 node $i$ 의 정보를 얼마나 보존하고 있는지를 측정하게 된다. 연산 후에 이 값이 높은 $k$ 개의 node를 선택하면 k-max pooling 과정이 이루어지는 것이다.

참고로 논문에서 모든 계산은 full graph 기준으로 이루어진다. 계산 과정은 아래와 같다.

$\tilde{X}^l$ 이 $(k, C)$ 의 형상을 가졌고, $\tilde{\mathbf{y}}$ 는 $(k, 1)$ 의 형상을, $\mathbf{1}$ 은 $(C, 1)$ 의 형상을 갖고 있다.

$(\tilde{\mathbf{y}} \mathbf{1}_C^T)$ 는 아래와 같이 생겼다.

과정을 그림으로 보면 아래와 같다.

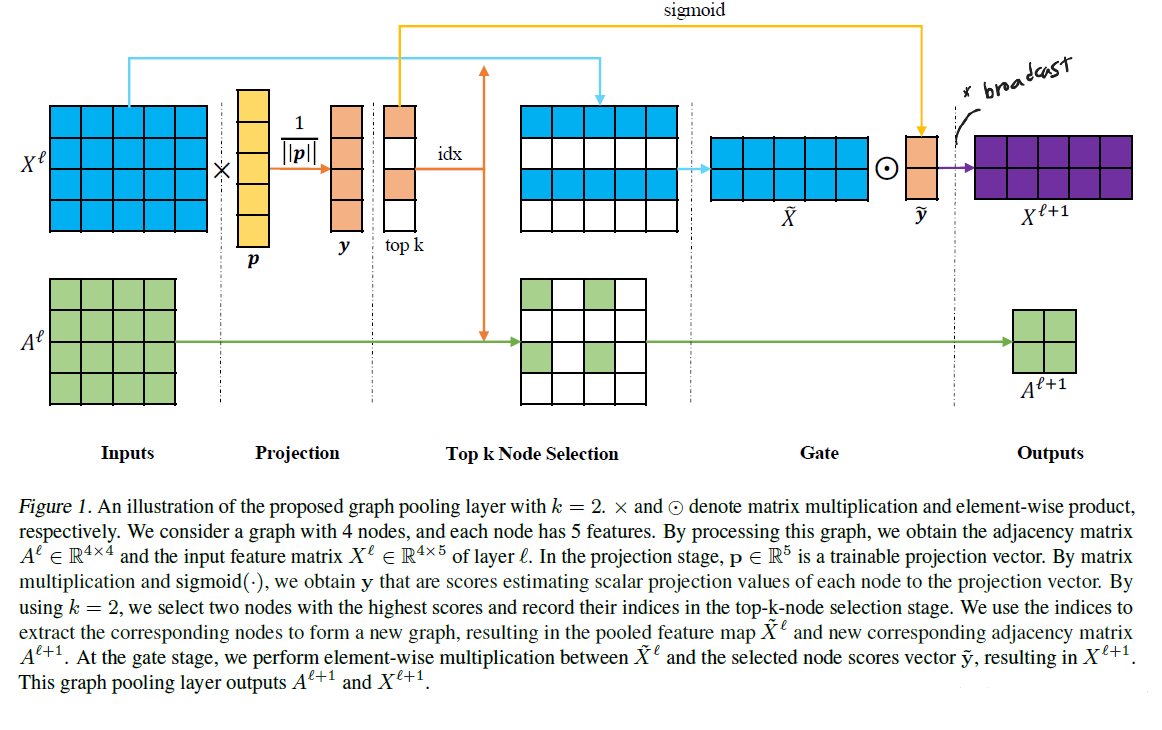
gUnpooling 과정은 아래와 같이 extracted feature 행렬과 선택된 node의 위치 정보를 바탕으로 graph를 복원하는 방식으로 이루어진다.

이렇게 pooling 과정을 진행하다 보면 node 사이의 연결성이 약화되어 중요한 정보 손실이 많이 일어날 수도 있다. 이를 완화하기 위해 논문에서는 Adjacency Matrix를 2번 곱하여 Augmentation 효과를 취한다. 또한 self-loop의 중요성을 강조하기 위해 Adjacency Matrix에 Identity Matrix를 2번 더해주는 스킬이 사용되었다. 2가지 방법 모두 세부 사항을 조금 달리하면서 여러 GNN 논문에서 자주 등장하는 기법이다.

지금까지 설명한 gPooling과 gUnpooling, 그리고 GCN을 결합하면 Graph U-Nets가 완성된다.

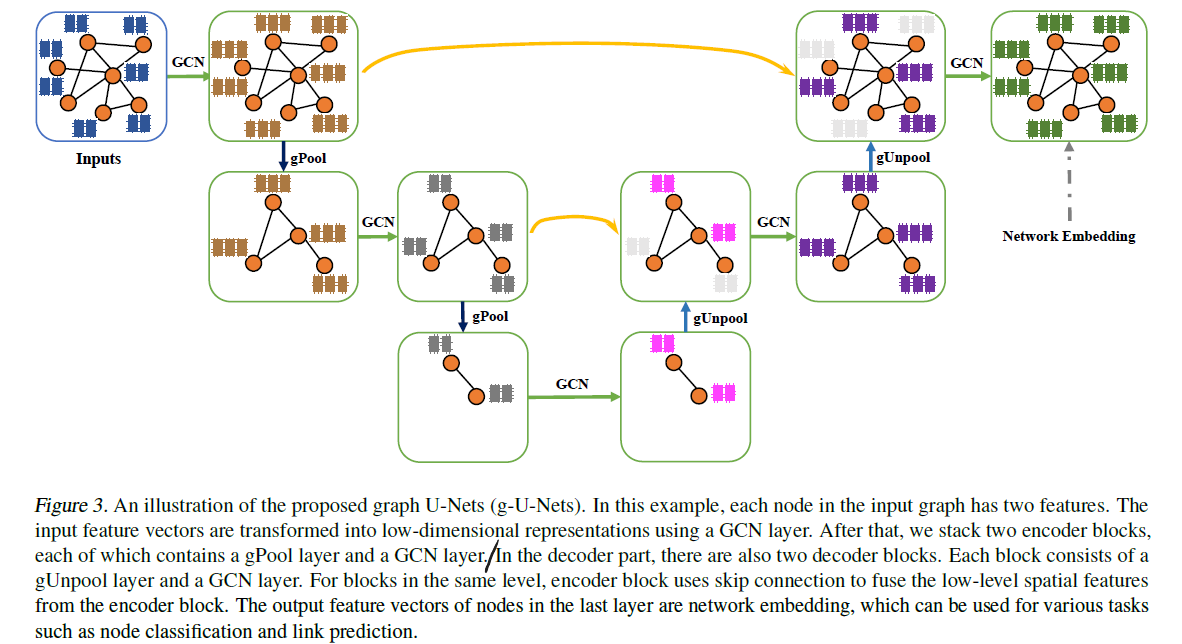
이 모델은 node 분류 및 그래프 분류에서 사용될 수도 있으며, task에 따라 graph에서 중요한 정보를 추출하는 등의 목적으로 사용될 수 있다.

DiffPool(Hierarchical Graph Representation Learning with Differentiable Pooling) 설명

DiffPool 알고리즘은 많은 GNN 모델들이 graph-level classification 문제 상황에서 graph의 계층적 표현 정보를 학습하지 못한다는 한계점을 극복하기 위해 고안되었다. 왜냐하면 대다수의 pooling 방법들은 node embedding을 단순한 합 연산이나 신경망을 통해 globally pool하여 여러 계층 정보의 손실을 야기하기 때문이다.

DiffPool은 미분 가능한 graph pooling 모듈을 의미한다. nodes를 여러 클러스터에 mapping한 후, coarsened input으로 만들어 GNN layer의 input으로 취하는 과정을 통해 DiffPool의 update는 이루어진다. 이 때 클러스터는 input graph에서 잘 정의된 커뮤니티 정도로 생각할 수 있겠다. 이를 그림으로 나타내면 아래와 같다.

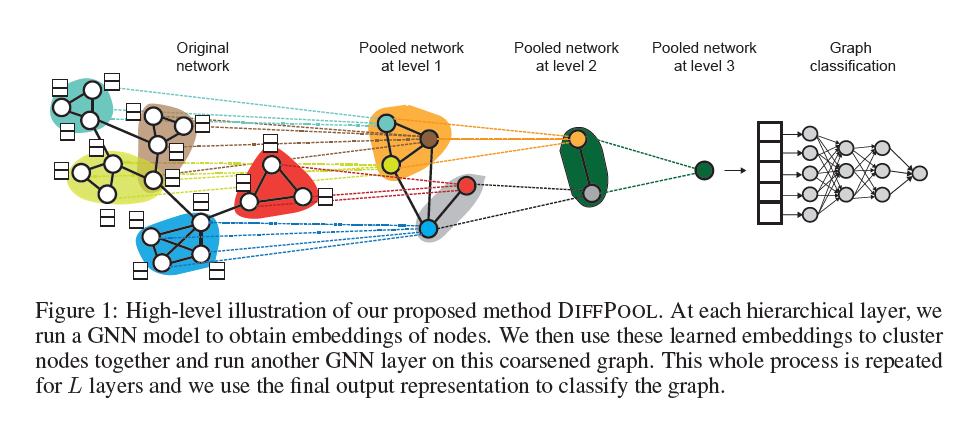
위 그림에서 유추할 수 있듯이, 본 방법론은 여러 GNN과 DiffPool layer를 쌓는(stacking) 방식을 통해 구현된다.

DiffPool에서 가장 중요한 요소 중 하나는 Assignment Matrix이다.

이 행렬은 layer $l$ 에서의 학습된 cluster assignment matrix인데, 이 행렬의 행은 $n_l$ nodes/clusters 중 하나로, 이 행렬의 열은 $n_{l+1}$ clusters의 하나에 해당한다. 즉, 이 행렬을 통해 2개의 layer를 연결하는 셈이다.

node features(embeddings)와 adjacency matrix는 아래와 같이 업데이트된다. 이 과정을 통해 점점 graph의 표현은 거칠어지고 압축되는 효과를 가져올 것이다.

학습은 2개의 구분된 GNN에 의해 이루어진다. 먼저 embedding GNN은 아래와 같다.

논문에서는 GNN으로 GraphSAGE를 사용하였다.

pooling GNN은 아래와 같다.

이 때 softmax는 row-wise 함수이다. 두 GNN은 같은 input을 받지만 구분된 파라미터를 통해 학습한다.

다시 정리하면, $A^l, X^l$ 이 존재할 때, 이를 통해 먼저 $S^l, Z^l$ 을 학습시킬 수 있다. 그러면 이를 바탕으로 $X^{l+1}, A^{l+1}$ 을 업데이트하는 것이다.

최종적으로 1개의 클러스터를 형성하여 graph embedding을 수행하고 downstream task를 수행하게 된다.

논문에서는 2가지 문제점을 밝히고 있다. 일단 연산량이 상당하다는 점이 있는데 이 부분은 추후 연구 주제로 남겨두었다. 두 번째는 수렴이 어렵다는 점이다. 이 부분은 실제 적용에 있어 난제가 될 가능성이 높아 보이는데 논문에서는 이에 대해서 Regularization 항을 추가하는 방안을 제시하고 있다.

이 때 $H$ 는 entropy 함수를 의미한다. 첫 번째는 link prediction objective를 추가한 것에 해당하고, 두 번째는 cluster assignment 행렬의 entropy 항을 추가한 것에 해당한다.

cluster의 수는 node 수의 10% 또는 25% 정도를 사용하였다고 나와있지만, 이 부분의 경우 학습으로 정할 수 있다고 밝히고 있다. cluster의 수가 많으면 계층적 구조를 더욱 잘 모델링할 수 있지만 noise가 발생하고 효율이 떨어질 수 있다고 한다.

EigenPool(Graph Convolutional Networks with EigenPooling) 설명

to be updated…

References

1) gPool 논문 원본
2) DiffPool 논문 원본
3) EigenPool 논문 원본