Metric Learning 설명
06 Dec 2021 | MetricLearning목차
이 글에서는 Metric Learning을 간략하게 정리한다.
Metric Learning
한 문장으로 요약하면,
- Object간에 어떤 거리 함수를 학습하는 task
이다.
예를 들어 아래 이미지들을 보자.



뭔가 “이미지 간 거리”를 생각해보면, 1번째 이미지와 2번째 이미지는 거리가 가까울 것 같다. 이와는 대조적으로, 3번째 이미지는 다른 두 개의 이미지보다 거리가 멀 것 같다.
이런 관계를 학습하는 방식이 Metric Learning이다.
위의 경우는 조금 fine-grained한 경우이고, 좀 더 coarse한 경우는,



1번과 2번 간 거리보다는 3번 간 거리가 훨씬 멀 것 같다.
Training Dataset
그러면, 이러한 관계를 어떻게 데이터셋으로 만들 수 있는가?
- “1번 이미지가 3번 이미지보다는 2번 이미지와 더 가깝다.”
혹은
- 연관도 순으로 1 » 2 » 3 » 4
와 같이 쓸 수도 있고, 어떤 식으로든 관계를 설정해서 데이터셋으로 쓸 수 있다.
그렇다면, 왜 이렇게 복잡해 보이는(?) 방식으로 데이터를 구성하고 학습을 시키는가?
당연히, 이러한 데이터셋은 hard하게 labeling하는 것보다 훨씬 쉽게 대량의 데이터를 구성할 수 있다.
그리고, 위와 같이 어쨌든 supervision이 있기 때문에(좀 약하긴 하지만) metric learning은 지도학습의 일종이다.
Problem Formulation
크게 3가지로 생각할 수 있다. 이 중 일반적으로 2번째가 많이 쓰인다.
- Point-wise Problem: 하나의 학습 샘플은 Query-Item 쌍이 있고 어떤 numerical/ordinal score와 연관된다.
- 그냥 classification 문제와 비슷하다. 하나의 query-item 쌍이 주어지면, 모델은 그 score를 예측할 수 있어야 한다.
- Pair-wise Problem: 하나의 학습 샘플은 순서가 있는 2개의 item으로 구성된다.
- 모델은 주어진 query에 대해 각 item에 점수(혹은 순위)를 예측한다. 순서는 보존된다.
- 그 순위(순서)를 최대한 바르게 맞추는 것이 목표가 된다.
- List-wise Problem: 하나의 학습 샘플이 2개보다 많은 item의 순서가 있는 list로 구성된다.
- 계산량이 많고 어려워서 많이 쓰이지는 않는다.
- NDCG 등으로 평가한다.
NDCG(Normalized Discounted Cumulative Gain)
널리 쓰이는 ranking metric(순위 평가 척도)이다.
먼저 CG를 정의한다.
Cumulative Gain: result list에서 모든 result의 관련도 점수의 합. $rel_i$는 관계가 제일 높으면 1, 그 반대면 0이라 할 수 있다. 물론 0~1 범위가 아니라 실제 점수를 쓸 수도 있다.
\[\text{CG}_p = \sum^p_{i=1}rel_i\]이제 DCG를 정의하자. Discounted CG는 상위에 있는 item을 더 중요하게 친다.
\[\text{DCG}_p = \sum^p_{i=1} \frac{rel_i}{\log_2(i+1)} = rel_1 + \sum^p_{i=2} \frac{rel_i}{\log_2(i+1)}\]Alternative formulation of DCG를 생각할 수도 있다. 이는 관련도상 상위 item을 더 강조한다.
\[\text{DCG}_p = \sum^p_{i=1} \frac{2^{rel_i}-1}{\log_2(i+1)}\]그런데 DCG는 개수가 많거나 관련도 점수가 높으면 한없이 커질 수 있다. 그래서 정규화가 필요하다.
이제 Normalized DCG를 정의하자. 그러러면 먼저 Ideal DCG를 생각해야 한다. IDCG는 위의 식으로 최상의 결과를 출력했을 때 얻을 수 있는 점수라 생각하면 된다.
\[\text{DCG}_p = \sum^{REL_p}_{i=1} \frac{rel_i}{\log_2(i+1)}\]이제 NDCG는 다음과 같다.
\[\text{NDCG}_p = \frac{DCG_p}{IDCG_p}\]Triplet Loss
3개의 point 간 거리를 갖고 loss를 구하는 방식이다.
- 기준점을 Anchor,
- anchor와 관련이 높은 point를 Positive,
- 관련이 없거나 먼 point를 Negative
라 하면,
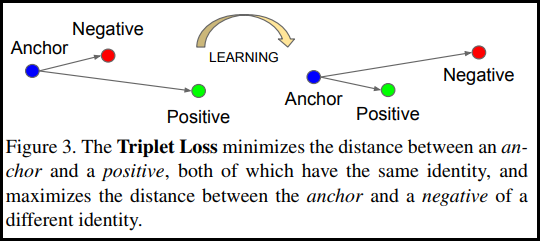
loss function은 유클리드 거리 함수로 생각할 수 있다.
\[\mathcal{L}(A, P, N) = max(\Vert \text{f}(A) - \text{f}(P) \Vert^2 - \Vert \text{f}(A) - \text{f}(N) \Vert^2 + \alpha, 0)\]$N$개의 anchor point로 확장하면 다음과 같이 쓸 수 있다. (사실 같은 식이라 다름없다)
\[\mathcal{L} = \sum^N_i [ max(\Vert \text{f}(x_i^a) - \text{f}(x_i^p) \Vert^2 - \Vert \text{f}(x_i^a) - \text{f}(x_i^n) \Vert^2 + \alpha, 0)]\]$\alpha$는 margin을 나타낸다.
Training(Dataset)
학습할 때 anchor과 positive, negative를 잘 설정해야 한다.
랜덤으로 point를 뽑으면 잘 되지 않는 경우가 많다.
여기서 사용할 수 있는 방법으로 Online Negative Mining이 있다.
이는 batch를 크게 잡아서, 현재 sample인 anchor-positive-negative에서 다른 sample의 anchor/positive/negative 중 anchor와 positive 관계인 것을 제외하고 가장 가까운 것부터 선택하여 negative를 대체하여 계산할 수 있다. 이러면 학습이 조금 더 되지만, batch size가 커야 되고, 계산량이 매우 많아지는 단점이 존재한다.
학습을 더 잘 하기 위해서 생각해야 할 방법은 semi-hard negative mining이다.
A와 P는 고정이라 할 때, 아래 3개의 Negative 중 어느 것을 선택해야 학습이 잘 될까라는 문제이다.
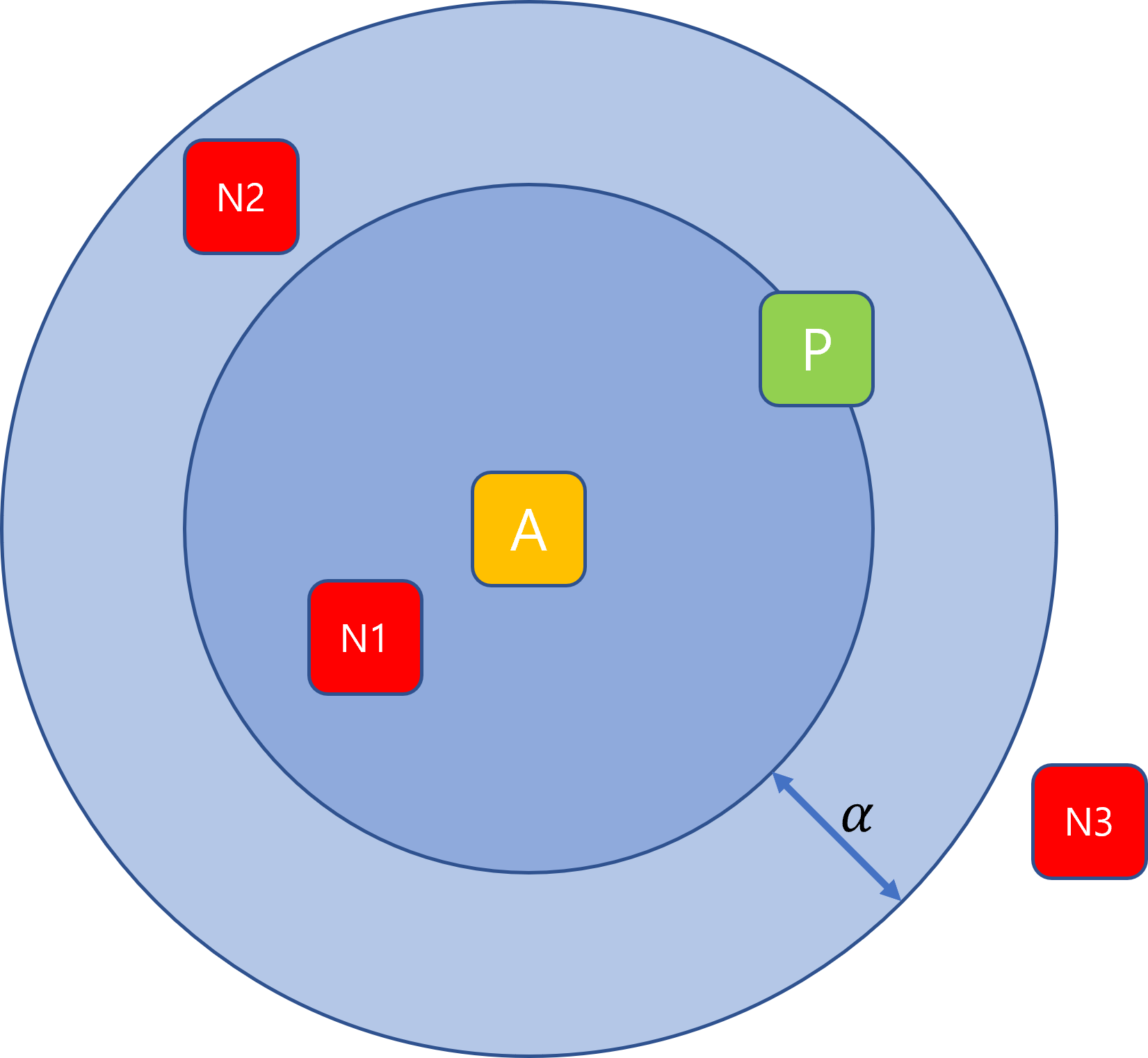
- Hard Negative: $d(a, n_1) < d(a, p)$
- 언뜻 보면 학습이 잘 될 것 같지만, loss를 줄이는 방법은 그냥 모든 $x$에 대해 $f(x)=0$으로 만들어 버리는 것이라(collapsing) 학습이 잘 안 된다.
- Semi-hard Negative: $d(a, p) < d(a, n_2) < d(a, p) + \alpha$
- 이 경우에는 위의 collapsing problem이 발생하지 않으면서 N을 P 밖으로 밀어내면서 학습이 제일 잘 된다.
- Easy Negative: $d(a, p) + \alpha < d(a, n_3)$
- N3는 이미 $d(a, p) + \alpha$보다 멀리 있기 때문에 negative로 잡아도 학습할 수 있는 것이 없다.
따라서 semi-hard negative로 sample을 잡아 학습하는 것이 제일 좋다고 한다.
FaceNet: A Unified Embedding for Face Recognition and Clustering
논문 링크: FaceNet: A Unified Embedding for Face Recognition and Clustering
Metric Learning을 사용해서 여러 사진이 있을 때 같은 사람의 사진끼리 모으는 task를 수행했다.

