Graphormer(Do Transformers Really Perform Bad for Graph Representation?) 설명
30 Jan 2022 | Machine_Learning Recommendation System Paper_Review목차
이번 글에서는 Transformer가 정말로 그래프 데이터에 잘 적용될 수 있는지에 대해 고찰하고, Graphormer라는 더 나은 접근을 제시한 논문에 대해 다뤄보겠습니다.
논문 원본은 이 곳에서 확인할 수 있으며, 깃헙도 참고할 수 있습니다.
본 글에서는 핵심적인 부분에 대해서만 살펴보겠습니다.
Graphormer: Do Transformers Really Perform Bad for Graph Representation? 설명
1. Introduction
Transformer의 유용함은 자명한 사실이지만 이를 그래프 데이터에서도 잘 활용할 수 있는가에 대해서는 완전한 확답을 찾지는 못한 상황입니다. 여러 연구에서 이를 시도하긴 하였지만 충분하지는 않았습니다. Transformer는 본래 sequence modeling을 위해 설계되었는데 그래프의 구조적인 정보를 모델에 잘 반영해야지만 이를 잘 활용할 수 있을 것입니다.
node에 반영된 그래프의 구조적인 정보와 node 쌍 사이의 관계 등을 제대로 고려하지 않은 상태에서 Self-attention을 사용하는 것은 단지 node 간의 semantic similarity를 계산하는 것에 그칠 뿐입니다. 즉 오로지 feature의 특성으로 attention이 적용될 것입니다.
이를 해결하기 위해 논문에서는 Centrality Encoding과 Spatial Encoding을 제안하고 있습니다. 이 구조에 대해서는 아래에서 자세히 설명하겠습니다.
본 글에서는 그래프 네트워크의 일반적인 부분에 대해서 설명하지는 않겠습니다. 이 내용에 대해서는 이전 글들을 보시면 좋습니다.
2. Model Architecture
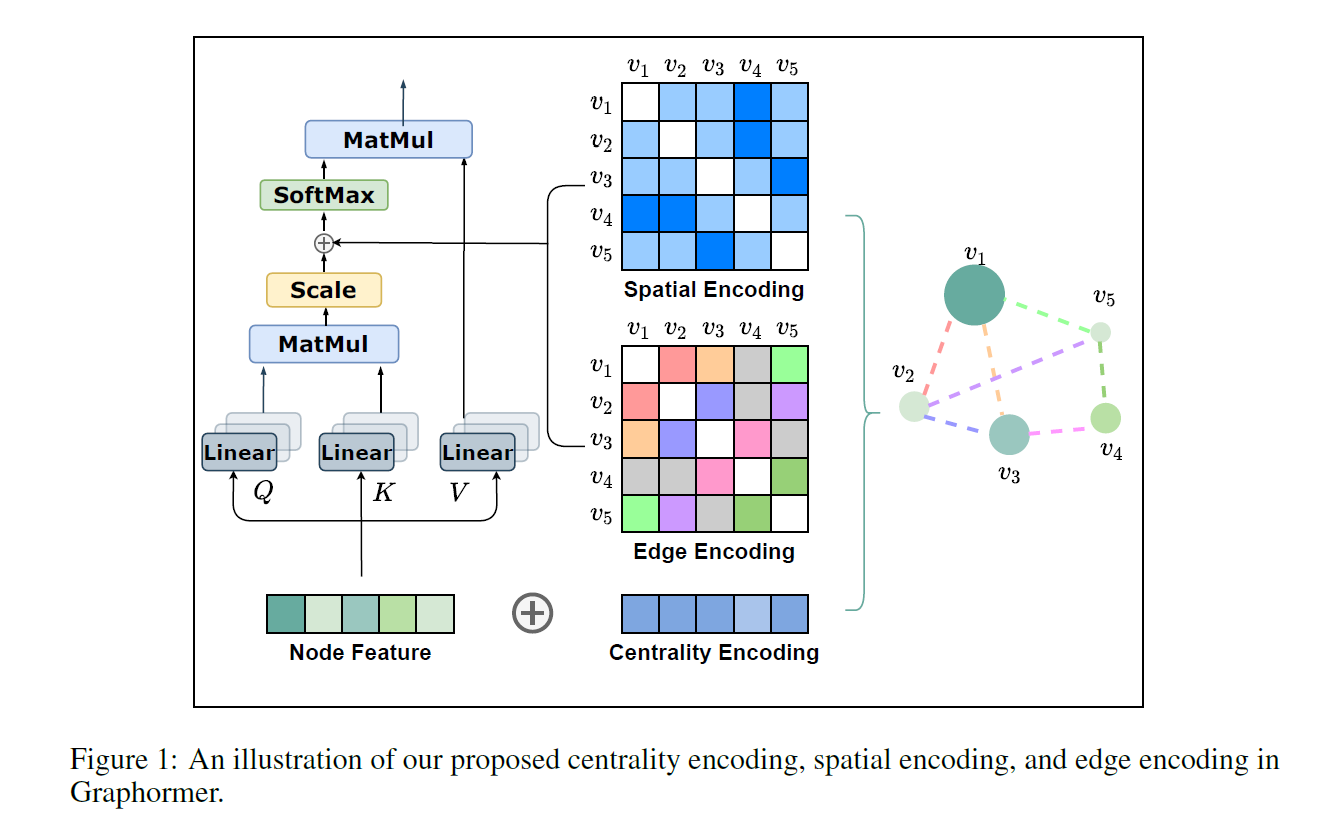
2.1. Centrality Encoding
node centrality는 한 node가 그래프에서 얼마나 중요한지를 나타내는데, 이는 그래프를 이해하는 데에 있어 사실 굉장히 중요한 정보입니다. 예를 들어 소셜 네트워크 상의 celebrity는 다른 node에 비해 훨씬 더 강한 영향력을 갖고 있을 것이고, 고객과 상점을 연결하는 그래프에서 인기 있는 상점은 다른 node에 비해 더 많은 이웃을 갖고 있을 것입니다. 이러한 정보는 현재의 attention 계산에서 적절히 활용되고 있지 못합니다.
Graphomer에서는 degree centrality를 이용했습니다. 만약 한 node가 5개의 이웃을 갖고 있다고 해보겠습니다. 그렇다면 이 node가 다른 node 하나에게 미치는 영향력은 1/5입니다. 만약 더 많은 이웃을 갖고 있다고 하면 이 영향력은 더욱 작은 크기로 계산될 것입니다. 여기서 계산된 수치가 outdegree입니다.
반대로 다른 node로 부터 받는 영향력도 존재할 것입니다. 앞서 5개의 이웃을 갖고 있다고 했습니다. 각 이웃 node들은 각각 1, 2, 2, 3, 3개의 이웃을 갖고 있다고 하면, 지금의 node는 1/1 + 1/2 + 1/2 + 1/3 + 1/3의 영향력을 수집한 셈이 됩니다. 여기서 계산된 수치가 indegree입니다.
Graphomer에서는 이러한 정보를 활요하여 Centrality Encoding을 수행합니다. 특정 node의 indegree, outdegree에 따라 2개의 임베딩 벡터를 할당하며 이들은 학습 가능한 파라미터입니다. 인코딩된 이 임베딩 벡터는 input에 자연스럽게 더해집니다.
만약 undirected 그래프라면 아래와 같은 형태가 됩니다.
\[h_i^0 = x_i + z^{-}_{deg(v_i)}\]2.2. Spatial Encoding
그래프 데이터에서 node는 연속적으로 배열되어 있지 않습니다. node는 다차원의 spatial 공간에 존재하고 edge에 의해 연결되어 있습니다. 이러한 구조적인 정보를 인코딩하기 위해서 Spatial Encoding이 필요합니다. 두 node의 spatial relation을 파악하기 위한 함수로서 본 논문에서는 최단 거리(distance of the shortest path)를 이용할 것을 제안하고 있습니다. 만약 두 node가 연결되어 있지 않다면 -1과 같은 특정 값을 부여해주면 됩니다.
결과값은 학습 가능한 스칼라이며, 이는 self-attention 모듈에서 bias 항으로 투입됩니다.
\[A_{ij} = \frac{(h_i W_Q)(h_j W_K)^T}{\sqrt{d}} + b_{\phi(v_i, v_j)}\]보통의 GNN의 경우 receptive field가 직접적인 이웃에 국한되는 경우가 많은데 이러한 구조로 인해 우리는 좀 더 범위를 확장할 수 있게 됩니다. 이는 결국 가까이 있는 node에는 더욱 attention을 두고 멀리 있다면 중요도가 낮아지는 메커니즘인 것입니다. 다만 이러한 구조를 엄청나게 큰 그래프 데이터에서 활용하기 위해서는 좀 더 고민이 필요해 보입니다.
2.3. Edge Encoding in the Attention
분자 구조 그래프에서 원자의 쌍은 어떤 연결 유형을 설명하는 feature를 갖습니다. 이처럼 그래프의 특성에 따라 edge feature가 중요한 의미를 갖는 경우가 있습니다. 기존에는 edge feature가 node feature에 더해지거나 aggregation 과정에서 함께 쓰이는 경우가 많았습니다. 그러나 이러한 방법은 전체 그래프 상에서의 edge 정보를 충분히 활용한다고 볼 수 없습니다.
논문에서는 edge feature의 인코딩 품질을 개선하기 위해 새로운 방법을 제시합니다. 각 node 쌍 $(v_i, j_j)$ 가 있다고 할 때 가장 짧은 길(shortest path) $SP_{ij} = (e1, e2, …, e_N)$ 중 하나를 찾습니다. 그리고 이 사이에 존재하는 edge feature의 내적 값의 평균과 그 path에 해당하는 학습 가능한 임베딩 벡터를 계산합니다. 이렇게 계산된 값은 2.2에서 본 것과 유사하게 attention 모듈에서 bias 항으로 투입됩니다.
\[A_{ij} = \frac{(h_i W_Q)(h_j W_K)^T}{\sqrt{d}} + b_{\phi(v_i, v_j)} + c_{ij}\] \[c_{ij} = \frac{1}{N} \Sigma_{n=1}^N x_{e_n} (w_n^E)^T\]3. How Powerful is Graphormer?
이제 생각해보아야 할 부분은 이전 chapter에서 설명한 3가지의 주요 구조가 정말로 Graphomer를 powerful하게 만들어주느냐 입니다. 결론적으로 말하면 Graphomer는 그래프 데이터에서 expressive power를 증명하기 위해 비교 대상으로 사용되는 1-Weisfeiler-Lehman Test가 구분하기 실패하는 케이스에서도 그 차이를 구분할 수 있다고 논문에서는 설명합니다. 부록 A에 이에 대한 설명이 나와있으니 참고하시길 바랍니다.
실제 구현 할 때 Graphomer Layer는 Layer Normalization과 Multi-head Attention 그리고 Feed-forward Network로 구성됩니다. 여기에 추가적으로 Special Node가 존재하는데, VNode라고 불리는 이 노드는 모든 다른 노드와 연결을 갖는 일종의 super virtual node입니다. 이 node는 왜 존재할까요?
논문에서는 이 virtual node trick으로 인해 GNN의 성능을 향상시킬 수 있다고 이야기 합니다. 개념적으로 이 virtual node는 마치 READOUT 처럼 전체 그래프의 정보를 규합하여 각 node에게 전파(propagate)하는 역할을 수행한다고 합니다. 다만 주의해야 할 것이, 단순이 이러한 virtual node를 추가하는 데에서 그쳐버리면 이는 곧 over-smoothing 문제로 이어질 수 있기 때문에 주의가 필요합니다.
4. Conclusion
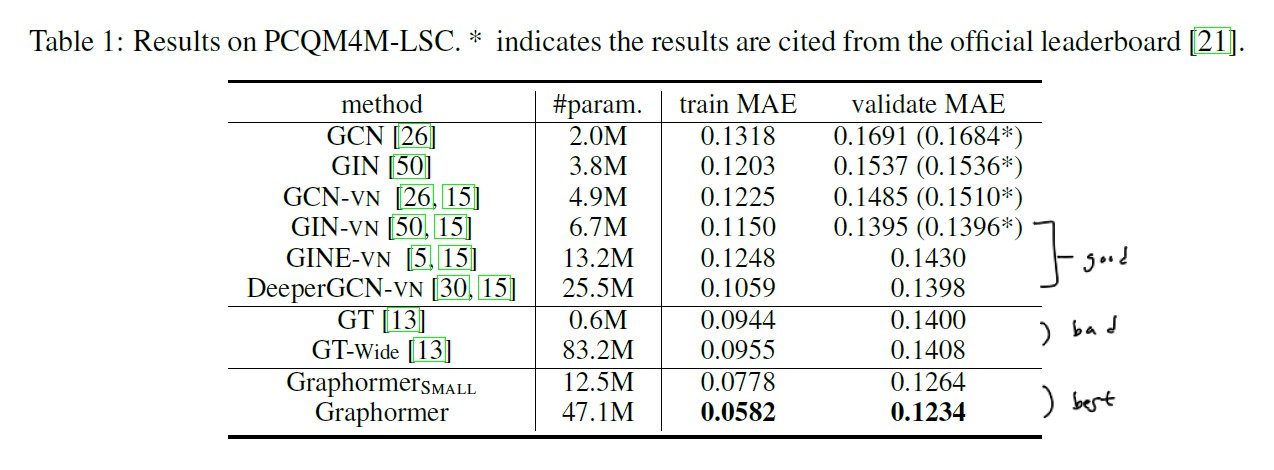
논문에서는 여러 실험에 대한 결과를 상세히 밝히고 있으며 이에 직접 논문을 참고하시길 바랍니다. 기본적으로 Graphormer는 다른 알고리즘에 비해 파라미터 수가 많고 무거운 편이나 여러 변형 버전도 존재하는 것으로 보입니다.
본 알고리즘은 흥미로운 장치와 구조를 통해 그래프 데이터에 Transformer를 더욱 효과적으로 적용할 수 있는 방법에 대해 알려주고 있습니다. 특히 Centrality Encoding의 경우 적용 범위가 상당히 넓을 것으로 보입니다. Spatial Encoding이나 Edge Encoding의 경우 현재 형태로는 엄청나게 큰 그래프 데이터에서는 직접적으로 적용하기 힘들 수는 있지만 적절한 샘플링 전략이 동반되면 좋은 효과를 발휘할 것으로 보입니다.

