BOJ 06549(히스토그램에서 가장 큰 직사각형) 문제 풀이
07 Jul 2018 | PS Stack목차
참조
| 분류 | URL |
|---|---|
| 문제 | 히스토그램에서 가장 큰 직사각형 |
| 이 글에서 설명하는 코드 | 06549_히스토그램에서 가장 큰 직사각형 |
개요
시간복잡도: $ O(TC \cdot N) $
공간복잡도: $ O(N) $
- N은 직사각형의 수, TC는 테스트 케이스의 수이다. 즉 사실상 $ O(N) $이다.
이 글에서는 히스토그램에서 가장 큰 직사각형의 가장 빠른 풀이인 스택을 활용한 풀이를 설명한다.
이 문제는 BOJ 사이트 맨 아래에 적혀 있는 대로 세그먼트 트리($O(N log N)$), 분할 정복($O(N log N)$) 등으로도 풀 수 있다.
문제 풀이
개인적으로 스택 활용 문제 중 가장 멋있는 문제라고 생각…
이 문제는 처음 봤을 때는 스택이라는 것을 떠올리기가 굉장히 까다롭다. 하지만 가장 멋있는 풀이 방법이니 꼭 익혀두도록 하자.
우선 $O(N^2)$ 풀이부터 생각해 보자.
$O(N^2)$ 풀이: 그냥 풀기
사실 이 풀이는 별 것 없다. N개의 직사각형이 있으니, [0, N) 구간이라고 생각하고, 모든 구간의 넓이를 다 구해보는 것이다. 그리고 최댓값을 찾는다.
- [0, 1) 부터 [0, 2), [0, 3), …, [0, N) 구간을 검사한다. 각 구간 최댓값을 유지하면서 차례로 검사한다.
- [1, 2) 부터 [1, 3), [1, 4), …, [1, N) 구간을 검사한다. 각 구간 최댓값을 유지하면서 차례로 검사한다.
- …
- [N-1, N) 구간을 검사한다. 각 구간 최댓값을 유지하면서 차례로 검사한다(하나뿐이지만).
- 이 중 최댓값을 찾는다.
당연히 $O(N^2)$ 풀이는 시간 초과를 얻는다. 이를 $O(N)$으로 줄이기 위해서는, 한 칸씩 검사할 때마다 $O(N)$에 해당하는 구간을 검사해야 한다.
그리고 이를 가능하게 해 주는 것이 스택이다.
$O(N)$ 풀이: 스택
이 풀이를 어떻게 생각해냈을까라는 생각은 잠시 접어두고, 우선 풀이를 보자.
- 스택을 하나 생성하고, 답(ans)은 0으로 초기화해 둔다.
- 0번째 직사각형을 처리한다. (첫 번째 직사각형이지만, 0으로 시작하는 것이 편하다)
- 0번째는 우선 스택에 집어넣어 둔다. 이 때 pair<int, int>를 사용하여, (위치, 직사각형의 높이)를 같이 저장한다.
- i번째 직사각형을 처리한다.
- 이때 스택에는 몇 개인지는 모르지만 (위치, 직사각형의 높이) 쌍이 몇 개 들어 있을 것이다.
- 스택의 top element의 높이와 i번째 직사각형의 높이를 비교한다. top element를 (top_index, top_height), i번째 직사각형을 (i_index, i_height)라고 하자.
- top_height <= i_height이면(혹은 3.iv.b에서 다 제거해버려서 스택이 비었으면) (최소 위치, 직사각형의 높이) 쌍을 스택에 집어넣고 (i+1)번째 직사각형으로 넘어간다.
- top_height == i_height이면 집어넣지 않아도 상관없지만, 코드가 복잡해지므로 그냥 한 번에 처리한다.
- 최소 높이란, min(i_height, 마지막으로 제거한 top_height)를 의미한다. 제거한 적이 없으면 그냥 i_height이다.
- top_height > i_height이면, 다음을 수행한다.
- (i_index - top_index) * top_height와 ans의 max값을 ans에 넣는다.
- top element를 제거한다. 이때 top_height는 임시저장한다.
- 모든 직사각형을 처리했으면, 남은 스택의 top element에 대해서 iv의 동작을 반복한다.
- 이때 i_index 대신 n을 사용한다.
이것이 알고리즘의 전부이다.
BOJ의 예시(2 1 4 5 1 3 3)를 적용해 보자. 아래 그림은 BOJ에서 가져온 것이다.
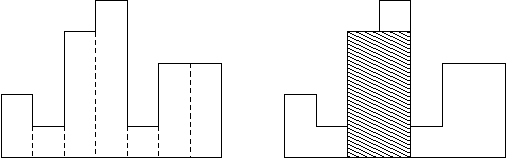
- 스택을 하나 생성하고, ans 변수는 0으로 초기화해 둔다.
- 0번째 직사각형을 처리한다.
- (0,2)를 저장한다.
- 1번째 직사각형을 처리한다.
- (0,2)가 스택에 있다.
- (0,2)와 (1,1)을 비교한다. 1번째 직사각형이 top element보다 더 작다.
- (i_index - top_index) * top_height = (1-0)*2 = 2를 ans에 저장한다.
- 이것은 0번째 직사각형만을 사용하여 잘라낸 직사각형을 의미한다. 너비 1, 높이 2짜리 직사각형이다.
- (0,2)를 스택에서 제거한다. 이때 최소 위치는 0이 된다.
- (i_index - top_index) * top_height = (1-0)*2 = 2를 ans에 저장한다.
- 스택이 비었으므로 (0,1)을 집어넣고((1,1)이 아니다!) 다음으로 넘어간다.
- 이것의 의미는 다음과 같다. 위치는 0, 높이는 1을 집어넣었다. 이는 1번째 직사각형을 포함하는(높이 1 이상) 잘라낸 직사각형의 왼쪽 끝은 0이 된다는 뜻이다.
- 그림을 보면 이해가 될 것이다. 0,1번째 직사각형 모두에서 잘라낼 때 최대 높이는 1이다.
- 2번째 직사각형을 처리한다.
- (0,1)이 스택이 있다.
- (0,1)과 (2,4)를 비교한다. 2번째 직사각형이 top element보다 더 크다.
- (2,4)를 스택에 넣고 다음으로 넘어간다.
- 3번째 직사각형을 처리한다.
- (0,1)과 (2,4)가 스택에 있다.
- (2,4)와 (3,5)를 비교한다. (3,5)를 스택에 넣고 다음으로 넘어간다.
- 4번째 직사각형을 처리한다.
- (0,1), (2,4), (3,5)가 스택에 있다.
- (3,5)와 (4,1)을 비교한다. 4번째 직사각형이 더 작다.
- (4-3)*5 = 5를 ans에 저장한다.
- 3번째 직사각형만을 사용하여 잘라낸 것을 의미한다.
- (3,5)를 스택에서 제거한다. 최소 위치를 3으로 업데이트한다.
- (4-3)*5 = 5를 ans에 저장한다.
- (2,4)와 (4,1)을 비교한다. 이번에도 4번째 직사각형이 더 작다.
- (4-2)4 = 8을 ans에 저장한다(이것이 이 예시의 정답이다*).
- 2,3번째 직사각형을 사용하여 잘라낸 것을 의미한다.
- (2,4)를 스택에서 제거한다. 최소 위치를 2로 업데이트한다.
- (4-2)4 = 8을 ans에 저장한다(이것이 이 예시의 정답이다*).
- (0,1)과 (4,1)을 비교한다. 높이가 같으므로 (2,1)((4,1)이 아니다!)을 스택에 집어넣고(넣지 않아도 된다) 다음으로 넘어간다.
- 5번째 직사각형을 처리한다.
- (0,1), (2,1)이 스택에 있다.
- (5,3)은 (2,1)보다 높이가 높기 때문에 스택에 그대로 집어넣고 다음으로 넘어간다.
- 6번째 직사각형을 처리한다.
- (0,1), (2,1), (5,3)이 스택에 있다.
- (6,3)은 (5,3)과 높이가 같기 때문에 스택에 그대로 집어넣고 다음으로 넘어간다.
- 이제 모든 직사각형을 처리했으니, 스택을 비워가면서 처리를 하면 된다.
- (0,1), (2,1), (5,3), (6,3)이 스택에 있다.
- (6,3): (7-6)*3 = 3은 ans보다 작다. 6번째 직사각형만을 사용하여 잘라낸 것(너비 1, 높이 3)이다.
- (5,3): (7-5)*3 = 6은 ans보다 작다. 5,6번째 직사각형을 사용하여 잘라낸 것(너비 2, 높이 3)이다.
- (2,1): (7-2)*1 = 5은 ans보다 작다. 4,5,6번째 직사각형을 사용하여 잘라낸 것(너비 5, 높이 1)이다.
- (0,1): (7-0)*1 = 7은 ans보다 작다. 0~6번째 직사각형을 모두 사용하여 잘라낸 것(너비 7, 높이 1)이다.
같은 방법으로
1,2,3,2,1(정답은 1~3번째 직사각형을 사용한 6)과
3,2,1,2,3(정답은 0~4번째 직사각형을 모두 사용한 5)
에 대해서도 생각해 보라.
이 알고리즘에 왜 동작하는지를 살펴보면 다음과 같다.
- 스택에는 항상 위치와 직사각형의 높이 모두 오름차순으로 정렬되어 쌓여 있다. top element가 더 높으면 항상 제거하기 때문에 이렇게 된다.
- i번째 직사각형을 처리할 때, 1에 의해 놓치는
잘라낸 직사각형이 없게 된다.- 즉, (i-1)번째 직사각형이 잘라낸 직사각형의 오른쪽 끝이 되는 모든 경우를 처리하는 것이다.
- 최소 높이를 사용하는 이유는, 3,2,1,2,3과 같은 경우를 처리하기 위함이다.
- 만약에 3번째 직사각형을 처리할 때 (2,1)로 그대로 집어넣어 버리면, 0~4번째 직사각형을 모두 포함한 넓이 5짜리 직사각형을 놓치게 된다.
- 1에 의해 i번째 직사각형보다 낮은 top element를 처음 만나기 전까지는 모두 top element가 i번째 직사각형보다 높으므로, 높이 걱정을 할 필요가 없어진다.
이해가 안 된다면, 예시를 몇 개 더 생각해 보면서 해야 한다. 추천하는 예시는 1,2,5,2,2,1,6이다.
다음은 자주 하는 실수를 정리한 것이다.
- 마지막에 스택을 비우는 작업을 안 하는 경우. 이것은 마지막 직사각형이 잘라낸 직사각형의 오른쪽 끝이 되는 경우를 놓친 것이다.
- 높이 10억 * 너비 10만은 int의 범위를 한참 넘는다. ans는 long long으로 선언할 것.
구현
이 문제에 적용 가능한 트릭이 몇 가지 있다.
- 높이가 같은 경우 스택에 넣어도 되고 안 넣어도 된다. 직관을 위해서라면 넣지 말고, 코딩의 편의성을 위해서라면 따로 처리할 필요 없다.
- 스택을 비우는 작업을 따로 처리하는 대신, 높이 -1짜리 가상의 n번째 직사각형을 생각하자. 그러면 모든 직사각형은 이 n번째 직사각형보다 높기 때문에 스택에서 모두 제거되게 된다.
최소 위치는 left이다.
설명이 복잡한 것 치고는 간결한 코드이지 않은가?
#include "../library/sharifa_header.h"
int main_06549() {
int n;
while (true) {
scanf("%d", &n);
if (!n)break;
stack<pair<int,int> > st;
ll ans = 0;
for (int i_index = 0; i_index <= n; i_index++) {
int i_height;
if (i_index < n)
scanf("%d", &i_height);
else
i_height = -1;
int left = i_index;
// top_index: st.top().first, top_height: st.top().second
while (!st.empty() && st.top().second > i_height) {
ans = max(ans, ((ll)i_index - st.top().first)*st.top().second);
left = st.top().first;
st.pop();
}
st.push(make_pair(left, i_height));
}
printf("%lld\n", ans);
}
return 0;
}
주의: 이 코드를 그대로 복붙하여 채점 사이트에 제출하면 당연히 틀린다. 못 믿겠다면, 저런 헤더 파일이 채점 사이트에 있을 것이라 생각하는가?

