Gorio Tech Blog search

GitHub 사용법 - 02. 프로젝트와 repository 생성

29 Jun 2018 | GitHub usage

주의: 이 글을 읽는 여러분이, 만약 git을 많이 써 봐서 익숙한 것이 아니라면, 반드시 손으로 직접 따라 칠 것을 권한다. 눈으로만 보면 100% 잊어버린다.

Remote Repository 생성

우선 https://github.com/에 접속하여 로그인한다(회원가입은 되어 있어야 한다). 그러면 다음과 비슷한 화면이 보인다.

01_new_repository

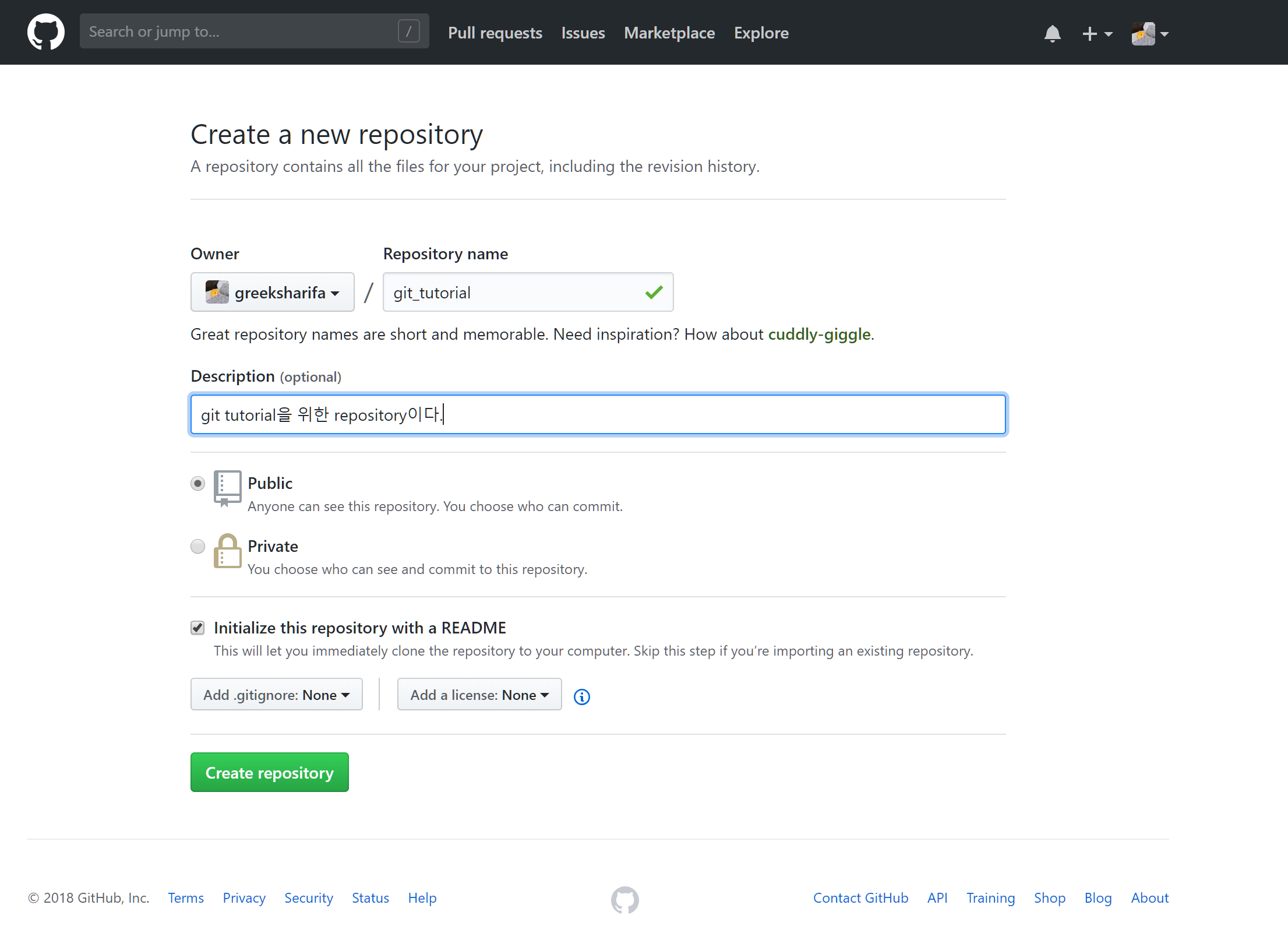
New repository를 클릭한 후, 프로젝트 이름을 git_tutorial으로 입력한다. 원하는 이름으로 해도 상관없다.
또 Description을 성심성의껏 잘 작성한다.

그리고 Initialize this repository with a README 체크박스에 체크한다.
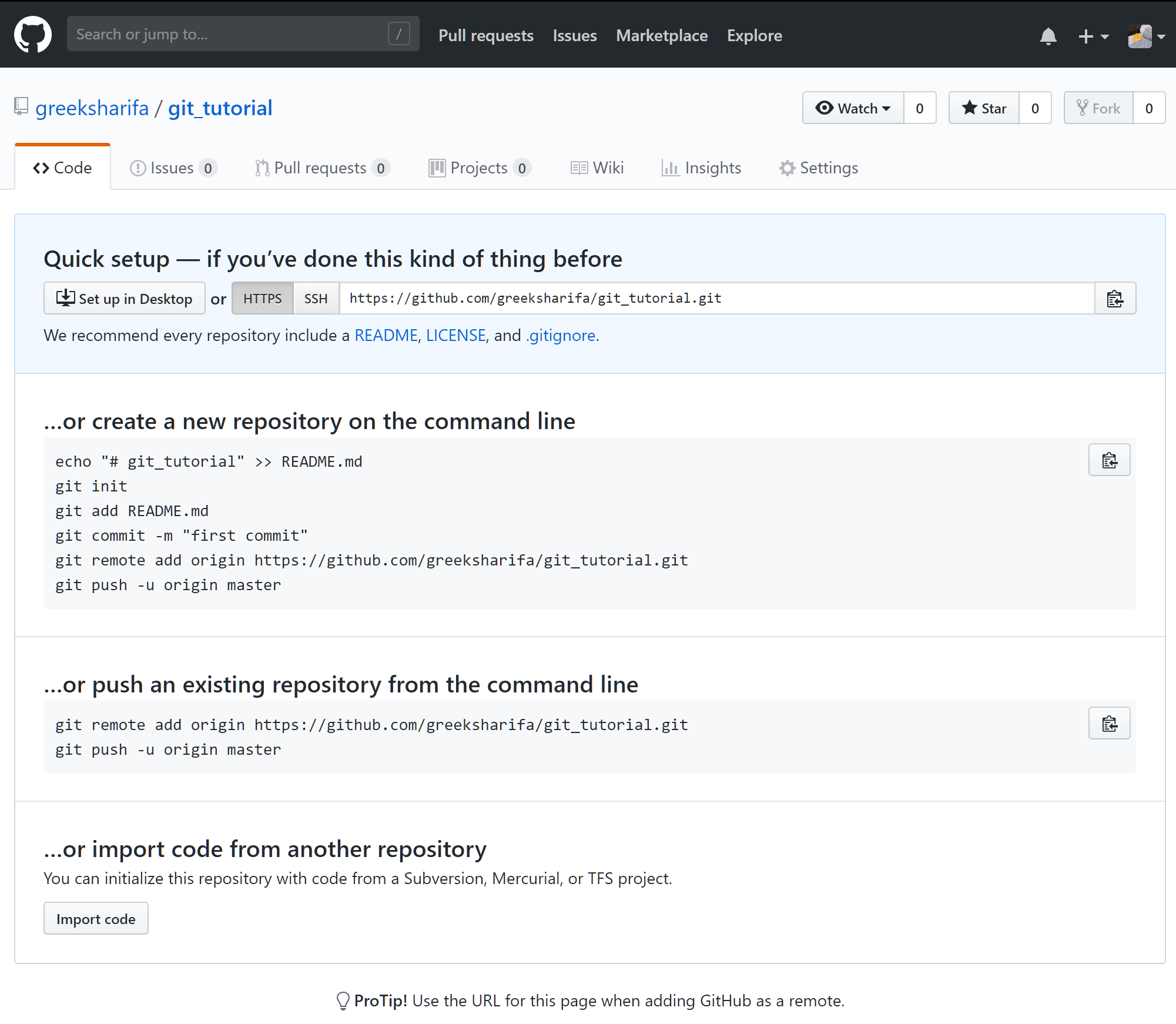
체크하지 않고 만든다면 git repository를 처음 만든 이후 local repository와 연결하는 방법을 알려주는 안내 글이 뜬다. 이를 읽어 봐도 괜찮다.

지금은 체크하지 않는 것이 간단하므로 체크하지 않겠다. 그림에 체크되어 있는 것은 무시하자.

02_create_a_new_repository

마지막으로 Create repository를 누른다.

그러면 이제 여러분의 GitHub 계정에 git_tutorial이란 이름의 remote repository가 생성될 것이다.

02_create_a_new_repository

Local Repository 생성

그리고 이제 local에서 directory를 하나 생성한다. Directory 이름은 프로젝트와 같은 이름으로 하고, 생성하는 위치는 본인 마음대로 하면 된다.

02_create_a_new_repository

다음으로 명령창(터미널 또는 cmd 창)을 하나 띄운다. cd '경로명'/git_tutorial으로 하면 된다. 예시는 절대 경로이지만, 상대 경로로 해도 무방하다.
필자는 윈도우 환경(cmd)에서 진행하였다.

cd C:\Users\Sharifa-D\WebstormProjects\git_tutorial

그리고 다음 명령들을 수행해 본다. 만약에 git이 유효한 명령이 아니라는 error가 뜬다면, 본인의 운영체제이 맞는 git을 설치해야 한다.
윈도우의 경우 여기에서 다운받아 설치하면 된다(64bit 기준).

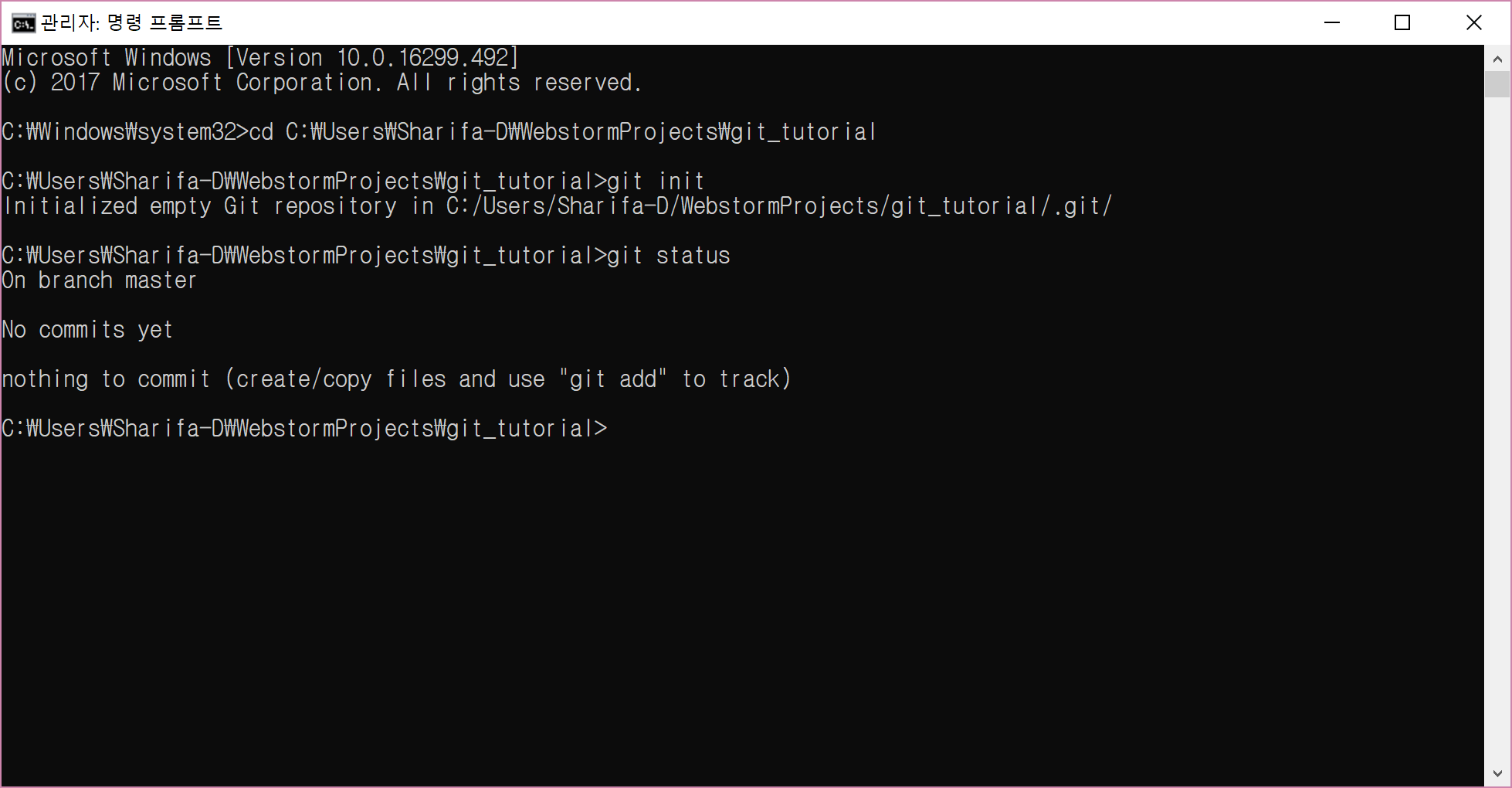
git init
git status

똑같은 과정을 거쳤다면, 다음 그림과 같은 화면이 나올 것이다.

02_create_a_new_repository

여기까지 했다면, local repository를 성공적으로 생성한 것이다. 오류가 뜬다면, 복잡해 보이는 에러 메시지를 그대로 복붙하여 구글링하면 된다.
여러분이 겪는 문제는 다른 사람들도 겪어 본 문제라는 것을 해결법과 함께 알 수 있다.

프로젝트 수정

파일 생성하고 수정하기

이제 여러분은 1) remote repository와 2) local repository를 모두 생성했다. 그러면 이제 두 repo(repository)를 연결하는 부분이 필요할 것이다.

연결은 어렵지 않다. 하지만 그 전에 파일을 조금 작성해보자. 빈 프로젝트 갖고 뭘 하기엔 심심하지 않은가?

first.py란 파일을 하나 생성한다. 그리고 다음과 같은 내용을 작성해보자.

print("Hello, git!") # instead of "Hello, World!"

심심하다면 python first.py를 명령창에 입력해 보자.

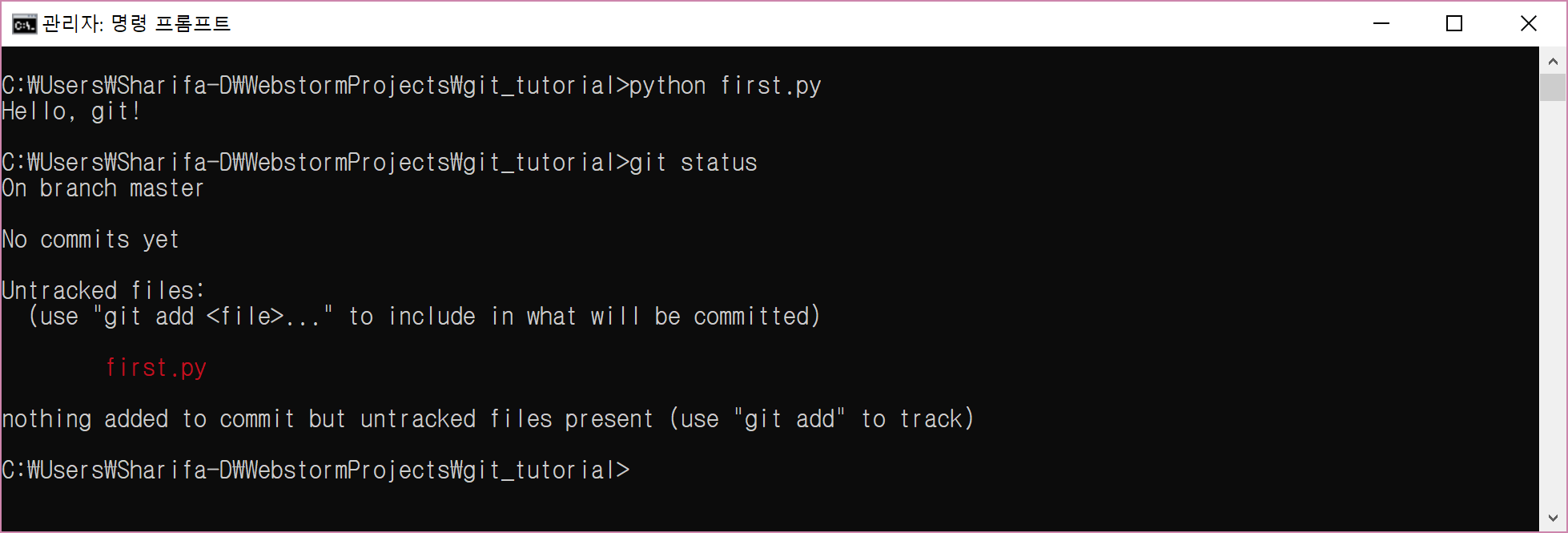
그리고 git status를 다시 입력한다. 조금 전과는 다른 화면을 볼 수 있다.

02_create_a_new_repository

여기서 중요한 정보를 몇 개 찾을 수 있다. 앞으로 git을 사용할 때에는 무슨 메시지가 뜨는지 (전부) 살펴보는 것이 굉장히 중요하다. 뭔가 잘못되었는지 아닌지를 볼 수 있기 때문이다.

위에서부터 하나씩 살펴보면 아래와 같다.

  • On branch master
    • 지금 작업하는 branch가 master라는 의미이다. 본인이 어떤 branch에서 작업 중인지 확인하는 습관을 반드시 가지도록 한다. branch를 잘못 옮긴 줄 모르고 작업을 이어갔다가는 큰일 날 수 있다.
  • No commits yet
    • 아직 생성한 commit이 없다는 뜻이다. 이후에 commit을 추가하면, 이 부분이 다르게 보일 것이다.
  • Untracked files: (use “git add ..." to include in what will be committed)
    • 여러분이 수정하긴 했지만 staging area에 올라가지 않은 파일의 목록이다. staging area에 올라갔다는 말은 track한다는 말과 같다.
  • first.py
    • 여러분은 아직 git add 명령을 사용하지 않았기 때문에 수정/생성/삭제한 유일한 파일인 first.py가 tracking되지 않고 있다.
  • nothing added to commit but untracked files present (use “git add” to track)
    • tracking하려면 git add를 쓰라고 한다. 메시지에는 도움이 되는 내용이 많다.

조금 더 자세히 설명하기 위해, second.py 파일을 생성한다.

print("Why don't you answer me, git?")

git add

그리고 조금 전 메시지가 친절히 알려줬던 git add 명령을 사용하려고 한다. 명령창에 다음과 같이 입력한다.

git add first.py

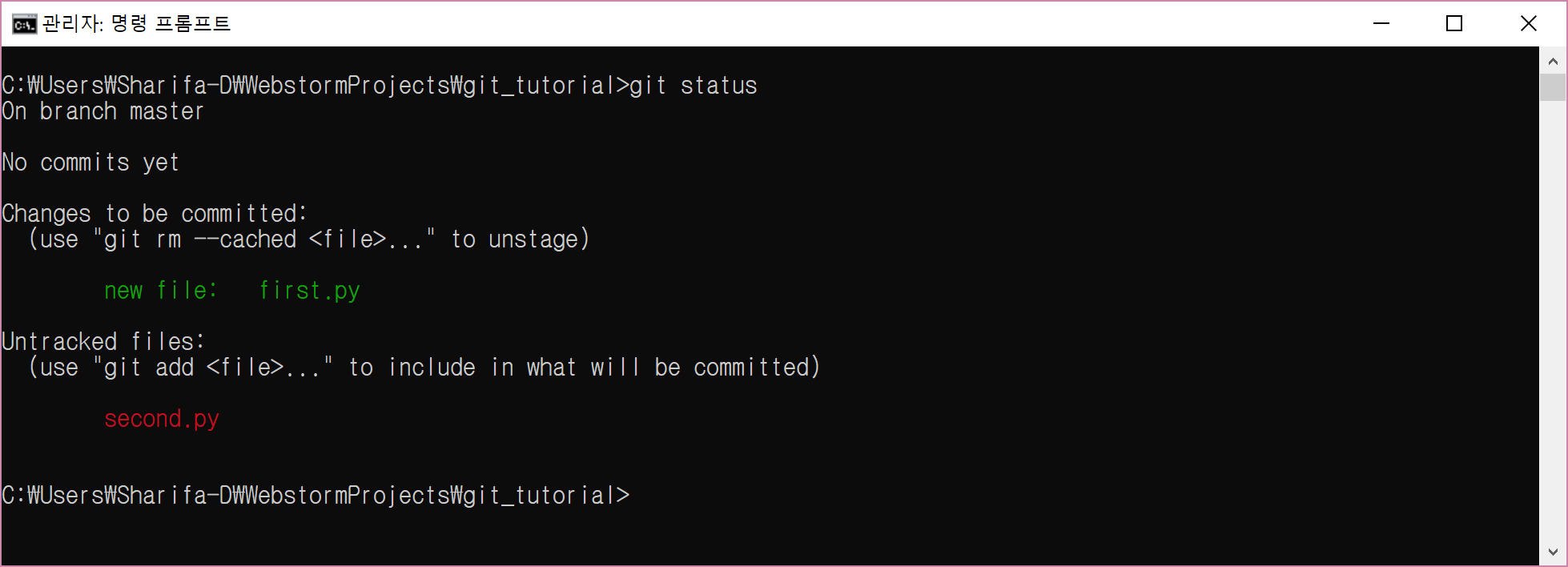
이제 다시 한번 git status를 입력하면, 아까보다 메시지가 더 많은 것을 확인할 수 있다.

02_create_a_new_repository

그림을 보면 tracking되고 있는 파일은 초록색, untracked file은 빨간색으로 되어 있음을 알 수 있다. 여러분은 first.py 는 git add로 추가했기 때문에 초록색으로, second.py는 그러지 않았기 때문에 빨간색으로 남아 있음을 확인할 수 있다.

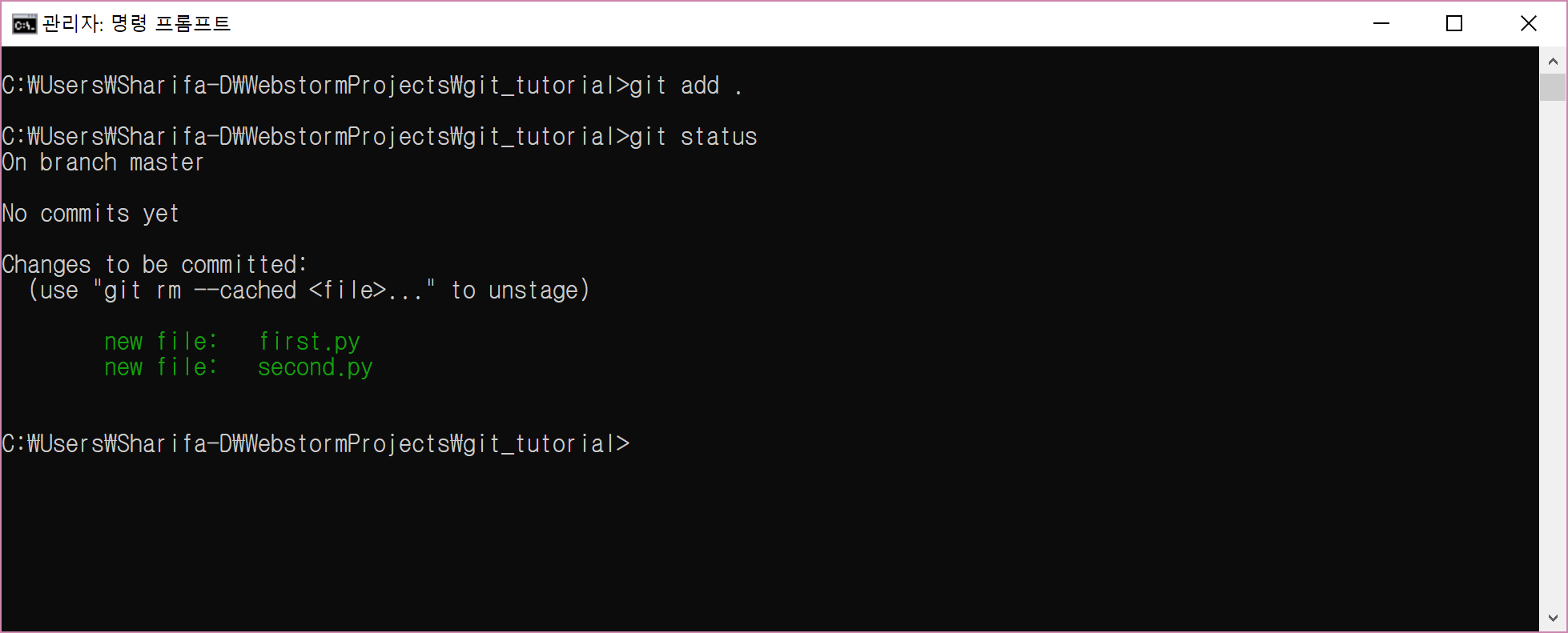
이번에는 다른 명령을 연습해보자. git add .을 입력한다. git status로 확인해보면?

02_create_a_new_repository

.의 의미는 모든 파일과 디렉토리이다. 즉, 여러분은 프로젝트에 존재하는 모든 파일(first.py와 second.py)를 staging area에 추가한 것이다.

옵션으로, git add의 다양한 버전을 표로 정리해 두었다.

명령어 Description
git add first.py first.py 파일 하나를 staging area에 추가한다.
git add my_directory/                               my_directory라는 이름의 디렉토리와 그 디렉토리 안의 모든 파일과 디렉토리를 staging area에 추가한다.
git add . 현재 폴더의 모든 파일과 디렉토리, 하위 디렉토리에 든 전부를 staging area에 추가한다. 규모가 큰 프로젝트라면 써서는 안 된다.
git add -p [<파일>] 파일의 일부를 staging하기
git add -i Git 대화 모드를 사용하여 파일 추가하기
git add -u [<경로>] 수정되고 추적되는 파일의 변경 사항 staging하기

옵션: 같은 파일이 changes to be committed와 Untracked files 모두에 있는 경우

이 부분은 옵션이다. git이 아직 잘 이해가 되지 않는다면, 반드시 할 필요는 없다. 여기로 바로 넘어가면 된다.

first.py 파일을 다음과 같이 수정한다.

print("Hello, git!") # instead of "Hello, World!"
print("Don't you hear me, git?")

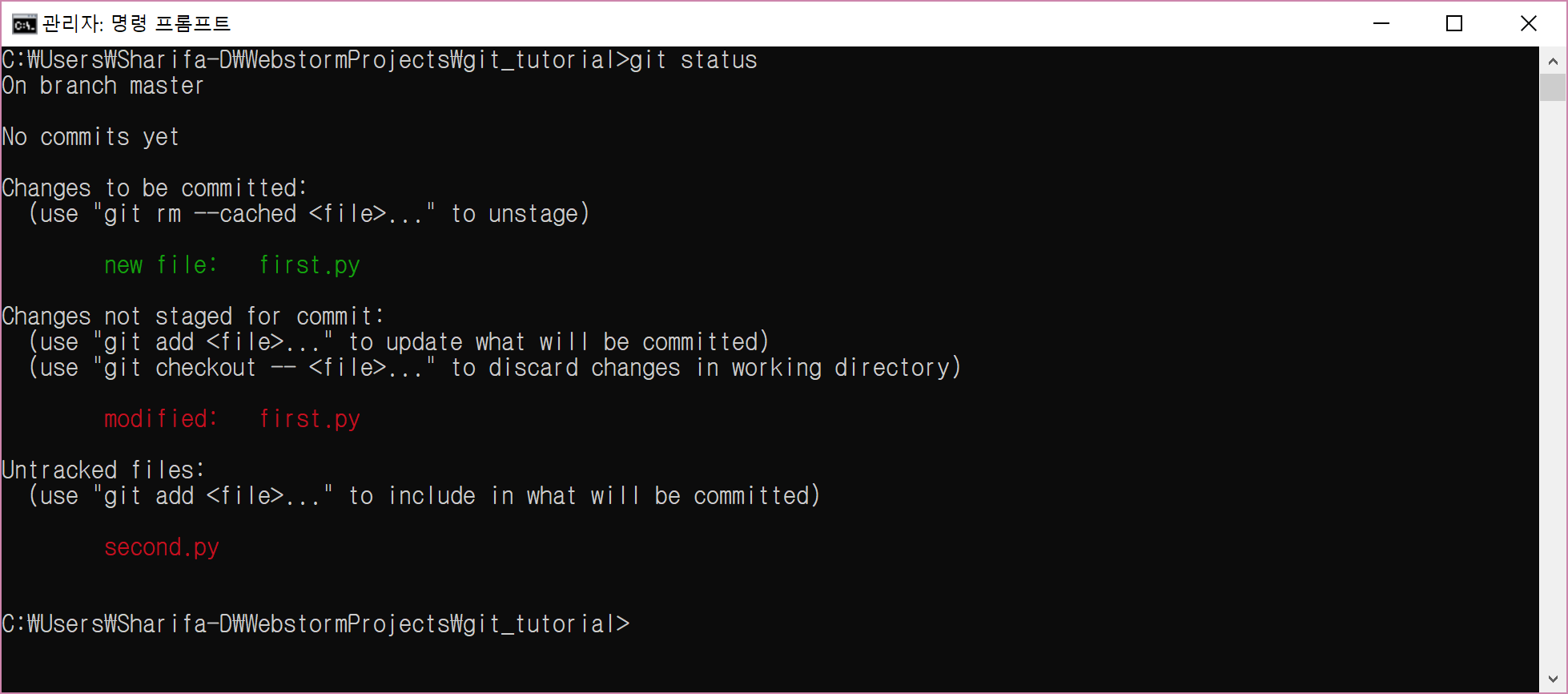
그리고 다른 명령을 하지 않은 채로 git status를 명령창에 입력한다. 그럼 다음과 같을 것이다.

02_create_a_new_repository

여러분이 한 것을 되짚어 보면 다음과 같다.

  1. first.py를 생성 및 수정하였다.
  2. first.py를 git add 명령으로 staging area에 추가하였다.
  3. first.py를 또 수정하였다.
  4. 다른 명령(git add나 git commit 등)을 하지 않는 채로 git status로 상태를 확인하였다.

이런 과정을 거쳤을 때 여러분은 동일한 파일이 changes to be committed와 Untracked files에 모두 있는 광경을 볼 수 있는 것이다.

즉, 이는 오류가 아니라,

  • 이미 git add로 추가한 적이 있으니 changes to be committed에 있는 것이고
  • 그 이후에 수정한 사항은 staging area에 올라가지 않았으니 Untracked files에도 있는 것이다.

어렵지 않게 이해할 수 있을 것이다.

옵션: git add 취소, git rm –cached <file>

여러분이 메시지를 꼼꼼히 읽어봤다면, 다음과 같은 문구를 보았을 것이다.

(use “git rm –cached ..." to unstage)

이는 staging area에 올라간 파일을 unstage하겠다는 뜻으로, git add를 취소하는 것과 같은 효과를 가진다. 즉 cached된 <file>을 (staging area에서) rm(remove)하겠다는 의미이다.

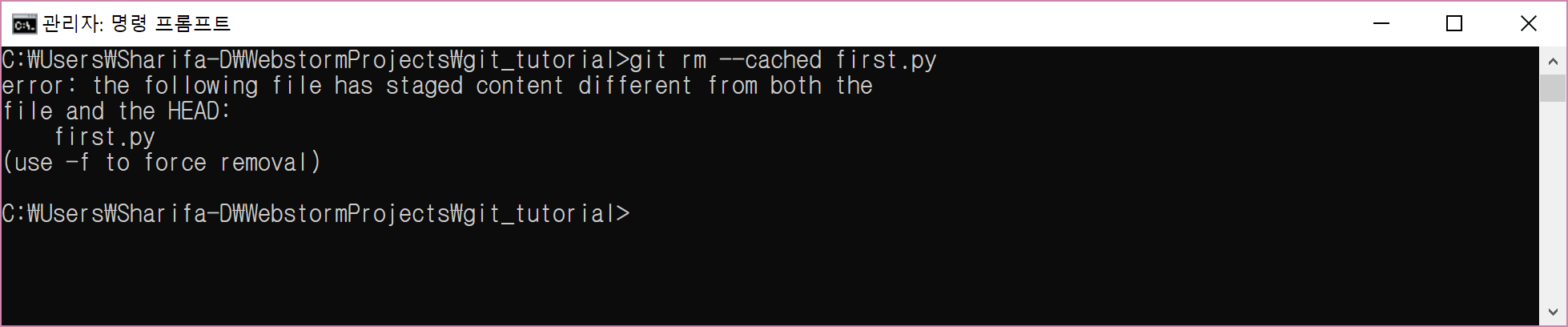
무슨 일을 하는지 알았으니, git rm --cached first.py를 명령창에 입력한다. 그리고 git status를 쳐보자.

02_create_a_new_repository

에러가 뜬다. 메시지를 의역하면, first.py가 실제 파일 내용이랑 git이 인식하는 파일 내용이 달라서 staging area에서 제거할 수 없다는 뜻이다.

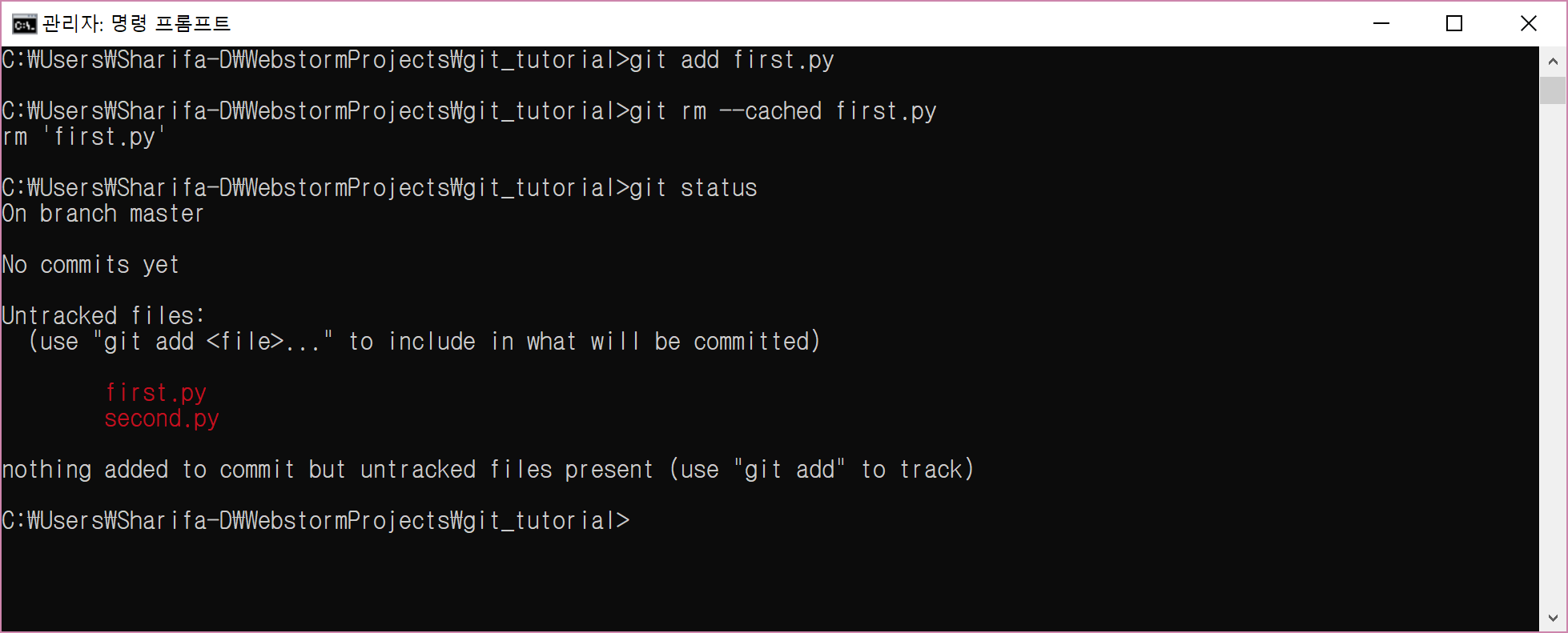
어차피 여러분은 이 파일을 unstage하는 것이 목적이었으므로, git add first.py이후 git rm --cached first.py를 입력해주면 그만이다. git status로 상태를 확인해주자.

02_create_a_new_repository

이제 옵션을 안 한 상태로 되돌리기 위해, first.py에 추가한 내용을 지우고 git add .를 입력한다.

git commit

현재 다음과 같은 상태일 것이다.

02_create_a_new_repository

이제 commit을 할 차례이다. 커밋이란 수정사항들을 하나로 묶는 것이라 보면 된다.
실제 프로젝트에서 하나의 커밋이란 하나의 기능이라 보면 된다. 하니의 기능이란 새 기능일 수도 있고, 버그 수정일 수도 있고, 단순 개선 사항일 수 있다.

커밋은 여러 종류가 있지만, 가장 간단한 버전은 다음과 같다.
주의: 아직 명령창에 적지 않는다.

git commit -m “commit-message”

명령어를 입력할 때 -에 알파벳을 붙여 쓰는 경우가 있다. 이는 옵션을 주겠다는 의미이다.
-m 옵션을 주면서 "로 묶은 메시지를 전달하면, commit-message라는 description으로 커밋을 하나 만든다라는 의미가 된다.

옵션: 좋은 commit message 작성법

왜 명령창에 적지 말라고 했냐면, 이 방식으로 하는 것은 큰 프로젝트를 다룰 때 굉장히 안 좋은 습관이다. 고작 한 문장짜리로 커밋의 모든 내용을 설명할 수 있겠는가? 만약에 커밋 내용이 다음과 같은 일을 한다고 하자.

이 커밋은 #101번과 #104번 이슈를 해결하기 위해 작성된 것이다. 이 문제에 관한 자세한 내용은 #203번과 #223번을 참조하라.
해당 문제를 해결하기 위해 다음과 같은 방법을 사용하였다. 블라블라
문제는 해결되었지만, 아직 다음과 같은 (사소한) 문제가 남아 있다. #401번을 참조하라.

한 문장에 실수 없이 적을 수 있겠는가?
자신이 있다면 말리진 않겠지만, 별로 좋은 습관이 아니란 것은 명확하다.

좋은 commit message 작성법에 관한 내용은 여기를 참조하라.

다시 commit하기

아무튼 다음과 같이 입력한다.

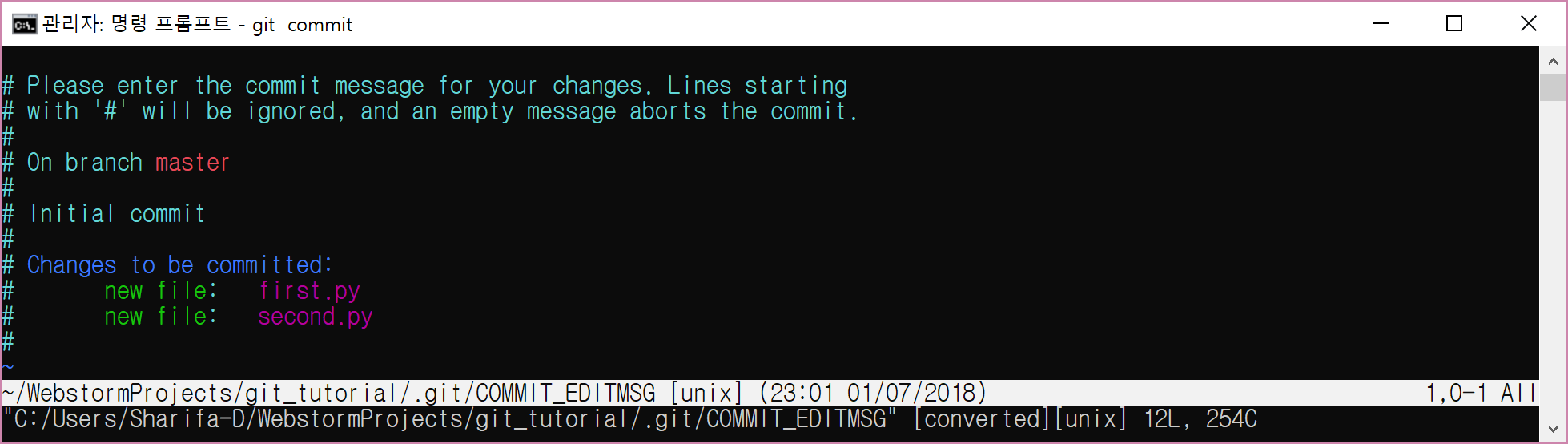
git commit

그럼 뭔가 화려한 편집 창이 보인다. vi 편집기라고 보면 된다.

02_create_a_new_repository

i를 누른다. insert를 한다는 뜻이다.
그리고 commit message를 최대한 상세히 입력한다.

다 입력했으면, ESC를 누른다. 그리고, :wq를 입력한 후 Enter를 누른다.

02_create_a_new_repository

vi 편집기에서는, 입력 모드와 명령 모드가 있다.
입력 모드는 일반적인 텍스트 편집기와 같다.
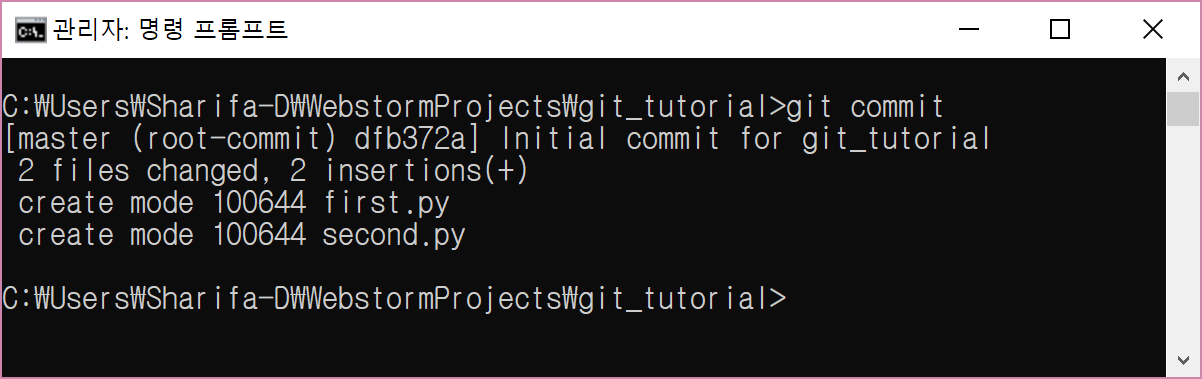
명령 모드는 옵션을 주고 여러 조작을 할 수 있다. 자세한 설명은 Vim 사용법를 참조하면 된다. 여기서는 w는 저장이고 q는 quit을 의미한다는 것만 알아도 된다.

이제 commit에 대한 간단한 설명이 끝났다.

Remote & Local Repository 연결

이제 연결을 할 차례이다. 근데 할 것이 한 가지 더 남았다. 사용자 등록 과정이다.

등록 과정은 두 가지 방법이 있다. 전역 설정을 하느냐, repo 별로 설정을 하느냐이다.

  • 전역 설정
    • git config --global user.name "Your name"
      • 여러분의 github 아이디를 적으면 된다.
    • git config --global user.email "Your email"
      • 여러분의 github 이메일 계정을 적으면 된다.
  • repo별 설정
    • git config user.name "Your name"
      • –global 옵션이 없다. 여러분의 github 아이디를 적으면 된다.
    • git config user.email "Your email"
      • 역시 –global 옵션이 없다. 여러분의 github 이메일 계정을 적으면 된다.

전역 설정과 repo별 설정의 차이를 굳이 설명할 필요는 없을 것이다.

일단은 global 설정부터 시작하자. Your name/email은 여러분 스스로 입력하길 바란다.

git config –global user.name “Your name” git config –global user.email “Your email”

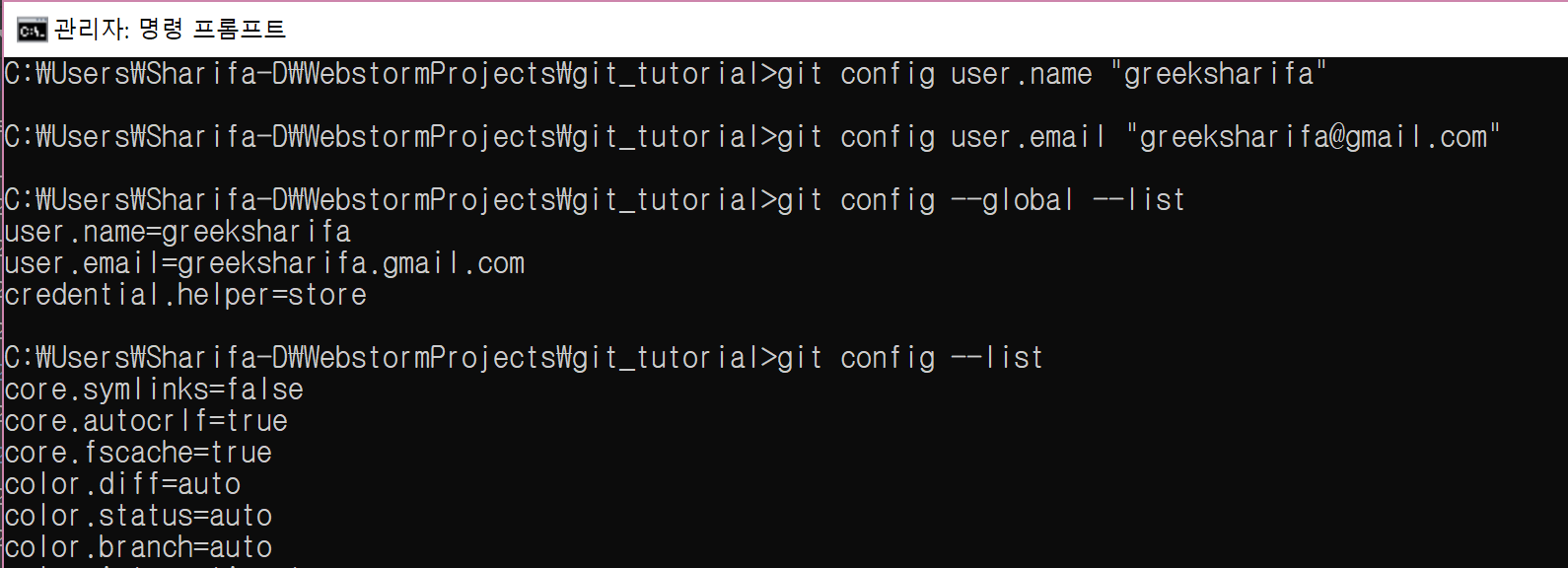
추가로 해야만 하는 것은 없지만, 등록된 사용자를 확인하는 방법도 알아야 하지 않겠는가?

명령어 Description
git config –global –list 전역 설정 정보 조회
git config –list repo별 설정 정보 조회

02_create_a_new_repository

이제 진짜로 연결하는 과정이다. 딱 한 문장으로 끝난다.

git remote add <remote repo 이름> <repo url>
ex) git remote add origin https://github.com/greeksharifa/git_tutorial.git

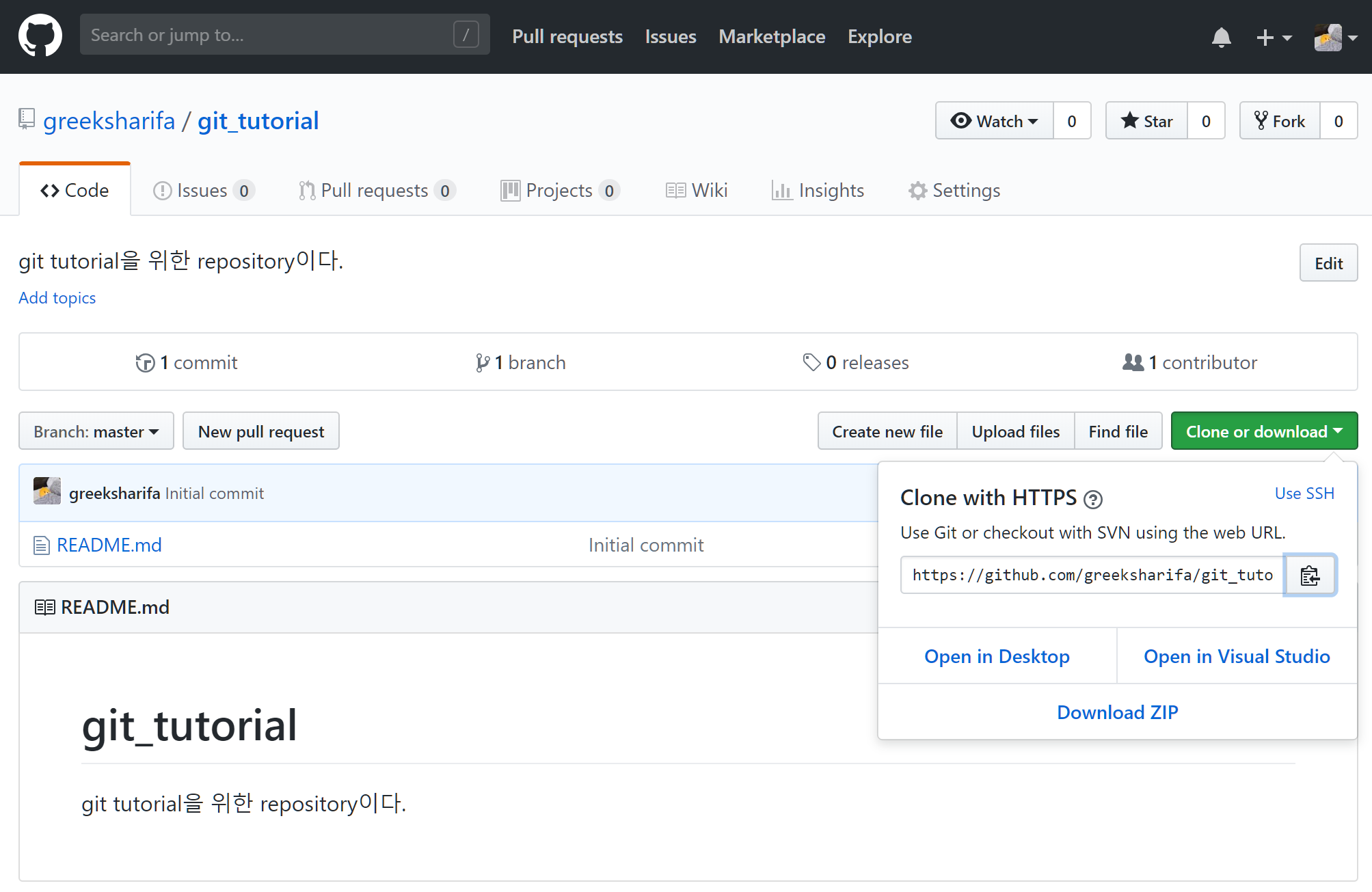
url은 여기서 확인할 수 있다.

02_create_a_new_repository

일반적으로 remote repo의 이름은 origin으로 둔다.

옵션: git 설정하기

다음 명령은 Git의 출력결과 색상을 활성화하는 명령이다.

git config --global color.ui “auto”

앞으로 git push를 할 때마다 git 비밀번호를 입력해야 하는데, 이것이 매우 귀찮다면 비밀번호를 저장해 둘 수 있다.

git config --global credential.helper store

단 보안상의 이슈가 걱정된다면, store 대신 cache 옵션을 주어 15분간 저장되게 할 수 있다. 15분 대신 다른 시간을 지정하려면 다음과 갈이 한다.

git config --global credential.helper cache –timeout 86400

git pull, git push

이제 정말로 연결한 remote repo에 local repo의 수정사항을 올릴 때가 되었다. push 명령은 어렵지 않다.

git push origin master

한동안 origin이라는 이름만 쓰고 master branch만 이용할 계획이라면, 위의 명령에 -u 옵션을 붙인다. 즉, git push -u origin master라고 입력하면 된다.
그러면 앞으로 git push만 입력해도 origin master에 push가 이루어진다.

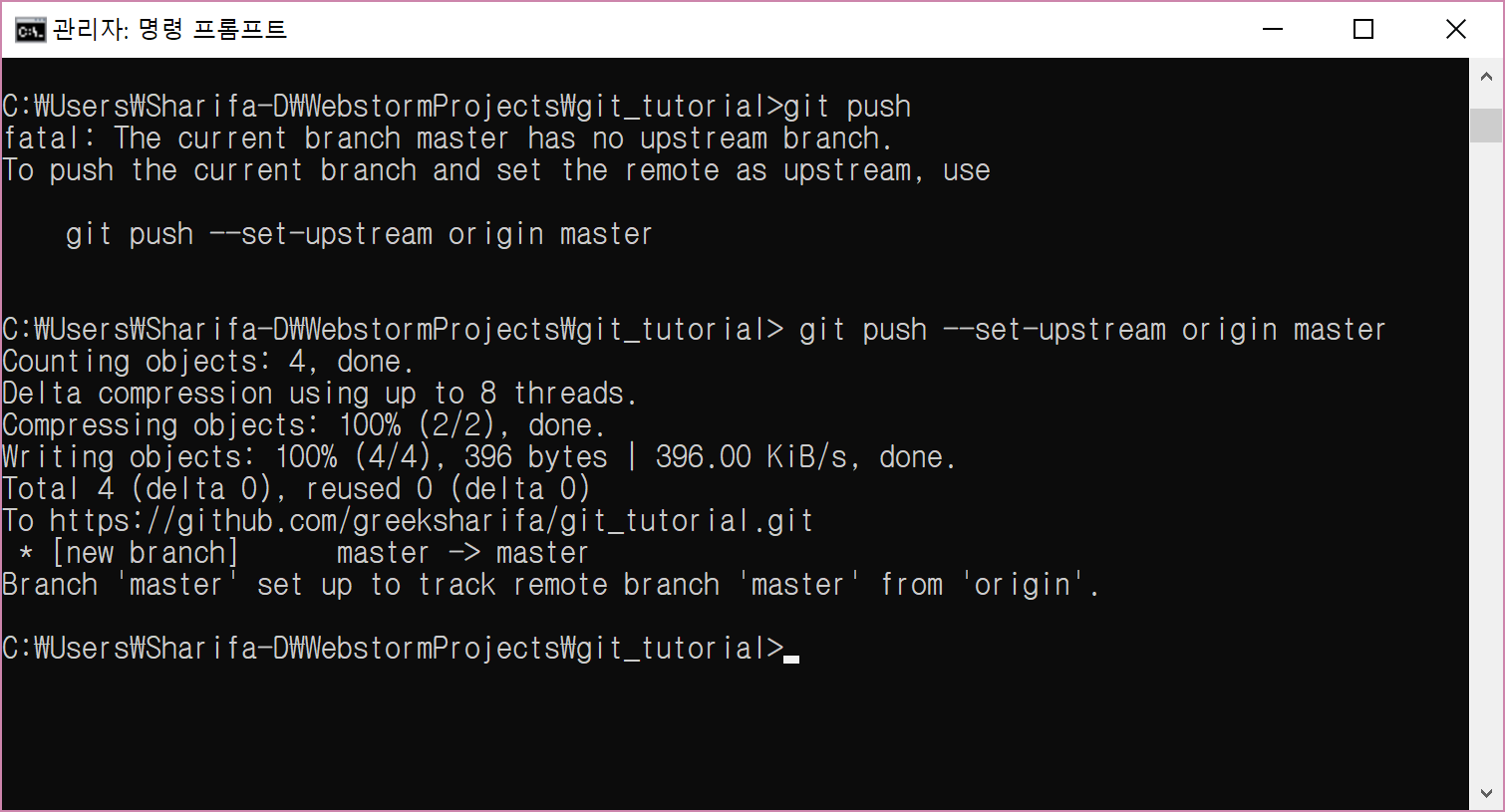
그런데 이때 그냥 push를 하면 error가 뜰 수 있다. 이는 remote repo를 만들 때 README.md 파일을 생성했기 때문이다.
GitHub Instruction에서 간략히 설명한 대로, git pull origin master(혹은 그냥 git pull)으로 remote repo의 변경사항을 local repo로 받아온다.

그리고 현재의 master branch와 remote repo의 branch를 연결하기 위해, 다음과 같이 입력한다.
여기서 upstream branch란 remote repo의 branch를 가리키는 말이라 봐도 좋다.

git push –set-upstream origin master

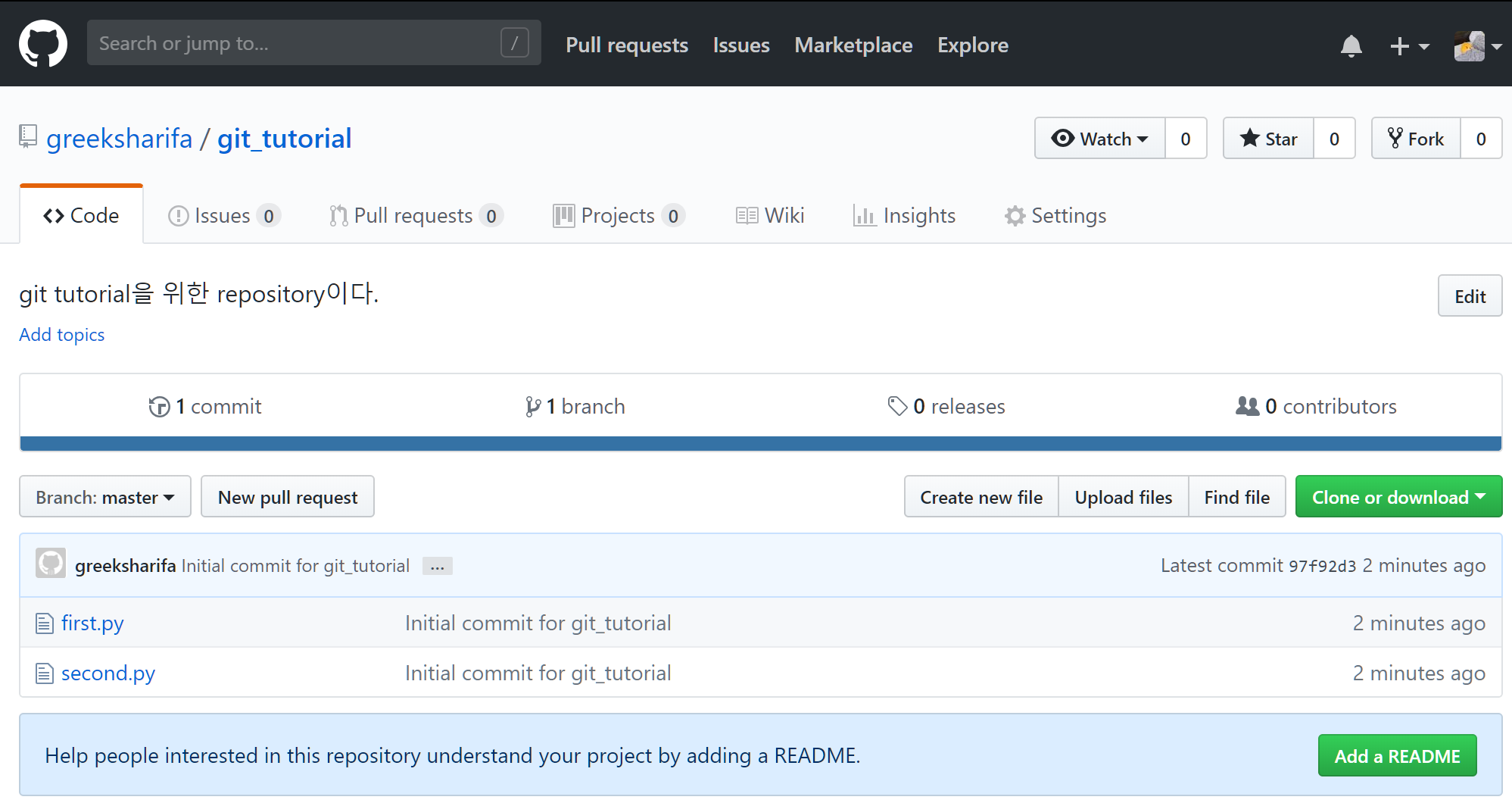
02_create_a_new_repository

이제 브라우저에서 git_tutorial repo를 확인해 본다.

02_create_a_new_repository

끝났다!

다음 글에서는 프로젝트 clone, status, .gitignore에 대해서 알아본다.

Git 명령어

GitHub 사용법 - 00. Command List에서 원하는 명령어를 찾아 볼 수 있다.

Comment  Read more

GitHub 사용법 - 01. 소개

29 Jun 2018 | GitHub usage

Git이란?

Git은 버전 관리 시스템으로, 파일의 변경 내용을 계속 추적하도록 개발된 것이다. 즉 Git은 분산 버전 관리 시스템으로, 모든 사람이 프로젝트의 현재와 과거 모두의 전체 history를 갖고 있는 것이다.

GitHub이란?

GitHub은 Git repository를 업로드하는 웹사이트이다. 여러분이 알고 있는 그 깃헙 맞다.

Git을 사용하는 이유까지 설명하지는 않도록 하겠다.

Git에서 사용되는 개념

Repository 저장소

저장소는 당연히, 프로젝트 파일을 모아둔 곳이다. 하나의 root directory와 비슷한 개념이다.

저장소에는 크게 세 가지 종류가 있다고 생각해도 무방하다. 이 중 두 개는 거의 비슷한데, 소유자가 다를 뿐이다.

  1. 나의 remote repository
  2. 다른 사람의 remote repository
  3. 나의 local repository

4. 다른 사람의 local repository

물론 4번은 여러분이 신경쓸 부분은 아니다. 따라서 세 가지만 생각하면 된다.

각 repository 사이에서 상호작용하는 과정은 다음과 같은 것들이 있다. 다른 사람이 하는 것은 생각하지 않도록 하자.

  1. 다른 사람의 remote repository(2)를 나의 remote repository(1)로 가져오는 것(fork)
  2. 나의 remote repository(1)을 나의 local repository(3)으로 가져오는 것(clone)
  3. 나의 local repository(3)의 변경사항을 나의 remote repository(1)에 반영하는 것(push)
  4. Fork로 가져온 프로젝트인 나의 local repository(3)의 변경사항을 나의 remote repository(1)에 반영시킨 후(push), 다른 사람의 remote repository(2)에 반영하는 것(pull request). 이를 GitHub 프로젝트에 기여했다고 한다.

Init, Clone

프로젝트를 시작하는 과정은 다음과 같다.

  1. 먼저 local에서 directory를 하나 생성한다. 이름은 프로젝트 이름으로 한다.
  2. 생성한 directory에서 git init 명령을 입력한다.
  3. 브라우저에서 git repository를 하나 생성한다.
  4. 브라우저에 보이는 안내를 따르면 된다. git remote add origin ... 명령을 입력한다.
  5. 다음 Add, Commit, Push과정을 따르면 된다.

이미 일부 혹은 전체가 만들어져 있는 프로젝트를 local에 받아와서 하고 싶을 때가 있다. 이는 다음 과정을 따른다.

  1. git clone ... 명령으로 remote repository를 나의 local repository(3)으로 받아온다.
  2. 끝. 이제 개발을 시작하면 된다.

Add, Commit, Push

여러분이 혼자서 간단한 프로젝트를 진행하게 된다면 가장 많이 쓰게 되는 명령들이다.

앞에서 말한 repository 상호작용 과정 중 3번을 가장 많이 하게 되는데, 이는 총 4단계로 이루어진다. 물론 경우에 따라 다른 과정이 추가될 수도 있다.

  1. 파일을 프로젝트 목적에 맞게 수정하고 저장한다. 즉 개발 과정이다.
  2. Add: 이제 파일을 cache에 잠시 올려 놓는다. 이 과정이 필요한 이유는, 하나의 commit(한번에 반영할 수정사항)에 여러분이 원하는 파일만 반영할 수 있도록 하기 위함이다. 만약에 반강제적으로 모든 파일이 반영되어야만 한다면, commit이 제 역할을 하지 못하게 될 수 있다.
  3. Commit: 이제 원하는 만큼의 수정사항을 하나의 commit으로 묶는다.
  4. Push: 이제 commit을 진짜로 나의 remote repository에 반영하는 과정이다.

Commit에는 단지 수정사항을 정리하는 것 외에 해주어야 하는 것이 두 가지 더 있다.

  • Commit message: commit할 때 같이 작성한다. Commit message란 이 commit이 어떤 수정사항을 담고 있는지를 알려주는 것이다. 자세히 쓸수록 좋다.
  • Tag: 여러분이 생각하는 그 태그 맞다. 블로그의 글에 달려 있는 태그랑 같은 기능을 한다. 포스팅 대신 commit을 참조하는 것이 다를 뿐이다.

Branch 브랜치

새로운 기능을 개발하거나 테스트를 할 때 사용하는 독립적인 commit history이다. 나무에서 메인 줄기가 아닌 옆으로 빠져나온 나뭇가지를 생각하면 된다.

Branch가 필요한 이유는 무엇인가? 혼자서 간단한 것을 할 때라면 사실 branch를 새로 만들 것도 없이 그냥 진행해도 별 문제는 없다. 하지만 프로젝트의 규모가 커지거나 여러 사람이 협업해야 한다면 branch는 필수이다. 모두가 master branch(메인 줄기)를 직접 수정하려고 들면 큰일난다.

모든 Git 프로젝트는 기본적으로 master branch를 갖는다. master branch가 나무의 메인 줄기로서, 검증이 끝난 프로젝트의 결과물이라 할 수 있다.

branch 간 상호작용은 꽤 종류가 많지만, 여기서는 몇 가지만 간략히 소개한다.

  1. branch에서 새 branch를 생성하는 것(git branch ...)
  2. 어떤 branch에서 다른 특정 branch로 옮겨가는 것(checkout)
  3. 검증이 끝난 branch를, 그 branch를 생성한 주 branch에 합치는 것(merge)

새로운 기능을 개발하여 추가하는 과정은 대개 위의 세 과정을 따른다. 물론 2번과 3번 사이에 개발 과정이 있을 것이다.

이렇게 새로운 기능을 개발하는 branch를 feature(topic) branch라 부른다. 또 구버전 소프트웨어 지원 등의 이유로 별도의 branch가 필요한 경우 이를 release branch라 부른다.

Issue

  • 기능에 대해 논의하거나
  • 버그 수정사항을 알리거나
  • todoList로 활용한다.

협업할 때는 당연히 필요하고, 혼자 할 때도 bugList와 todoList로 쓰면 유용하다.

Git 명령어

GitHub 사용법 - 00. Command List에서 원하는 명령어를 찾아 볼 수 있다.

Comment  Read more

GitHub 사용법 - 00. Command List

29 Jun 2018 | GitHub usage
명령어 설명
git init local repo를 생성한다.
git status [-s] 현재 local branch의 git 상태를 확인한다(수정 파일, cache, commit 등) -s 옵션은 간략히 표시한다.
   
git add <file | directory> stage에 파일이나 디렉토리 혹은 전체(*)를 올린다.
git add -p|-i|-u 각각 부분/대화형/수정 사항을 stage에 추가
git rm --cached <file | directory> 파일이나 디렉토리를 cache에서 제거한다.
git commit [-m “commit message”\ 수정사항들을 하나의 커밋으로 묶고 커밋 메시지를 작성한다.
git commit -v git diff 명령을 포함하는 커밋 메시지 편집창을 열어 커밋한다.
git diff [HEAD] 마지막 커밋과 현재 수정사항 사이의 차이를 보여준다.
git diff [<branch1>] <branch2> 다른 브랜치와의 차이를 보여준다.
git diff [<commit1>] <commit1> 다른 커밋과의 차이를 보여준다.
   
git tag <tag> [-a [-m] ] 마지막 커밋에 태그를 붙인다. -a 옵션은 Annotated 태그를 가리킨다. -m 옵션은 메시지를 작성한다.
git tag <tag> <commit> 지정한 코드에 해당하는 커밋에 태그를 붙인다.
git tag 태그 목록을 보여준다.
git show <tag> 해당 태그에 대한 자세한 설명을 보여준다.
   
git remote add origin <remote repo 주소> local branch를 remote branch와 연결시킨다.
git clone <remote repo 주소> remote repo의 파일 복제본을 local로 가져온다. local repo가 생성된다.
   
git log [--oneline] 현재 브랜치의 commit log를 표시한다. --oneline 옵션은 한줄로 간략히 표시한다.
git log origin/master..[HEAD] remote repo에는 없고 HEAD에는 있는 커밋을 표시한다.
git log --graph 현재 브랜치의 commit log를 그래프 형태로 보여준다.
   
git branch [--list | -r -a] local/remote/전체 repo의 branch 목록 조회
git checkout [-b] <branch> 선택한 branch로 이동. -b 옵션은 브랜치를 생성하면서 이동
git checkout -t [-b] <origin\/branch> 선택한 remote branch의 파일을 다운로드하면서 checkout
git branch -d[-D] <branch> 선택한 local branch 삭제, -D 옵션은 강제 삭제
git push -d origin <branch> remote branch 삭제
git fetch remote branch 목록 업데이트
   
git merge <branch> 현재 브랜치에서 해당 브랜치의 수정사항을 가져온다.
git merge <branch1> <branch2> branch2의 변경사항을 branch1로 가져온다.
git rebase <branch> 현재 브랜치의 base를 해당 브랜치의 tip으로 설정하여, 해당 브랜치의 변경사항을 가져온다.
기타 명령어 설명
git help [<command>]
git [<command>] --help
man git-[<commmand>]		 명령어에 대한 도움말을 볼 수 있다.
git config [--global] user.name “Your name” local repo의 git id(name)을 Your name으로 설정한다. --global 옵션을 주면 모든 local repo에 적용한다.
git config [--global] user.name “Your name” local repo의 git email을 Your email으로 설정한다. --global 옵션을 주면 모든 local repo에 적용한다.
git config [--list | <config settings> \ config 세팅 상태를 볼 수 있다. --list 옵션은 config 세팅 전부를 보여준다.
git config --global color.ui “auto” Git의 출력결과 색상을 활성화
git config --global credential.helper store 비밀번호 저장
git config --global credential.helper cache –timeout “seconds” seconds 초 동안 비밀번호 저장
Comment  Read more

Github blog 수식 입력 방법

29 Jun 2018 | Equation usage

이 글에서는 수식 입력방식을 설명한다.

참조: stackexchange.com

수식 입력은

inline style: $ \sum_{i=0}^n i^2 = \frac{(n^2+n)(2n+1)}{6} $

$ \sum_{i=0}^n i^2 = \frac{(n^2+n)(2n+1)}{6} $

display style: $$ \sum_{i=0}^n i^2 = \frac{(n^2+n)(2n+1)}{6} $$

[\sum_{i=0}^n i^2 = \frac{(n^2+n)(2n+1)}{6}]

로 한다.

참고: newline은 display style에서만 유효하다.

$$ \begin{eqnarray} a^2 + b^2 &=& c^2 \\ &=& 5 \end{eqnarray} $$

[\begin{eqnarray} a^2 + b^2 &=& c^2 \ &=& 5 \end{eqnarray}]

$$ \Delta s = \Biggl\{ \begin{matrix} A \\ B \end{matrix} $$

[\Delta s = \Biggl{ \begin{matrix} A+B \ C \end{matrix}]

Equation Code Display
NewLine \\ $ \ $
Greek small Letters 1 \alpha, \beta, \gamma, \delta, \epsilon, \varepsilon, \zeta, \eta, \theta, \vartheta, \iota, \kappa, \lambda, \mu $ \alpha, \beta, \gamma, \delta, \epsilon, \varepsilon, \zeta, \eta, \theta, \vartheta, \iota, \kappa, \lambda, \mu $
Greek small Letters 2 \nu, \xi, \pi, \rho, \varrho, \sigma, \tau, \upsilon, \phi, \varphi, \chi, \psi, \omega $ \nu, \xi, \pi, \rho, \varrho, \sigma, \tau, \upsilon, \phi, \varphi, \chi, \psi, \omega $
Greek Capital Letters \Gamma, \Delta, \Theta, \Lambda, \Xi, \Pi, \Sigma, \Upsilon, \Phi, \Psi, \Omega $ \Gamma, \Delta, \Theta, \Lambda, \Xi, \Pi, \Sigma, \Upsilon, \Phi, \Psi, \Omega $
Super/subscripts x_i^2, x_{i^2}, \log_2 x, 10^{10}, x^{y^z} $ x_i^2, x_{i^2}, \log_2 x, 10^{10}, x^{y^z} $
Parentheses 1 (\frac{1}{2}), \left(\frac{1}{2}\right) $ (\frac{1}{2}), \left(\frac{1}{2}\right) $
Parentheses 2 (x) {x} [x] |x| \vert x \vert \Vert x \Vert $ (x) {x} [x] |x| \vert x \vert \Vert x \Vert $
Parentheses 3 \langle x \rangle \lceil x \rceil \lfloor x \rfloor $ \langle x \rangle \lceil x \rceil \lfloor x \rfloor $
Parentheses 4 \Biggl(\biggl(\Bigl(\bigl((x)\bigr)\Bigr)\biggr)\Biggr) $ \Biggl(\biggl(\Bigl(\bigl((x)\bigr)\Bigr)\biggr)\Biggr) $
Parentheses 5 \Biggl{\biggl{\Bigl{\bigl{ \lbrace x \rbrace \bigr}\Bigr}\biggr}\Biggr} $ \Biggl{\biggl{\Bigl{\bigl{ \lbrace x \rbrace \bigr}\Bigr}\biggr}\Biggr} $
Parentheses 6 \Biggl[\biggl[\Bigl[\bigl[[x]\bigr]\Bigr]\biggr]\Biggr] $ \Biggl[\biggl[\Bigl[\bigl[[x]\bigr]\Bigr]\biggr]\Biggr] $
Combinations {n+1 \choose 2k} , \binom{n+1}{2k} $ {n+1 \choose 2k} , \binom{n+1}{2k} $
Fraction \frac{(n^2+n)(2n+1)}{6}, {a+1\over b+1}, \cfrac{a}{b} $ \frac{(n^2+n)(2n+1)}{6}, {a+1\over b+1}, \cfrac{a}{b} $
Sigma \sum_{i=0}^n i^2 = \frac{(n^2+n)(2n+1)}{6} $ \sum_{i=0}^n i^2 = \frac{(n^2+n)(2n+1)}{6} $
Signs \infty \prod \int \bigcup \bigcap \iint \iiint \sqrt{x} $ \infty \prod \int \bigcup \bigcap \iint \iiint \sqrt{x} $
Special functions \lim_{x\to 0} \sin \max \ln \log $ \lim_{x\to 0} \sin \max \ln \log $
Matrix 1 \begin{matrix}a & b \\ c & d\end{matrix} $\begin{matrix}a & b \ c & d\end{matrix}$
Matrix 2 \begin{pmatrix}a & b & c \\ d & e & f \\ g \end{pmatrix} $\begin{pmatrix}a & b & c \ d & e & f \ g \end{pmatrix}$
Multi-lines \begin{eqnarray} a^2 + b^2 &=& c^2 \ &=& 5 \end{eqnarray} 표 위쪽 참조.
Inequality \lt \gt \le \leq \leqq \leqslant \ge \geq \geqq \geqslant \neq \gg \ll \ggg \lll $ \lt \gt \le \leq \leqq \leqslant \ge \geq \geqq \geqslant \neq \gg \ll \ggg \lll $
Approximate \approx \sim \simeq \cong \equiv \prec \lhd $ \approx \sim \simeq \cong \equiv \prec \lhd $
Set Inclusion \cup \cap \setminus \subset \subseteq \subsetneq \supset \in \notin \emptyset \varnothing $ \cup \cap \setminus \subset \subseteq \subsetneq \supset \in \notin \emptyset \varnothing $
Logic \land \lor \lnot \forall \exists \nexists \top \bot \vdash \vDash \complement $ \land \lor \lnot \forall \exists \nexists \top \bot \vdash \vDash \complement $
Operations 1 \times \div \pm \mp x \cdot y $ \times \div \pm \mp x \cdot y $
Operations 2 \star \ast \odot \oslash \oplus \otimes \Box \boxtimes \circ \bullet $ \star \ast \odot \oslash \oplus \otimes \Box \boxtimes \circ \bullet $
Arrows 1 \to \rightarrow \leftarrow \leftrightarrow \mapsto \longmapsto $ \to \rightarrow \leftarrow \leftrightarrow \mapsto \longmapsto $
Arrows 2 \leftharpoonup \rightharpoonup \leftharpoondown \rightharpoondown \rightleftharpoons $ \leftharpoonup \rightharpoonup \leftharpoondown \rightharpoondown \rightleftharpoons $
Arrows 3 \uparrow \downarrow \nearrow \searrow \swarrow \nwarrow $ \uparrow \downarrow \nearrow \searrow \swarrow \nwarrow $
Arrows 4 \Rightarrow \Leftarrow \Leftrightarrow \Uparrow \Downarrow \Updownarrow $ \Rightarrow \Leftarrow \Leftrightarrow \Uparrow \Downarrow \Updownarrow $
Modulo a\equiv b\pmod n $ a\equiv b\pmod n $
Ellipsis \ldots, \cdots $ \ldots, \cdots $
Transpose \intercal \top \mid $ \intercal \top \mid $
Spaces 1 \ 2 \quad 3 \qquad 4 $ 1 \ 2 \quad 3 \qquad 4 $
Accents \hat{x} \widehat{xy} \bar{x} \overline{xyz} \vec{x} \overrightarrow{xy} \overleftrightarrow{xy} \dot{x} \ddot{x} $ \hat{x} \widehat{xy} \bar{x} \overline{xyz} \vec{x} \overrightarrow{xy} \overleftrightarrow{xy} \dot{x} \ddot{x} $
Special Characters 1 \backslash \_ \lrace \rbrace $\backslash$ _ $\lbrace \rbrace$
Plain text \text{text…} $ \text{text…} $
Special Characters 2 \infty \aleph_0 \nabla \partial \Im \Re \surd \triangle \square \blacksquare $ \infty \aleph_0 \nabla \partial \Im \Re \surd \triangle \square \blacksquare $
Fonts l \ell \it{l} \boldsymbol{l} \pmb{l} $ l \quad \ell \quad \it{l} \quad \boldsymbol{l} \quad \pmb{l} $
mathbb \mathbb{A} $ \mathbb{ABCDEFGHIJKLMNOPQRSTUVWXYZ} $
mathbb \mathbb{a} $ \mathbb{abcdefghijklmnopqrstuvwxyz} $
mathbf \mathbf{A} $ \mathbf{ABCDEFGHIJKLMNOPQRSTUVWXYZ} $
mathbf \mathbf{a} $ \mathbf{abcdefghijklmnopqrstuvwxyz} $
mathtt \mathtt{A} $ \mathtt{ABCDEFGHIJKLMNOPQRSTUVWXYZ} $
mathtt \mathtt{a} $ \mathtt{abcdefghijklmnopqrstuvwxyz} $
mathrm \mathrm{A} $ \mathrm{ABCDEFGHIJKLMNOPQRSTUVWXYZ} $
mathrm \mathrm{a} $ \mathrm{abcdefghijklmnopqrstuvwxyz} $
mathsf \mathsf{A} $ \mathsf{ABCDEFGHIJKLMNOPQRSTUVWXYZ} $
mathsf \mathsf{a} $ \mathsf{abcdefghijklmnopqrstuvwxyz} $
mathcal \mathcal{A} $ \mathcal{ABCDEFGHIJKLMNOPQRSTUVWXYZ} $
mathcal \mathcal{a} $ \mathcal{abcdefghijklmnopqrstuvwxyz} $
mathscr \mathscr{A} $ \mathscr{ABCDEFGHIJKLMNOPQRSTUVWXYZ} $
mathscr \mathscr{a} $ \mathscr{abcdefghijklmnopqrstuvwxyz} $
mathfrak \mathfrak{A} $ \mathfrak{ABCDEFGHIJKLMNOPQRSTUVWXYZ} $
mathfrak \mathfrak{a} $ \mathfrak{abcdefghijklmnopqrstuvwxyz} $

Mathjax 참고

Comment  Read more

Stack(스택)

29 Jun 2018 | Stack

참조

분류 URL
문제 스택, 괄호
응용 문제 스포일러 문제
이 글에서 설명하는 라이브러리 std::stack

개요

시간복잡도: $ O(M) $

공간복잡도: $ O(N) $

  • N은 원소의 수, M은 연산의 수이다.
  • 스택 자체는 알고리즘이 아닌 자료구조이지만, 스택을 쓰는 경우 복잡도는 위와 같이 나온다.

이 글에서는 스택(stack)이라고 하는 자료구조와, 이를 활용한 문제들을 살펴볼 것이다.

스택은 간단하면서도 매우 유용한 자료구조이다. 여러분의 실생활에서도 자주 볼 수 있는 개념이다.
그리고 알고리즘으로 적용하기에도 쉽다. 그럼 스택은 무엇인가?

Stack(스택)

스택(stack)의 사전적 의미는 더미(무더기)이다.

스택은 다음 그림으로 설명된다.

Stack

책상 위에 책을 몇 권 쌓는 것과 같다. 1번 책을 쌓고, 2번 책을 쌓고, … , 6번 책까지 쌓았다고 하자.
그리고 책을 한 권을 집는다고 치자. 그러면 여러분은 (정상적이라면) 몇 번 책을 집겠는가?
사서 고생하는 사람이 아니라면 굳이 아래쪽 책을 힘들게 빼진 않을 것이다. 즉, 6번 책을 뺄 것이다. 위의 그림과 갈다.
첫 번째 pop(책을 빼는 것) 연산은 가장 마지막에 들어온 6번부터 행해진다.

이것을 Last-In-First-Out이라 부른다. 즉 가장 나중에 들어온 것이 제일 먼저 나간다는 의미이다.
이것이 스택의 전부이다. 그리고 C++의 STL에는 이것이 친절히 구현되어 있다. 다음에서 살펴보자.

std::stack 사용법

Include

우선 include를 해야 한다. 특별히 큰 프로젝트에서 쓰는 것이 아니라면, std::를 매번 쓰기 귀찮으니 namespace도 써 주자.

#include <stack>

using namespace std;

선언

stack은 generic으로 구현된 template이다. 즉, stack에 들어갈 데이터 타입을 정해야 한다.
보통 int나 char 등을 사용하게 될 것이다. 물론 기본형 뿐만 아니라 사용자 정의 타입도 가능하다.

stack<int> st; // 현재 비어 있다.
// stack<char> st_c;
// stack<dot_2d> st_person; // dot_2d는 알아서 정의하시길...

push(e)

스택에 무언가를 집어넣는(push) 연산이다. e는 집어넣을 원소이다.

st.push(10);  // 10
st.push(20);  // 10 20
st.push(30);  // 10 20 30
st.push(777); // 10 20 30 777

size()

스택의 현재 size를 반환한다. 몇 개나 들어 있는지 알고 싶을 때 쓰면 된다.

printf("size: %d\n", st.size());  // size: 4
st.push(999);
printf("size: %d\n", st.size());  // size: 5

top()

스택의 맨 위 원소를 반환한다. 스택에서는 맨 위의 것만 빼낼 수 있다. 다른 원소에는 접근이 불가능하다.
물론 스택을 직접 구현한다면 접근 가능하게 할 수도 있지만, 스택을 쓰는 데 그렇게 할 이유가..?

int e = st.top();
printf("top: %d\n", e);   // top: 999

pop()

스택의 맨 위 원소를 제거한다. 책을 하나 가져갔다고 생각하면 된다.
반환값이 void이므로 리턴값으로 top 값을 알아낼 수는 없다.
또, 비어 있는데 pop을 수행하려고 하면 런타임 에러를 발생시킨다.

st.pop(); // 999가 제거됨
for (int i = 0; i < 3; i++)
    st.pop(); 
// 777, 30, 20이 차례로 제거됨

empty()

스택이 비었는지를 검사한다. size() == 0 구문으로 체크할 수도 있지만, 이쪽이 더 직관적이다. 그리고 생각보다 자주 쓰게 된다.

if (st.empty())
    printf("stack is empty, 1\n");
st.pop();   // 10이 제거됨
if (st.empty())
    printf("stack is empty, 2\n");

// stack is empty, 2

emplace(e)

STL에서 emplace는 생성자를 호출하면서 push(혹은 push_back)하는 것과 동일하다.
이 기능은 stack에 기본형 말고 dot_2d와 같은 사용자 정의 함수나 생성자 호출이 필요한 데이터 타입을 넣었을 때 필요하다.
int와 같은 기본형을 넣을 때는 별 차이가 없다.

st.emplace(-3);
printf("top: %d\n", st.top());  // top: -3

swap(another_stack)

같은 데이터 타입을 담고 있는 다른 스택과 원소 전체를 swap한다.

stack<int> another_st;
st.swap(another_st);
if (st.empty())
    printf("stack is empty, 3\n");
// stack is empty, 3

스택은 사실상 이게 전부이다. 그리고 생각보다 많은 문제를 풀 수 있다.
물론 대부분은 너무 뻔히 풀이가 스택이라는 것이 보이지만, 안 그런 것도 있다(스포일러 문제 참조)

문제 풀이

BOJ 10828(스택)

문제: 스택

풀이: BOJ 10828(스택) 문제 풀이

BOJ 09012(괄호)

문제: 괄호

풀이: BOJ 09012(괄호) 문제 풀이

스포일러 문제

문제: 스포일러 문제

풀이: 스포일러 풀이

Comment  Read more