이 글에서는 2016년 6월 Sebastian Nowozin 등이 발표한 f-GAN - Training Generative Neural Samplers using Variational Divergence Minimization를 살펴보도록 한다.

f-GAN은 특정한 구조를 제안했다기보다는 약간 divergence에 대한 내용을 일반적으로 증명한 수학 논문에 가깝다.

중요한 부분만 적을 예정이므로 전체가 궁금하면 원 논문을 찾아 읽어보면 된다.

이 논문은 수학이 넘쳐흐르는 논문이다.

f-GAN

논문 링크: f-GAN

초록(Abstract)

2016년에 나온 논문임을 생각하라.

Generative neural sampler는 random input vector를 입력으로 받아 network weights에 정의된 확률분포로부터 sample을 만들어내는 확률적 모델이다. 이 모델들은 sample과 도함수 계산이 효율적이지만 우도(likelihood)나 주변화(marginalization)을 계산하진 못한다. 적대생성적 학습방법은 이런 모델이 추가 신경망을 통해 이를 학습할 수 있게 해준다.
우리는 이 적대생성적 접근법이 더 일반적인 변분 발산(variational divergence) 추정 접근의 특별한 경우임을 보일 것이다. 우리는 임의의 f-divergence가 Generative neural sampler에 쓰일 수 있음을 보일 것이다. 우리는 이렇게 다양한 divergence 함수를 쓸 수 있는 것이 학습 복잡도와 생성모델의 품질 면에서 이득임을 논할 것이다.

서론(Introduction)

확률적 생성모델은 주어진 domain $\chi$ 상의 확률분포를 서술한다. 예를 들면 자연언어 문장, 자연 이미지, 녹음된 파형 등의 분포가 있다.

가능한 모델 집합 $Q$에서 생성모델 Q가 주어졌을 때 우리는 일반적으로 다음에 관심이 있다:

Sampling. Q로부터 sample을 생성한다. sample을 살펴보거나 어떤 함숫값을 계산해봄으로써 우리는 분포에 대한 통찰을 얻거나 결정문제를 풀 수 있다.
Estimation. 알려지지 않은 진짜 분포 P로부터 iid sample ${x_1, x_2, …, x_n}$이 주어졌을 때, 이 진짜 분포를 가장 잘 설명하는 Q $\in Q$를 찾는다.
Point-wise 우도 측정. sample $x$가 주어지면, 우도 Q($x$)를 계산한다.

GAN은 정확한 sampling과 근사추정이 가능한 인상적인 모델이다. 여기서 사용된 모델은 균등분포 같은 random input vector를 받는 feedforward 신경망이다. 최종적으로 모델을 통과하여 나오는 것은 예를 들면 이미지이다. GAN에서 sampling하는 것은 딱 1개의 input이 신경망을 통과하면 정확히 하나의 sample이 나온다는 점에서 효율적이다.

이런 확률적 feedforward 신경망을 generative neural samplers라고 부를 것이다. GAN도 여기에 포함되며, 또한 variational autoencoder의 decoder 모델이기도 하다.

original GAN에서, neural sample를 JSD의 근사적 최소화로 추정하는 것이 가능함이 증명되어 있다.

\[D_{JS}(P \| Q) = {1 \over 2} D_{KL}(P \| {1 \over 2}(P+Q)) + {1 \over 2} D_{KL}(Q \| {1 \over 2}(P+Q))\]

$D_{KL}$은 Kullback–Leibler divergence이다.

GAN 학습의 중요한 테크닉은 동시에 최적화된 Discriminator 신경망을 만든 것에 있다. 왜냐하면 $D_{JS}$는 진짜 분포 $P$는 충분한 학습을 통해 Q가 $P$에 충분히 가까워졌을 때 분포 간 divergence를 측정하는 적정한 방법이기 때문이다.

우리는 이 논문에서 GAN 학습목적(training objectives)과 이를 임의의 f-divergence로 일반화하고자, GAN을 variational divergence 추정 framework로 확장할 것이다.

구체적으로, 이 논문에서 보여주는 state-of-the-art한 것은:

GAN 학습목적을 모든 f-divergence에 대해 유도하고 여러 divergence 함수를 소개할 것이다: Kullback-Leibler와 Pearson Divergence를 포함한다.
우리는 GAN의 saddle-point 최적화를 단순화할 것이고 또 이론적으로 증명할 것이다.
자연 이미지에 대한 generative neural sampler을 측정하는 데 어느 divergence 함수가 적당한지 실험적 결과를 제시하겠다.

방법(Method)

먼저 divergence 추정 framework를 리뷰부터 하겠다. 이후 divergence 추정에서 model 추정으로 확장하겠다.

The f-divergence Family

Kullback-Leibler divergence같이 잘 알려진 것은 두 확률분포 간 차이를 측정한다.

두 분포 $P$와 $Q$가 있고, domain $\chi$에서 연속밀도함수 $p$와 $q$에 대해 f-divergence는
$ f : \mathbb{R}_+ \rightarrow \mathbb{R} $이 $f(1)=0$인 볼록이고 하반연속인(convex, lower-semicontinuous) 함수 $f$에 대해

\[D_f(P \Vert Q) = \int_{\chi} q(x) f \Bigl( {p(x) \over q(x)} \Bigr) dx\]

로 정의된다.

Variational Estimation of f-divergences

Nyugen 등 연구자는 $P$와 $Q$로부터의 sample만 주어진 경우에서 f-divergence를 측정하는 일반적인 변분법을 유도했다. 우리는 이를 고정된 모델에서 그 parameter를 측정하는 것으로까지 확장할 것이고, 이를 variational divergence minimization(VDM)이라 부를 것이다. 또한 적대적 생성 학습법은 이 VDM의 특수한 경우임을 보인다.

모든 볼록이고 하반연속인 볼록 켤레함수 $f^\ast$ (Fenchel conjugate)를 갖는다. 이는

\[f^\ast(t) = \quad sup \quad \{ ut-f(u) \} \\ u \in dom_f \qquad\]

로 정의된다.

또한 $f^\ast$ 역시 볼록이며 하반연속이고 $f^{\ast\ast} = f$이므로 $ f(u) = sup_{t \in dom_{f^\ast}} { tu-f^\ast(t) } $로 쓸 수 있다.

Nguyen 등 연구자는 lower bound를 구했다: $\tau$가 $T: \chi \rightarrow \mathbb{R} $인 함수들의 임의의 집합일 때,

\[D_f(P \Vert Q) \ge sup_{T \in \tau} (\mathbb{E}_{x \sim P} [T(x)] - \mathbb{E}_{x \sim Q} [f^\ast(T(x))])\]

변분법을 취해서,

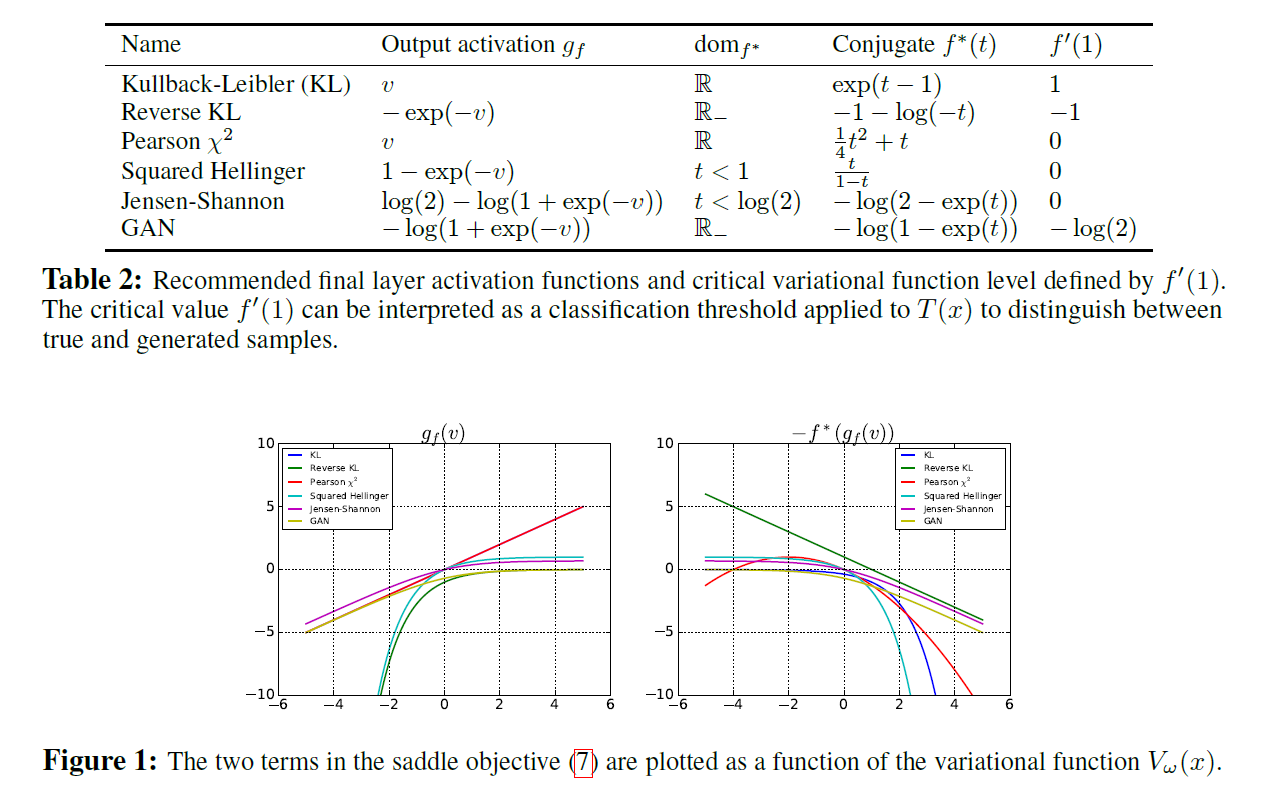
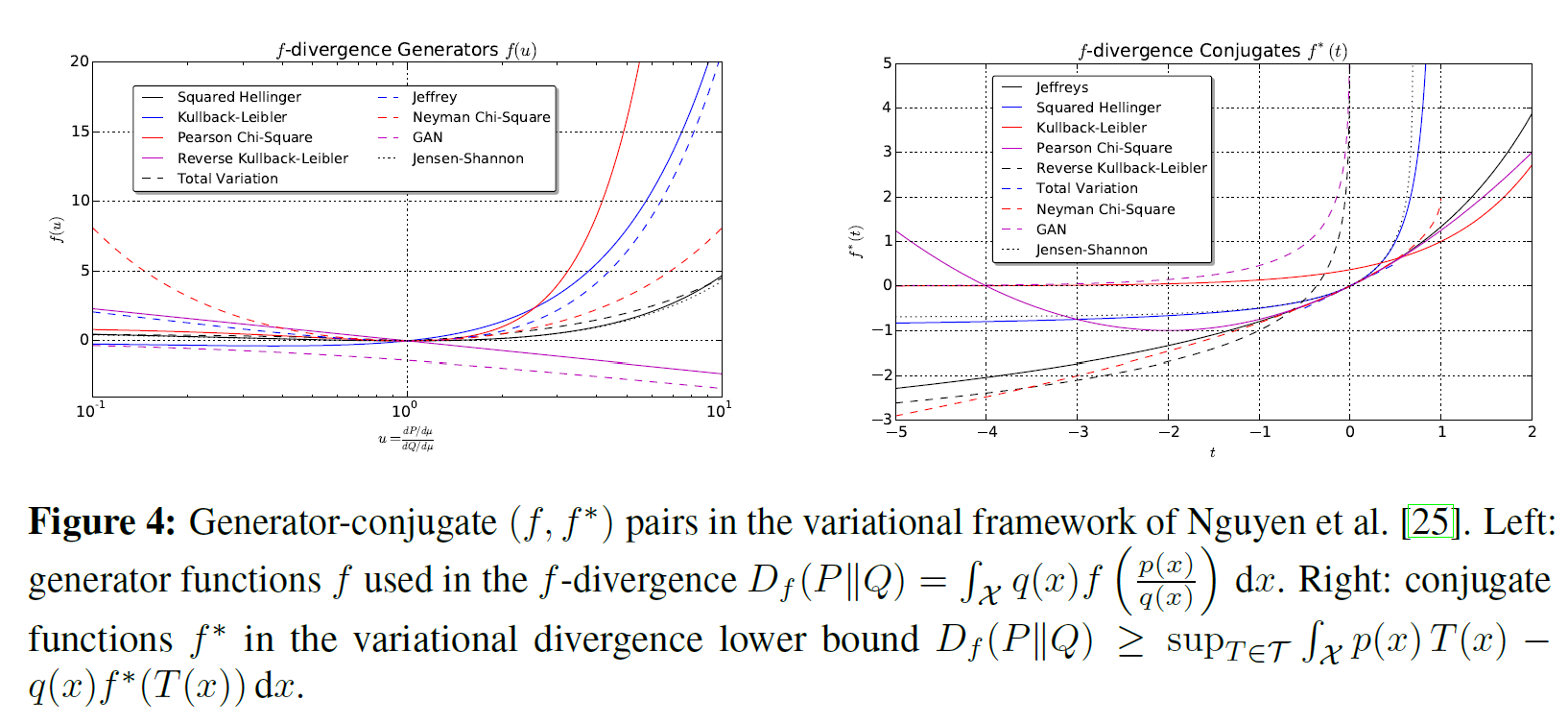
\[T^\ast(x) = f^{'} \Bigl( {p(x) \over q(x)} \Bigr)\]

아래는 여러 f-divergence를 생성함수와 함께 나타낸 것이다.

Variational Divergence Minimization(VDM)

이제 실제 분포 $P$가 주어졌을 때 생성모델 $Q$를 측정하기 위해 f-divergence $D_f(P\Vert Q)$에 하한을 적용할 수 있다.

벡터 $\theta$를 받는 모델 $Q$를 $Q_{\theta}$, $\omega$를 쓰는 $T$를 $T_{\omega}$로 썼을 때, 우리는 다음 f-GAN 목적함수의 saddle-point를 찾는 것으로 $Q_{\theta}$를 학습시킬 수 있다.

\[F(\theta, \omega) = \mathbb{E}_{x \sim P} [T_{\omega}(x)] - \mathbb{E}_{x \sim Q_{\theta}} [f^\ast({T_\omega}(x))]\]

주어진 유한한 학습 데이터셋에 대해 위 식을 최적화하려면, minibatch를 통해 기댓값을 근사해야 한다.

$\mathbb{E}_{x \sim P}[\cdot]$를 근사하기 위해 학습 셋으로부터 비복원추출하여 $B$개를 뽑고,
$\mathbb{E}_{x \sim Q_{\theta}}[\cdot]$를 근사하기 위해 현재 생성모델 $Q_{\theta}$로부터 $B$개를 뽑는다.

Representation for the Variational Function

위의 식을 다른 f-divergence에도 사용하려면 켤레함수 $f^\ast$의 도메인 $dom_{f^\ast}$를 생각해야 한다. $T_\omega (x) = g_f(V_\omega(x)) $로 바꿔 쓸 수 있다.

이제 GAN 목적함수를 보면, divergence가 sigmoid이므로

\[F(\theta, \omega) = \mathbb{E}_{x \sim P} [log D_{\omega}(x)] - \mathbb{E}_{x \sim Q_{\theta}} [log(1-D_\omega(x))]\]

출력 활성함수는 Table 6을 보라(부록).

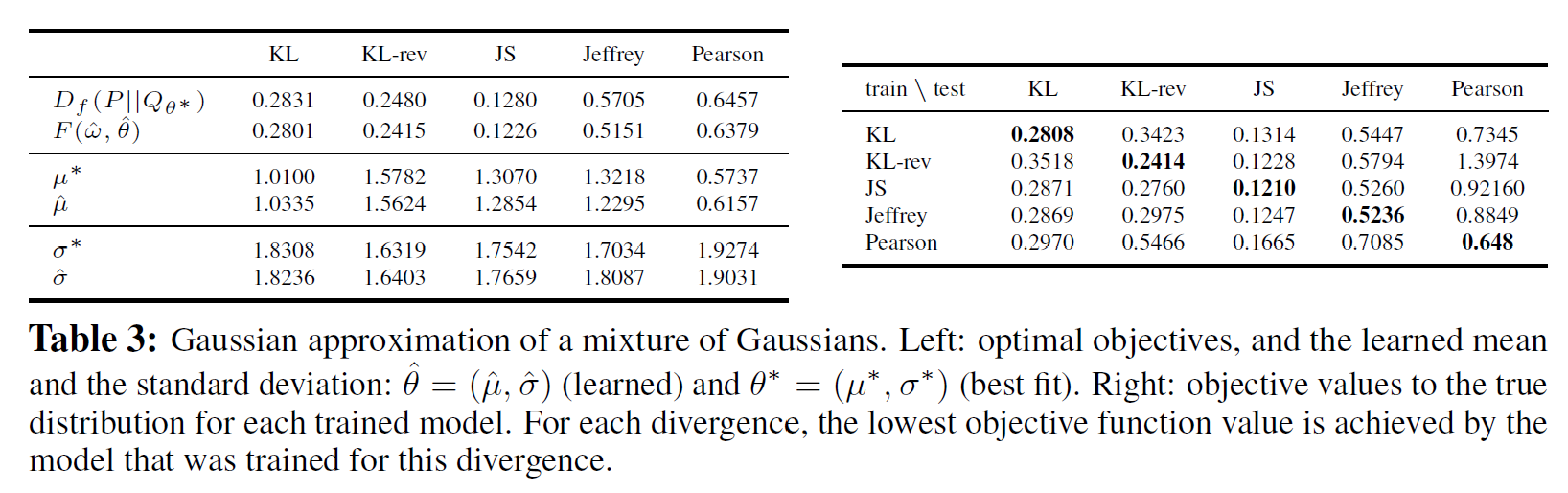
Example: Univariate Mixture of Gaussians

가우시안 sample에 대해 근사한 결과를 적어 놓았다.

VDM 알고리즘(Algorithms for Variational Divergence Minimization(VDM))

이제 우리는 목적함수의 saddle point를 찾기 위한 수치적 방법을 논할 것이다.

Goodfellow가 제안한 교대(alternative) 학습 방법
더 직접적인 single-step 최적화 과정

두 가지를 쓴다.

Single-Step Gradient Method

원래 것과는 달리 inner loop가 없고, 단 하나의 back-propagation으로 $\omega$와 $\theta$의 gradient가 계산된다.

saddle point 근방에서 $\theta$에 대해 볼록하고 $\omega$ 에 대해 오목한 $F$에 대해 위 알고리즘 1은 saddle point $(\theta^\ast, \omega^\ast)$에서 수렴함을 보일 수 있다.

이를 위해 다음 정리를 논문 부록에서 보이고 있다.

Theorem 1. $\pi^t := (\theta^t, \omega^t) $ 라 하고, 조금 위의 근방 조건을 만족하는 saddle point $ \pi^\ast = (\theta^\ast, \omega^\ast) $ 가 존재한다고 가정하자. 더욱이 위 근방에 포함되는 $ J(\pi) = {1\over 2} \Vert \nabla F(\pi) \Vert_2^2 $ 를 정의할 수 있고, $F$는 $ \pi^\ast $ 근방 모든 $ \pi, \pi^{‘} $ 에 대해 $ \Vert \nabla J(\pi^{‘}) - \nabla J(\pi) \Vert_2 \le L \Vert \pi^{‘} - \pi \Vert_2 $ 를 만족하는 상수 $ L > 0 $ 가 존재할 수 있게 하는 $F$는 충분히 smooth하다.
알고리즘 1에서 step-size를 $ \eta=\delta / L$ 라 할 때,

\[J(\pi^t) \le \Bigl( 1 - {\lambda^2 \over 2L} \Bigr)^t J(\pi^0)\]

를 얻을 수 있다.
또 gradient $ \nabla F(x) $ 의 2차 norm은 기하적으로 감소한다.

Practical Considerations

Goodfellow가 GAN 논문 당시 제안한 팁 중에 $ \mathbb{E}_{x \sim Q_{\theta}} [log(1-D_\omega(x))]$를 최소화하는 대신 $ \mathbb{E}_{x \sim Q_{\theta}} [log D_\omega(x)] $를 최대화하는 것으로 속도를 빠르게 하는 것이 있었다.
이를 더 일반적인 f-GAN에 적용하면

\[\theta^{t+1} = \theta^t + \eta \nabla_\theta \mathbb{E}_{x \sim Q_{\theta^t}} [g_f(V_{\omega^t}(x))]\]

그렇게 함으로써 generator 출력을 최대화할 수 있다.

실험적으로, 우리는 Adam과 gradient clipping이 LSUN 데이터셋의 대규모 실험에서는 특히 유용함을 발견하였다.

실험(Experiments)

이제 VDM에 기초하여 MNIST와 LSUN에 대해 학습시킨 결과는 다음과 같다.

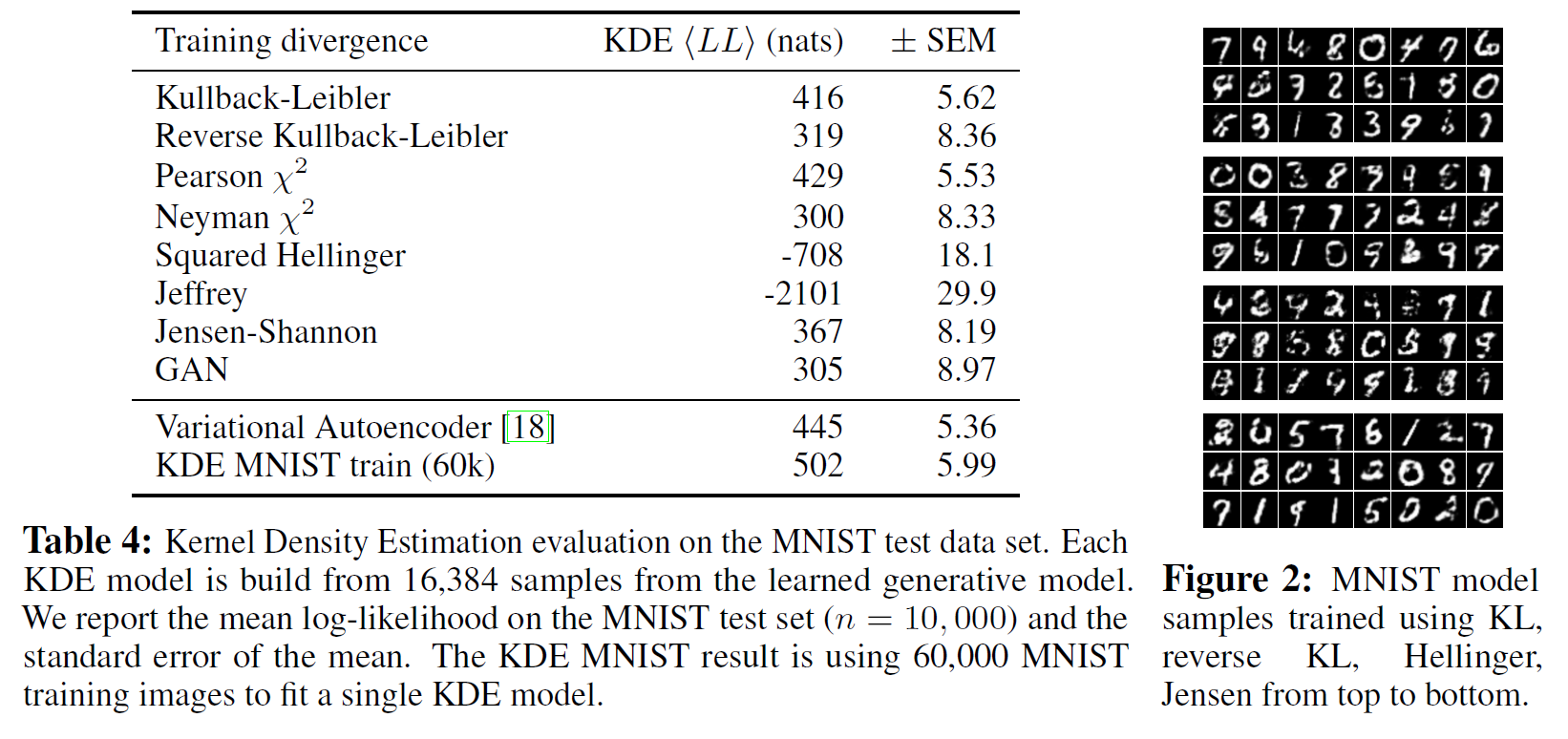
결과 요약을 하면… 약간 예상 외로 divergence 함수가 달라져도 결과의 품질은 큰 차이가 없었다고 한다.

토의(Discussion)

Generative neural samplers는 factorizing 가정 없이도 복잡한 분포를 표현하는 강력한 방법을 제공한다. 그러나 이 논문에서 사용된 순수 generative neural samplers는 관측된 데이터에 대한 조건부로 적용할 수 없고 따라서 그로부터 추론할 것이 없다는 한계를 갖고 있다.

우리는 미래에는 표현의 불확실성을 위한 neural samplers의 진면목이 식별 모델에서 발견될 것이며 생성자와 조건부 GAN 모델에 추가적인 input을 넣음으로써 쉽게 이 경우에 대해 확장할 수 있을 것이라 믿는다.

참고문헌(References)

논문 참조!

부록

Section A: 이 부분이다.
Section B: f-divergence의 확장된 리스트(생성함수와 볼록 켤레함수)를 나열하였다.
Section C: Theorem 1를 증명한다. (논문에는 Theorem 2라 되어 있는데 같은 것이다)
Section D: 현재 GAN 최적화 알고리즘과 차이를 논한다.
Section E: 다양한 divergence 측정방법을 써서 Gaussian을 혼합 Gaussian 분포에 맞춤으로써 우리의 접근법을 증명한다.
Section F: 본문에서 사용한 모델의 세부 구조를 보여준다.

증명의 자세한 부분은 논문을 보는 것이 빠르므로 생략하겠다.

MNIST 생성자:
$z \rightarrow Linear(100, 1200) \rightarrow BN \rightarrow ReLU \rightarrow Linear(1200, 1200) $
$ \rightarrow BN \rightarrow ReLU \rightarrow Linear(1200, 784) \rightarrow Sigmoid $

모든 weights는 0.05 scale로 초기화되었다.

MNIST Variational Function:
$ x \rightarrow Linear(784, 240) \rightarrow ELU \rightarrow Linear(240, 240) \rightarrow ELU \rightarrow Linear(240, 1) $

ELU는 exponential linear unit이다. 모든 weights는 0.005 scale로 초기화되었다.

LSUN Natural Images:
$ z \rightarrow Linear(100, 6\ast6\ast512) \rightarrow BN \rightarrow ReLU \rightarrow Reshape(512, 6, 6) \rightarrow Deconv(512, 256) \rightarrow BN $
$ \rightarrow ReLU \rightarrow Deconv(256, 128) \rightarrow BN \rightarrow ReLU \rightarrow Deconv(128, 64) \rightarrow BN \rightarrow ReLU \rightarrow Deconv(64, 3) $

deconv는 kernel size 4, stride 2를 사용하였다.

Deconv는 Deconvolution을 의미하는데, DCGAN 글에서도 설명하였듯 잘못된 표현이다.

이후 연구들

GAN 이후로 수많은 발전된 GAN이 연구되어 발표되었다.

많은 GAN들(catGAN, Semi-supervised GAN, LSGAN, WGAN, WGAN_GP, DRAGAN, EBGAN, BEGAN, ACGAN, infoGAN 등)에 대한 설명은 다음 글에서 진행하도록 하겠다.

Gorio Tech Blog

f-GAN(f-GAN 논문 설명)

f-GAN

초록(Abstract)

서론(Introduction)