Pix2Pix(Image-to-Image Translation with Conditional Adversarial Networks, Pix2Pix 논문 설명)
07 Apr 2019 | GAN Machine Learning CNN Generative Model Paper_Review목차
- Pix2Pix(Image-to-Image Translation with Conditional Adversarial Networks)
이 글에서는 2016년 11월 Phillip Isola 등이 발표한 Image-to-Image Translation with Conditional Adversarial Networks(Pix2Pix)를 살펴보도록 한다.
Pix2Pix는 Berkeley AI Research(BAIR) Lab 소속 Phillip Isola 등이 2016 최초 발표(2018년까지 업데이트됨)한 논문이다.

Pix2Pix는 Image to Image Translation을 다루는 논문이다. 이러한 변환은 Colorization(black & white $\rightarrow$ color image) 등을 포함하는데, Pix2Pix에서는 이미지 변환 문제를 colorization처럼 한 분야에만 국한되지 않고 좀 더 일반화한 문제를 풀고자 했다. 그리고 그 수단으로써 Conditional adversarial nets를 사용했다.
중요한 부분만 적을 예정이므로 전체가 궁금하면 원 논문을 찾아 읽어보면 된다.
Pix2Pix(Image-to-Image Translation with Conditional Adversarial Networks)
논문 링크: Pix2Pix(Image-to-Image Translation with Conditional Adversarial Networks)
초록(Abstract)
우리는 conditional adversarial networks를 일반화된 이미지 변환 문제에 테스트하였다. 이 네트워크는 단지 input-output mapping만 배우는 것이 아니라 이를 학습하기 위한 loss function까지 배운다. 따라서 전통적으로 매우 다른 loss function을 쓰던 문제에들도 이 접근법을 적용할 수 있다.
우리는 이 접근이 label과 동기화, 경계선만 있는 이미지를 복원, 흑백이미지에 색깔 입히기 등등의 문제에 효과적임을 보였다.
서론(Introduction)
이미지를 이미지로 변환할 뿐인 수많은 문제들은 그 세팅이 똑같음에도 각각 따로 연구되어 왔다(위에서 말한 이미지 변환 문제들). 우리는 이러한 변환 문제를 위한 일반적인 framework를 개발하는 것이 목표이다.
이쪽 방향으로는 이미 CNN이라는 좋은 기계가 있다. CNN은 결과의 품질을 알려주는 loss function을 최소화한다. 그러나 학습 과정 자체는 자동화되어 있지만 결과를 잘 나오게 하기 위해서는 여전히 수동으로 조절해야 할 것이 많다. 즉, 우리는 무엇을 최소화해야하는지 CNN에게 말해주어야 한다.
만약 우리가 단순히 결과와 정답 사이의 유클리드 거리를 최소화하라고만 하면 뿌연(blurry) 이미지를 생성하게 된다. 이는 유클리드 거리는 그럴듯한 결과를 평균했을 때 최소화되기 때문이고, 결과적으로 이미지가 흐려진다. 실제 같은(realistic) 이미지를 얻기 위해서는 더 전문 지식이 필요하다.
만약 우리가 원하는 것을 고수준으로(high-level goal) 말할 수만 있다면, 네트워크는 스스로 그러한 목표에 맞게 loss를 줄여나갈 것이다. 운 좋게도, 최근에 정확히 이것을 해주는 GAN이 발표되었다. GAN은 실제와 가짜를 구분하지 못하도록 학습을 진행하며, 이는 흐린 이미지를 생성하지 않게 할 수 있다(뿌연 이미지는 실제 사진처럼 보일 리 없으므로).
이 논문에서, 우리는 CGAN이라는 조건부 생성모델을 사용한다. 우리는 input image라는 조건을 줄 것이고 그에 맞는 output image를 생성할 것이기 때문에 이는 이미지 변환 문제에 잘 맞는다.
이 논문이 기여하는 바는
- conditional GAN이 넓은 범위의 문제에서 충분히 합리적인 결과를 가져다준다는 것을 밝혔고
- 좋은 결과를 얻기에 충분한 간단한 framework를 제안하고 여러 중요한 architecture의 효과를 분석하였다.
관련 연구(Related Works)
- Structures losses for image modeling: 이미지 변환 문제는 per-pixel 분류 또는 회귀 문제로 다뤄졌다. 이러한 공식화는 output space는 “unstructured”이며 각 결과 픽셀은 다른 픽셀에 독립적인 것처럼 다룬다. CGAN는 “structured loss”를 학습하며 많은 논문들이 이러한 loss를 다룬다. conditional random fields, SSIM metric, nonparametric losses 등등.
- Conditional GANs: 사실 이 논문에서 GAN을 처음 사용한 것은 아니다. 그러나 조건부 GAN을 이미지 변환 문제에 사용한 적은 없었다. CGAN에 대한 설명은 여기를 참조하자.
방법(Method)
GAN은 random noise vector $z$로부터 output image $y$를 생성하는 $G: z \rightarrow y$를 학습하는 생성모델이다. 이에 비해 CGAN은 $z$와 observed image $x$로부터 $y$로의 mapping인 $G: {x, z} \rightarrow y$를 학습한다.
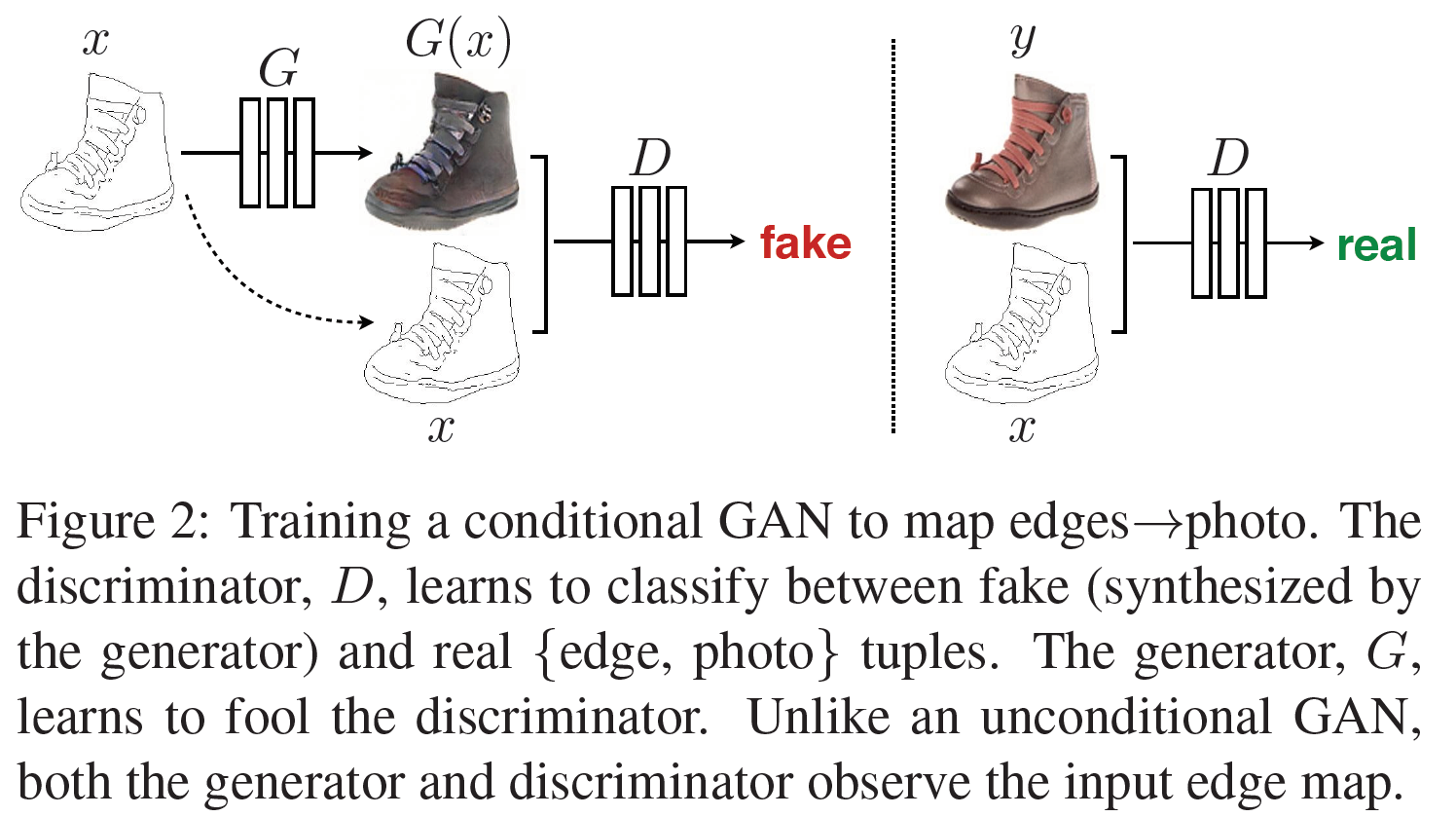
목적함수(Objective)
CGAN의 목적함수는 다음과 같다.
\[\mathcal{L}_{\text{cGAN}}(G, D) = \mathbb{E}_{x , \ y}[log \ D(x,y)] + \mathbb{E}_{x , \ z}[log \ (1-D(G(x, z)))]\]D를 조건부로 학습시키는 것을 중요하게 여겨, D가 $x$를 관측하지 못하도록 unconditional variant를 비교하도록 했다:
\[\mathcal{L}_{\text{GAN}}(G, D) = \mathbb{E}_{ y}[log \ D(y)] + \mathbb{E}_{x , \ z}[log \ (1-D(G(x, z)))]\]D의 할일은 그대로이지만, G는 단지 D를 속이는 것뿐만 아니라 L2 distance에서의 ground truth에도 가깝도록 만들어야 한다.
사실 L2보다는 L1을 사용하는 것이 덜 흐린 이미지를 생성하는 데 도움이 되었다:
그래서 최종 목적함수는
\[G^\ast = arg \ min_G \ max_D \ \mathcal{L}_{\text{cGAN}}(G, D) + \lambda \mathcal{L}_{L1}(G)\]이다.
$z$가 없이도 네트워크는 $x \rightarrow y$ mapping을 학습할 수 있지만, 결정론적인 결과를 생성할 수 있고, 따라서 delta function 이외의 어떤 분포와도 맞지 않을 수 있다. 과거의 conditional GAN은 이를 인정하여 $x$에 더해 Gaussian noise $z$를 입력으로 주었다.
초기 실험에서 우리는 noise를 단순히 무시하도록 했지만, 최종 모델에서는 dropout 시에만 noise를 제공하여 학습과 테스트 시 모두에 G의 여러 레이어에 적용되도록 만들었다. dropout noise에도 불구하고 우리는 매우 조금의 stochasiticity만을 관측하였다. 아주 stochastic한 결과를 생성하는 conditional GAN을 설계하는 것은 아주 중요한 문제이다.
네트워크 구조(Network architectures)
우리는 DCGAN을 G와 D의 기본 모델로 하였고 둘 다 convolution-BatchNorm-ReLU 구조를 따른다.
Generator with skips
이미지 변환(image-to-image translation) 문제에서 어려운 점은 고해상도 input grid를 고해상도 output grid로 mapping하는 것이다. 심지어 표면의 외관은 다른데 각각 같은 근본적인 구조를 가진다는 것이다.
많은 이전 연구들은 encoder-decoder 네트워크를 사용한다. 이러한 네트워크에서는 bottleneck 레이어를 통과하기 때문에 정보의 손실이 필연적으로 발생할 수밖에 없다. 그래서, skip-connection을 추가한 U-Net이라는 구조를 사용했다.
정확히는, 전체 레이어 개수를 $n$이라 할 때 모든 $i$번째 레이어와 $n-i$번째 레이어를 연결했다. 각 연결은 단순히 concatenate한 것이다.
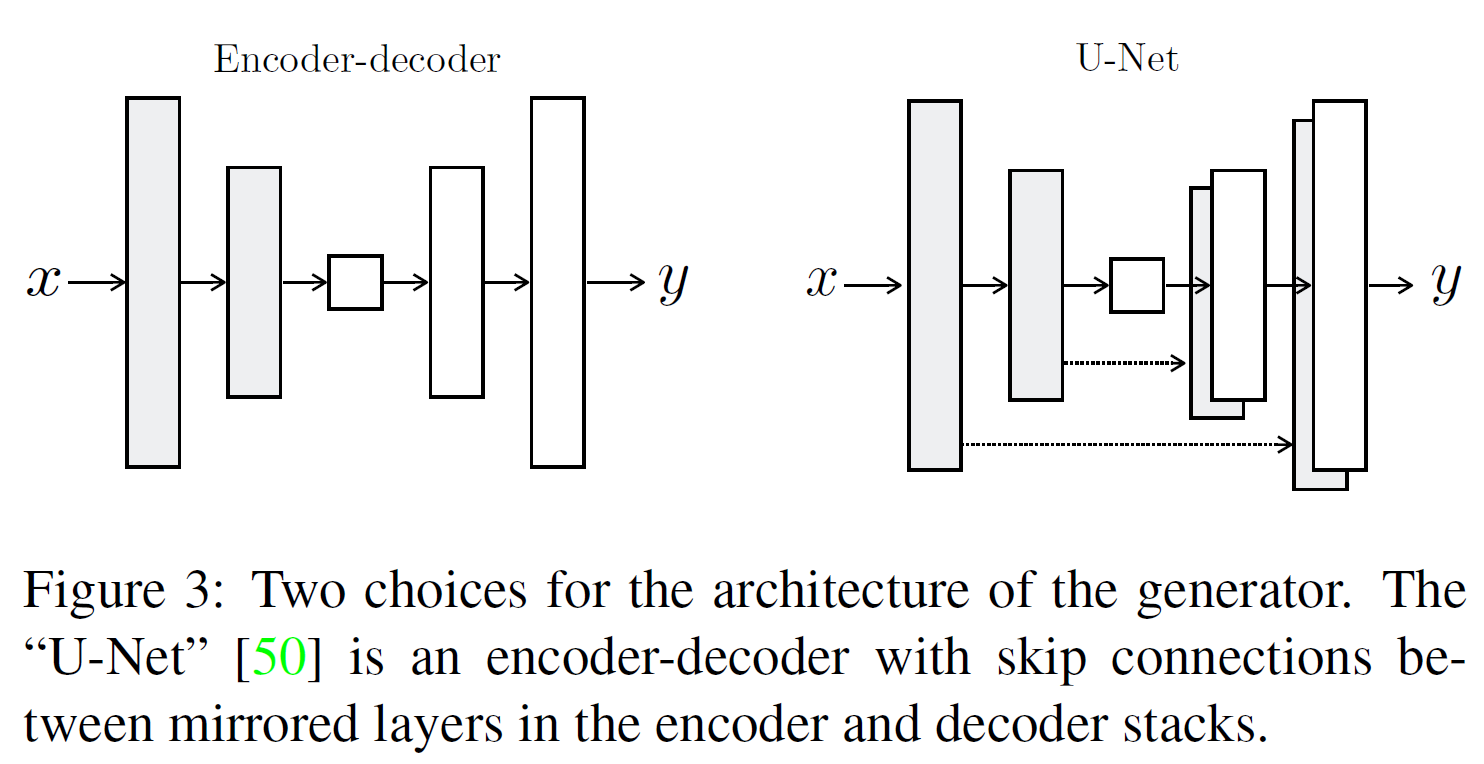
Markovian discriminator(PatchGAN)
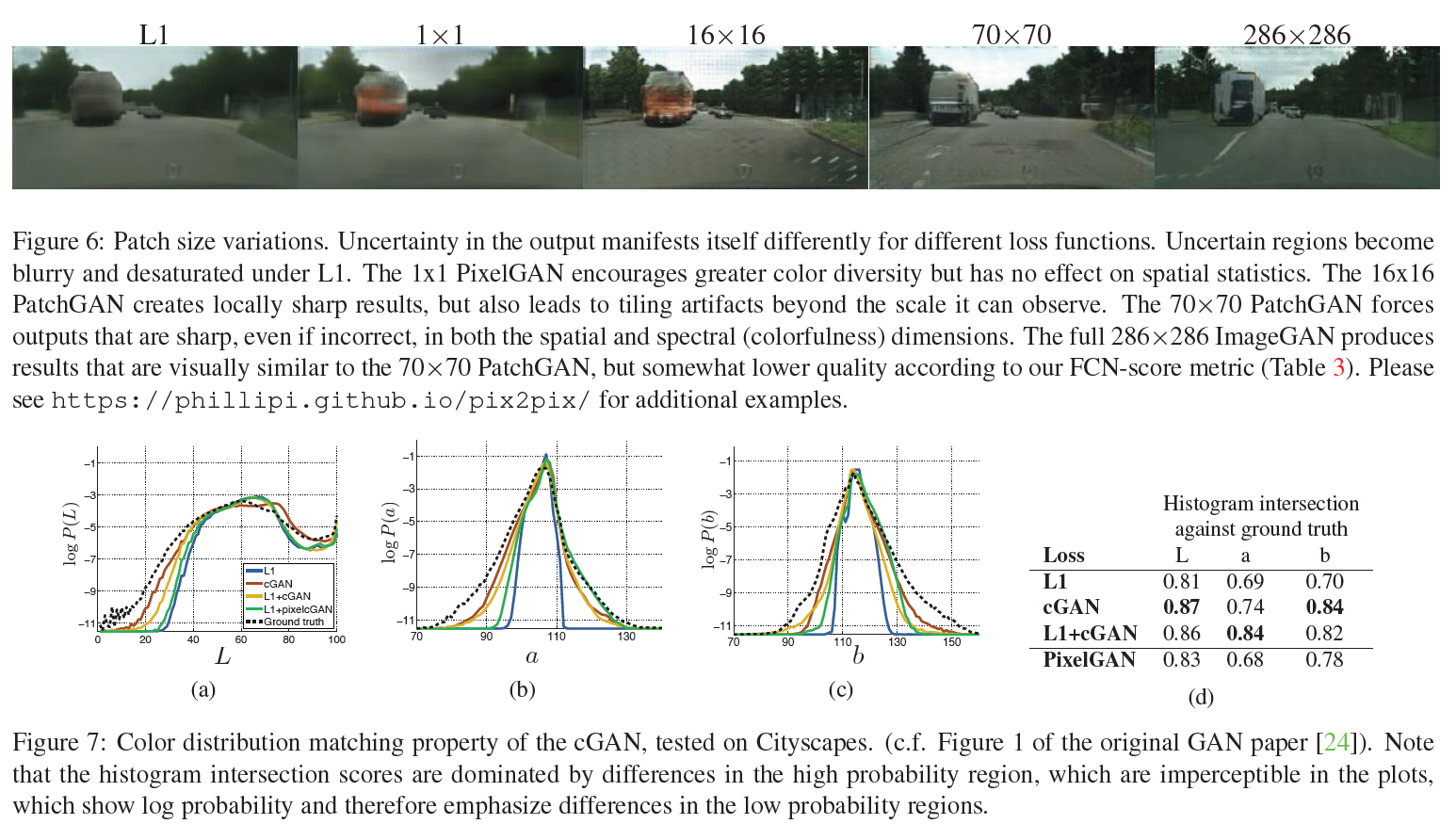
high-frequency 모델링을 위해, 집중할 부분(attention)을 local image patch 단위로만 제한하는 것으로 충분하다. 그래서, 우리는 D를 PatchGAN(일반 GAN인데 단지 Patch 단위로만 보는 것) 구조로 만들었다.
그래서 우리의 D는 $N \times N$개의 각 Patch별로 이 부분이 진짜인지 가짜인지를 판별한다.
실험 단계에서 우리는 $N$이 작아도 전체 이미지를 한번에 보는 것보다는 더 좋은 결과를 얻을 수 있음을 보였다. 이는 더 작은 PatchGAN은 더 적은 parameter를 가지고, 더 빠르며, 더 큰 이미지에 적용하는 데에서도 이점이 있음을 보여준다.
D가 이미지를 Markov random field처럼 보는 것이 효과적인 모델링 방법이므로, patch의 지름보다 더 먼 pixel들은 독립적이라고 보았다. 이러한 접근은 이미 연구된 바 있고, texture/style 모델에서 꽤 흔하며 적절한 가정이다. 따라서 PatchGAN은 texture/style loss면에서 충분히 이해가능한 모델이다.
최적화 및 추론(Optimization and inference)
일반적인 GAN 접근법을 따랐다. original GAN에서는 $log \ (1-D(x, G(x,z)))$를 최소화하는 대신 $log \ D(x, G(x,z))$를 최대화하는 것이 낫다고 했다.
그러나 우리는 D를 최적화하는 목적함수를 2로 나누어 D가 G보다 상대적으로 더 빠르게 학습되지 않도록 하였다.
또한 minibatch SGD와 Adam을 사용하였다($lr=0.0002, \beta_1 = 0.5, \beta_2 = 0.999$). 또한 batch size는 실험에 따라 1~10으로 조정하였다.
실험(Experiments)
conditional GAN의 보편성을 테스트하기 위해, 다양하게 진행하였다.
| Problem | Dataset |
|---|---|
| Semantic labels $\leftrightarrow$ photo | Cityspaces dataset |
| Architectural labels $\leftrightarrow$ photo | CMP Facades |
| Map $\leftrightarrow$ aerial photo | Google Maps |
| BW $\rightarrow$ color photos | ImageNet |
| Edges $\rightarrow$ photo | Natural Image manifold |
| Sketch $\rightarrow$ photo | human sketches |
| Day $\rightarrow$ night | ACM Transactions on Graphics |
| Thermal $\rightarrow$ color photos | Benchmark dataset and baseline |
| Photo with missing pixels $\rightarrow$ inpainted photo | Paris StreetView |
다른 네트워크보다 더 좋은 결과:

encoder-decoder보다 더 효과적인 U-Net:

Patch의 개수를 늘렸을 때의 선명도 상승:
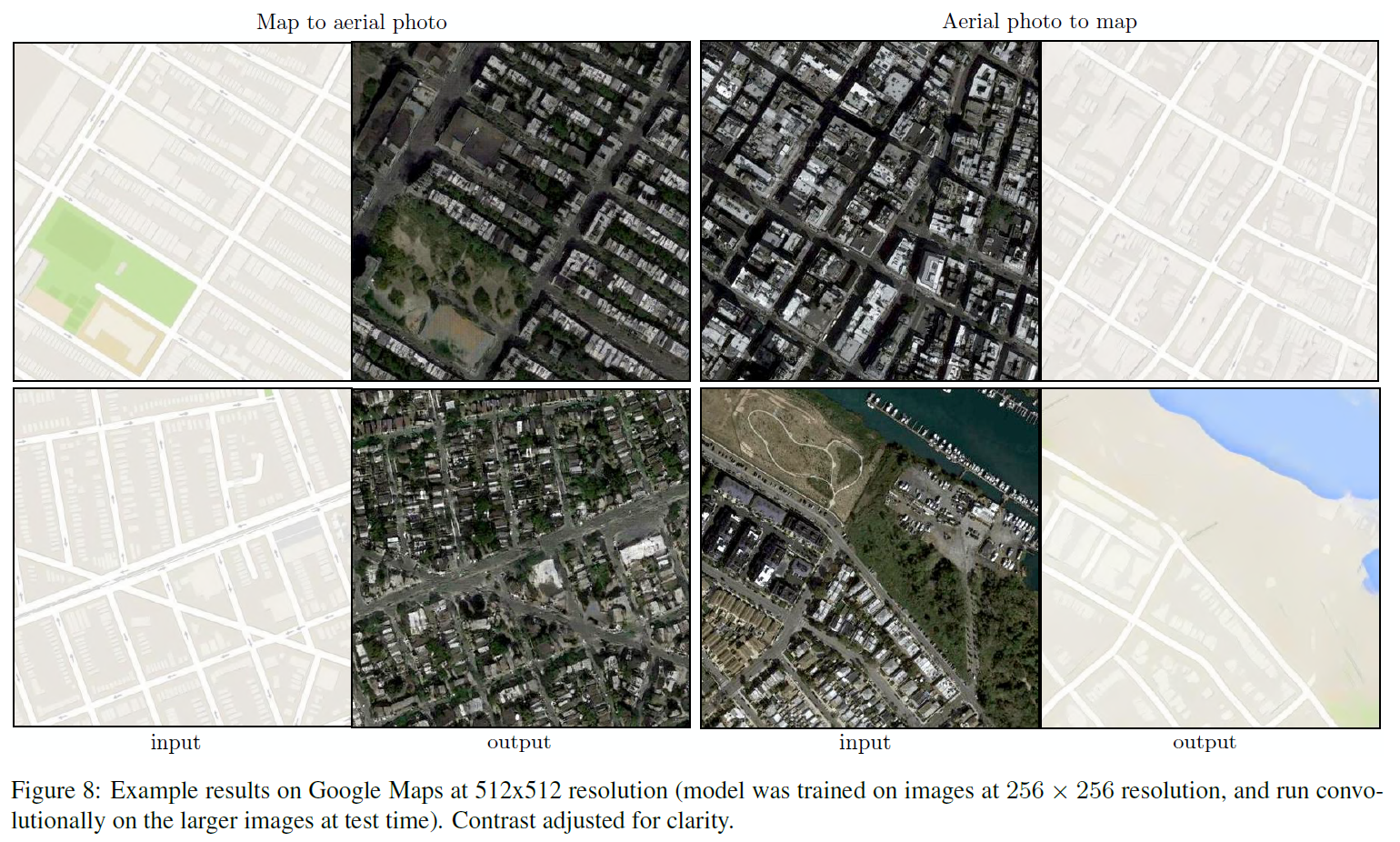
구글맵 사진과 도식화한 그림 간 변환 결과:
Colorization과 이미지 도식화:

등등 많은 결과가 논문에 나타나 있다.
사실 colorization 문제와 같은 것에서는 colorization에 특화된 네트워크가 더 좋은 결과를 내기는 한다.
그러나 이 Pix2Pix는 훨씬 더 넓은 범위의 문제를 커버할 수 있다는 점에서 의의가 있다.
더 많은 결과에 대해서는 여기를 참조하라.
결론(Conclusion)
이 논문에서는 image-to-image translation 문제에 대해, 특히 고도로 구조화된 그래픽 결과에 대해 conditional adversarial networks가 괜찮은 접근법이라는 것을 보여주었다. 이 네트워크는 문제와 데이터에 대한 loss를 학습함으로써 넓은 범위의 문제에 대해 적합함을 보여주었다.
Acknowledgments
매우 많다 ㅎㅎ
참고문헌(References)
논문 참조!
결론 이후에도 많은 실험 결과가 있으니 참조하시라. 매우 흥미로운 것들이 많다.




부록
Generator architectures
코드는 여기에 있다.
encoder는 C64-C128-C256-C512-C512-C512-C512-C512 구조이다(convolution layer).
decoder는 CD512-CD512-CD512-C512-C256-C128-C64 구조이다.
decoder의 마지막 레이어 이후 output 채널에 맞게 mapping되고(3, colorization에서는 2), Tanh 함수가 그 뒤를 따른다.
또한 encoder의 C64에서는 BatchNorm이 없다.
encoder의 모든 ReLU는 기울기 0.2의 Leaky ReLU이며, decoder는 그냥 ReLU이다.
U-Net decoder는 다음과 같이 생겼다. 앞서 언급했든 $i$와 $n-i$번째 레이어 사이에 skip-connection이 존재한다. 이는 decoder의 채널의 수를 변화시킨다.
CD512-CD1024-CD1024-C1024-C1024-C512-C256-C128
Discriminator architectures
$ 70 \times 70 $ discriminator의 구조는:
C64-C128-C256-C512
단 C64에는 BatchNorm이 적용되지 않는다.
마지막 레이어 이후 convolution을 통해 1차원으로 mapping하며 마지막에 sigmoid 함수가 적용된다.
0.2짜리 Leaky ReLU가 적용되었다.
다른 크기의(patch) D들은 조금씩 깊이가 다르다.
$ 1 \times 1 $ discriminator: C64-C128(convolution들은 $ 1 \times 1 $ spatial 필터를 사용)
$ 16 \times 16 $ discriminator: C64-C128
$ 286 \times 286 $ discriminator: C64-C128-C256-C512-C512-C512
학습 상세
- $ 256 \times 256 $ 이미지는 $ 286 \times 286 $ 크기로 resize되었다가 random cropping을 통해 다시 $ 256 \times 256 $가 되었다.
- 모든 네트워크는 scratch로부터 학습되었다.
- weights는 (0, 0.02) 가우시안 분포를 따르는 랜덤 초기값을 가진다.
- 데이터셋마다 조금씩 다른 기타 설정은 논문을 참조하자.

