Logistic Matrix Factorization 설명
02 Jun 2020 | Machine_Learning Recommendation System Paper_Review목차
본 글에서는 2014년에 Spotify에서 소개한 알고리즘인 Logistic Matrix Factorization에 대해 설명할 것이다. 먼저 논문 리뷰를 진행한 후, Implicit 라이브러리를 통해 학습하는 과정을 소개할 것이다. 논문 원본은 이곳에서 확인할 수 있다.
1. Logistic Matrix Factorization for Implicit Feedback Data 논문 리뷰
웹 상에서 얻을 수 있는 데이터는 대부분 암시적 피드백의 형태이기 때문에, 협업 필터링(Collaborative Filtering) 방법론에서도 이러한 암시적인 경우에 대응할 수 있는 알고리즘의 필요성이 대두되었다. 본 모델은 암시적 피드백에 적합한 새로운 확률론적 행렬 분해 기법인 LMF를 소개한다.
1.1. Problem Setup and Notation
암시적 피드백은 클릭, 페이지 뷰, 미디어 스트리밍 수 등을 예로 들 수 있는데, 모든 피드백은 non-negative의 값을 가지게 된다. 기본 기호는 아래와 같다.
| 기호 | 설명 |
|---|---|
| $U = (u_1, …, u_n)$ | n명의 User |
| $I = (i_1, …, i_n)$ | m개의 Item |
| $R = (r_{ui})_{n \times m}$ | User-Item 관측값 행렬 |
| $r_{ui}$ | User $u$가 Item $i$와 몇 번 상호작용 했는지(예: 구매횟수) |
1.2. Logistic MF
$f$를 잠재 벡터의 차원이라고 할 때, 관측값 행렬 $R$은 $X_{n \times f}, Y_{m \times f}$라는 2개의 행렬로 분해될 수 있다. 이 때 $X$의 행은 User의 잠재 벡터를 의미하고, $Y$의 행은 Item의 잠재 벡터를 의미한다. 이전의 방법에서는 weighted RMSE를 최소화하는 방법으로 행렬 분해를 진행했는데, 본 논문에서는 확률론적인 접근법을 시도하였다.
$l_{u, i}$를 User $u$가 Item $i$와 상호작용하기로 결정한 사건이라고 하자. 이 때 우리는 이러한 사건이 일어날 조건부 확률의 분포가 User와 Item의 잠재 벡터와 그에 상응하는 bias의 내적의 합이 parameter의 역할을 하는 Logistic Function에 따라서 결정되는 것으로 생각할 수 있다.
\[p(l_{ui} | x_u, y_i, \beta_i, \beta_j) = \frac{exp(x_u y^T_i + \beta_u + \beta_i)}{1 + exp(x_u y^T_i + \beta_u + \beta_i)}\]$\beta$항은 물론 bias를 나타내며, User와 Item 각각의 행동 분산을 의미하게 된다. $r_{ui}$가 0이 아닐 때 이를 positive feedback으로, 0일 때를 negative feedback으로 간주하자. 이 때 우리는 Confidence를 정의할 수 있는데, 이를 $c = \alpha r_{ur}$로 표현할 수 있다. 이 때 $\alpha$는 Hyperparameter이다. $\alpha$를 크게하면 할수록, Positive Feedback에 더욱 큰 가중치를 부여하게 된다. $c$는 Log를 활용하여 다음과 같이 표현할 수도 있다.
$R$의 모든 원소가 서로 독립적이라는 가정하게 Parameter인 $X, Y, \beta$가 주어졌을 때 관측값 행렬 $R$의 우도는 아래와 같이 표현할 수 있다.
\[\mathcal{L}(R|X,Y,\beta) = \prod_{u,i} p(l_{ui} | x_u, y_i, \beta_u, \beta_i)^{\alpha r_{ui}} ( 1 - p(l_{ui} | x_u, y_i, \beta_u, \beta_i))\]추가적으로, 우리는 학습 과정 상의 과적합을 막기 위해 User와 Item의 잠재 벡터에 0이 평균인 spherical Gaussian Prior를 부여한다.
\[p(X | \sigma^2) = \prod_u N(x_u | 0, \sigma^2_uI)\] \[p(Y | \sigma^2) = \prod_i N(y_i | 0, \sigma^2_iI)\]이제, Posterior에 Log를 취하고 상수항을 scaling parameter인 $\lambda$로 대체해주면 아래와 같은 식을 얻을 수 있다.
\[log p(R|X,Y,\beta) = \sigma_{u,i} \alpha r_{ui}(x_u y^T_i + \beta_u + \beta_i) - (1 + \alpha r_{ui}) log(1 + exp(x_u y^T_i + \beta_u + \beta_i)) - \frac{\lambda}{2} \Vert{x_u}\Vert^2 - \frac{\lambda}{2} \Vert{y_i}\Vert^2\]잠재벡터에 대한 0이 평균인 spherical Gaussian Prior는 단지 User와 Item 벡터에 대한 $l2$ 정규화를 의미한다. 이제 우리의 목표는 Log Posterior를 최대화하는 $X, Y, \beta$를 찾는 것이다.
\[argmax_{X,Y,\beta} log p (X,Y,\beta|R)\]위에서 제시된 목적 함수의 Local Maximum은 Alternating Gradient Ascent 과정을 거치면 찾을 수 있다. 각 Iteration에서 한 번은 User 벡터와 bias를 고정하고 Item 벡터에 대한 gradient를 업데이트하고, 그 다음에는 반대로 업데이트를 수행한다. User 벡터와 Bias의 편미분은 아래와 같다.
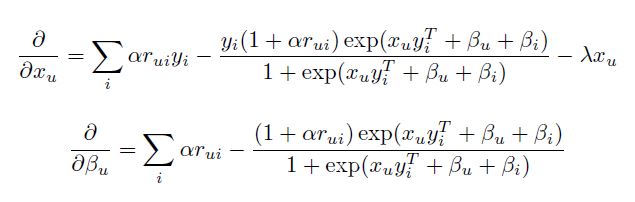
각 Iteration은 User와 Item의 수에 선형적인데, 만약 선형적 계산이 불가능한 상황이라면, 적은 수의 Negative Sample($r_{ui} = 0$)를 샘플링하고 이에 따라 $\alpha$를 감소시키는 방법을 쓸 수 있다.
이는 계산 시간을 굉장히 줄이면서도 충분히 최적점에 근접할 수 있는 장점을 지닌다. 또한 Adagrad 알고리즘을 활용할 경우 학습 시간을 획기적으로 줄이면서도 빠르게 수렴 지점에 도달할 수 있다. $x_u^t$를 Iteration $t$에서의 $x_u$의 값으로, $g_{x_u}^t$를 Iteration $t$에서의 $x_u$의 Gradient라고 할 때, $x_u$에 대하여 Iteration $t$에서 우리는 아래와 같이 Adagrad 알고리즘을 수행할 수 있다.
\[x_u^t = x_u^{t-1} + \frac{\gamma g_u^{t-1}}{\sqrt{\sum_{t`=1}^{t-1} g_u^{t^{`2}} }}\]1.3. Scaling Up
Alternating Gradient Descent의 각 Iteration은 모든 잠재 벡터에 대해 Gradient를 계산하고, 그 Gradient의 양의 방향으로 업데이트하는 과정을 포함하게 된다. 각 Gradient는 단일 User와 Item에 의존하는 함수의 집합의 합을 포함하게 된다. 이러한 합의 식은 병렬적으로 수행될 수 있고, MapReduce 프로그래밍 패러다임에 적합한 방법이다.
계산 향상을 위해 본 모델은 다른 잠재 요인 모델에서 사용된 것과 유사한 sharding 테크닉을 사용하였다. 먼저 $R$을 $K \times L$ 블록으로 나눈다. 그리고 $X$는 $K$개의 블록으로, $Y$는 $L$개의 블록으로 나눈다. 병렬 요인인 $K$와 $L$은 메모리에 맞게 설정할 수 있다. Map 단계에서 같은 블록에 있는 모든 $r_{ui}, x_u, y_i$를 같은 mapper에 할당한다. 각 $u, i$ 쌍에 대해 아래 식을 병렬적으로 수행한다.
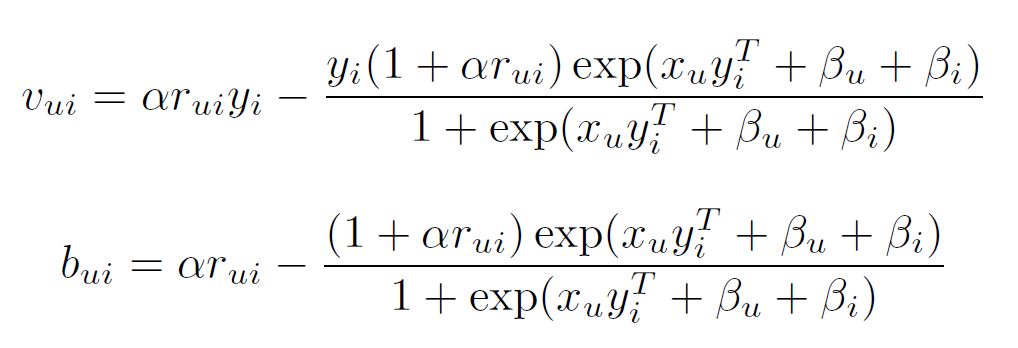
Reduce 단계에서는, 만약 $u$에 대한 반복을 수행하고 있다면, $u$를 key off하여 같은 User $u$에게 매핑되는 각 $v_{ui}, b_{ui}$가 같은 reducer에게 보내지도록 한다. 편미분이 계산되면 $x_u$와 $\beta_u$를 1.2. 절의 마지막 부분에 나온 식에 따라 업데이트 한다.
2. Implicit 라이브러리를 활용한 학습
Implicit 라이브러리는 이곳에서 확인할 수 있다. 본 장은 간략하게 메서드를 사용하는 방법에 대해서만 소개할 것이다. 학습의 자세한 부분에 대해서는 이전 글을 참조하길 바란다. 기본적인 틀은 유사하다.
LMF 알고리즘을 사용하기 위해서는 Sparse Matrix를 생성해주어야 한다. scipy 라이브러리를 통해 Sparse Matrix를 만든 후에는 간단하게 fit 메서드를 통해 적합해주면 된다.
현재로서는 GPU 학습은 지원하지 않는다. LMF를 학습할 때 조심해야 할 점은, 수렴 속도가 빨라 잠재 벡터의 수가 크고 learning_rate가 클 수록 반복 횟수가 일정 수준 이상일 때 잠재 벡터의 원소가 NaN이 되는 경우가 잦다는 것이다. 적절한 Hyper parameter 튜닝을 통해 이러한 경우를 조심해야 한다.
# 별 거 없다.
from implicit.lmf import LogisticMatrixFactorization
# 학습
lmf = LogisticMatrixFactorization(factors, learning_rate, regularization,
iterations, neg_prop, num_thread, random_state)
# 잠재 벡터 얻기
item_factors = lmf.item_factors()
user_factors = lmf.user_factors()
# 유사한 Item/User과 Score 리스트 얻기
# Input은 Integer
similar_items() = lmf.similar_items(itemid)
similar_users() = lfm.similar_users(userid)

