Graph Attention Networks (GAT) 설명
29 May 2021 | Machine_Learning Recommendation System Paper_Review목차
본 글에서는 2017년에 발표된 Graph Attention Networks라는 논문에 대한 Review를 진행할 것이다. 다방면에서 적용되는 Attention 개념을 Graph 구조의 데이터에 적용하는 초석을 마련한 논문이라고 할 수 있겠다. 자세한 내용은 논문 원본에서 확인하길 바라며 본 글에서는 핵심적인 부분만 다루도록 하겠다.
torch_geomectric을 이용하여 GAT를 사용하는 방법에 대해서 간단하게 Github에 올려두었으니 참고해도 좋을 것이다.
Graph Attention Networks 리뷰
1. Introduction
CNN은 image classification, semantic segmentation, machine translation 등 많은 분야에 성공적으로 적용되었지만, 이 때 데이터는 grid 구조로 표현되어 있어야 했다. 그런데 많은 분야의 데이터는 이렇게 grid 구조로 표현하기에 난감한 경우가 많다. 3D mesh, social network, telecommunication network, biological network 등이 그 예시라고 할 수 있다. 이러한 데이터는 Graph 구조로 표현할 수 있다.
굉장히 다양한 구조의 Graph를 다루기 위해 신경망을 확장하려는 시도는 지속되어 왔고, 초기 연구는 RNN으로 Graph 구조의 데이터를 다루고자 하였다. Graph Neural Network는 RNN의 일반화된 버전으로 소개되기 시작하였고 이후에 지속적으로 발전을 이어나갔다. 이후의 발전은 크게 2가지로 구분할 수 있을 것이다.
첫 번째는 Graph를 Spectral Representation으로 표현하는 것이다. Graph Laplacian의 eigen decomposition을 계산하는 Fourier domain으로 정의되는 합성곱 연산을 수행하는 것이 대표적인 방법이라고 할 수 있을 것인데, 이 연산을 통해 intense한 연산과 non-spatially localized한 filter를 만들어 낼 수 있다. 이러한 구조의 방법은 좀 더 세부적인 구조와 Feature의 특성을 반영하는데 특화되어 있지만 그 연산의 특성으로 인해, 새로운 구조의 Graph나 새로운 Node에 대해 대응하기 어려운 단점이 있다.
두 번째는 Non-spectral 혹은 Spatial Representaion으로 정의할 수 있겠다. 이는 합성곱을 Graph에 직접적으로 적용하고, spatially close한 이웃 그룹에 대해 연산을 수행하는 방법을 의미한다. 이러한 방법의 대표적인 예시가 바로 GraphSAGE이다. 이 알고리즘에 대해 자세히 알고 싶다면 이 글을 참조하면 될 것이다. 이러한 접근은 굉장히 scale이 큰 데이터에 대해 효과적인 접근으로 평가받고 있다.
위와 같은 최근 연구의 연장선에서, 본 논문에서는 Graph 구조의 데이터에 대해 Node Classification을 수행하기 위해 Attention 기반의 구조를 소개할 것이다. 연산은 효율적이며, 이웃들에 대해 각기 다른 weight을 지정함으로써 다른 degree(Node가 갖는 이웃의 수)를 갖는 Graph Node에 적용될 수 있다는 장점을 지니고 있다. 또한 이 모델은 Inductive Learning Problem에 직접적으로 적용될 수 있기 때문에 이전에 본 적이 없는 Graph에 대해서도 일반화할 수 있다는 큰 강점을 지닌다.
2. GAT architecture
2.1. Graph Attentional Layer
single Graph Attention Layer에 대해 설명할 것인데, 사실 이 layer가 본 논문에 소개된 GAT 구조에서 범용적으로 쓰인다. 본격적인 설명에 앞서 언제나 그렇듯 기호에 대해 잠시 정리하고 진행하겠다.
| 기호 | 설명 |
|---|---|
| $N$ | Node 수 |
| $F$ | Node의 Feature 수 |
| $F^{\prime}$ | Hidden Layer 길이 |
| $W$ | Trainable Parameter |
| $\vec{a}^{T}$ | Trainable Parameter |
아래와 같이 표현되는 Node Feature가 존재할 때,
\[\mathbf{h} = \{ \vec{h}_1, \vec{h}_2, ..., \vec{h}_N \}\]위 $\mathbf{h}$ 행렬은 Layer를 통과한 후 $\mathbf{h}^{\prime}$ 의 형상을 취하게 될 것이며, 그 shape은 $N, F^{\prime}$ 이 될 것이다.
$W = (F^{\prime}, F), \mathbf{a} = (2F^{\prime}, 1)$ 의 shape을 갖고 있을 때 Attention Coeffieicient는 아래와 같이 정의된다.
\[e_{ij} = a(\mathbf{W} \vec{h}_i, \mathbf{W} \vec{h}_j)\]위 식은 Node $i$ 에 대해 Node $j$ 의 Feature가 갖는 중요도를 의미한다. 이 때 $j$ 는 모든 Node를 의미하는 것은 아니고 $N_i$ 즉, Node $i$ 의 이웃에 대해서만 계산하게 된다. 최종적으로 softmax 함수를 통과하면 아래와 같은 Normalized Attention Score를 계산할 수 있다.
\[\alpha_{ij} = {softmax}_j (e_{ij}) = \frac{exp(e_{ij})}{\Sigma_{k \in N_i} exp(e_{ik})}\]이전 식에서 $a$ 로 표기되었던 Attention Mechanism은 single-layer feedforward 신경망으로, 아래와 같이 학습 가능한 파라미터와 LeakyRELU activation 함수로 정의할 수 있다.
\[\alpha_{ij} = \frac {exp (LeakyRELU ( \vec{a}^T [ \mathbf{W} \vec{h}_i \vert \mathbf{W} \vec{h}_j ] )) } { \Sigma_{k \in N_i} exp ( LeakyRELU ( \vec{a}^T [ \mathbf{W} \vec{h}_i \vert \mathbf{W} \vec{h}_k ] ) ) }\]이렇게 계산된 Attention Score는 아래와 같이 Node $i$의 이웃의 중요도를 결정하여 Input 데이터를 재정의하게 된다.
\[\vec{h}^{\prime}_i = \sigma( \Sigma_{j \in N_i} \alpha_{ij} \mathbf{W} \vec{h}_j )\]이를 그림으로 나타내면 아래와 같다.
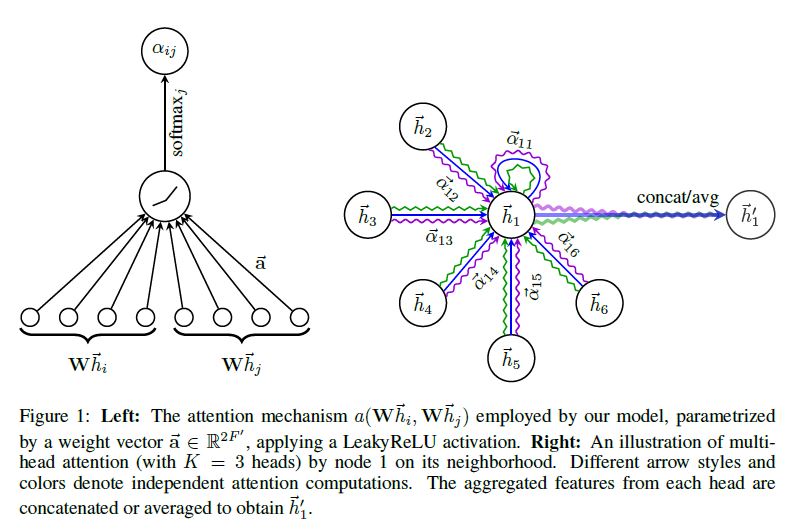
논문에서는 방금 설명한 Self Attention을 좀 더 안정화하기 위한 방법에 대해 상술하고 있는데 그 과정에 대해서는 아래 원문을 참조하길 바란다.

2.2 Comparison to related work
GCN과 달리 GAT는 같은 이웃 집단의 Node에 대해 다른 중요도를 배정하기 때문에 Model Capacity를 개선할 수 있으며 해석에 있어서도 도움을 주게 된다.
Attention Mechanism은 Graph의 모든 Edge에 공유되어 적용되기 때문에 전체 Graph에 대한 접근 없이도 학습이 진행될 수 있으며 이에 따라 Inductive Learning을 가능하게 한다.
GraphSAGE는 각 Node에 대해 고정된 수의 이웃을 추출하기 때문에 계산량을 일정하게 유지하게 되는데, 이는 추론을 행할 때 전체 이웃집단에 대해 접근할 수 없게 만드는 현상을 초래한다. 사실 본 논문에서는 LSTM Aggregator의 성능이 가장 좋았다고 기술하고 있는데, 이는 이웃 집단 내에서 각 이웃사이의 순서가 중요하다는 것을 암시하는 것과 다름이 없다. 만약 다른 Max Pooling Aggregator나 Mean Pooling Aggregator를 사용하였는데, 각 이웃 Node 사이의 순서 혹은 다른 개별적인 특징이 중요하다면, GraphSAGE는 이러한 부분까지는 커버하지 못하는 단점을 지니게 된다. 본 논문에서 제시하는 GAT는 이러한 한계에서 자유로우며 이웃 전체에 대해 접근하면서도 효율적으로 학습을 진행할 수 있다는 장점을 지닌다.
3. Evaluation
(중략)
3.4. Results
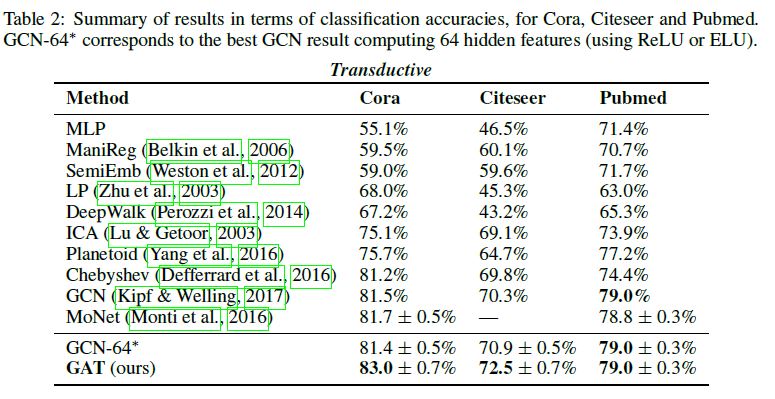
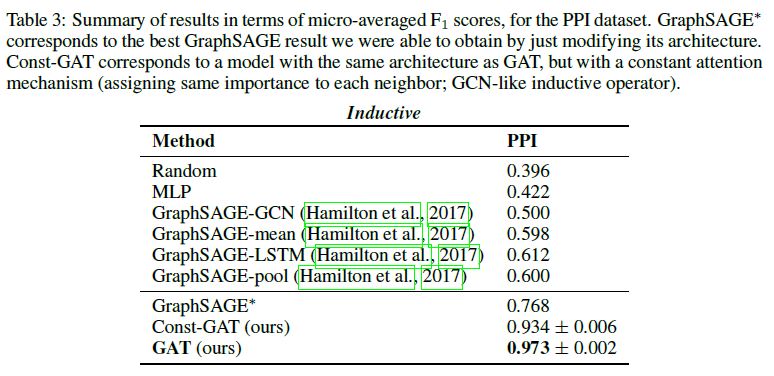
실험 결과에 대해서는 논문 원본을 참조하길 바란다.
4. Conclusion

본 논문에서는 Graph Neural Network (GAT)를 제시하였는데, 이 알고리즘은 masked self-attentional layer를 활용하여 Graph 구조의 데이터에 적용할 수 있는 새로운 Convolution-style의 신경망이다.
효율적인 연산과, 각기 다른 이웃 Node에 다른 중요도를 부과할 수 있다는 장점을 지니고 있으며 전체 Graph에 대한 접근 없이도 학습이 가능하기 때문에 Inductive Learning이 가능한 구조이다.

