Graph Isomorphism Network (GIN) 설명
05 Jun 2021 | Machine_Learning Recommendation System Paper_Review목차
- Graph Isomorphism Networks 리뷰
- References
본 글에서는 2018년에 발표된 How Powerful are Graph Neural Networks라는 논문에 대한 Review를 진행할 것이다. 본 논문에서는 Graph Neural Network에서 거의 필수적으로 진행되는 Aggregation 과정에서의 문제점을 지적하고 이를 해결할 방법으로 Graph Isomorphism Network를 제시하고 있다.
앞으로 상세히 설명할 Aggregation 과정에서의 문제는 필자 역시 GraphSAGE 기반 알고리즘을 사용하면서 경험적으로 느껴왔던 부분이기에 본 논문에서 제시하고 있는 방법론과 연구 결과는 더욱 의미있게 다가왔다. 논의를 전개하면서 근간으로 사용되는 수학적 이론들은 깊이를 요구하지만, 전반적으로 이야기를 이끌어가는 핵심 아이디어는 굉장히 간단하다. 결국 Graph의 구조적인 특성을 GNN이 더 잘 표현하도록 만들고 싶다는 이야기인 것이다.
참고로 논문에서 직접적으로 언급하고 있는 GraphSAGE에 대해 궁금하다면, 이 글을 참조하면 좋을 것이다.
torch_geomectric을 이용하여 GIN를 사용하는 방법에 대해서 간단하게 Github에 올려두었으니 참고해도 좋을 것이다.
또한 Reddit Data를 이용하여 GIN을 적용하는 예시는 이 글을 참조하면 좋고, Pyspark와 Tensorflow를 이용하여 Bipartite Graph 구조에서 GIN을 적용하는 사례에 대해 참고하고 싶다면 이 곳을 확인해 보아도 좋다.
Graph Isomorphism Networks 리뷰
1. Introduction
GNN은 Neighborhood Aggregation 혹은 Message Passing이라는 반복적인 과정을 수행하여 각 Node의 새로운 Feature 벡터를 형성하기 위해 이웃 Node의 이웃을 통합하게 된다. 이러한 통합이 과정이 k번 수행되고 나면, 그 Node는 변형된 Feature 벡터로 표현될 것이고, 이는 그 Node의 k-hop Neighborhood 안에 존재하는 구조적인 정보를 포착하게 된다.
GNN이 괄목할 만한 성과를 거두어왔던 것은 사실이지만, GNN의 새로운 디자인은 대부분 경험적 직관, 휴리스틱, 혹은 실험에 기반한 것으로 GNN의 특징과 한계점에 대한 이론적인 연구가 부족했던 것을 사실이다. 또한 GNN의 Representional Capacity에 대한 이전의 연구도 제한적이었다.
따라서 본 논문에서는 GNN의 Representational Power에 대해 분석하는 이론적인 프레임워크를 제시할 것이다. 이 프레임워크는 GNN과 Weisfeiler-Lehman Graph Isomorphism Test 사이의 유사성에 기반하여 만들어졌는데, 이 WL Test는 여러 종류의 Graph를 구별할 수 있는 효과적인 테스트 방법으로 알려져 있다.
GNN과 비슷하게, WL Test도 Node가 주어졌을 때, 이 Node의 이웃들의 Feature 벡터를 통합하여 Node Feature 벡터를 반복적으로 업데이트한다. WL Test의 경우 다른 Node 이웃들을 다른 Feature 벡터로 매핑하는 Injective Aggregation Update의 존재로 인해 강력한 효과를 지니게 된다.
이 말이 무엇을 의미하는지 잘 생각해 보아야 하므로 예시를 들어 보겠다. (물론 논문 본문에서 잘 설명하고 있다.)
아래와 같은 Node와 Feature 벡터가 주어졌다고 해보자.
| Node | Feature Vector |
|---|---|
| 알라딘 서점 | [1, 0, 0.5] |
| 스타벅스 커피 | [0, 1, 0.5] |
| 이디야 커피 | [0.5, 0.5, 0.5] |
이 때 알라딘 서점과 스타벅스 커피는 사람 A의 이웃 Node이고, 이디야 커피는 사람 B의 이웃 Node라고 생각해보자. 그리고 사람 A와 사람 B의 Feature 벡터를 얻기 위해 GraphSAGE에서 제시한 Mean Aggregation 과정을 진행한다고 해보자.
그렇다면 사람 A의 이웃 Node의 Feature 벡터는 [0.5, 0.5, 0.5]가 될 것이고, 사람 B의 이웃 Node의 Feature 벡터 또한 [0.5, 0.5, 0.5]가 될 것이다. 물론 위 예시에 대해 애초에 Feature 값이 이들을 표현하기에 불충분하다고 생각할 수도 있지만, 충분히 실제 데이터 상에서 나타날 수 있는 예시일 것이다. 어쨌든 위 결과에 따르면 사람 A와 사람 B의 이웃 Feature 벡터는 똑같은 형상을 하게 될 것이고, 이는 학습에 있어서 데이터 소실 혹은 왜곡이라는 문제로 귀결되게 될 것이다.
본 논문에서는 GNN의 Aggregation Scheme이 굉장히 Expressive하고 Injective Function을 모델링할 수 있다면 GNN 또한 WL Test 처럼 굉장히 강력한 Disciminative Power를 지니게 될 것이라고 이야기 하고 있다.
수학적으로 위 인사이트를 공식화하기 위해, 본 논문의 Framework는 먼저 Node가 주어졌을 때, 이 Node의 이웃들의 Feature 벡터를 Multiset, 즉 repeating elements가 존재할 수 있는 집합으로 표현할 것이다. 그러면 GNN에 있는 Neighbor Aggregation이 Aggregation Function over the multiset으로 표현될 수 있을 것이다. 따라서 강력한 Representational Power를 가지기 위해서는 GNN은 다른 multiset을 다른 representation으로 표현할 수 있어야 한다.
본 논문에서는 몇몇 multiset function의 변형 버전과 그들의 discriminative power, 즉 aggregation function이 다른 multiset들을 얼마나 잘 구별할 수 있는지를 이론적으로 분석하였다. 더 disciminative 할 수록, GNN 속에 내재되어 있는 Representational Power는 더 강력할 것이다.
본 논문의 핵심적인 결과는 아래와 같다.
1) GNN은 Graph 구조를 판별하는데에 있어 WL Test 만큼이나 효과적이다.
2) 위 문장이 성립하기 위해서는 Neighbor Aggregation이나 Graph Readout Function에 관하여 조건들이 필요한데, 본 논문에서는 이를 제시하였다.
3) 본 논문에서는 GCN이나 GraphSAGE는 구분할 수 없는 Graph 구조에 대해 언급하고, GNN 기반의 모델들이 포착할 수 있는 Graph 구조들에 대해 정확하게 분석하였다.
4) 본 논문에서는 GIN이라고 부르는 간단한 신경망 구조를 고안하였고, 이 알고리즘이 WL Test 만큼이나 discriminative/representational power를 갖고 있음을 증명하였다.
2. Preliminaries
이 Section은 GNN의 기본에 관한 것이므로 간단히만 짚고 넘어가도록 하겠다. 자세한 내용은 논문 원본을 참고하면 좋을 것이다.
Graph Neural Networks
GNN은 Graph 구조와 Node Feature $X_v$ 를 활용하여 Node에 대한 Representation 벡터 $h_v$ 혹은 전체 Graph $h_G$ 를 학습하는 것을 목적으로 한다. 현대의 GNN은 이웃의 표현을 통합하여 Head Node의 Feature를 업데이트하기 위해 Neighborhood Aggregation이란 방법을 사용한다. GNN의 k번째 layer는 아래와 같이 표현할 수 있을 것이다.
$h_v^{(k)}$ 는 Node $v$ 의 $k$ 번째 반복 혹은 layer의 Feature 벡터를 의미하게 된다. 위에서 표기한 Aggregate 및 Combine 함수는 정말로 중요한 부분이다. 이를 어떻게 정의하느냐에 따라 GNN의 디자인과 효과는 굉장히 상이할 수 있다. GraphSAGE에서는 Aggregate 부분을 아래와 같이 정의하고 있다.
\[a_v^{k} = MAX( ReLU(W \cdot h_u^{k-1}), \forall u \in \mathcal{N} (v) )\]Combine 부분은 아래와 같이 concatenation 방식으로 정의된다.
\[W [h_v^{k-1}, a_v^k]\]GCN에서는 Aggregate 및 Combine 방식을 아래와 같이 통합하여 element-wise mean pooling을 사용하였다.
\[h_v^k = ReLU( W \cdot MEAN \{ h_u^{k-1}, \forall u \in \mathcal{N} (v) \cup \{ v \} \} )\]Node Classification의 경우 최종 Layer의 Representation이 예측을 위해 사용되며, Graph Classification의 경우 Readout 함수가 아래와 같이 Node Feature들을 통합하게 된다.
\[h_G = Readout ( \{ h_v^K \vert v \in G \} )\]Weisfeiler-Lehman Test
Graph Isomorphism (동형 이성) 문제는 2개의 Graph가 위상적으로 동일한지 판단하는 문제를 의미한다. 이는 굉장히 큰 문제인데, 왜냐하면 아직까지 polynomial-time 알고리즘을 알려지지 않았기 때문이다. 몇몇 극단적인 예시를 제외하고는 WL Test의 경우 Graph의 broad class를 구별하는 효과적인 테스트로 평가받고 있다.
WL Test는 반복적으로 Node의 Label과 이웃을 통합한 후, 이렇게 통합된 label 혹은 이웃을 unique한 새로운 Label로 Hash한다. 이 알고리즘은 만약 일정 수준의 반복 이후 2개의 Graph에 존재하는 Node들의 Label이 달라지게 되면 2개의 Graph는 non-isomorphic 하다고 판단한다.
3. Theoretical Frameworks: Overview
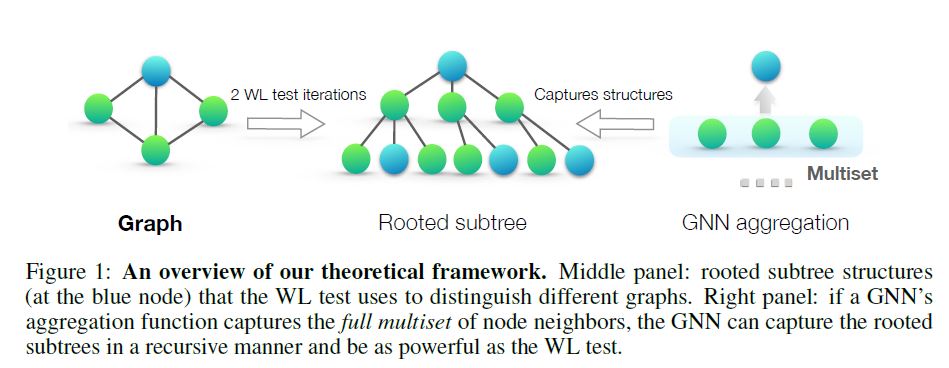
GNN은 반복적으로 Node의 Feature 벡터를 업데이트하여 Network 구조와 다른 이웃 Node의 Feature들을 포착한다. 본 논문에서는 Node Input Feature는 countable universe에서 왔다고 가정할 것이다. 유한한 수의 Graph에 대해 어떠한 고정된 모델 하의 깊은 Layer에 있는 Node Feature 벡터 또한 countable universe에서 왔다. 단순하게 기호를 표현하기 위해, 본 논문에서는 각 Feature 벡터에 대해 고유한 Label을 $a, b, c …$ 와 같이 붙여줄 것이다. 그리고 나서 이들의 이웃 Node의 Feature 벡터로 multiset을 형성할 것이다. 이 때 다른 Node라 하더라도 같은 Feature 벡터를 가질 수 있으므로 같은 element도 여러 번 등장할 수 있다.
Multiset의 정의를 다시 짚고 넘어가기 위해 아래 논문 원본을 참조하면 좋을 것이다.
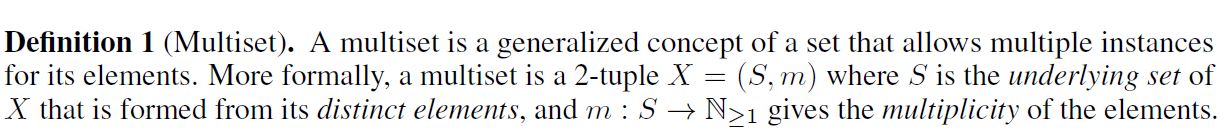
GNN의 Representational Power를 연구하기 위해, 본 논문에서는 GNN의 2개의 Node를 Embedding 공간 상에서 같은 위치에 매핑할 때를 분석하였다. 직관적으로 이러한 경우가 발생하기 위해서는, 각 Node가 존재하는 subtree 구조가 동일해야 할 것이다. 이 때 subtree 구조는 Node의 이웃에 의해 재귀적으로 정의되므로 이제 논의 주제는, 과연 GNN이 2개의 이웃 집합(Neighborhood)을 같은 Embedding 혹은 Representation으로 매핑할 것인가 하는 문제로 생각해 볼 수 있다.
Maximally Powerful GNN이라면 2개의 다른 이웃 집합(혹은 multisets of feature 벡터)을 같은 Representation에 매핑하지 않을 것이다. 이 때의 Aggregation Scheme은 반드시 Injective해야 한다. 따라서 본 논문에서는 GNN의 Aggregation Scheme을 이 신경망이 표현하는 multiset에 대한 함수의 class로 추상화하고, 이 신경망이 injective multiset function을 표현할 수 있는지 분석할 것이다.
다음 Section에서는 이러한 추론을 바탕으로 가장 강력한 GNN을 소개할 것이다. Section 5에서는 유명한 GNN 변형 버전들에 대해 이야기하고, 이들의 Aggregation Scheme이 내재적으로 injective하지 않고, 그렇기 때문에 덜 powerful하며 Graph의 흥미로운 특징들을 잘 담아내지 못한다는 것을 증명할 것이다.
4. Building Powerful Graph Neural Networks
우리는 Isomorphic Graph는 같은 Representation을 갖고, Non-isomorphic Graph는 다른 Representation을 갖길 원한다. 본 분석에서는 WL Test라는 다소 약한 기준을 통해 GNN의 Representational Capacity를 분석할 것이다.

모든 lemma와 theorem에 대한 증명은 본 논문의 부록에서 찾을 수 있다. 어쨌든, 어떠한 aggregation 기반의 GNN은 다른 Graph를 구별하는 데에 있어서는 WL Test만큼이나 강력해질 수 있다. 다음에 이어질 자연스러운 질문은 정말로 WL Test만큼이나 강력한 GNN이 존재할 것인가 하는 것이다. 아래 Theorem3에 따르면 답은 ‘그렇다’이다. 만약 Neighbor Aggregation 및 Graph-level readout 함수가 injective하다면, 이에 따른 GNN은 WL Test만큼이나 강력할 것이다.

위 이론은 중요하다. 이 부분에 대한 증명은 부록에서 찾아볼 수 있다.
좀 더 Simple하게 바꿔보자. 중요한 것은 Injective Multiset Function은 아래와 같이 표현된다는 것이다.
\[\varphi ( \Sigma_{x \in S} f(x) )\]이 때 $\varphi, f$ 는 어떤 비선형 함수이고, $\Sigma$ 부분은 multiset에 대한 합 연산을 의미한다. 예시를 들면 쉽다. 아래 그림을 보면, One-hot 인코딩으로 이루어진 3개의 Node Feature 벡터가 합 연산으로 통합되었을 때, 모든 정보를 보존하고 있는 것을 알 수 있다.
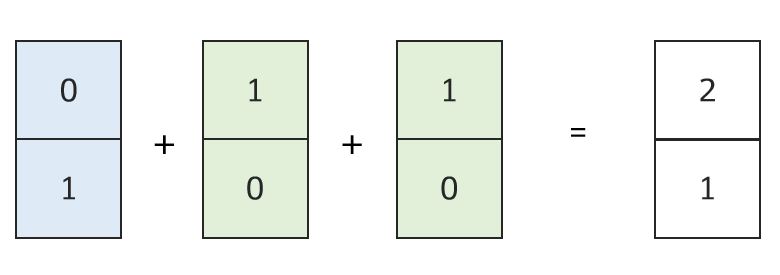
이 때 위 Feature 벡터들이 One-hot 인코딩된 형태가 아니라 연속형 변수들로 구성되어 있다면 이들을 한 번 더 처리하기 위해 다른 과정이 필요할 것이다. 이 다른 과정을 본 논문에서는 MLP로 처리하고 있고, 이에 대해서는 아래 4.1에서 확인할 수 있다.
유한한 수의 집합에 대해, Injectiveness는 함수가 Input의 distinctness를 잘 보존하는지를 특징화한다. 셀 수 없는 집합에 대해서는, 만약 Node Feature가 연속형 변수라면 추가적인 조건이 더 필요하다. 더 나아가 학습된 Feature가 함수의 이미지 속에서 어떻게 가깝게 존재하는지 파악해보면 좋을 것이다. 이 부분에 대해서는 추후 연구로 남겨두고, 본 논문에서는 유한한 수의 집합에 대해서만 다루도록 하겠다.

다른 Graph를 구별하는 것을 넘어서 Graph의 구조적 유사성을 포착하는 GNN의 중요한 특징에 대해 논의해보는 것도 중요하다. WL Test에 존재한는 Node Feature 벡터들은 본질적으로 One-Hot 인코딩되었기 때문에 subtree 사이의 유사성을 잡아내지 못한다. Theorem3을 만족하는 GNN은 반대로 subtree를 저차원 공간에 embed하는 법에 대해 학습함으로써 WL Test를 일반화 할 수 있다. 이 점이 GNN으로 하여금 다른 구조를 판별할 뿐만 아니라 유사한 Graph 구조를 유사한 Embedding에 매핑하고 Graph 구조 간의 의존성을 포착하도록 해준다.
4.1. Graph Isomorphism Network (GIN)
Maximally Powerful GNN에 대한 조건을 수립한 이후, 본 논문에서는 Graph Isomorphism Network: GIN이라는 간단한 구조를 고안하였고, 이 알고리즘은 Theorem3을 만족한다. 이 모델은 WL Test를 일반화하며 따라서 현존하는 GNN 중에서 가장 강한 disciminative power를 지니고 있다.
Neighbor Aggregation을 위한 Injective Multiset Function을 모델링하기 위해, 본 논문에서는 Universal Multiset Function을 신경망과 함께 파라미터화 하는 Deep Multisets 이론을 제안한다. 아래 lemma가 aggregator를 더하는 것이 multiset에 대해 injective & universal한 함수를 표현한다는 것을 말해준다.
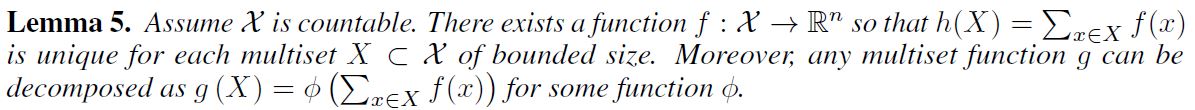
Deep Multiset과 Sets 사이의 중요한 구별점이라고 한다면, Mean Aggregator와 같은 특정한 유명 Injective Set Function의 경우 Injective Multiset Function은 되지 못한다는 것이다. lemma5의 Universal Multiset Function를 building block으로 모델링하기 위한 메커니즘으로 Node와 그 이웃의 multiset에 대한 Universal Function을 표현하는 Aggregation Scheme은 Theorem3에 있는 Injectiveness 조건을 만족한다고 생각할 수 있다. 아래 corollary는 이러한 여러 Aggregation Scheme 사이에 존재하는 간결하고 구체적인 formulation을 제공한다.
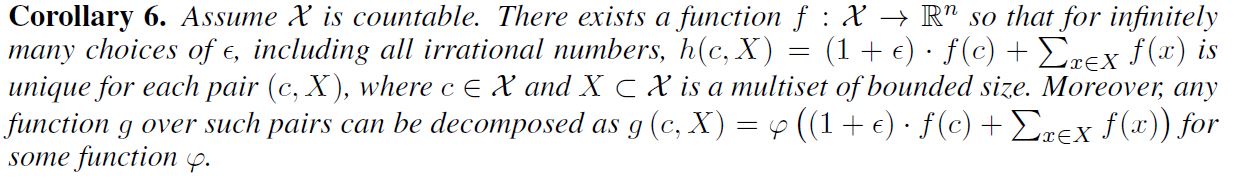
Universal Approximation Theorem 덕분에 위에서 제시되고 있는 함수 $f, \varphi$ 를 모델링하기 위해서 본 논문에서는 MLP를 사용할 것이다. 실제로 MLP는 여러 함수들의 Composition을 표현할 수 있기 때문에 본 논문에서는 $f^{k+1} \circ \varphi^k$ 를 하나의 MLP로 모델링할 것이다.
잠시 Universal Approximation Theorem에 대해서 짚고 넘어가자. 원본 논문은 이 곳에서 확인할 수 있다.
핵심 내용은 간단하다. 충분히 큰 Hidden Dimensionality와 적절한 비선형 함수를 갖는 1-hidden-layer MLP는 일정 수준의 정확도로 어떠한 연속형 함수도 근사할 수 있다는 것이 본 이론의 내용이다.
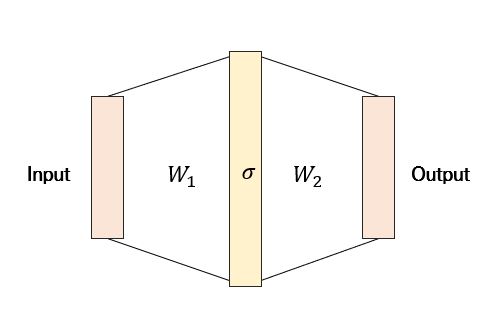
최초의 반복에서 만약 Input Feature가 One-hot 인코딩이면 그들의 합 또한 injective할 것이기 때문에 합 연산 이전에 MLP가 필요하지는 않다. 물론 One-hot 인코딩 되어 있지 않거나 연속형 변수가 중간에 끼어 있다면 MLP가 필요할 것이다. $\epsilon$ 의 경우 학습 가능한 파라미터 혹은 고정된 스칼라로 둘 수 있다. 최종적으로 GIN은 Node Representation을 아래와 같이 업데이트하게 될 것이다.
효과적인 GNN은 많이 존재하지만 GIN은 굉장히 간단하면서도 굉장히 효과적인 GNN의 대표적인 예라고 할 수 있다.
4.2. Graph-level Readout of GIN
Graph-level의 readout에서 중요한 측면은, 반복 횟수가 증가할 수록 subtree 구조에 따른 Node Representation이 더욱 정제되고 global해진다는 것이다. 충분한 반복이 지속되면 훌륭한 discriminative power를 얻을 수 있지만 때로는 반복을 적정 수준에서 멈췄을 때의 feature가 일반화 측면에서 더 나은 모습을 보이기도 한다.
사실 위 문제는 GNN에서 고질적으로 지적되는 Over-smoothing 문제라고 해석할 수 있다. 이 문제는 사용하는 이웃의 수가 많아지고, GNN의 Layer 깊이가 점점 더 깊어질 수록 Node 임베딩이 서로서로 비슷해지는 경향을 보이는 현상을 말한다.이 문제에 대해서는 추후에 다른 글에서 더욱 상세하게 다루도록 하겠다.
본 논문에서는 모든 구조적인 정보를 활용하기 위해 모델에 존재하는 모든 깊이 및 반복에서 생성된 정보를 활용하였다. 이를 위해서 본 논문에서는 Jumping Knowledge Network와 비슷한 구조를 차용하였다. 본 논문에서는 GIN에 존재하는 모든 반복/Layer 속에서 Readout 방식을 아래와 같이 변형하였다는 차이가 있다. 참고로 앞서 언급한 논문은 이 곳에서 전문을 확인할 수 있다.
\[h_G = CONCAT ( READOUT ( \{ h_v^k \vert v \in G \} ) \vert k=0, 1, ..., K )\]5. Less Powerful but still interesting GNNs
GNN의 여러 변형 버전들의 경우 WL Test에 비해 단순한 Graph에도 쉽게 오류를 범하고 성능 측면에서도 다소 아쉬운 모습을 보이긴 하지만, GCN에서의 Mean Aggregator의 경우도 Node Classification Task 등에서는 굉장히 잘 작동한다. 이 부분에 대해 더욱 자세히 이해하기 위해 Graph를 학습하는 데에 있어 다른 GNN의 변형 버전들이 어떻게 Graph에 대해 학습하고 정보를 습득하는지 정확히 알아볼 것이다.
5.1. 1-Layer Perceptrons are not sufficient
현존하는 많은 GNN 구조는 1-layer MLP를 사용하고 있다. 그렇다면 이 구조는 Graph 학습에 있어 충분할까? 아래 lemma는 그렇지 않은 경우가 존재한다는 것을 알려준다.
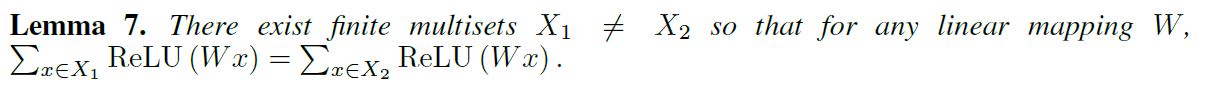
위 내용을 증명할 핵심 아이디어는, 1-layer 퍼셉트론은 linear mapping과 유사하게 작동하기 때문에 GNN layer들이 이웃 Feature들을 단순히 합산하는 수준으로 퇴보할 수 있다는 것이다. 물론 이 때의 이야기는 bias term이 존재하지 않을 때를 가정한 것이고, 만약 bias term이 존재한다면 충분히 큰 output 차원이 전제될 때, 1-layer 퍼셉트론도 다른 multiset을 구분할 가능성이 꽤 높아진다.
그럼에도 불구하고 MLP를 이용한 모델에 비해 1-layer 퍼셉트론은 multiset 함수에 대한 Universal Approximator라고 할 수 없다. 결과적으로 1-layer 퍼셉트론을 이용한 GNN은 어느 수준까지는 다른 Graph를 다른 위치에 Embed 할 수 있지만, 충분히 그 특징을 잡아내지는 못할 수도 있다.
5.2. Structures that confuse mean and max-pooling
만약 $h(X) = \Sigma_{x \in X} f(x)$ 에 있는 합 연산을 GCN이나 GraphSAGE에 있는 Mean 혹은 Max-pooling으로 대체한다면 어떤 일이 발생할까?
Mean/Max-pooling Aggregator는 permutation invariant하기 때문에 여전히 잘 정의된 multiset 함수이지만 결정적으로 이들은 injective하지 않다.
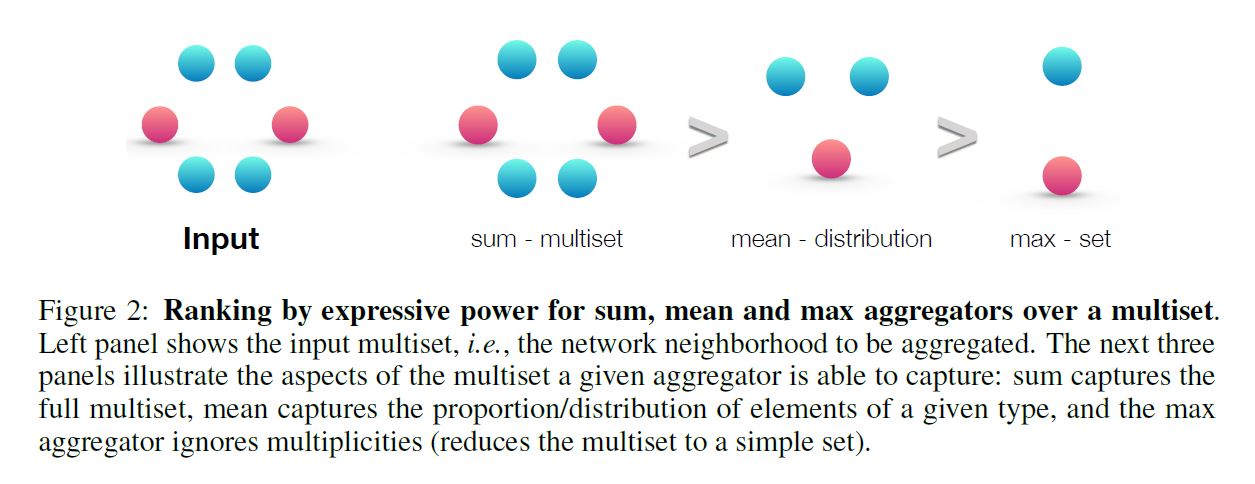
위 그림을 보자. 3가지 방법이 존재할 때 이들의 표현력을 기준으로 순위를 매기면 위와 같은 결과를 얻을 수 있다. 이 때 같은 색의 Node는 같은 Node Feature를 갖는 것을 전제로 한다. 왜 이런 결과가 나오는지 아래 그림을 통해 알아보자.

a, b, c에 있는 Graph들은 모두 다른 구조를 갖고 있지만, 위와 같이 Mean/Max-pooling Aggregator는 다른 구조임을 인지하지 못한다. 이러한 사례가 바로 구조적인 정보를 포착하지 못하는 대표적인 사례가 된다. 반대로 Sum Aggregator는 차이를 인지할 수 있다.
(후략)
6. Other Related Work
(생략)
7. Experiments
본 논문에서는 GIN과 GNN의 여러 변형 버전들의 성능에 대해 평가해보았다. 이 실험의 목적은 모델이 단지 Input Node Feature에 의존하지 않고 Network 구조를 학습하도록 하는 것이다. 본 실험에서 사용한 bioinformatics graph에 대해서는 Node는 Categorical Input Feature를 가지며, Social Network 데이터에서는 feature가 없다. Reddit 데이터셋에서는 모든 feature를 같게 만들어 사실상 의미 없도록 만들었으며, 다른 데이터셋에 대해서는 node degree를 One-hot 인코딩으로 추가하여 Feature를 생성하였다.
참고로 GIN-0은 $\epsilon$ 을 0으로 고정한 모델을 의미한다. 모든 설정에서 Input Layer를 포함하여 총 5개의 layer가 사용되었고 모든 MLP는 2개의 layer를 갖게 하였다. Batch Normalization은 모든 Hidden Layer에 적용되었다. Adam Optimizer가 사용되었고 최초의 Learning Rate은 0.01이고, 50 Epoch이 진행될 때마다 0.5씩 Learning Rate에 decay를 적용하였다.
bioinformatics graph에서는 16, 32의 hidden unit을, social graph에서는 64개의 hidden unit을 사용하였다. Batch Size는 32와 128 중에 선택하였고 Dropout Rate은 0 혹은 0.5를 선택하였다. 그리고 이 Dropout layer는 Dense Layer 이후에 적용되었다.
Training Set Performance
높은 Representational Power를 갖고 있는 모델일수록 Training Set에서의 정확도도 높을 것이다. 아래 그림을 보면 그 결과가 나와 있다.
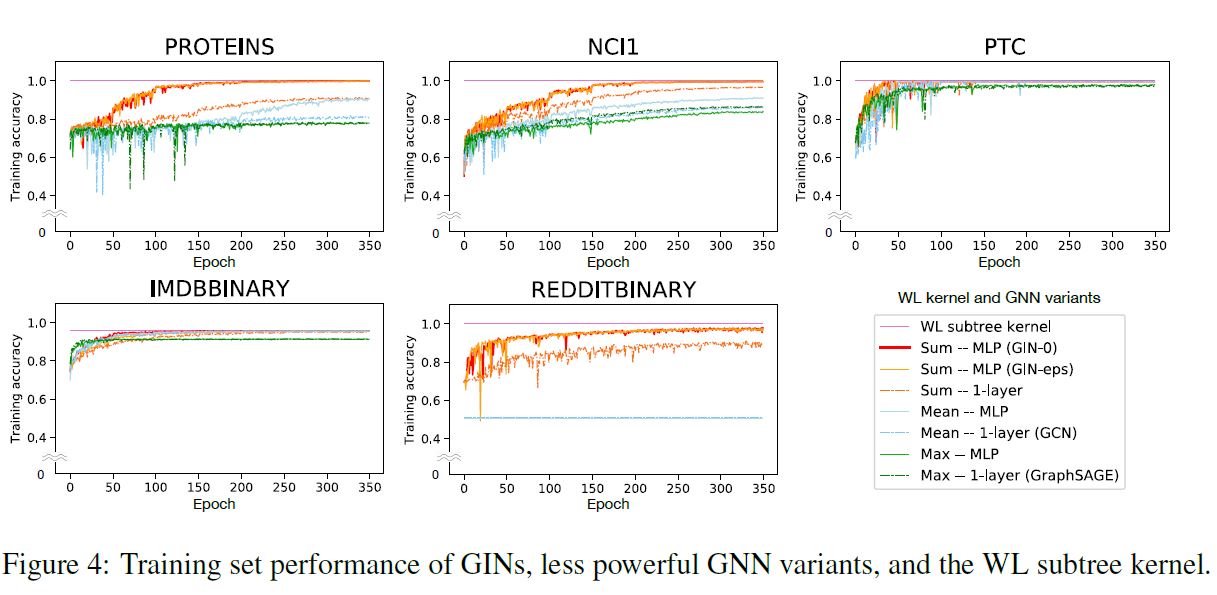
결과를 보면 GIN-$\epsilon$ 과 GIN-0이 가장 좋은 성과를 보임을 알 수 있다. 본 실험의 결과에 따르면 $\epsilon$ 을 명시적으로 학습하는 것에 있어서 큰 효과는 나타나지 않았다. GNN의 다른 변형 버전들은 상대적으로 낮은 성과를 보였다. 또한 MLP layer가 1-layer 퍼셉트론보다 더 나은 성능을 기록하였다. 그리고 Mean/Max-pooling Aggregator 보다는 Sum Aggregator가 더 나은 결과를 보여주었다.
모든 결과에서 GNN은 WL Test를 넘어서지는 못했는데, 이는 매우 당연한 것이 GNN은 WL Test에 비해 낮은 Discriminative Power를 갖고 있기 때문이다.
Test Set Performance
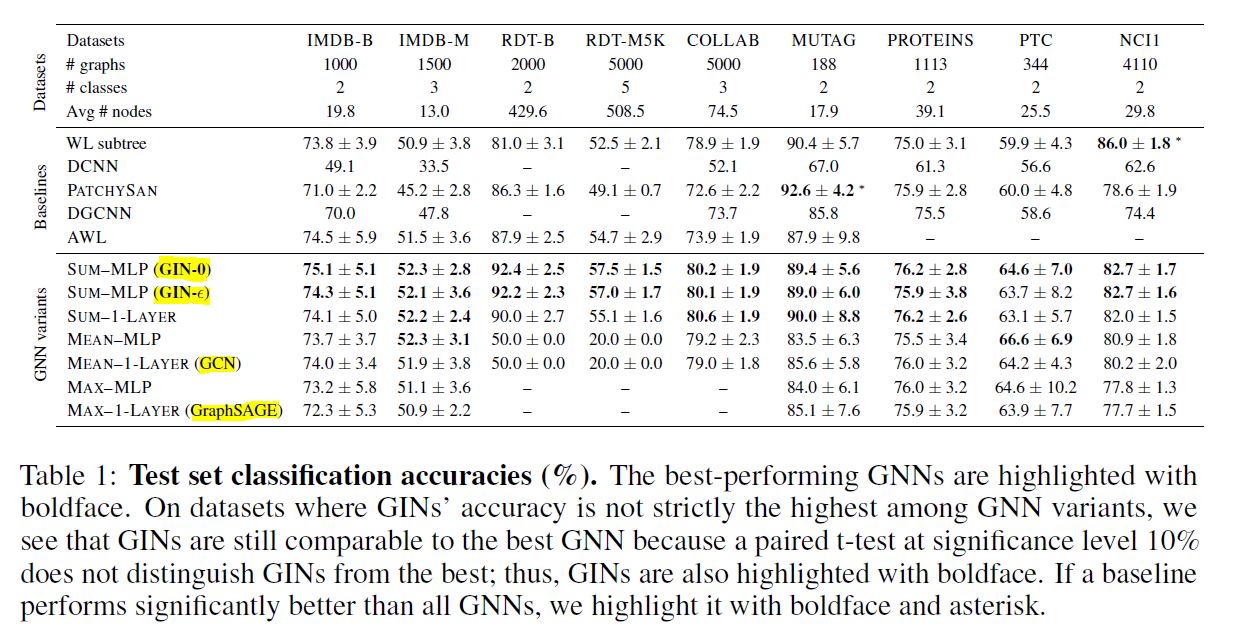
테스트 셋에서의 결과를 보면 꼭 GIN이 최고의 결과를 보여준 것은 아님을 알 수 있다. 본 논문에서는 분류 성능으로 GNN의 Expressive Power를 가늠해보는 정도라고 이야기하고 있는데, 이 설명은 조금은 아쉽긴 하다. 개인적으로는 추가적인 설명이 더 있었으면 좋았을 것이라는 생각이 든다.
어쨌든 이번 결과에서 보면 GIN-0이 눈에 띄는 성과를 지속적으로 보이고 있음을 알 수 있다. 물론 이는 데이터셋의 특성에 기인한 것일 수 있고, 만약 Head Node의 특성이 풀고자 하는 문제에서 가장 중요한 특성이라면 $\epsilon$ 을 활용하는 것이 더 나은 선택이 될 수 있을 것이다. 실제로 필자가 현실 데이터에서 본 알고리즘을 활용해본 경험에 의하면, User-Item 사이의 Link Prediction을 풀어내는 문제에서는 $\epsilon$ 을 학습하는 것이 분류 성능 자체에 있어서는 더욱 도움이 되었다. (다만 이것이 전반적인 Graph와 Node의 특성을 더욱 잘 학습했다는 결론으로 직접적으로 귀결되는 것은 아니다.) 어쨌든 GIN-0이 전반적으로 더 나은 성과를 보인 것은 흥미로운 부분이다.
8. Conclusion
본 논문에서는 GNN의 Expressive Power에 대한 추론을 위한 이론적인 근간을 마련하였고, 여러 유명한 GNN의 변형 버전들의 Representational Capacity에 대한 엄격한 한계를 증명하였다. 또한 Neighborhood Aggregation Framework 하에서의 가장 powerful한 GNN 구조를 고안하였다.
미래 연구로 흥미로운 방향이 있다면, 지금껏 전제로 삼아온 Neighborhood Aggregation 혹은 Message Passing을 넘어서면서 Graph를 학습하는 powerful한 구조를 만들어 보는 것을 생각해 볼 수 있다. 이를 위해서는 GNN의 최적화 뿐만 아니라 이 네트워크의 일반화 특성을 이해하고 더 개선하는 방향으로 연구가 실행되어야 할 것이다.

