IGMC (Inductive Graph-based Matrix Completion) 설명
26 Aug 2021 | Machine_Learning Recommendation System Paper_Review목차
이번 글에서는 IGMC란 알고리즘에 대해 다뤄보겠다. 상세한 내용을 원하면 논문 원본을 참고하길 바라며, 본 글에서는 핵심적인 부분에 대해 요약 정리하도록 할 것이다.
Github에 관련 코드 또한 정리해서 업데이트할 예정이다.
Inductive Matrix Completion based on Graph Neural Networks 설명
1. Background
행렬 분해 알고리즘의 기본에 대해 알고 싶다면 이 글을 참조하길 바란다. Graph Neural Networks을 이용하여 Matrix Completion 알고리즘을 구축한 대표적인 예는 GC-MC가 될 것이다. 이에 대해 알고 싶다면 이 글을 참고하면 좋다. GC-MC는 Bipartite Graph에 직접적으로 GNN을 적용하여 user와 item의 잠재 벡터를 추출하였다. 이전의 대부분의 연구와 마찬가지로 GC-MC 또한 Transductive한 모델로, 학습 셋에서 사용하지 않은 unseen nodes에 대한 대응이 불가능하다는 단점을 지니고 있었다. GraphSAGE, PinSAGE 등 여러 알고리즘에서 Inductive한 방법론을 제시하기는 했지만 이들 방법론을 적용하기 위해서는 node의 feature가 풍부해야 한다.
node feature에 크게 의존하지 않으면서도 Inductive한 학습/예측 환경으로 앞서 기술한 문제점들을 상당 부분 해결한 모델이 IGMC: Inductive Graph-based Matrix Completion이다.
2. IGMC 알고리즘 설명
일반적으로 통용되는 방식으로 기호를 정의하고 시작하겠다.
| 기호 | 설명 |
|---|---|
| $\mathbf{G}$ | undirected bipartite graph |
| $\mathbf{R}$ | rating matrix |
| $ u, v $ | 각각 user, item node |
| $ r = \mathbf{R}_{u, v} $ | user $u$ 가 item $v$ 에 부여한 평점 |
| $ \mathcal{N}_r (u)$ | user $u$가 평점 $r$ 을 준 $v$ 의 집합, 즉 edge type $r$ 에 대한 $u$ 의 이웃 집합 |
IGMC의 핵심 아이디어는 user $u$ 와 item $i$ 에 관련이 있는 local subgraph를 추출하여 이를 학습에 활용한다는 점이다.
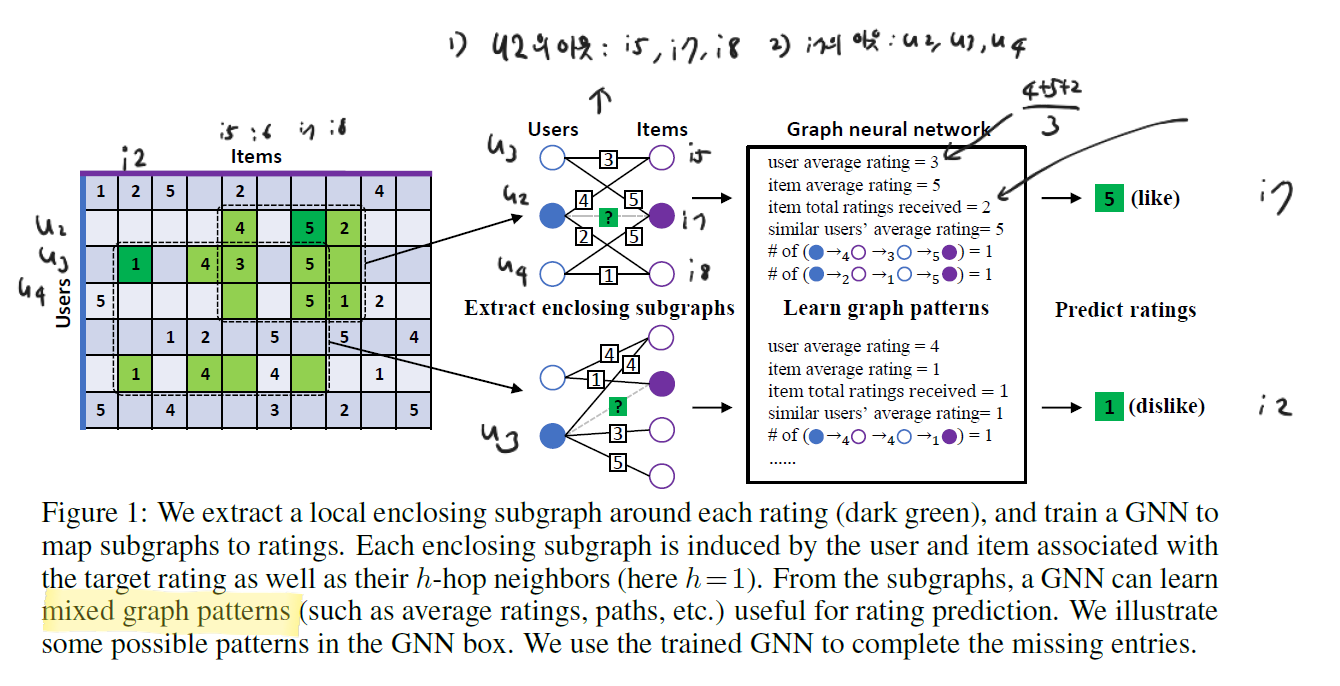
위 그림을 보면 이해가 될 것이다. 진한 초록색 5점의 예시를 보면, $u_2$ 가 $i_7$ 에게 5점을 부여한 것을 알 수 있다. 그렇다면 이 두 node에 대한 1-hop enclosing subgraph는 $u_2$ 의 1-hop neighbor인 [ $i_5, i_7, i_8$ ], 그리고 $i_7$ 의 1-hop neighbor인 [ $u_2, u_3, u_4$ ]로 구성되는 것이다. 물론 최종적으로 학습/예측을 할 때는 Target Rating인 5점은 masking될 것이다.
subgraph를 추출하는 BFS 과정은 아래 표에 나와있다.

다음으로는 node labeling 과정이 필요하다. 여기에서의 label은 y값이 아니고, 각 node의 임시 ID를 의미한다. subgraph를 추출하였으면 이 node를 구분할 id가 필요한데, IGMC의 경우 global graph를 참조하는 경우는 없고 오직 subgraph만을 이용하여 학습/예측을 수행하기 때문에 기존의 id 방식을 그대로 따를 필요가 없다. IGMC의 구조에 맞게 바꿔보자.
| 구분 | user id | item id |
|---|---|---|
| target | 0 | 1 |
| 1-hop | 2 | 3 |
| 2-hop | 4 | 5 |
| h-hop | 2h | 2h+1 |
위와 같이 subgraph 내에서의 node id를 다시 붙여주면 (node labeling) 각각의 node들은 역할에 맞게 구분된다. 위 label을 통해 0과 1을 추출하여 target node를 구분할 수 있고, 홀수/짝수 구분을 통해 user/item을 구분할 수 있으며, $h$ 의 값을 통해 어떤 계층(h-hop)에 속하는지도 파악할 수 있다. 이러한 node label을 One-hot 인코딩하여 초기 node feature로 활용할 수 있다.
다음 단계는 GNN을 통해 학습을 수행하는 것이다. IGMC의 특징이라면 GC-MC를 비롯한 여러 알고리즘과 달리 node-level GNN이 아니라 graph-level GNN을 사용한다는 것인데, 논문에서는 이 부분에 대해 장점을 크게 어필하고 단점을 끝에 살짝 언급한 수준에 그쳤는데 상황에 따라 단점이 더 클 수도 있다는 개인적인 의견을 덧붙인다.
GNN의 기본 구조를 message passing과 pooling(or aggregation)이라고 정의할 때, message passing은 Relational Graph Convolution Operator: R-GCN 포맷을 사용하였다.
활성화 함수로는 tanh를 사용하게 된다. 1번째 $\Sigma$ 는 각 Rating 별로 따로 파라미터를 둔다는 것을 의미하며, 그 내부에서는 일반적인 GCN이 적용된다. 다만 이 때 이웃 집합의 크기를 나타내는 $\mathcal{N}_r^i$ 가 global graph가 아닌 local subgraph에서 계산된 것이기 때문에 효율적으로 연산이 가능하다는 점은 기억해둘 필요가 있다. 이렇게 쭉 진행해서 $L$ 번째 Layer까지 값을 얻었으면 아래와 같이 최종 hideen representation을 얻는다.
\[\mathbf{h}_i = concat(x_i^1, x_i^2, ..., x_i^L)\]위와 같은 방식을 적용하면, jumping network의 효과도 있을 것으로 보인다. 이렇게 user, item에 대해 각각의 hidden 벡터를 구한 뒤 이를 다시 하나의 벡터로 결합하면 (sub) graph representation을 얻을 수 있다. 이렇게 graph 표현 벡터를 얻는 것을 graph-level GNN이라고 한다.
\[\mathbf{g} = concat(\mathbf{h}_u, \mathbf{h}_v)\]위와 같은 pooling 과정은 간단하지만 실제로 적용하였을 때 우수한 성과를 내는 것이 실험으로 증명되었다고 한다. MLP를 적용해서 최종적으로 rating 예측 값을 얻을 수 있다.
\[\hat{r} = \mathbf{w}^T \sigma (\mathbf{W} \mathbf{g})\]활성화 함수는 ReLU를 사용하였다.
3. Model Training
Mean Squared Error를 Loss Function으로 사용하였다.
\[\mathcal{L} = \frac{1}{\vert \{ (u, v) \vert \Omega_{u, v} = 1 \} \vert} \Sigma_{(u, v): \Omega_{u, v} = 1} (R_{u, v} - \hat{R}_{u, v})^2\]$\Omega$ 부분은 관측된 edge에 대해서만 Loss를 계산하겠다는 뜻을 담고 있다.
R-GCN layer에 AAR: Adjacent Ratin Regularization이라는 기법이 적용되었다. 이 부분은 사실 GC-MC에서도 간과하고 있었던 부분으로, 평점의 정도(magnitude)를 고려하기 위해서 도입되었다. R-GCN layer를 보면 사실 평점 4점이 평점 1점에 비해 5점에 더 가깝다를 나타내는 그 어떠한 장치도 마련되어 있지 않다. 이를 위해서 아래와 같은 ARR Regulaizer가 적용되었다.
이 때 $\Vert \Vert_F$ 는 행렬의 frobenius norm을 의미한다. 이 부분에 대해서는 이 글의 가장 마지막 슬라이드를 참고해도 좋다. 결과적으로 이 규제항을 적용하면 $\mathbf{W}_5$ 는 $\mathbf{W}_4$ 와 비슷해지는 효과가 나타날 것이다.
최종 Loss 함수는 아래와 같다.
\[\mathcal{L}_{final} = \mathcal{L}_{MSE} + \lambda \mathcal{L}_{ARR}\]모델 구현은 pytorch_geometric에 기반하여 이루어졌고, 저자의 코드는 이 곳에서 참고할 수 있다. 상세한 세팅은 논문을 직접 참고하길 바란다.
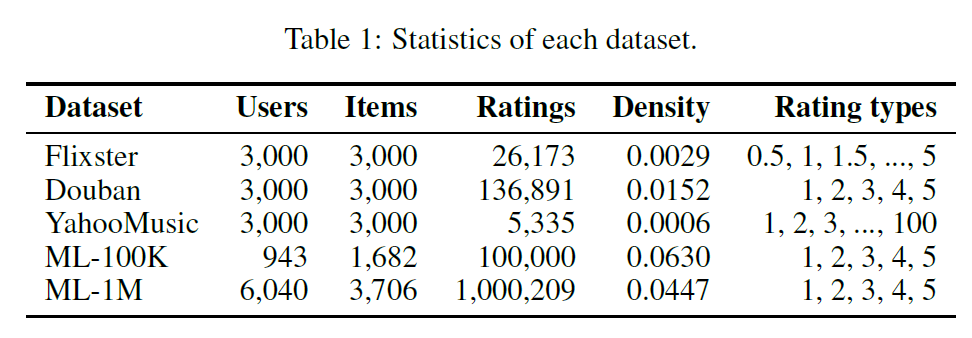
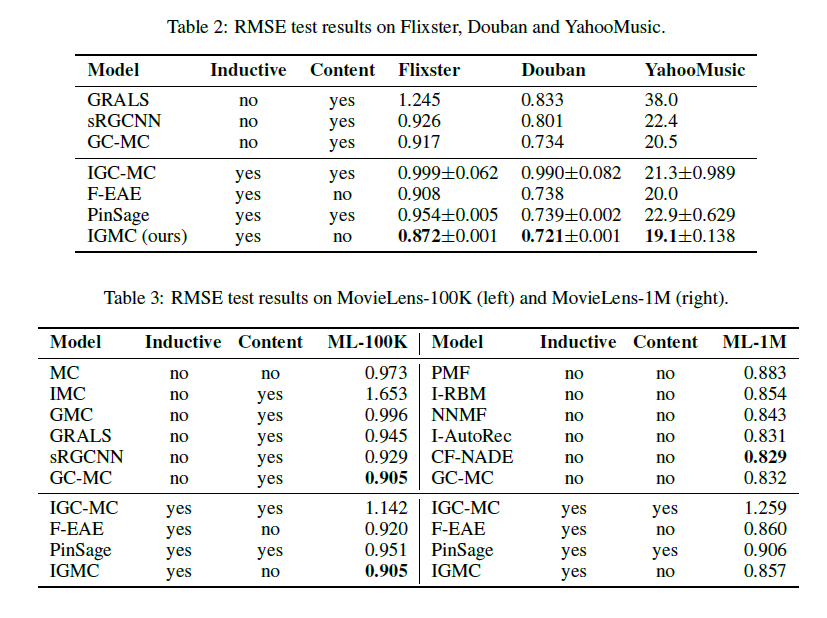
여러 데이터셋에 대한 실험 결과는 아래와 같다. IGMC가 대체적으로 좋은 성과를 보이는 것을 확인할 수 있다. 하나 기억해야 할 부분은 F-EAE 알고리즘을 제외하면 다른 비교 모델들은 각 데이터의 node feature를 활용한 반면, IGMC는 앞서 기술한 것처럼, node의 feature에 의존하지 않았다는 점이 흥미롭다. 즉 그러한 feature 없이도 설정에 따라 충분한 성능을 확보할 수 있다는 의미이다.
4. 인사이트 종합
IGMC의 핵심 인사이트는 아래와 같이 정리할 수 있겠다.
1) node feature와 같은 side information 없이도 충분한 성능을 확보할 수 있음
2) local graph pattern은 user-item 관계를 파악하기에 충분함
3) long-range dependency는 추천 시스템을 구상할 때 크게 중요하지 않은 경우가 많음
4) sparse한 데이터에서도 충분히 성능을 발휘할 수 있음
5) node feature에 의존하지 않기 때문에 transfer learning에도 효과적으로 활용할 수 있음
6) graph-level prediction을 통해 더욱 효과적인 학습/예측을 수행할 수 있음
7) 1-hop neighbors 까지만 추출해도 충분한 성능을 확보할 수 있음
4번에 대해서는 논문의 5.3 section에 설명이 되어있다.
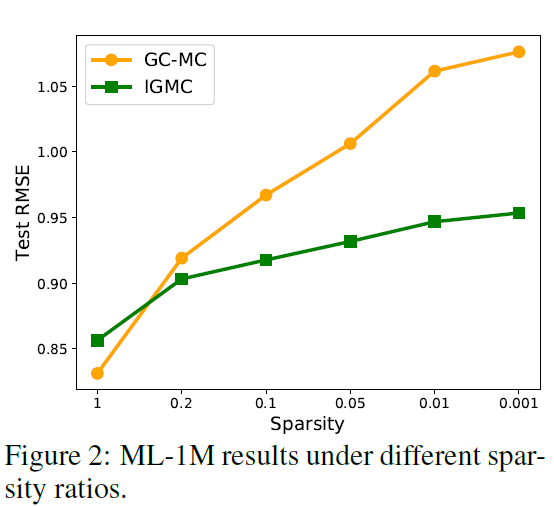
위 그림과 같이 GC-MC에 비해 sparsity가 강화되는 환경에서 RMSE의 증가폭이 완만한 것을 확인할 수 있다. 이는 Transductive한 Matrix Completion 방법론은 밀집도가 높은 user-item interaction에 더욱 의존한다는 것을 의미한다.
5번의 경우 논문의 5.4 section에 설명되어 있다. IGMC는 node feature가 부재한 상황에서도 Inductive한 학습 환경을 구축할 수 있다는 특징을 가지는데, 이를 이용하여 실제로 실험을 수행해본 결과 transfer learning에도 효과적임이 입증되었다.
6번의 경우 아래 그림을 바탕으로 설명하겠다.
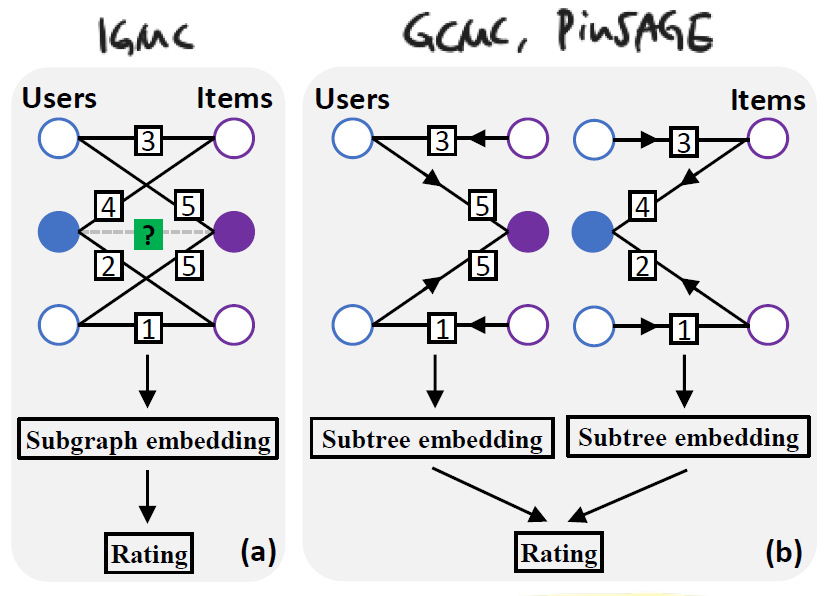
좌측이 IGMC의 예시인데, $\mathbf{g}$ 라는 (sub) graph representation을 생성한 뒤 한 번 더 MLP를 거쳐 최종 예측 값을 반환하기 때문에 graph-level prediction의 형태를 띠고 있다. 반면 우측의 경우 user, item 각각의 representation을 형성 한 후 내적 기반의 연산을 통해 예측 값을 반환하게 된다.
논문에서는 이렇게 각 node의 subtree embedding을 독립적으로 구하는 것이 각 tree의 상호작용과 상관성을 포착하기 어렵다는 문제점을 지닌다고 지적한다. 즉, convolution range를 늘린다 하더라도 (h-hop 에서 h를 늘린다 하더라도) target node와 별 상관 없는, 먼 거리에 있는 node들이 subgraph에 포함되어 over-smoothing 문제를 야기할 수 있다는 것이다. 이 부분은 합당한 지적이며 IGMC는 이러한 단점을 보완하여 더욱 높은 성능의 결과를 보여줌으로써 해결 방안을 제시했다고 볼 수 있다.
다만 논문에서도 언급하였듯이 IGMC의 graph-level 학습 세팅은 시간이 더욱 오래 걸린다는 단점을 지닌다. 비록 추출된 subgraph의 최대 edge 수를 특정 값 = $K$ 로 제한하는 방법을 통해 이를 어느 정도 보완할 수는 있겠지만 구조적으로 node-level prediction이 갖는 시간적 이점을 압도하기는 어려운 것이 사실이다.
이 부분에 있어서는 본인이 마주한 task에 따라 장단점을 따져야 할 것으로 보이며, 성능과 속도 사이의 적절한 완급 조절이 필요할 것으로 보인다. 만약 IGMC와 같은 graph-level prediction으로는 충분한 속도를 확보하기 어렵다면 user, item 각각의 representation을 구한 뒤 scoring을 수행하는 node-level prediction의 구조를 일부 차용하여 IGMC를 변형하는 방법 또한 실질적으로 고려해볼 수 있을 것이다.
7번의 경우 필자도 실제 여러 GNN 모델을 적용해보면서 느낀 바인데, 1-hop neighbors로도 괜찮은 성과를 보이는 경우가 많았다.
추가적으로 IGMC의 한계를 짚고 넘어가자면, IGMC는 Inductive한 방법론이기에 unseen nodes에 대해 대응이 가능하지만 다른 수 많은 GNN 모델과 마찬가지로 아예 아무 interaction이 없으면 접근에 있어 어려움이 있다.
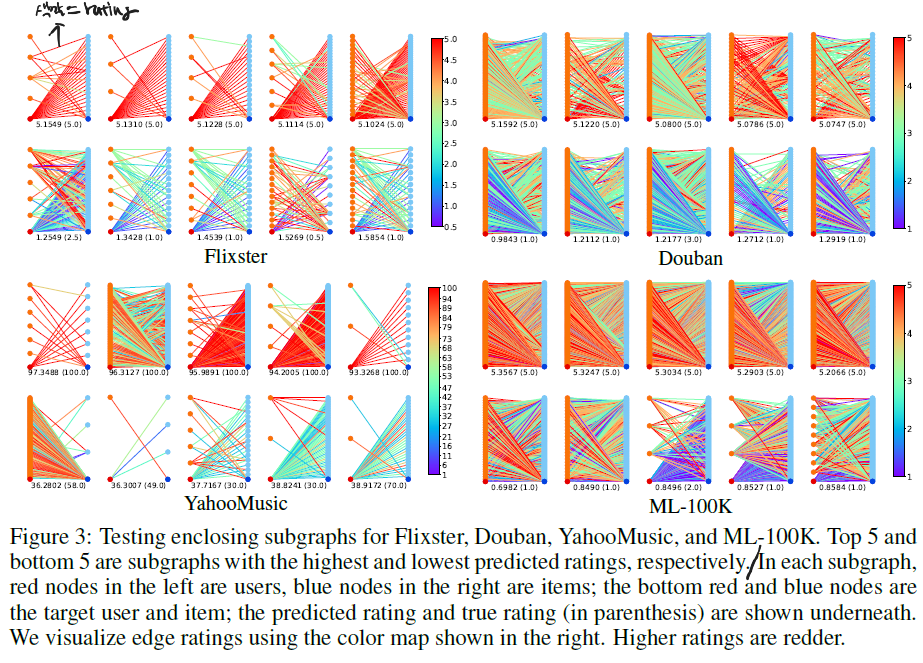
Appendix: high-score & low-score subgraph의 다른 패턴