목차

• Scalable Inception Graph Neural Networks 설명
  • 1. Background
  • 2. Architecture
  • 3. Experiments & Insights

이번 글에서는 SIGN이란 알고리즘에 대해 다뤄보겠다. 상세한 내용은 논문 원본을 참고하길 바라며, 본 글에서는 핵심적인 부분에 대해 요약 정리하도록 할 것이다. Twitter Research의 Gitub에서 코드를 참고할 수도 있다.

torch_geomectric을 이용하여 SIGN를 사용하는 방법에 대해서 간단하게 Github에 정리하도록 할 것이다.

Scalable Inception Graph Neural Networks 설명

1. Background

Facebook이나 Twitter의 network를 그래프로 표현한다고 해보자. 정말 거대한 그래프가 형성될 것이다. 대다수의 GNN 연구들은 작은 그래프 데이터셋에서 성능 측정이 이루어지는 경우가 많다. 복잡하고 많은 관계들을 고려해야 하다보니 자연스레 GNN의 최대 문제 중 하나는 바로 scalability라고 할 수 있다.

SIGN은 기존에 많이 시도되었던 node-level 및 graph-level sampling 방법을 취하지 않고도 scalability를 달성한 알고리즘이다. sampling 방법에 의존하지 않기 때문에 최적화에 있어 개입될 수 있는 bias를 줄일 수 있다는 장점을 지닌다. 여러 데이터셋에 대한 실험 결과를 제시하고 있는데, 사용된 데이터셋 중 하나는 ogbn-papers100M으로, 110m nodes와 1.5b edges를 갖고 있다.

2. Architecture

SIGN의 구조는 inception module에서 영감을 받아 만들어 졌다.

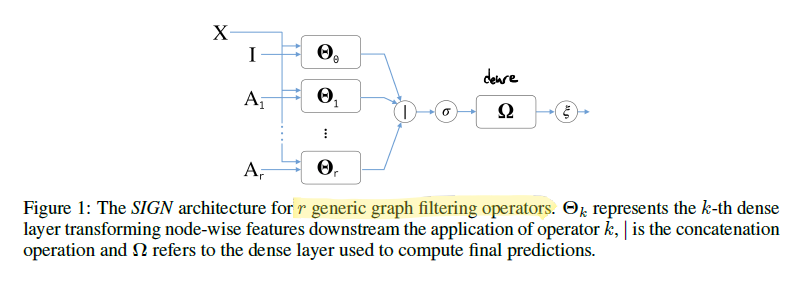
위 그림과 같이 SIGN은 여러 유형 및 크기의 graph convolutional filter를 조합하고 이 결과에서 GNN을 적용하여 downtream task에 활용하는 방식의 구조를 갖고 있다. 이 때 filter에서 수행되는 연산의 중요한 부분은 model parameter의 영향을 받지 않아 미리 계산이 가능하기 때문에 빠른 학습 및 추론이 가능하다.

논문에서도 언급하였듯이 SIGN은 go deep 이냐 go wide 이냐에 대한 물음에 대한 하나의 답을 제안한다고 볼 수 있다. 복잡한 graph 구조의 데이터에서 유의미한 정보를 추출하기 위해 deep network를 구성할 수도 있지만 SIGN과 같이 shallow network이지만 여러 접근(go wide) 방법을 통해 이를 달성할 수도 있는 것이다.

SIGN을 식으로 나타내면 아래와 같다.

$A$ 는 $(n, n)$, $X$ 는 $(n, d)$, $\theta$ 는 $(d, d^{\prime})$ 의 shape을 가진다. 따라서 이를 쭉 이어 붙이면 $Z$ 는 $(n, d^{\prime}(r+1))$ 의 shape을 갖게 될 것이다.

그렇다면 $\mathbf{A}_r \mathbf{X}_r$ 연산은 무엇일까. 일단 이 곱 연산에는 앞서 기술하였듯이 model parameter가 없기 때문에 미리 계산이 가능하다. graph가 크다면 이 역시 상당히 큰 연산이 되겠지만 병렬 시스템을 잘 이용하면 충분히 미리 계산할 수 있다고 설명하고 있다. 사실 이 부분이 SIGN의 가장 핵심 부분이다. $\mathbf{X}$ 는 node feature matrix가 될 것이다. 이렇게 하나의 matrix로 표현하였기 때문에 구조에 변형을 가하지 않으면 basic SIGN은 homogenous graph에만 적용이 가능하다. $\mathbf{A}_r$ 은 총 3가지 방법으로 계산될 수 있다.

1) power of simple normalized adjacency matrix
2) PPR based adjacency matrix
3) triangle-based adjacency matrix

논문에서는 위 3가지 operator를 조합하는 방식으로 실험 결과를 보여주고 있다. 1) 로 생각해보면, 주어진 인접 행렬에 대하여 여러 번 행렬 곱을 수행하여 새로운 인접 행렬을 얻는 작업으로 이해할 수 있다. PPR에 대해서는 이 글에서 간략한 설명을 확인할 수 있다.

3. Experiments & Insights

실험 결과에 대해서는 논문 원본을 참고하길 바란다. 여러 데이터셋에 대하여 성능과 수행 시간을 측정하였고, Hyperparameter tuning 과정에서도 상세하게 기술되어 있기 때문에 여러 인사이트를 얻을 수 있다.

대표적인 비교 대상은 ClusterGCN과 GraphSAINT 인데 두 알고리즘 모두 Scalability를 달성하기 위해 고안된 알고리즘들로 볼 수 있다.

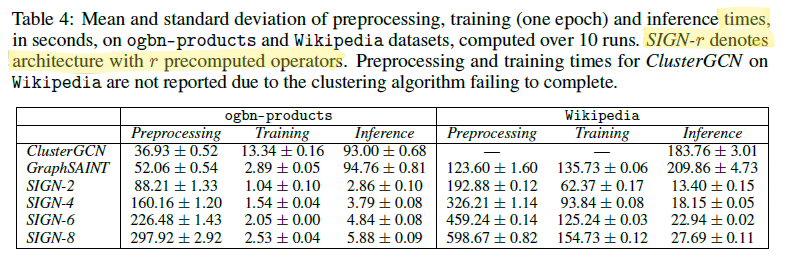
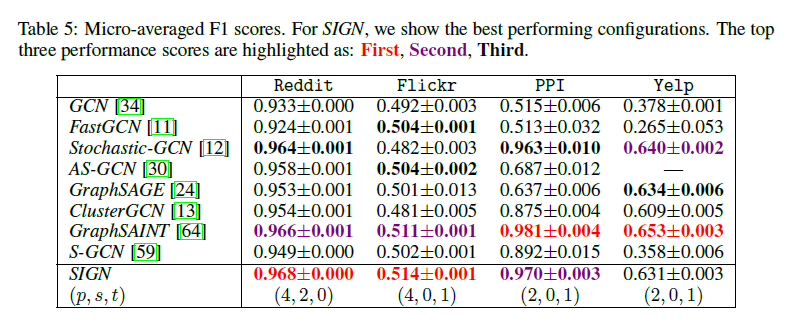
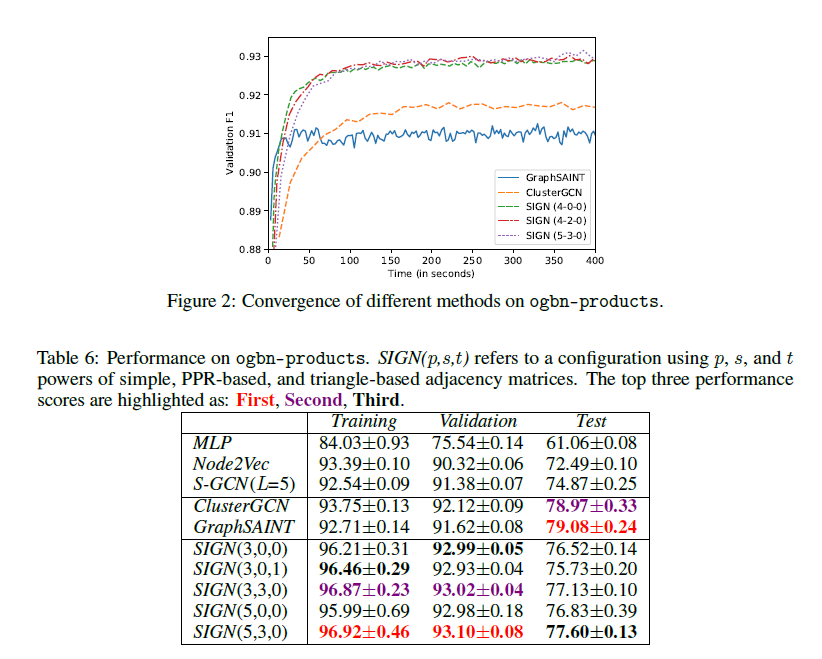
몇 가지 인사이트 및 알아두어야 할 부분을 정리하며 글을 마무리한다.

1) 기본적으로 SIGN은 굉장히 빠른 속도를 보여준다. 전처리에 있어 다소 추가적인 작업이 필요하긴 하지만 미리 계산이 가능하다는 이점 때문에 충분히 극복이 가능할 것으로 보인다.
2) 논문에서도 기술하였지만, $\Theta_i$, $\Omega$ 로 표기된 연산은 single-layer projection 연산으로 한정되는 것이 아니라 MLP로 대체될 수 있다. 이는 곧 이 부분에서 다른 형태의 GNN layer를 사용할 수 있음을 의미한다. 흥미로운 연구가 될 수 있을 듯 하다.
3) PPR-based adjacency matrix는 inductive setting에서는 형편 없는 결과를 보여주었다고 한다. 이러한 결과는 논문에서 언급된 한 참고문헌의 결과와도 일치하는 결과라고 한다.
4) $\mathbf{A}_r$ 연산을 학습 가능한 연산으로 로 대체할 수 있다. 이를 위해 graph attention 메커니즘을 생각해볼 수 있는데, node/edge feature의 특징을 활용하여 더욱 효과적인 결과물을 만들어 낼 수도 있을 것이다. 다만 그대로 적용할 경우 미리 계산할 수 있다는 SIGN의 장점을 잃어버리기 때문에 graph의 작은 subset으로 학습을 진행한 후 attention parameter를 고정하여 일괄적으로 적용하는 것을 추천하고 있다.

참고로 Pytorch Geometric에서는 torch_geometric.transforms.SIGN을 통해 SIGN 연산을 지원하고 있다. 다만 Source Code를 보면 확인할 수 있듯이 simple normalized adjacency matrix에 의한 연산만을 제공하고 있기에 다른 연산을 활용하고 싶다면 수정이 필요하다.