목차

• metapath2vec: Scalable Representation Learning for Heterogeneous Networks 설명
  • 1. Introduction
  • 2. Metapath2vec framework
  • 3. Experiments & Conclusion

이번 글에서는 Heterogenous Network에서 node representation을 학습하는 metapath2vec이란 논문에 대해 다뤄보겠습니다. 논문 원본은 이 곳에서 확인할 수 있습니다. 본 글에서는 핵심적인 부분에 대해서만 살펴보겠습니다.

그리고 관련하여 학습/분석 코드는 이 곳에 작성해두었으니 참고하셔도 좋을 것 같습니다.

metapath2vec: Scalable Representation Learning for Heterogeneous Networks 설명

1. Introduction

word2vec 기반의 network representation learning framework로는 DeepWalk, LINE, node2vec 등이 있고, 이들은 raw network로 부터 유용하고 의미있는 잠재적 feature를 자동적으로 발견해내는 역할을 수행합니다. 그러나 이들은 모두 homegenous network 기반의 알고리즘으로 여러 node/edge type이 존재하는 heterogenous network에서는 적용하기 어렵습니다.

본 논문은 heterogenous network에서 적용할 수 있는 meta-path-guided random walk strategy를 제시하고 있으며 이 방법론은 아래와 같은 특징을 갖습니다.

• 여러 다른 type의 node/relation에서 구조적이고 의미론적인 상관관계를 포착
• 복수의 node type 맥락 속에서 skip-gram 기반으로 network probability를 최대화
• 효과적이고 효율적인 heterogenous negative sampling 기법 적용
• similarity search, node classification, clustering 등에 적용 가능

논문에서는 metapath2vec과 이를 수정한 형태의 metapath2vec++를 제안하고 있습니다. 모든 node type에 대해서 같은 space에서 embedding을 생성하던 기존 방법과 달리 후자의 경우 각 node type 마다 별도의 space에서 embedding을 생성합니다.

2. Metapath2vec framework

hetegenous network는 $G=(V, E, T)$ 라고 하는 그래프로 정의됩니다. 이 때 여러 node/edge type을 표현하기 위한 mapping function이 존재합니다.

위에서부터 각각 node type, edge type을 결정합니다. 물론 $\vert T_v \vert + \vert T_E \vert > 2 $ 여야 할 것입니다. 만약 $=2$ 라면 homogenous network가 되겠지요.

metapath2vec의 embedding은 homegenous skip-gram model을 수정, 발전시킨 형태입니다. node $v$ 가 주어졌을 때, $N_t(v), t \in T_V$ 라는 heterogenous context를 갖는 확률을 최대화하는 node representation을 학습하는 것이 이 알고리즘의 목표입니다.

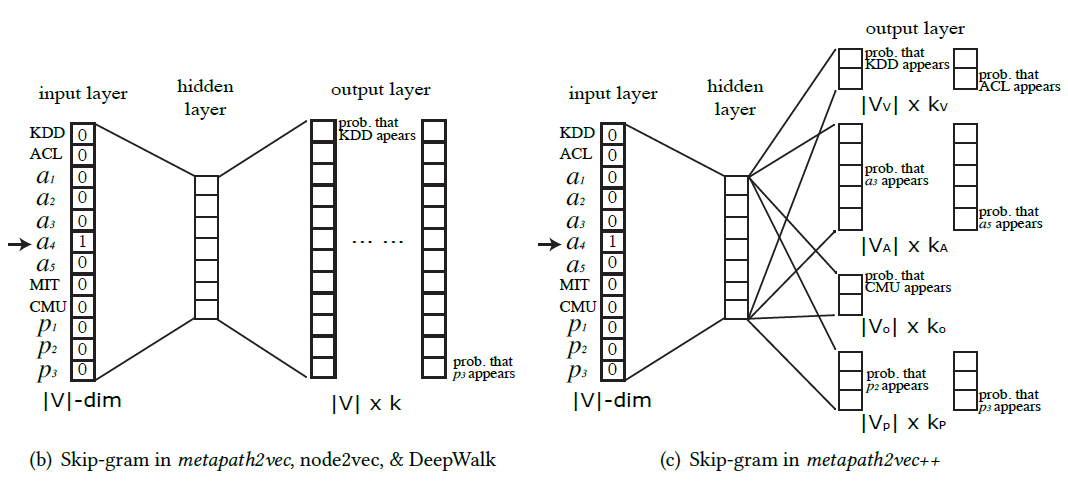
skip-gram 모델의 아이디어와 마찬가지로 중심 node가 있을 때 주변 node의 특성을 학습한다는 설정은 동일하지만, 이 때 적절한 node type에 따라 학습해야 하는 것입니다.

$p$ 함수는 softmax 함수이고, $N_t(v)$ 는 node type $t$ 을 갖는 $v$ 의 이웃을 의미합니다. $X_v$ 는 $\mathbf{X}$ 의 $v$ 번째 row로 node $v$ 의 embedding vector를 의미합니다. 좀 더 자세한 설명은 논문의 3페이지를 참고하길 바랍니다.

학습의 효율성을 증대하기 위해 negative sampling 기법이 적용되었습니다. metapath2vec은 다만 node type과 상관없이 negative sample을 추출하며, metapath2vec++은 이와 달리 node type specific하게 샘플링을 진행합니다.

meta-path scheme $\mathcal{P}$ 는 아래와 같이 정의할 수 있습니다.

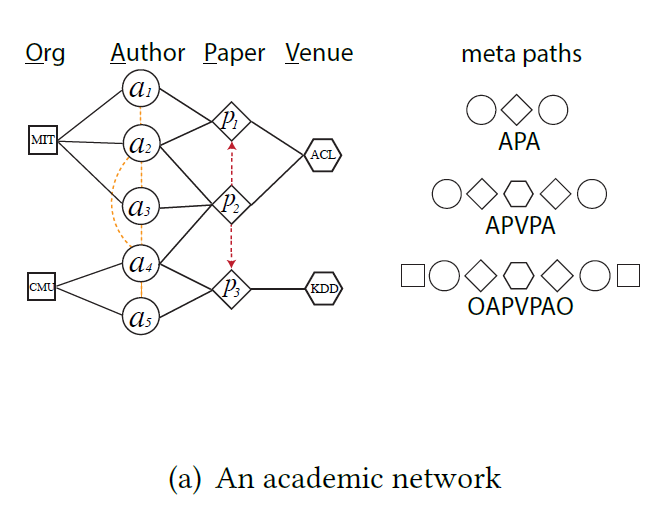
위 그림에서 예시를 들자면 APVPA는 2명의 작가가 어떤 paper를 냈고 이들이 같은 venue에서 accept되었다는 것을 의미합니다. 이러한 meta-path는 사실 metapath2vec에서는 domain 지식을 통해 사전에 설정되어야 합니다. 이는 많은 경우에 단점이 될 수 있는데, 이렇게 사전에 meta-path를 설정하기 어려운 경우가 많고, 어떤 path가 유의미한지 인간이 판단하기 어려울 때가 많기 때문입니다. 참고로 meta-path를 굳이 사전에 설정하지 않아도 자동적으로 찾는 기법을 고안한 논문으로는 Graph Transformer Networks가 있습니다.

metapath2vec에서 step $i$ 에서의 transition probability는 아래와 같이 정의합니다.

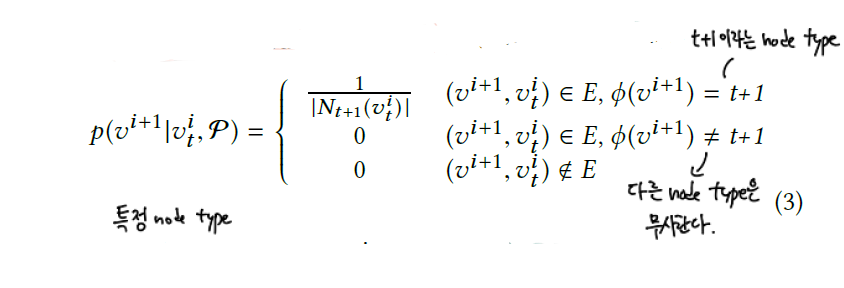
앞서 설명하였다시피 metapath2vec은 softmax 함수에서 node type 정보를 무시합니다. 이를 수정한 버전이 metapath2vec++입니다. 이 방법에서 softmax 함수는 context $c_t$ 의 node type에 따라 normalized됩니다. 이렇게 함으로써 skip-graph 모델의 output layer에서 각 type에 맞는 multinomial distribution을 정의할 수 있게 되는 것입니다.

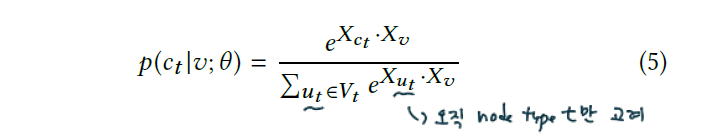
목적함수는 아래와 같습니다.

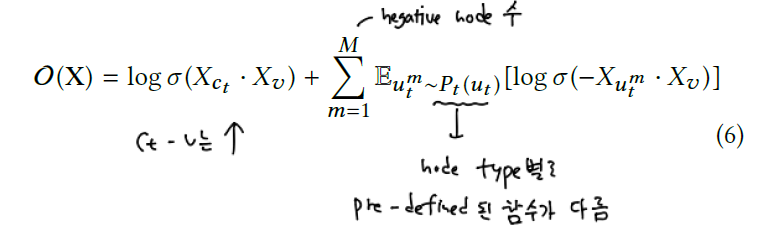
알고리즘의 pseudo code는 아래와 같습니다.

3. Experiments & Conclusion

실험을 위해 2가지 데이터셋이 사용되었습니다. 자세한 사항은 논문을 참조하시길 바랍니다. 두 데이터 모두 author, paper, venue의 관계를 탐색합니다.

실험에서 주목할만한 결과만 간단히 기록하겠습니다.

• Multiclass 분류 문제에서는 Macro F-1, Micro F-1 score를 통해 평가가 진행되었습니다. (이 metric은 이 곳에서 설명을 확인할 수 있습니다.) 대체적으로 metapath2vec 계열의 성능이 우수하였는데 특히 적은 데이터를 사용한 구간(전체 데이터의 20% 이하를 사용)에서의 성능이 돋보였습니다.

• node별 walk 수, walk length, embedding dim, neighborhood size라는 4개의 parameter에 대해서 sensitivity test를 해보았는데, 값을 더 늘린다고 성능이 향상되지는 않았습니다. 이는 곧 적당히 효율적인 size로 충분한 효과를 발휘할 수 있음을 증명합니다.

• Normalized Mutual Information을 metric으로 하여 node clustering 성능도 측정하였는데, metapath2vec 계열의 성능이 더욱 우수하였습니다.

• 다른 알고리즘과 달리 metapath2vec++은 정확히 node type을 구분하면서도 실제 관련이 높은 node 사이의 거리를 가깝게 만드는데 성공한 것으로 보입니다.

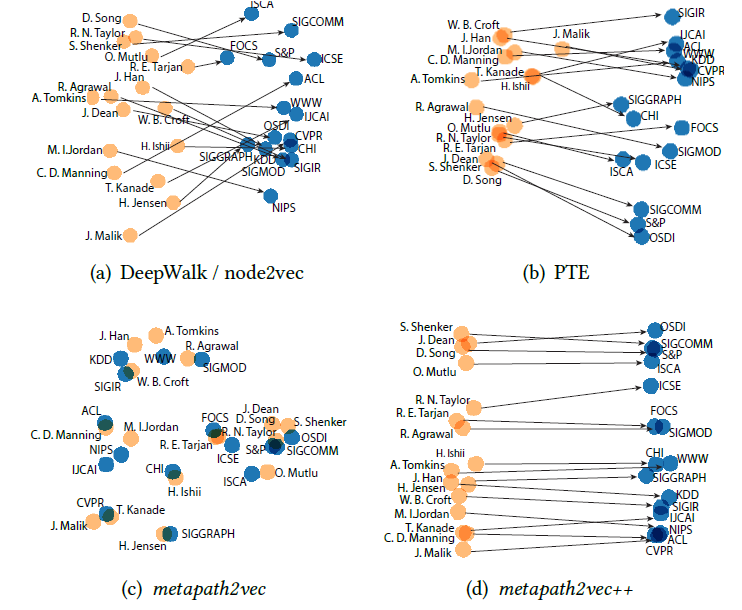
글 서두에서도 밝혔듯이 metapath2vec과 metapath2vec++은 heterogenous graph에서 구조적인 node representation learning을 가능하게 한 효과적인 방법론입니다. 핵심적인 아이디어가 돋보인 논문이고 그렇기 때문에 추후에 진행된 많은 연구에서 언급되고 있는 것으로 보입니다.

몇 가지 한계점도 있습니다. 일단 large intermediate output data가 존재할 때 학습하는 것이 쉽지 않습니다. 그리고 meta-path를 사전에 설정하는 해야 하는 것도 때때로 문제가 됩니다.