이 글에서는 2018년 6월 Alec Radford 등이 발표한 OpenAI GPT-1: Improving Language Understanding by Generative Pre-Training를 살펴보도록 한다.

코드와 논문은 여기에서 볼 수 있다.

중요한 부분만 적을 예정이므로 전체가 궁금하면 원 논문을 찾아 읽어보면 된다.

OpenAI GPT-1 - Improving Language Understanding by Generative Pre-Training

논문 링크: OpenAI GPT-1 - Improving Language Understanding by Generative Pre-Training

홈페이지: OpenAI

Tensorflow code: Official Code

초록(Abstract)

자연어이해는 원문함의, 질답, 의미 유사성 평가, 문서분류 등 넓은 범위의 과제로 이루어져 있다. 미분류 상태의 큰 말뭉치가 풍부함에도, 이러한 특정 과제의 학습을 위한 분류된 데이터는 부족하며, 모델이 적절히 수행하도록 만드는 것을 어렵게 한다.
이 논문에서는 이러한 과제들에서의 큰 성능 향상은, 언어모델을 다양한 미분류 말뭉치로 생성적 사전학습(generative pre-training)을 시킨 후 각 특정 과제에 맞춘 미세조정(fine-tuning) 과정을 거쳐 가능하다. 이전의 접근법과는 달리 모델구조는 최소한으로 변화시키면서 효과적인 전이(transfer)를 얻기 위한 미세조정 단계에서 과제에 맞는 입력표현(input representations)을 사용했다. 그리고 이 접근법이 다양한 과제에 대해 효과적임을 보일 것이다.

이 논문에서 제시하는 과제에 대한 별다른 지식이 없는(task-agnostic) 모델은 특정과제에 특화된 구조를 사용하는 모델의 성능을 뛰어넘는데 연구된 12개의 과제 중 9개에서는 state-of-the-art를 달성하였다. 예를 들어 상식추론(Cloze)에서는 8.9%, QA에서는 5.7%, 원문함의에서는 1.5% 상승하였다.

1. 서론(Introduction)

원본 그대로의 텍스트에서 효과적으로 학습하는 능력은 NLP에서 지도학습에 대한 의존성을 낮추는 데 있어 매우 중요하다. 대부분의 딥러닝 방법은 수동으로 분류된 방대한 양의 데이터를 필요로 하는데 이는 분류된 자원의 부족으로 인한 많은 범위로의 응용에 제약을 건다. 이러한 상황에서 미분류 데이터로부터 언어적 정보를 얻어낼 수 있는 모델은 힘들게 분류된 데이터를 만드는 것의 훌륭한 대안이 될 뿐만 아니라, 괜찮은 지도 방법이 있다 하더라도 비지도학습이 더 좋을 결과를 얻기도 한다. 사전학습된 단어 embedding이 그러한 예이다.

그러나 미분류 텍스트에서 단어 수준 정보 이상의 것을 얻는 것은 다음 두 가지 이유로 어렵다.

1. 어떤 최적화 목적함수가 전이(transfer)에 유용한 텍스트 표현(representation)을 배우는 데 효과적인지 불분명하다. 최근 연구들은 언어모델링이나 기계번역, 담화 일관성(discourse coherence) 등 다양한 objective에서 각 방법이 다른 과제에서는 다른 방법을 능가하는 것을 보여 왔다.
2. 학습된 표현을 다른 과제로 전이하는 가장 효과적인 방법에 대한 일치된 의견이 없다. 존재하는 방법들은 복잡한 학습전략이나 부가 학습 목적함수를 더하는 등 모델 구성에 과제에 특화된(task-specific) 변화를 주어야 한다.

이러한 불확실성은 언어처리에 대한 효과적인 준지도학습 접근법의 개발을 어렵게 한다.

이 논문에서는 비지도 사전학습(unsupervised pre-training)과 지도 미세조정(supervised fine-tuning)의 조합을 사용하여 언어이해 과제를 위한 준지도학습 접근법을 탐색한다. 목표는 약간의 조정만으로 넓은 범위의 과제에 전이 및 적용할 수 있는 범용 표현을 학습하는 것이다. 미분류 대량의 말뭉치와 수동으로 주석을 단(annotated) 학습예제를 갖는 여러 dataset에 대한 접근가능을 가정한다. 또한 학습은 두 단계를 거치게 된다.

1. 신경망모델의 초기 parameter를 학습하기 위해 미분류 데이터에 대한 언어모델링 목적함수를 사용한다.
2. 이 parameter를 연관된 지도 목적함수를 사용하여 목표 과제에 적용시킨다.

모델 구성은 기계번역, 문서생성, 구문분석 등에 상당한 성능을 보이는 Transformer를 사용한다. 이 모델은 RNN 등에 비해 장거리 의존성을 다루는 데 뛰어나 더 많은 구조화된 memory를 쓸 수 있게 한다. 전이 중에는 traversal-style 접근법에서 얻은 과제특화된 입력적응을 이용하며 입력은 한 개의, 일련의 ‘연속된 token’으로 주어진다. 이러한 적응방법은 사전학습된 모델의 구조를 바꾸는 것을 최소화한다.

이 접근법을 네 가지(자연어추론, 질답, 의미 유사성, 문서분류)에 대해 평가한다. 과제에 대한 지식이 없는 이 범용 모델은 12개 중 9개의 과제에서 state-of-the-art 결과를 보이며 선전했다.

2. 관련 연구(Related work)

Semi-supervised learning for NLP

이 연구는 자연어의 준지도학습에 넓게 걸쳐 있다. 이 체계는 sequence labeling이나 문서분류 등의 응용에 큰 관심을 불러일으켰다.

초기의 연구는 나중에 지도모델의 특징으로 사용될, 단어수준이나 구 수준의 통계를 계산하기 위해 미분류 데이터를 사용했다. 지난 몇 년간 연구자들은 미분류 말뭉치로부터 학습된 단어 embedding의 장점(다양한 과제에서의 성능 향상 가능성)을 발견했다. 그러나 이 접근법은 주로 단어 수준 표현을 학습할 뿐이다.

최근의 연구는 미분류 데이터로부터 단어수준 이상의 정보를 학습하려 하고 있다. 구 수준이나 문장 수준의 embedding은 미분류 데이터로부터 학습될 수 있으며 다양한 문제에서 텍스트를 적절한 벡터표현으로 변환할 수 있다.

Unsupervised pre-training

목표가 지도학습 목적함수를 수정하는 것이 아닌 좋은 초기화 지점을 찾는 것일 때, 비지도 사전학습은 준지도학습의 특별한 경우가 된다. 초기에는 이미지 분류나 회귀문제에 사용했다. 후속 연구는 사전학습이 정규화처럼 동작하며 DNN에서 더 좋은 일반화를 가능하게 함을 보였다. 최근에는 이미지분류, 음성인식, 다의어 명확화, 기계번역 등에 사용되고 있다.

GPT와 가장 유사한 연구는 신경망을 언어모델링 목적함수를 사용하여 사전학습시키고 지도 하에 목표 과제에 맞춰 미세조정하는 것을 포함한다. 그러나 어떤 언어적 정보를 포착하는 데 있어 LSTM의 사용은 이를 좁은 범위에 한정시킨다. 하지만 Transformer를 사용함으로써 넓은 범위에 걸친 언어적 구조와 정보를 학습할 수 있게 하였고 나아가 다양한 과제에 사용할 수 있게 되었다.
다른 접근법은 목표 과제에 맞춘 감독학습 중에 사전학습된 언어/기계번역 모델에서 얻은 은닉표현을 부가정보르 사용하였는데 이는 상당한 양의 parameter를 추가하는데, GPT는 그렇지 않다.

Auxiliary training objectives

보조 학습 목적함수를 추가하는 것은 준지도학습의 대안이다. A unified architecture for natural language processing deep neural networks with multitask learning이 여러 NLP task에 사용되었으며, 최근에는 Semi-supervised Multitask Learning for Sequence Labeling이 목표 과제에 보조 언어모델링 목적함수를 추가해 sequence labeling task에서 성능향상을 얻었다. GPT도 보조목적함수를 추가하지만, 비지도 사전학습이 이미 목표 과제에 대한 여러 언어적 정보를 학습했다는 것을 보일 것이다.

3. Framework

학습은 두 단계로 진행된다.

1. 큰 말뭉치에서 대용량의 언어모델을 학습한다.
2. 분류 데이터를 써서 특정 과제에 맞춰 모델을 미세조정한다.

3.1. Unsupervised pre-training

token의 비지도 말뭉치 $\mathcal{U} = {u_1, …, u_n}$이 주어질 때, 다음 우도를 최대화하도록 표준언어모델링 목적함수를 사용한다:

[L_1(\mathcal{U}) = \sum_i \log P(u_i \vert u_{i-k}, …, u_{i-1}; \Theta)]

$k$는 문맥고려범위(context window)이고 조건부확률 $P$는 parameter가 $\Theta$인 신경망을 사용하도록 설계된다. 이들은 확률적 경사하강법(SGD)에 의해 학습된다.

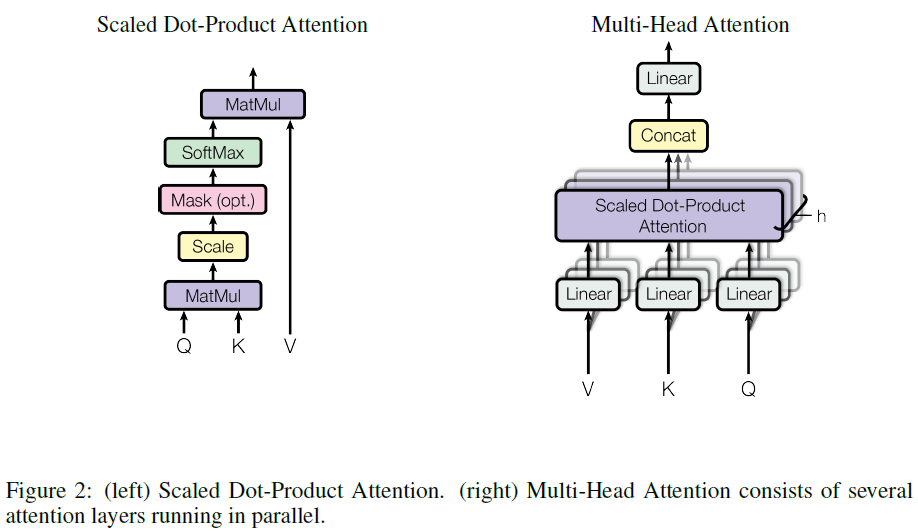
GPT는 언어모델로 Transformer의 변형인 multi-layer Transformer decoder를 사용한다. 이 모델은 입력 문맥 token에 multi-headed self-attention을 적용한 후, 목표 token에 대한 출력분포를 얻기 위해 position-wise feedforward layer를 적용한다:

[h_0 = UW_e + W_p \qquad \qquad \qquad \qquad \ \ \qquad]

[h_l = \text{transformer_block}(h_{l-1}) \ \ \forall l \in [1, n]]

[P(u) = \text{softmax}(h_n W_e^T) \qquad \qquad \qquad \quad \ \ \qquad]

$U = (u_{-k}, …, u_{-1})$는 token의 문맥벡터, $n$은 layer의 수, $W_e$는 token embedding 행렬, $W_p$는 위치 embedding 행렬이다.

(참고: 논문에는 위 식에서 $\forall l$이 $\forall i$로 오타가 나 있다)

3.2. Supervised fine-tuning

위 $L_1(\mathcal{U})$ 우도에 따라 모델을 학습시키고 나면, parameter를 목표 과제에 맞춰 미세조정한다. 분류된 dataset $\mathcal{C}$이 있고 각 구성요소가 일련의 입력 token $x^1, …, x^m$ 및 그 정답(label) $y$로 되어 있다고 하자. 입력은 최종 transformer block의 활성값 $h_l^m$을 얻기 위해 위의 사전학습된 모델에 전달하고 이 결과는 다시 $y$를 예측하기 위해 parameter $W_y$와 함께 선형 출력층으로 전달된다:

[P(y \vert x^1, …, x^m) = \text{softmax}(h_l^m W_y)]

이는 다음 우도를 최대화하도록 한다:

[L_2(\mathcal{C}) = \sum_{(x, y)} \log P(y \vert x^1, …, x^m)]

미세조정 단계에 언어모델을 보조 목적함수로 포함시키는 것은 다음 이유에서 학습을 돕는다.

• 지도 모델의 일반화를 향상시키고
• 수렴을 가속화한다.

이는 이전 연구들과 결을 같이한다.

구체적으로, weight $\lambda$에 대해 다음 목적함수를 최적화한다:

[L_3(\mathcal{C}) = L_2(\mathcal{C}) + \lambda \ast L_1(\mathcal{C})]

종합적으로, 미세조정 단계에서 추가된 parameter는 $W_y$과 구분자 token을 위한 embedding 뿐이다.

3.3. Task-specific input transformations

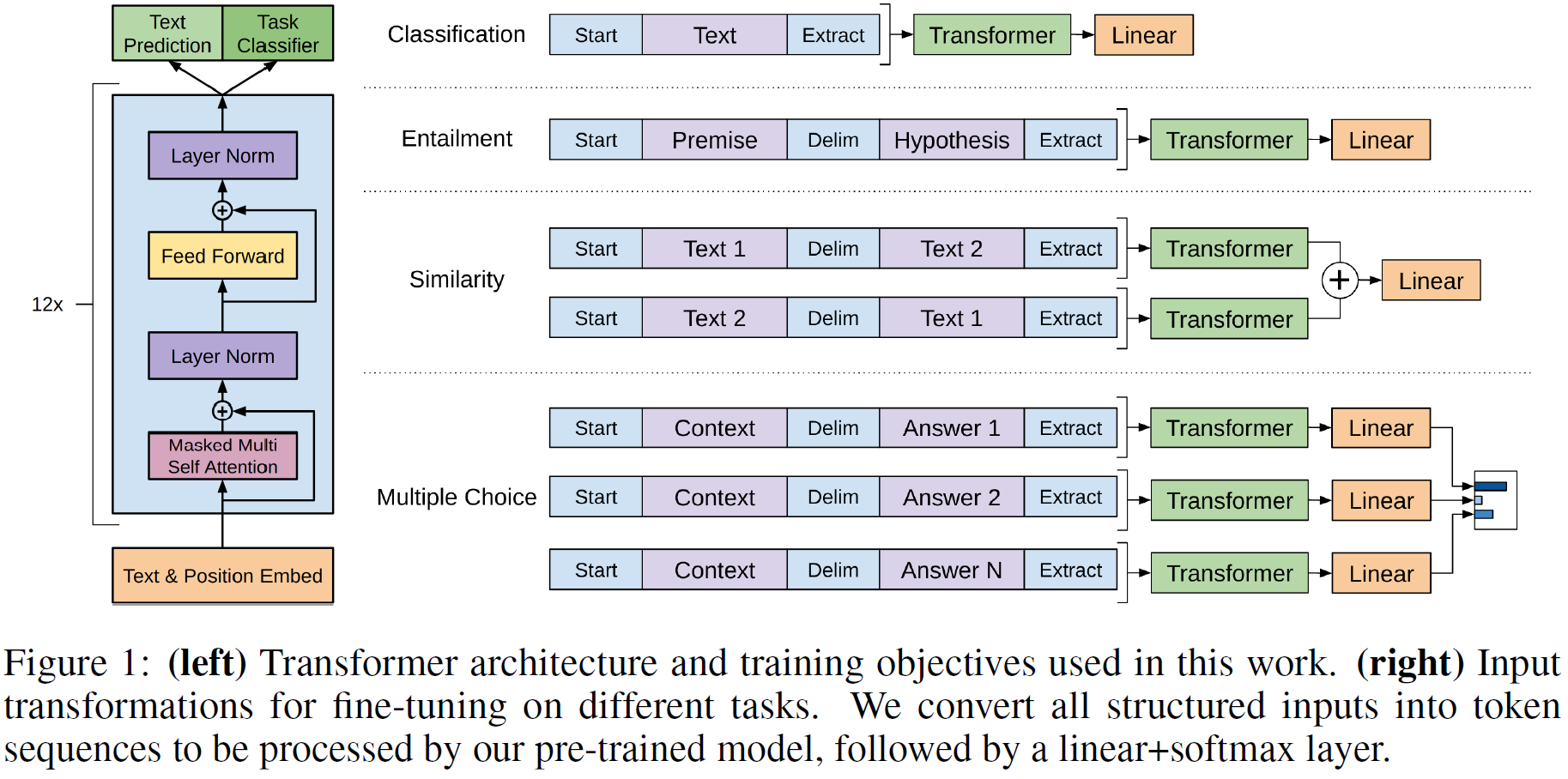
텍스트 분류와 같은 몇몀 과제에 대해서는 모델 미세조정을 위에서 언급한 방법으로 직접 할 수 있다. 그러나 질답과 원문함의와 같은 과제에서는 입력 형태가 문장의 2~3개 쌍인 등 많이 다르므로 이를 처리해주어야 한다. 그 방법은 아래 Figure 1에 나와 있는데, 질문/텍스트/선택지/가정/전제 등을 하나씩 따로 구분자(delimiter)로 구분하여 하나로 연결하는 방식을 쓴다. 구체적인 방법은 다음과 갈다.

Textual entailment

함의 문제에서는 전제 $p$와 가정 $h$를 구분자 $로 연결하였다.

Similarity

두 개의 텍스트 사이에 순서가 딱히 없으므로 텍스트 두 개를 다른 순서로 이어붙여 총 2개를 입력으로 쓴다. 이는 각각의 Transformer에 입력으로 들어간다.

Question Answering and Commonsense Reasoning

문맥 문서 $z$, 질문 $q$, 가능한 답변 ${a_k}$이라 하면, [z; q; $; a_k]로 연결하고 입력의 개수는 답변의 개수만큼 생성된다.

4. 실험(Experiments)

4.1. Setup

Unsupervised pre-training

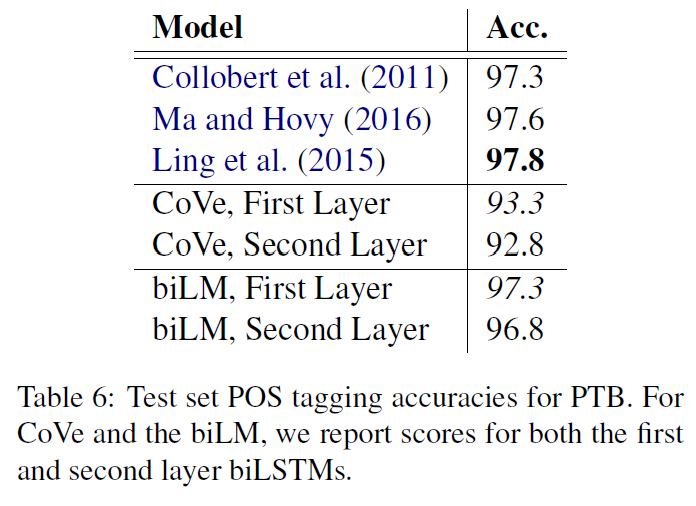
언어모델을 학습하기 위한 dataset으로 7천 개의 다양한 분야의 미출판 책에 대한 내용을 포함하는 BooksCorpus를 사용한다. 이는 특히 넓은 범위에 걸친 언어적 정보를 포함하기에 중요하다. 대안이 되는 dataset으로는 ELMo에서 사용된 1B Word Benchmark가 있다. 이는 크기는 비슷하지만 문장들이 서로 섞여 있어 장거리 의존정보가 파괴되어 있다.

사용하는 dataset 정보는 아래와 같다.

Model specifications

Transformer의 세부 세팅을 대부분 따르지만, Encoder-Decoder 중 Decoder만 사용한다. 이 decoder는 원본은 6번 반복되지만, GPT는 12번 반복한다.

논문에는 안 나와있지만 모델의 크기는 parameter가 117M개이다.

Fine-tuning details

비지도 사전학습에서 사용한 hyperparameter를 그대로 사용했다. $p=0.1$의 dropout을 추가했다.
learning rate는 6.25e-5와 batch size는 32, 미세조정은 3 epoch 동안 진행되었으며 learning rate decay는 warmup을 포함해 각 학습당 0.2%였고, $\lambda=0.5$이다.

4.2. Supervised fine-tuning

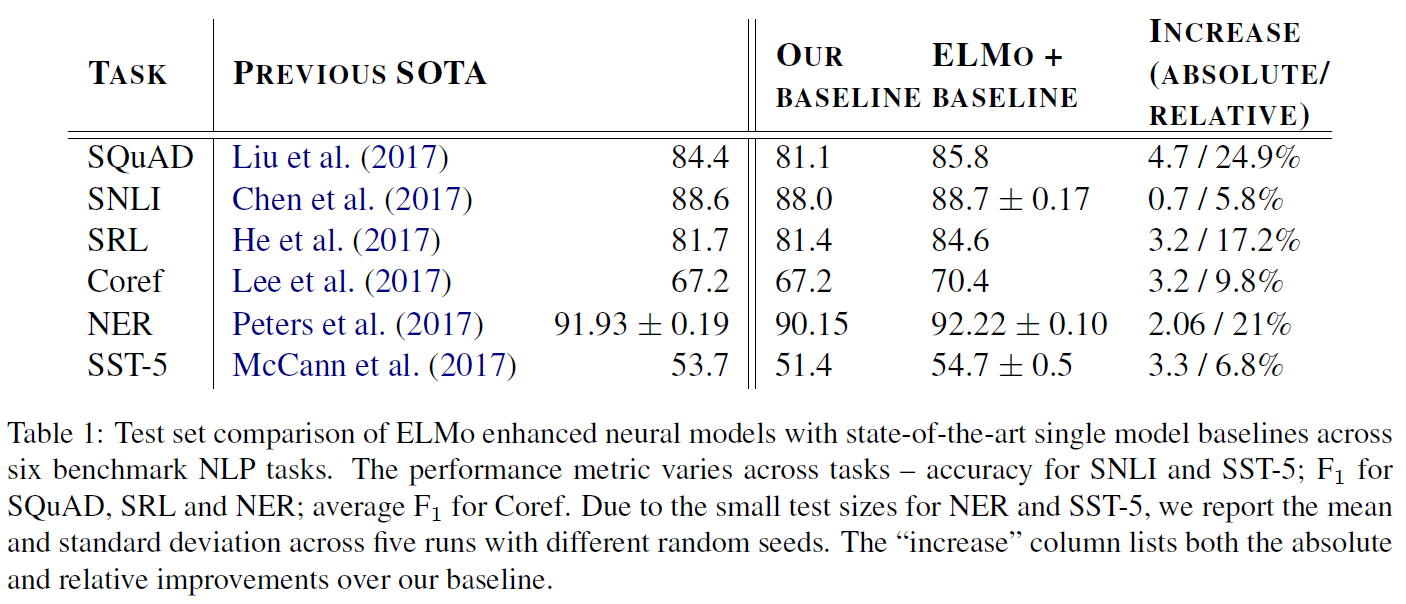
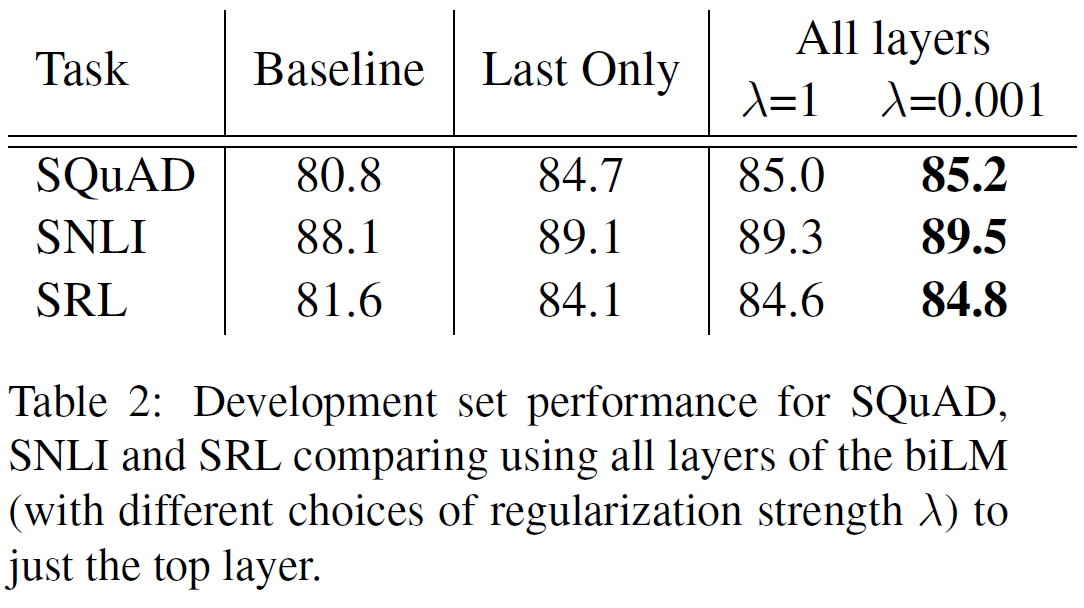
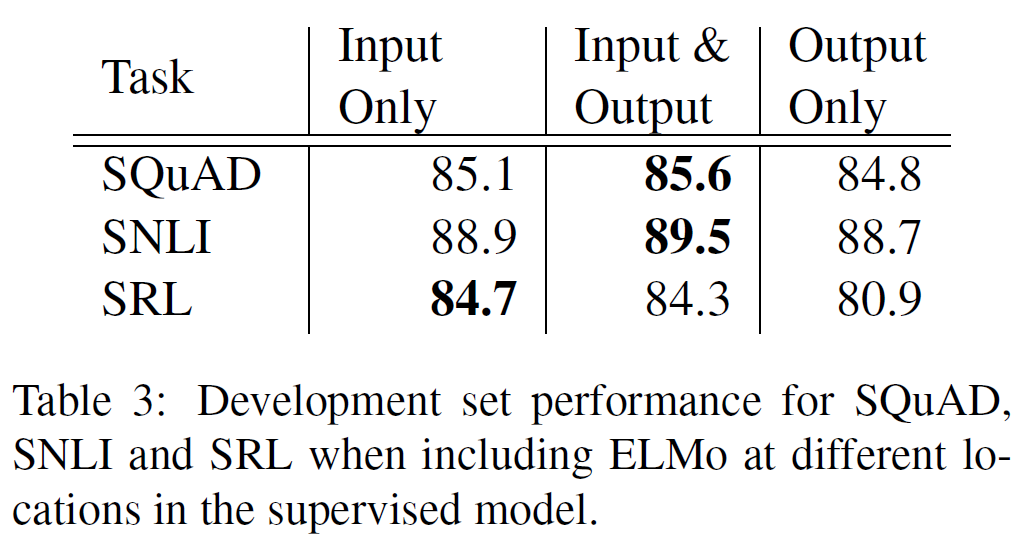
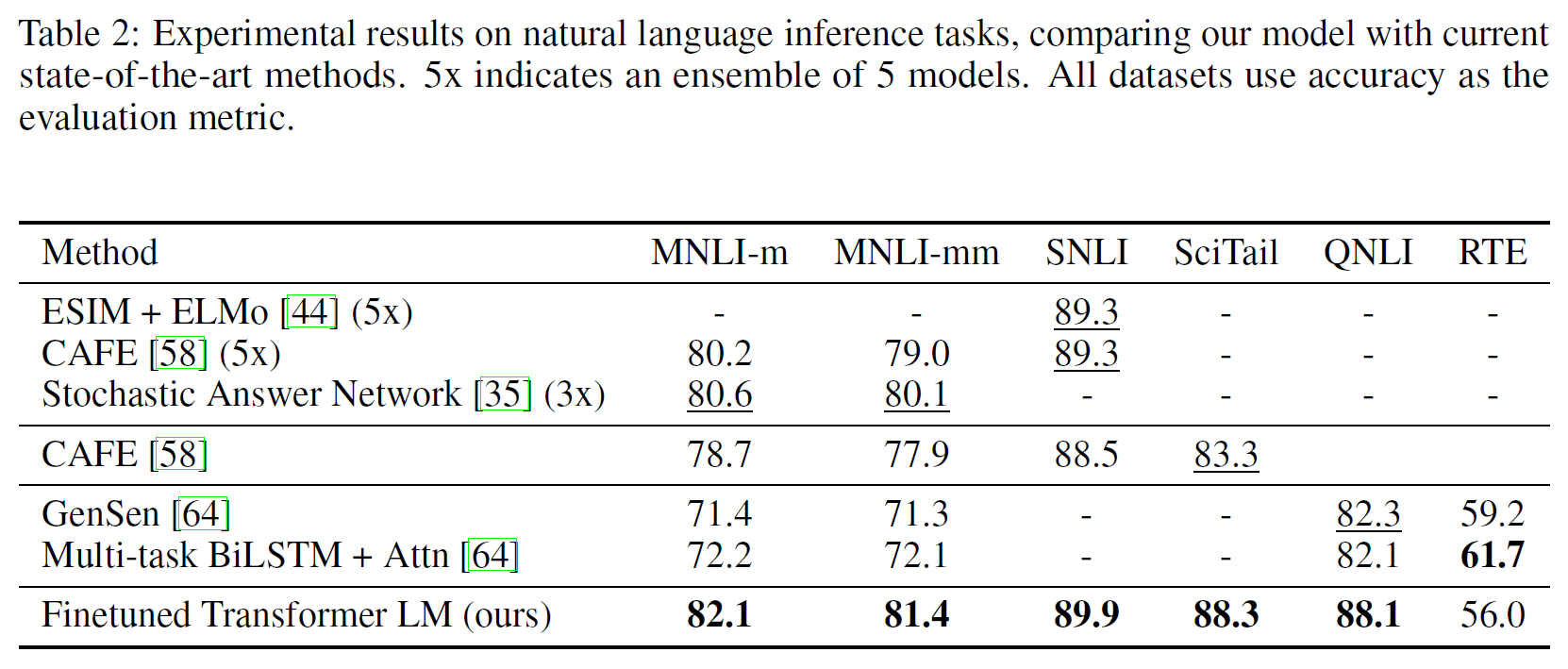
자연어추론, 질답, 의미유사성, 문서분류에 대해 평가를 진행하였으며 이 중 일부는 GLUE benchmark에 포함되어 있다. 결과는 아래 Table 2, 3에 있다.

Natural Language Inference

Image caption(SNLI), 문서화된 음성, 대중소설, 정부 보고서(MNLI), 위키피디아 기사(QNLI), 과학시험(SciTail), 뉴스기사(RTE) 등의 다양한 데이터로 실험하였다. 각 0.6~5.8% 정도 성능이 향상되었다.

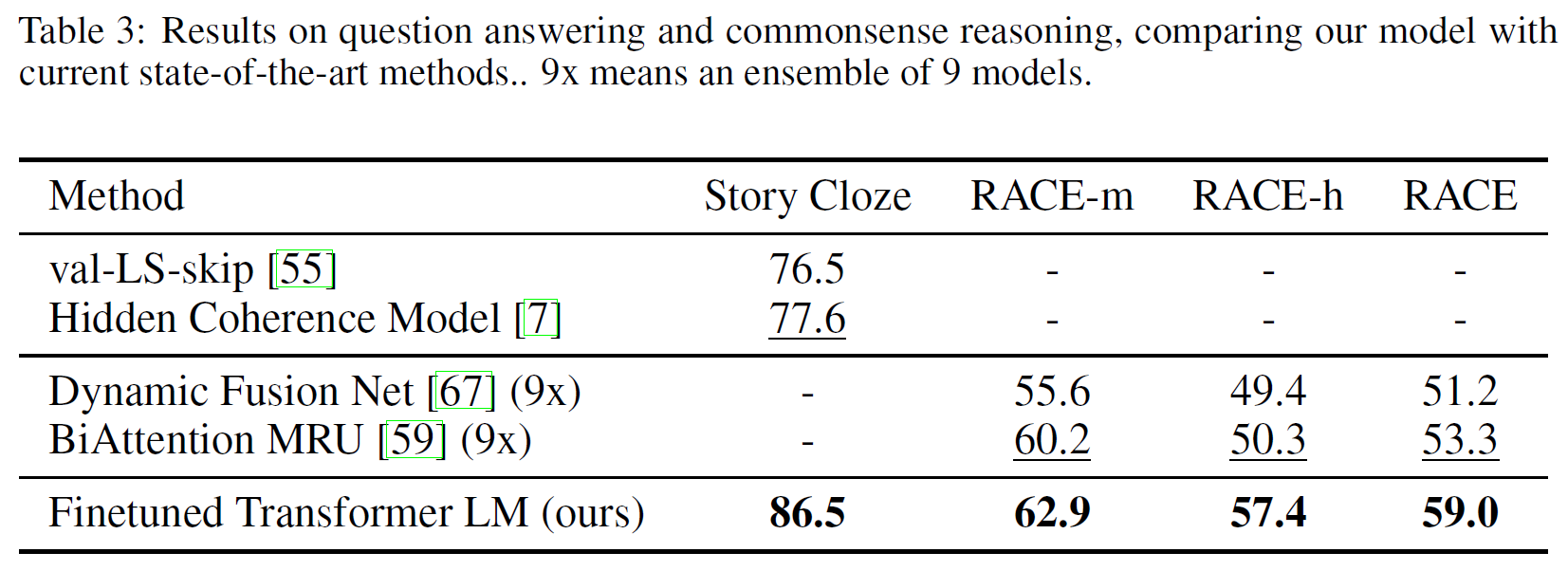
Question answering and commonsense reasoning

중고등학교 시험에서 나온 영어지문과 관련 질문으로 구성된 RACE dataset으로 진행하였다. 또 Story Cloze에 대해서도 진행했는데 이는 무려 8.9%까지 높은 성능을 내며 결과를 종합했을 때 GPT가 넓은 범위에 걸친 문맥 정보도 잘 포착해냄을 알 수 있다.

Semantic Similarity

QQP에 대해서는 BiLSTM + ELMo + Attention을 사용한 모델보다도 특히 성능이 향상되었다.

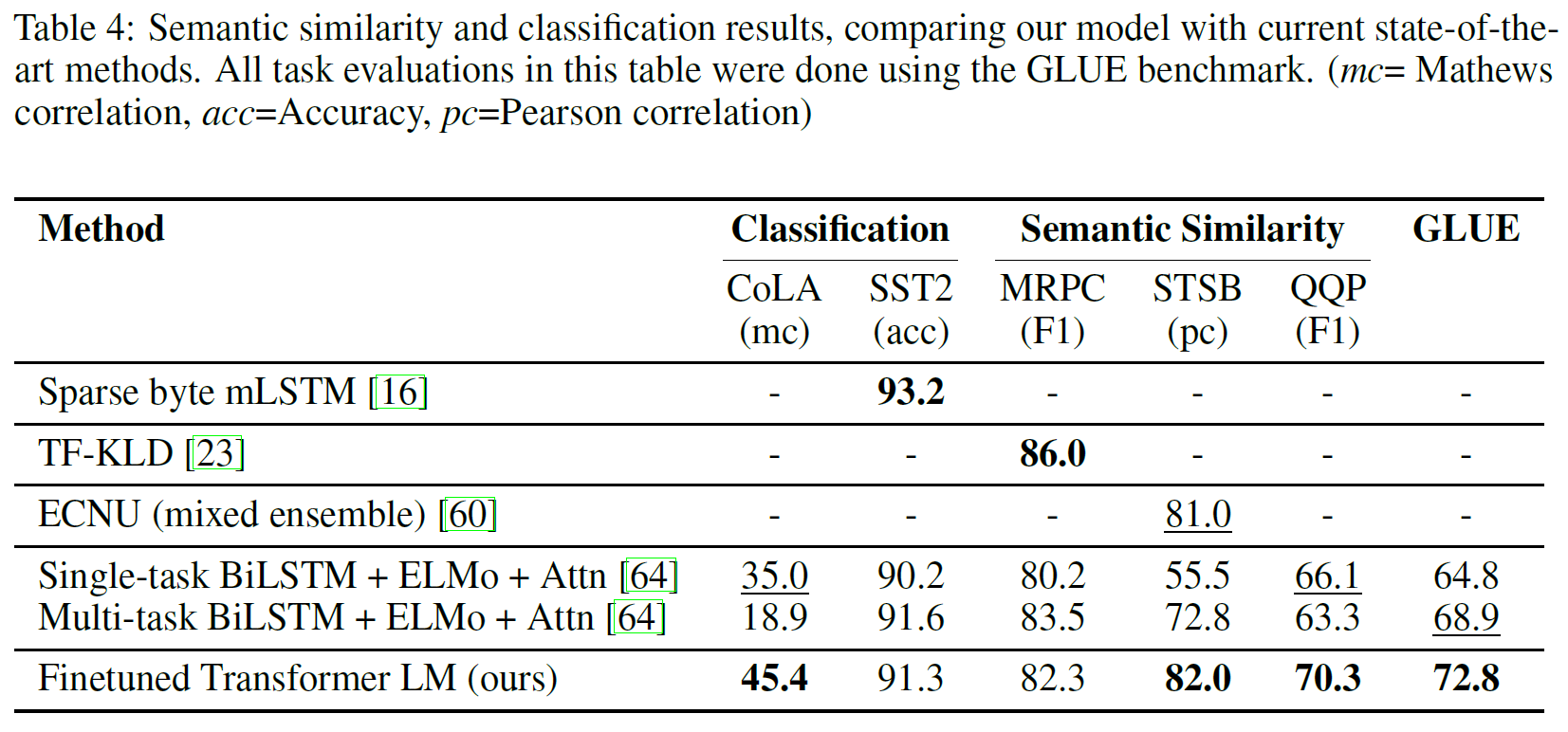
Classification

두 개의 다른 텍스트 분류 과제에 대해서도 평가를 진행했다. CoLA(The Corpus of Linguistic Acceptability)는 어떤 문장이 문법적으로 옳은지를 전문가가 평가한 답변과, 학습된 모델에 대한 언어적 편향에 대한 테스트를 포함한다. SST-2(The Stanford Sentiment Treebank)는 표준 이진 분류 문제이다. CoLA에 대해서는 35.0 $\to$ 45.4점으로, SST-2에서는 68.9 $\to$ 72.8점으로 상승하였다.

종합하면, 12개의 task 중 9개에서 state-of-the-art를 달성하였다.

5. 분석(Analysis)

Impact of number of layers transferred

아래 Figure 2의 왼쪽은 layer의 수를 다르게 하면서 RACE와 MultiNLI에 대해 실험을 진행한 것인데, transferring embedding이 성능 향상을 가져오며, 각 transformer layer 당 9%까지 향상시킨다(on MultiNLI)는 내용이다. 이는 사전학습된 모델의 각각의 layer가 문제를 푸는 데 있어 유용한 기능을 포함한다는 것을 의미한다.

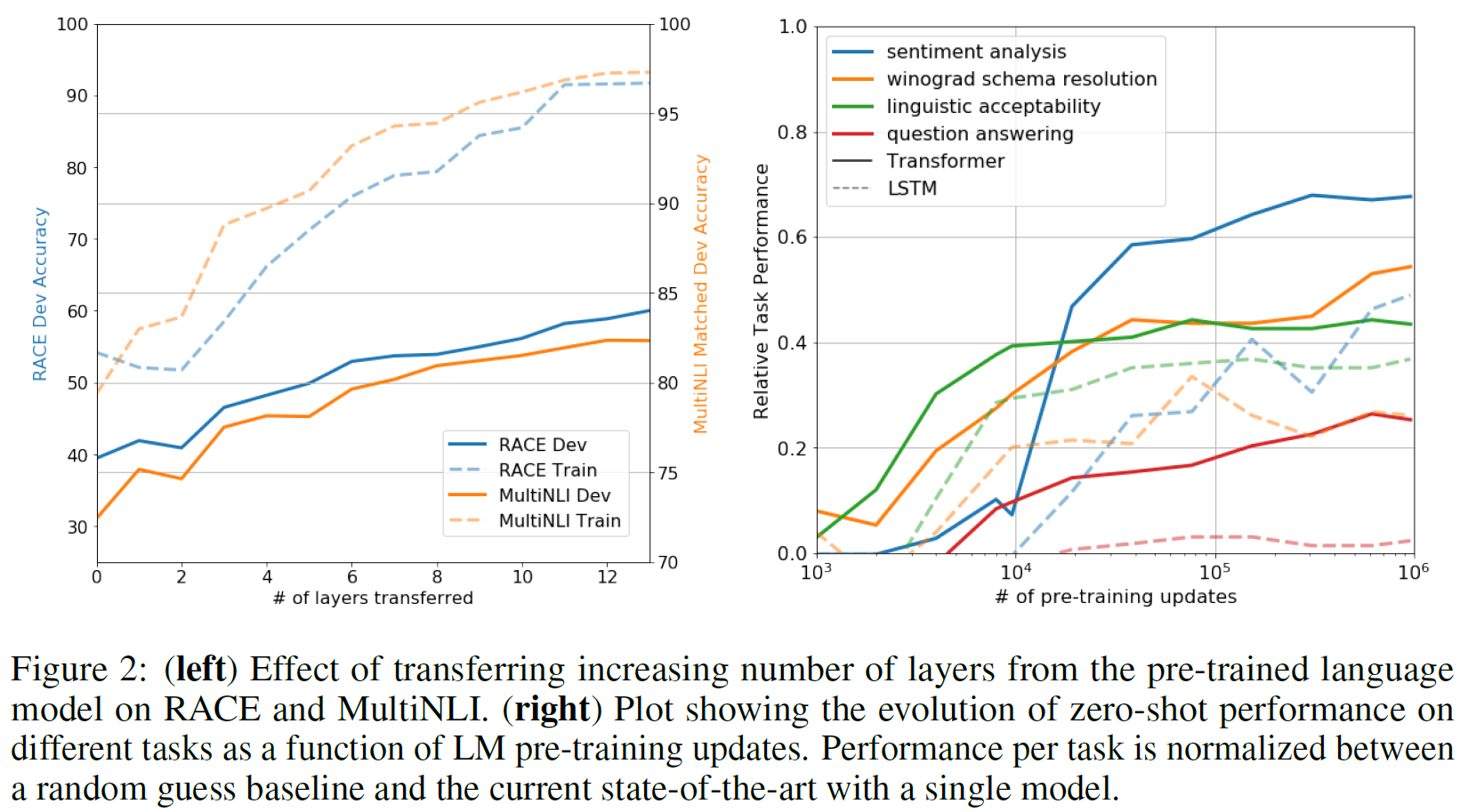
Zero-shot Behaviors

저자는 근본적인 generative model이 LM capability를 향상시키기 위해 많은 task를 수행하는 법을 배울 수 있고, LSTM과 비교해서 transformer의 attentional memory가 transfer에 도움이 된다고 가정하였다 Transformer를 통한 언어모델의 사전학습이 효과적인지에 대한 가정이 하나 있다. 기반 생성모델은 언어모델링 역량을 향상시키기 위해 평가에 포함된 여러 과제를 수행하는 것을 학습하였으며, Transformer의 attentional memory는 LSTM에 비해 전이를 더 원활하게 해 준다는 것이다. 지도 미세조정 없이 과제를 수행하기 위해 기반 생성모델을 사용하는 일련의 체험적 해결책(heuristic solutions)을 사용했다. 이 결과를 위 Figure 2의 오른쪽 부분에 시각화하였다.
이 체험적 해결책의 성능은 안정적이며 학습에 따라 꾸준히 증가하는 것으로 보아 생성적 사전학습은 과제와 관련된 넓은 범위의 기능성(functionality)의 학습을 뒷받침한다. 또한 LSTM은 zero-shot 성능에서 큰 편차를 보여 Transformer 구조의 귀납적 편향이 전이를 돕는다고 할 수 있다.

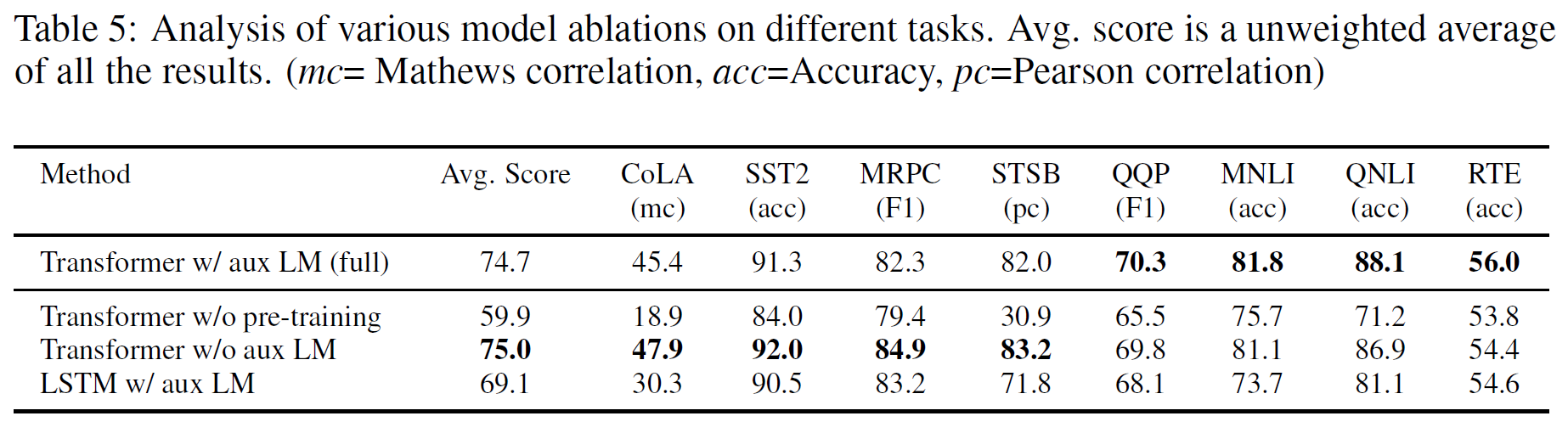
Ablation studies

세 가지 분석을 수행하였다.

1. 미세조정 단계에서 보조 LM 목적함수는 NLI task와 QQP에 도움을 주는데, 큰 dataset에서는 이점이 있지만 작은 dataset에서는 그렇지 못함을 보여준다.
2. Transformer을 같은 구조의 2048 unit의 LSTM로 대체하였는데 5.6점의 점수 하락이 있었다. 성능이 좋은 경우는 MRPC 뿐이었다.
3. Transformer를 사전학습 없이 바로 지도학습을 하도록 해보았는데, 14.8%의 성능 하락이 있었다.

6. 결론(Conclusion)

생성적 사전학습과 특정과제에 특화된 미세조정을 통해 학습된, 과제에 대해 별다른 지식이 없으며 자연어이해 능력이 뛰어난 단일 모델(framework)를 소개하였다. 넓은 범위에 걸친 언어적 정보를 포함하는 다양한 말뭉치에 대해 사전학습을 진행하여 중요한 일반지식과 질답, 의미유사성 평가, 함의 확인, 문서분류 등의 과제에서 성공적으로 전이되는 장거리 의존성을 처리하는 능력을 학습하여 12개 중 9개의 과제에 대해 state-of-the-art를 달성하였다. 특정 과제에 대한 성능을 높이는 비지도 사전학습은 기계학습연구의 중요한 목표가 되었다.
이 연구는 상당한 성능향상이 정말로 가능하며 어떤 모델(Transformers)과 dataset(장거리 의존성을 포함하는 텍스트)가 이 접근법에 가장 좋은지에 대한 조언을 제공한다. 이 연구가 자연어이해와 다른 분야에 대한 비지도학습에 대한 새로운 연구에 도움이 되기를 희망하며, 나아기 비지도학습이 언제 그리고 어떻게 작동하는지에 대한 우리의 이해를 증진시키기를 바란다.

Refenrences

논문 참조. 71개의 레퍼런스가 있다.

부록은 없다(yeah).

이 글에서는 2018년 2월 Matthew E. Peters 등이 발표한 Deep contextualized word representations를 살펴보도록 한다.

참고로 이 논문의 제목에는 ELMo라는 이름이 들어가 있지 않은데, 이 논문에서 제안하는 모델의 이름이 ELMo이다.
Section 3에서 나오는 이 모델은 Embeddings from Language Models이다.

중요한 부분만 적을 예정이므로 전체가 궁금하면 원 논문을 찾아 읽어보면 된다.

ELMo - Deep contextualized word representations

논문 링크: Deep contextualized word representations

홈페이지: OpenAI Blog

초록(Abstract)

이 논문에서는 단어 사용의 복잡한 특성(문법 및 의미)과 이들이 언어적 문맥에서 어떻게 사용되는지(다의성)를 모델링하는, 새로운 종류의 문맥과 깊게 연관된 단어표현(Deep contextualized word representation)을 소개한다. 이 논문에서의 word vector는 큰 말뭉치에서 학습된 deep bidirectional language model(biLM)의 내부 상태로부터 학습한다. 이 표현(representation)은 이미 존재하는 모델에 쉽게 불일 수 있으며 이로써 QA 등 6개의 도전적인 NLP 문제에서 상당히 향상된 state-of-the-art 결과를 얻을 수 있음을 보였다. 또한 기학습된(pre-trained) 네트워크의 깊은 내부를 살펴보는 분석도 보인다.

1. 서론(Introduction)

기학습된 단어 표현(Pre-trained word representations)은 많은 자연어이해 모델에서 중요한 요소였다. 그러나 문법, 의미, 다의성을 학습한 높은 품질의 representation을 얻는 것은 어려운 일이다. 이 논문에서는 쉽게 다른 모델에 적용가능하며 성능도 뛰어난 Deep contextualized word representation을 소개한다.

이 representation은 (문장 내) 각 token이 전체 입력 sequence의 함수인 representation를 할당받는다는 점에서 전통적인 단어 embedding과 다르다. 이를 위해 이어붙여진 language model(LM)로 학습된 bidirectional LSTM(biLM)로부터 얻은 vector를 사용한다. 이 때문에 이를 ELMo(Embeddings from Language Models) representation이라 부른다. 이는 LSTM layer의 최종 layer만을 취한 것이 아닌, 각 layer 결과를 가중합하여 얻어지며 이것이 성능이 더 좋다.
LSTM의 낮은 단계의 layer(입력과 가까운 층)는 품사 등 문법 정보를, 높은 단계의 layer(출력과 가까운 층)는 문맥 정보를 학습하는 경향이 있다.

많은 실험에서 ELMo representation이 매우 뛰어남을 보여 주었는데, 상대적으로 에러율을 20% 줄이기도 하였다.

2. 관련 연구(Related work)

기학습된 단어 벡터(pretrained word vectors)는 많은 NLP 모델에서 매우 중요한 역할을 했다. 그러나 미리 학습된 단어 벡터는 다의어도 한 개의 벡터로 표현하기 때문에 문맥 정보를 고려하지 못한다.
이를 극복하기 위한 방안으로 보조단어 정보를 활용하거나 각 단어당 여러 벡터를 만드는 방법이 고려되었다. 이 논문의 방법(ELMo representation)은 보조정보로부터의 이점을 가지며 또한 명시적으로 여러 벡터를 만들 필요도 없다.

문맥의존 표현을 학습하는 다른 연구로는 다음이 있다.

• 양방향 LSTM을 사용하는 context2vec(Melamud et al., 2016)
• 표현 안에 pivot word 자체를 포함하는 CoVe(McCann et al., 2017)

Deep biRNN의 낮은 단계의 layer를 사용하여 dependency parsing(Hashimoto et al., 2017)이나 CCG super tagging(Søgaard and Goldbert, 2016) 등의 문제에서 성능 향상을 시킨 연구도 있었다.
Dai and Le(2015)와 Ramachandran et al.(2017)에서는 언어모델(LM)로 인코더-디코더 쌍을 기학습시키고 특정 task에 fine-tune시켰다.

이 논문에서는 미분류된 데이터로부터 biLM을 기학습시킨 후 weights를 고정시키고 task-specific한 부분을 추가하여 leverage를 증가시키고 풍부한 biLM representation을 얻을 수 있게 하였다.

3. ELMo: Embeddings from Language Models

다른 단어 embedding과는 다르게 ELMo word representation은 전체 입력 sequence의 함수이다. 이는 글자수준 합성곱(character convolutions, Sec. 3.1)로부터 얻은 biLM의 가장 위 2개의 layer의 선형함수(가중합, Sec. 3.2)으로 계산된다. 이는 준지도학습과 더불어 biLM이 대규모에서 기학습되며(Sec 3.4) 쉽게 다른 NLP 모델에 붙일 수 있도록(Sec 3.3) 해준다.

3.1. Bidirectional language models

$N$개의 token $(t_1, t_2, …, t_N)$이 있을 때, 전방언어모델(forward language model)은 $(t_1, …, t_{k-1})$이 주어졌을 때 token $t_k$가 나올 확률을 계산한다:

[p(t_1, t_2, …, t_N) = \prod_{k=1}^N p(t_k \vert t_1, t_2, …, t_{k-1})]

최신 언어모델은 token embedding이나 문자단위 CNN을 통해 문맥-독립적 token representation $x_k^{NM}$을 계산하고 이를 전방 LSTM의 $L$개의 layer에 전달한다.
각 위치 $k$에서, 각 LSTM layer는 문맥-의존적 representation $\overrightarrow{h}_{k, j}^{LM}(j = 1, …, L)$을 출력한다.

LSTM의 최상위 layer LSTM 출력 $\overrightarrow{h}_{k, L}^{LM}$은 Softmax layer와 함께 다음 token을 예측하는 데 사용된다.

후방(backward) LSTM은 거의 비슷하지만 방향이 반대라는 것이 다르다. 식의 형태는 똑같지만 뒤쪽 token을 사용해 확률을 계산하고 token을 예측한다.

[p(t_1, t_2, …, t_N) = \prod_{k=1}^N p(t_k \vert t_{k+1}, t_{k+2}, …, t_N)]

즉 $(t_{k+1}, …, t_N)$이 주어졌을 때 representation $\overleftarrow{h}_{k, j}^{LM}$을 계산한다.

biLM은 이 둘을 결합시킨 로그우도를 최대화한다.

[\sum_{k=1}^N \Big( \log \ p(t_k \vert t_1, …, t_{k-1}; \Theta_x, \overrightarrow{\Theta}{LSTM}, \Theta_s) + \log \ p(t_k \vert t{k+1}, …, t_N; \Theta_x, \overleftarrow{\Theta}_{LSTM}, \Theta_s) \Big)]

$\Theta_x$는 token representation, $\Theta_s$는 Softmax layer이며 이 둘은 LSTM의 parameter과는 다르게 고정된다.

3.2. ELMo

ELMo는 biLM의 중간 layer representation을 task-specific하게 결합한다. biLM의 $L$개의 layer는 각 token $t_k$당 $2L+1$개의 representation을 계산한다.

각 biLSTM layer에서

[h_{k, 0}^{LM}: \text{token layer}, h_{k, j}^{LM} = [\overrightarrow{h}{k, j}^{LM}; \overleftarrow{h}{k, j}^{LM}]]

일 때

[R_k = { x_k^{LM}, \overrightarrow{h}{k, j}^{LM}, \overleftarrow{h}{k, j}^{LM} \vert j = 1, …, L } = { h_{k, j}^{LM} \vert j = 0, …, L }]

위의 식은 위치 $k$에서 $R_k$는 $1+L+L=2L+1$개의 representation으로 이루어져 있다는 뜻이다.

Downstream model로의 포함을 위해, ELMo는 $R$의 모든 layer를 하나의 벡터 $\text{ELMo}_k = E(R_k; \Theta_e)$로 압축시킨다.

가장 단순한 예로 ELMo가 단지 최상위 레이어를 택하는 $E(R_k) = h_{k, L}^{LM}$는 TagLM이나 CoVe의 것과 비슷하다.

더 일반적으로, 모든 biLM layer의 task-specific한 weighting을 계산한다:

[\text{ELMo}k^{task} = E(R_k; \Theta^{task}) = \gamma^{task} \sum{j=0}^L s_j^{task} h_{k, j}^{LM}]

$s^{task}$는 softmax-정규화된 가중치이고 scalar parameter $\gamma^{task}$는 전체 ELMo 벡터의 크기를 조절하는 역할을 한다. $\gamma$는 최적화 단계에서 중요하다.
각 biLM layer에서의 활성함수는 다른 분포를 갖는데, 경우에 따라 가중치를 정하기 전 각 biLM layer에 정규화를 적용하는 데 도움이 되기도 한다.

3.3. Using biLMs for supervised NLP tasks

목표 NLP task에 대한 기학습된 biLM과 지도(supervised) 모델구성이 주어지면, 해당 task 모델을 향상시키도록 biLM을 쓰는 과정은 간단하다.

• 단지 biLM을 돌리고 각 단어마다 모든 layer representation을 기록한다.
• 그리고 모델이 이 representation들의 선형결합을 배우도록 한다.
  • 먼저 biLM이 없는 지도 모델을 고려한다.
  • 대부분의 NLP 지도 모델은 가장 낮은 단계의 layer에서 공통구조를 공유하는데, 이는 ELMo를 일관된 방법으로 추가할 수 있게 해 준다.
  • $(t_1, t_2, …, t_N)$이 주어지면 기학습된 단어 embedding(+글자기반 representation)을 사용하여 각 token 위치마다 문맥-독립적 token representation $x_k$를 만든다.
  • 그러면 모델은 biRNN이든 CNN이든 FFN이든 사용하여 문맥-의존적 representation $h_k$를 생성한다.

ELMo를 지도 모델에 추가하려면

• 먼저 biLM의 weight를 고정시키고
• ELMo 벡터 $\text{ELMo}_k^{task}$와 $x_k$를 이어붙인 후
• ELMo enhanced representation $[x_k; \text{ELMo}_k^{task}]$를 task RNN에 전달한다.

SNLI, SQuAD 등의 task에서는 $h_k$를 $[x_k; \text{ELMo}_k^{task}]$로 대체하면 성능이 더 향상되었다.
또한 ELMo에 dropout을 적용하는 것과, $\lambda \Vert w \Vert_2^2$를 loss에 더해 ELMo weight를 정규화하는 것이 ELMo weight에 inductive bias를 유도하여 모든 biLM layer의 평균에 더 가까워지도록 하여 성능에 도움을 주는 것을 발견하였다.

3.4. Pre-trained bidirectional language model architecture

기학습된 biLM은 이전 모델(Józefowicz et al. 2016)의 것과 비슷하지만 양방향 학습의 동시학습을 가능하게 하고 LSTM layer 사이에 residual connection을 추가하였다.

완전히 문자기반인 입력 representation을 유지하면서도 모델복잡도와 계산요구량의 균형을 맞추기 위해, embedding과 은닉차원을 반으로 줄였다.
최종 모델은 4096개의 unit과 512차원의 projection layer, 1-2번 layer 사이 residual connection을 갖는 $L=2$ biLSTM을 사용한다.
그 결과 biLM은 각 입력 token마다 순수 문자기반 입력 때문에 학습셋을 벗어나는 것을 포함한, 3개의 layer of representation을 생성한다. 이는 전통적인 단어 embedding이 고정된 단어사전 하에서 token에 대해 단 한개의 layer of representation을 생성하는 것과 대비된다.

1B word Benchmark로 10 epoch만큼 학습시킨 결과 perplexity가 30.0에서 39.7로 크게 늘었다.

일단 기학습된 biLM은 어떤 task에서도 representation을 계산할 수 있다. 대부분의 downstream task에서는 fine-tuned biLM을 사용하였다.

4. 평가(Evaluation)

6개의 NLP task에서 에러율을 상대적으로 6~20%만큼 줄였다.

Question Answering 부문에선 SQuAD, Textual Entailment에서는 SNLI 데이터셋을 사용했으며, Semantic role labeling, Coreference resolution, Named entity extraction, Sentiment analysis 등의 task에서도 높은 점수를 기록했음을 볼 수 있다.
데이터셋과 어떤 향상이 있었는지에 대한 정보는 원문을 찾아보면 된다.

5. 분석(Analysis)

이 섹션에서는 특정 부분을 빼거나 교체해서 해당 부분의 역할을 알아보는 ablation 분석을 수행한다.

5.1. Alternate layer weighting schemes

biLM layer를 결합시키는 방법은 매우 다양하다. 또한 정규화 parameter $\lambda$도 매우 중요한 역할을하는데, $\lambda$가 크면(e.g., $\lambda=1$) 가중함수를 단순평균함수로 만들고, 작으면(e.g., $\lambda=0.001$) layer 가중치를 서로 달라지게 한다.

[\text{ELMo}k^{task} = E(R_k; \Theta^{task}) = \gamma^{task} \sum{j=0}^L s_j^{task} h_{k, j}^{LM}]

위 결과에서 보듯이 단지 마지막 layer만 쓰는 것보다 모든 layer를 쓰는 것이 더 좋으며, 각각을 단순평균하는 것이 아닌 가중합을 하였을 때(이는 $\lambda$가 작은 것으로 구현됨) 더 성능이 좋아지는 것을 볼 수 있다.
즉 작은 $\lambda$가 ELMo에 도움이 되며 task의 종류에는 크게 영향받지 않는 것 같다.

5.2. Where to include ELMo?

이 논문에서는 단어 embedding을 biRNN의 최하층에만 넣었지만 일부 task에서는 biRNN의 출력에 ELMo를 포함시키는 것이 성능향상을 가져오는 것을 볼 수 있다.

단 위에서 보듯이 모든 경우에 좋은 것은 아니다. SQuAD와 SNLI 모델구성은 biRNN 뒤에 attention layer을 사용하므로 이 layer에 ELMo를 추가하는 것은 biLM의 내부 representatino에 직접 접근할 수 있도록 해 주며 SRL의 경우 task-specific한 문맥 representation이 더 중요하기 때문이라는 설명이 가능하다.

5.3. What information is captured by the biLM’s representations?

ELMo를 추가하는 것만으로 단어 벡터만 있을 때보다 성능이 향상되었기 때문에, biLM의 문맥적 representation은 단어 벡터가 잡아내지 못한 어떤 정보를 갖고 있어야 한다. 직관적으로 biLM은 다의어를 명확화(disambiguation, 다의어의 여러 뜻 중 어떤 의미로 쓰였는지 알아내는 것)한 정보를 갖고 있어야 한다.

위 표에서 GloVe 단어벡터에서 ‘play’ 와 비슷한 단어는 품사를 변형한 것 또는 스포츠에 관한 것만 유사 단어로 뜬다.
그러나 biLM에서는 ‘play’이 비슷한 의미로 쓰인 문장을 유사한 것으로 판단할 수 있음을 알 수 있다.

Word sense disambiguation

단어 의미 명확화에서 충분히 괜찮은 성능을 보여준다.

POS tagging

품사 태깅도 꽤 잘 한다고 한다.

Implications for supervised tasks

이러한 실험들은 왜 biLM에서 모든 layer가 중요한지를 알려 준다. 각 layer마다 잡아낼 수 있는 문맥정보가 다르기 때문이다.

5.4. Sample efficiency

ELMo를 추가했을 때는 그렇지 않을 때보다 학습속도도 빠르며(최대 49배 정도) 학습데이터가 적을 때도 훨씬 효율적으로 학습한다.

5.5. Visualization of learned weights

입력 layer에서 task 모델은, 특히 corefenrece와 SQuAD에서 첫번째 biLSTM layer를 선호한다. 출력 layer에서 낮은 레이어에 조금 더 중점을 두지만 상대적으로 균형잡힌 모습을 보여준다.

6. 결론(Conclusion)

이 논문에서는 biLM으로부터 고품질의 깊은 문맥의존 representation을 학습하는 일반적인 방법을 소개했으며, 넓은 범위의 NLP 문제들에서 ELMo를 적용했을 때 많은 성능 향상을 가져오는 것을 보였다. 또한 ablation을 통해 biLM의 모든 layer들이 각각 효율적으로 문맥 정보를 포착하여, 이를 모두 사용하는 것이 좋다는 것을 보였다.

Refenrences

논문 참조. 레퍼런스가 많다.

또한 이 논문이 일부 모듈의 원형으로 삼은 모델들의 구조를 살펴볼 수 있다.

Appendix

부록에서는 $\gamma$의 중요성이나, 각 NLP task에서 ELMo를 붙였을 때 성능 향상이 이루어지는 예시들을 많이 들고 있다. 한번쯤 살펴보자.

이 글에서는 2017년 6월(v1) Ashish Vaswani 등이 발표한 Attention Is All You Need를 살펴보도록 한다.

중요한 부분만 적을 예정이므로 전체가 궁금하면 원 논문을 찾아 읽어보면 된다.

Attention Is All You Need

논문 링크: Attention Is All You Need

Pytorch code: Harvard NLP

초록(Abstract)

성능 좋은 변환(번역) 모델은 인코더와 디코더를 포함한 복잡한 recurrent 또는 convolutional 신경망에 기반을 두고 있다. 최고 성능을 내는 모델 역시 attention mechanism을 사용하여 인코더와 디코더를 연결한다.
이 논문에서 recurrence와 convolution을 전부 제외하고 오직 attention mechanism에만 기반한 Transformer라는 간단한 모델을 제안한다. 두 기계번역 task 실험에서는 이 모델은 병렬화와 학습시간 감소와 더불어 최고 수준의 품질을 가진다는 것을 보여준다. 이 모델은 WMT 2014 영어$\rightarrow$독일어 번역 task에서 이전보다 2 높은 28.4 BLEU를 달성하였다. 여기서 이 모델은 8개의 GPU로 8일 동안 학습시켜 41.8점의 BLEU state-of-the-art 단일 모델이다.
이 논문에서 Transformer는 크거나 한정된 학습 데이터를 가지고서도 성공적으로 다른 task들에 일반화될 수 있음을 보인다.

1. 서론(Introduction)

RNN, LSTM, GRU 등은 sequence 모델링과 언어모델 등 변환 문제, 기계번역 등의 문제에서 뛰어난 성과를 보였다.
Recurrent 모델은 보통 입력과 출력의 symbol position에 따라 계산을 수행한다. 계산 단계에서 위치를 적절히 맞추기 위해 이전 상태 $h_{t-1}$과 위치 $t$의 함수인 은닉상태 $h_t$를 생성한다. 이는 근본적으로 메모리 제한으로 인해 sequence가 길수록 병렬화를 힘들게 한다. 최근 들어 모델의 성능 자체는 비약적으로 상승했지만 위의 문제는 여전히 남아 있다.

Attention mechanism은 입력과 출력 sequence의 거리에 상관없이 의존성을 모델링함으로써 다양한 과제에서의 sequence 모델링과 변환 모델에서 매우 중요한 부분이 되었다. 그러나 거의 대부분의 경우 recurrent 네트워크와 함께 사용되고 있다.

이 논문에서는, Transformer라는, recurrence를 제거하고 입력-출력 간 전역 의존성을 학습할 수 있는 attention mechanism만을 사용한 모델 구조를 제안한다. Transformer는 병렬화를 비약적으로 달성하였으며 8개의 P100 GPU만으로 딱 12시간만을 학습하여 state-of-the-art 결과를 얻을 수 있게 한다.

2. 배경(Background)

연속적 계산을 줄이려는 노력은 Extended Neural GPU, ByteNet, ConvS2S 등의 모델을 탄생시켰으나 이들은 전부 CNN을 기본 블록으로 사용한다. 이러한 모델들은 임의의 위치의 input-output 사이의 관련성을 파악하기 위해서는 거리에 따라(선형 또는 로그 비례) 계산량이 증가하며, 이는 장거리 의존성을 학습하기 어렵게 한다.
Transformer는, 이를 상수 시간의 계산만으로 가능하게 하였다.

intra-attention으로도 불리는 Self-attention은 sequence의 representation을 계산하기 위한 단일 sequence의 다른 위치를 연관시키는 attention mechanism이다. Self-attention은 많은 과제들에서 사용되었으며 성공적이었다.

End-to-end 메모리 네트워크는 sequence-aligned recurrence 대신 recurrent attention mechanism에 기반하였으며 simple-language QA와 언어모델링 task 등에서 좋은 성과를 내었다.

그러나, Transformer는 RNN이나 convolution 없이 오직 attention에 전적으로 의존한 첫 번째 변환 모델이다. 앞으로 이 모델에 대한 설명이 이어질 것이다.

3. 모델 구성(Model Architecture)

Transformer는 크게 인코더와 디코더로 나뉘며, 인코더는 입력인 symbol representations $(x_1, …, x_n)$을 continuous representations $z = (z_1, …, z_n)$으로 매핑한다. $z$가 주어지면, 디코더는 한번에 한 원소씩 출력 sequence $(y_1, …, y_n)$를 생성한다.
각 단계는 자동회귀(auto-regressive)이며, 다음 단계의 symbol을 생성할 때 이전 단계에서 생성된 symbol을 추가 입력으로 받는다.

Transformer는 인코더와 디코더 모두에서 쌓은 self-attention과 point-wise FC layer를 사용하며, 그 구성은 아래 그림에 나타나 있다.

3.1. Encoder and Decoder Stacks

인코더는 $N = 6$ 개의 동일한 레이어로 구성되며, 각 레이어는 아래 두 개의 sub-layer로 이루어져 있다.

• multi-head self-attention mechanism
• simple, position-wise fully connected feed-forward network

각 sub-layer의 출력값은 LayerNorm($x$ + Sublayer($x$))이고, Sublayer($x$)는 sub-layer 자체로 구현되는 함수이다. 이 residual connection을 용이하게 하기 위해, embedding layer를 포함한 모델의 모든 sub-layer는 $d_{model} = 512$차원의 출력값을 가진다.

디코더 역시 $N = 6$ 개의 동일한 레이어로 구성되지만, 각 레이어는 인코더의 것과 동일한 두 개의 sub-layer 외에 한 가지를 더 가진다.

• encoder stack의 출력값에 multi-head attention을 수행하는 sub-layer

인코더와 비슷하게 residual connection이 각 sub-layer의 정규화 layer 뒤에 있다. 그리고 디코더가 출력을 생성할 때 다음 출력에서 정보를 얻는 것을 방지하기 위해 masking을 사용한다. 이는 $i$번째 원소를 생성할 때는 $1 \sim i-1$번째 원소만 참조할 수 있도록 하는 것이다.

3.2. Attention

Attention 함수는 query + key-value $\rightarrow$ output 으로의 변환을 수행한다. query, key, value, output은 모두 벡터이다. output은 value들의 가중합으로 계산되며, 그 가중치는 query와 연관된 key의 호환성 함수(compatibility function)에 의해 계산된다.

3.2.1. Scaled Dot-Product Attention

이 이름은 Attention을 계산하는데 dot-product를 쓰고, 그 결과에 scale 조정을 하기 때문에 이렇게 붙여졌다.

입력은 $d_k$차원의 query와 key, $d_v$차원의 value로 구성된다.
query와 모든 key의 내적(dot product)을 계산하고, 각각 $\sqrt{d_k}$로 나누고, value의 가중치를 얻기 위해 softmax 함수를 적용한다.

실제로는, query들에 대해 동시에 계산하기 위해 이를 행렬 $Q$로 묶는다. 모든 key와 value 역시 각각 행렬 $K$와 $V$로 표현된다. 이제 $Q, K, V$의 attention을 구하는 식은 다음과 같다.

[Attention(Q, K, V) = \text{softmax} \Big( \frac{QK^T}{\sqrt{d_k}} \Big) V]

가장 널리 쓰이는 attention 함수는 다음 두 가지다:

• Additive attention: 단일 hidden layer의 feed-forward 네트워크를 사용하여 호환성 함수를 계산한다. $d_k$가 작을 때 성능이 더 좋다.
• Dot-product attention: $d_k$가 더 클 때는 빠른 행렬곱 알고리즘에 힘입어 더 빠르고 더 공간 효율적이다.

3.2.2. Multi-Head Attention

$d_{model}$차원 key, value, query로 단일 attention function을 쓰는 것보다 query, key, value를 각각 $d_k, d_k, d_v$차원으로 각각 다르게 $h$번 학습시키는 것이 낫다. 여기서 $h$번 학습시킨다는 것은 단지 반복을 한다는 것이 아니라, 각 sub-layer에 동일한 부분이 $h$개 존재한다는 뜻이다. 위 그림의 오른쪽을 보자.
이렇게 각각 따로 계산된 $h$쌍의 $d_v$차원 출력은 이어붙인(concatenate) 후 한번 더 선형 함수에 통과시켜(projected) 최종 출력값이 된다.

식으로 나타내면 다음과 같다.

[\text{MultiHead}(Q, K, V) = \text{Concat}(head_1, …, head_h)W^O, where \ head_i=\text{Attention}(QW_i^Q, KW_i^K, VW_i^V)]

여기서 $ W_i^Q \in \mathbb{R}^{d_{model} \times d_k}, W_i^K \in \mathbb{R}^{d_{model} \times d_k}, W_i^V \in \mathbb{R}^{d_{model} \times d_v}, W^O \in \mathbb{R}^{hd_v \times d_{model}} $이며, 논문에서는 $h=8, d_k=d_v=d_{model}/h = 64$를 사용하였다.
각 head의 차원이 줄었기 때문에 단일 head attention과 계산량은 비슷하다.

3.2.3. Applications of Attention in our Model

• “encoder-decoder attention” layer에서, query는 이전 디코더 layer에서 오며 memory key와 value는 encoder의 출력에서 온다. 이는 디코더가 입력의 모든 위치(원소)를 고려할 수 있도록 한다.
• 인코더는 self-attention layer를 포함한다. 여기서 모든 key, value, query는 같은 곳(인코더의 이전 layer의 출력)에서 온다. 따라서 인코더의 각 원소는 이전 layer의 모든 원소를 고려할 수 있다.
• 이는 디코더에서도 비슷하다. 그러나 auto-regressive 속성을 보존하기 위해 디코더는 출력을 생성할 시 다음 출력을 고려해서는 안 된다. 즉 이전에 설명한 masking을 통해 이전 원소는 참조할 수 없도록 한다. 이 masking은 dot-product를 수행할 때 $-\infty$로 설정함으로써 masking out시킨다. 이렇게 설정되면 softmax를 통과할 때 0이 되므로 masking의 목적이 달성된다.

3.3. Position-wise Feed-Forward Networks

인코더와 디코더의 각 layer는 FC feed-forward 네트워크를 포함하는데, 이는 각 위치마다 동일하게 적용되지만 각각 따로 적용된다. 이는 ReLU 활성함수와 2개의 선형변환을 포함한다. kernel size가 1인 CNN과 같다.

[\text{FFN}(x) = \max(0, xW_1 + b_1)W_2 + b_2]

각 레이어에 이 부분은 독립적인 parameter를 사용한다. 논문에서는 $d_{model}=512, d_{ff} = 2048$을 사용했다.

3.4. Embeddings and Softmax

다른 모델들과 비슷하게 embedding을 사용하였다. 이 모델에서는 2개의 embedding layer와 pre-softmax 선형변환 사이에 같은 weight 행렬을 사용했다. Embedding layer에는 $\sqrt{d_{model}}$을 곱한다.

3.5. Positional Encoding

이 모델에는 recurrence도 convolution도 사용되지 않기 때문에 sequence에 있는 원소들의 위치에 대한 정보를 따로 넣어 주어야 한다. 그래서 인코더와 디코더 stack의 밑부분에 positional encodings를 입력 embedding에 추가하였다. 이는 embedding과 갈은 $d_{model}$차원을 가지며, 따라서 더할 수 있다. 모델에서 사용된 것은 사인/코사인 함수이다.

[\quad PE_{(pos, 2i)} = sin(pos/10000^{2i/d_{model}})]

[\ PE_{(pos, 2i+1)} = cos(pos/10000^{2i/d_{model}})]

$pos$는 위치(position)이고 $i$는 차원이다.

가능한 여러 함수 중 사인함수 버전을 선택한 이유는 학습 때보다 더 긴 sequence를 만나도 추정이 가능하기 때문이다.

4. 왜 Self-Attention인가(Why Self-Attention)

$(x_1, …, x_n) \rightarrow (z_1, …, z_n)$에 self-attention이 적합한 이유는

1. layer 당 전체 계산량이 적고
2. 계산이 병렬화될 수 있다. 즉 병렬적으로 한번에 많은 계산을 할 수 있는데, recurrence의 경우 순차적으로 계산해야 하기 때문에 계산의 병렬화가 거의 불가능하다.
3. 장거리 의존성(long-range 또는 long-term dependency) 때문이다.

장거리 의존성을 학습할 수 있는 중요 요인은 네트워크 상에서 횡단할 수 있는 경로의 길이인데, 길이가 짧을 때는 다 비슷하므로 최대 길이를 중점적으로 살펴보았다.

위 표에서 볼 수 있듯 장거리 의존성의 학습 속도(또는 능력)에서 self-attention이 가장 좋다.

5. 학습(Training)

6. 결과(Results)

Machine Translation, Model Variations, English Constituency Parsing에 대한 실험 결과이다. Base Model만 해도 충분히 최고 성능을 보여주며, 특히 Big Model의 경우 state-of-the-art를 상당한 수준으로 경신하는 성능을 보여 주었다.
이외에 따로 요약이 필요하지는 않아 자세한 조건이나 성능, 설명은 생략하도록 하겠다. 필요하면 논문 참조하는 편이 낫다.

결과: 부록

원래는 부록에 있는 자료이지만 결과 섹션으로 가져왔다.

아래 그림에서는 making 이라는 단어가 making…more difficult 라는 구를 만드는 데 중요한 역할을 하는 것을 보여준다.

여러 개의 attention을 시각화한 자료는 다음 두 그림에서 확인할 수 있다.

7. 결론(Conclusion)

(여러 번 나온 말이지만) Transformer는 recurrence와 convolution을 모두 제거한, 오직 attention에만 의존하는 새로운 종류의 모델이다. 이 모델은 계산량을 줄이고 병렬화를 적용해 학습 속도가 훨씬 빠를 뿐만 아니라 그 성능 또한 state-of-the-art를 달성하는 수준에 이르렀다.
또한 이러한 attention에 기반한 모델은 다른 task들에 적용할 수도 있다. 비단 텍스트뿐만 아니라 이미지, 오디오나 비디오 등의 상대적으로 큰 입력-출력을 요하는 task들에 효과적으로 사용할 수 있을 것이다.

이 모델을 학습하고 평가한 코드는 여기에서 찾아볼 수 있다.

Refenrences

논문 참조. 40개의 레퍼런스가 있다.

이 글에서는 2013년 8월(v1) Alex Graves가 발표한 Generating Sequences With Recurrent Neural Networks를 살펴보도록 한다.

연구자의 홈페이지도 있다.

중요한 부분만 적을 예정이므로 전체가 궁금하면 원 논문을 찾아 읽어보면 된다.

Generating Sequences With Recurrent Neural Networks

논문 링크: Generating Sequences With Recurrent Neural Networks

초록(Abstract)

이 논문은 LSTM(Long Short-term Memory) RNNs이 어떻게 넓은 범위의 구조를 가진 복잡한 시퀀스(sequences, 문장 등)를 만들 수 있는지(= 단순히 어느 시점에 하나의 부분만 예측하는 방법)를 보여준다. 이 접근법은 텍스트(이산값)와 손글씨(실수값)에 의해 보여질 것이다. 그리고 네트워크가 텍스트 문장에 대해 예측을 수행함으로써 손글씨 합성으로까지 확장한다. 이 결과 시스템은 다양한 스타일의 정말 실제 같은 필기체를 생성할 수 있다.

1. 서론(Introduction)

RNNs(Recurrent Neural Networks)은 음악, 텍스트, 모션캡쳐 데이터 등과 같은 연속데이터를 생성하기 위해 사용되는 모델이다. RNN은 일반적으로 지금까지의 입력값과 모델 내부 parameter를 바탕으로 바로 다음 것이 무엇일지를 예측하는 모델이다.
RNN은 많은 경우 그 예측이 애매하며 불확실하다(fuzzy). 그 이유는 항상 확정적이며 똑같은 결과만을 내놓는다면 생성되는 문장이나 음악은 항상 똑같을 것인데 우리는 그런 것을 원하지 않으며, 또한 확률적인(stochastic) 방법이 정확한(exact) 일치 방법에 비해 차원의 저주(the curse of dimensionality)를 피하기 적합하며 그로 인해 시퀀스 또는 다변수 데이터를 모델링하는 데 더 뛰어나다.

이론적으로는 충분히 큰 RNN은 어떤 복잡한 시퀀스(sequences)도 생성할 수 있어야 한다. 그러나 Vanilla RNN은 최근 몇 개의 입력값을 기억하며 이에 의존할 뿐 멀리 떨어진 이전 또는 장기적인 정보를 거의 기억하지 못한다.
이를 많은 부분 해결한 것이 바로 LSTM이다. 이 역시 기본적으로는 이전 정보를 기억하는 RNN 구조를 따르지만 조금 더 복잡한 구조를 가지며 장기적(long-range) 정보를 저장하는 데 뛰어난 능력을 보인다.

이 논문에서는 다음과 같은 것들을 다룰 것이다.

• Section 2: LSTM을 여럿 쌓을 ‘deep RNN’을 정의하고 어떻게 다음 단계를 예측하는 데 필요한 학습을 진행하며 시퀀스를 생성하는지 보여준다.
• Section 3: Penn Treebank와 Hutter Prize Wikipedia 데이터셋에 대해 예측을 수행하고 state-of-the-art 수준임을 보인다.
• Section 4: mixture density output layer를 사용하여 어떻게 실제 데이터에 적용할 수 있는지와 IAM Online Handwriting Database에 대한 실험 결과를 보인다.
• Section 5: 예측 네트워크를 짧은 주석에 기반하도록 하여 확장시켜서 어떻게 손글씨 합성을 시킬 수 있는지를 보인다.
• Section 6: 결론과 함께 추후 연구 방향을 제시한다.

2. 예측 네트워크(Prediction Network)

위 그림은 이 논문에서 사용된 기본 RNN 모델의 구조이다. 입력값 $x = (x_1, …, x_T)$은 $N$층에 걸쳐 쌓인 재귀적으로 연결된 hidden layers를 통과하며 $h^n = (h_1^n, …, h_T^n)$ 를 계산하고 최종적으로 $N$층을 다 통과하면 출력벡터 시퀀스 $y = (y_1, …, y_T)$를 얻는다. 각 출력벡버 $y_t$는 가능한 다음 입력값 $x_{t+1}$에 대한 예측분포 $P(x_{t+1} \vert y_t)$를 뜻한다. 초기값 $x_1$은 언제나 null 벡터이다.

입력과 모든 hidden layer, 그리고 모든 hidden layer와 출력과 ‘skip-connections’이 존재함을 기억하라. 이는 vanishing gradient 문제를 피해 깊은 신경망(DNN)을 학습시키기 용이하게 한다. $N=1$인 경우에 vanilla RNN과 같음을 확인할 수 있다.

Hidden layer의 각 활성값은 $t=1…T, n=2…N$ 동안 반복적으로 계산된다:

[h_t^1 = \mathcal{H}(W_{ih^1x_t} + W_{h^1h^1}h^1_{t-1} + b^1_h)]

[h_t^n = \mathcal{H}(W_{ih^nx_t} + W_{h^{n-1}h^n}h^{n-1}{t} + W{h^nh^n}h^n_{t-1} + b^n_h)]

$W$는 각 레이어의 가중치 행렬이다. 은닉 시퀀스가 주어졌을 때, 출력 시퀀스는

[\hat{y_t} = b_y + \sum^N_{n=1} W_{h^n y h_t^n}]

[y_t = \mathcal{Y}(\hat{y_t})]

$\mathcal{Y}$는 출력레이어 함수이다.

입력시퀀스 $x$에 대해 예측분포와 시퀀스 손실함수는

[Pr(x) = \prod_{t=1}^T Pr(x_{t+1} \vert y_t)]

[\mathcal{L}(x) = -\prod_{t=1}^T \log Pr(x_{t+1} \vert y_t)]

로 정의된다.

LSTM의 구조에 대해서는 다른 블로그들에 자세히 잘 설명되어 있으니 참고하자.

3. 문자 예측(Text Prediction)

텍스트 데이터는 이산값이고, 이런 것들은 보통 ‘one-hot’ 방식으로 인코딩된다. 텍스트의 경우 단어(word) 수준으로 인코딩을 수행하게 되고, 이는 벡터의 크기가 단어 사전의 크기(보통 적어도 10만 이상)가 되는 문제가 발생한다.

최근에는 단어 수준 대신 문자 수준으로 예측을 수행하는 방법이 많이 고려되고 있다. 이 방법의 장점은

• 단어 수준 인코딩에 비해 성능이 별로 떨어지지 않으며
• 벡터의 크기가 작고
• 이전에 나타나지 안았던(unknown) 단어에 대한 대비가 필요 없어지며
• 새로운 단어를 만들 가능성도 생긴다.

따라서 이 논문에서는 문자 단위로 생성하는 모델을 고려할 것이다.

3.1. Penn Treebank Experiments

이 데이터셋은 Wall Street Journal corpus의 일부로 네트워크의 예측능력보다는 시퀀스 생성능력에 초점을 두고 실험할 것이다.
Penn Treebank 데이터셋은 100만 단어 정도의 작은 데이터셋이지만 언어 모델링 벤치마크에서 널리 사용된다. 93만 단어의 training set, 7만 4천 단어의 validation set, 8만 2천 단어의 test set을 포함한다. 단어는 1만 종류이며 나머지는 전부 unknown 처리되어 있다.

이 실험은 Penn corpus에 대해 단어 수준과 문자 수준의 LSTM 예측기의 성능을 비교하는 것이다. 두 경우 모두 1000개의 LSTM unit을 사용했고, 단어/문자 수준 벡터의 크기는 다르다(49 vs 10000, 가중치행렬의 크기는 4.3M vs 54M).

SGD(Stochastic Gradient Descent), learning rate 0.0001, momentum 0.99, LSTM derivates는 [-1, 1] 범위로 clip된다.

위 실험의 결과를 두 가지로 요약하면

• 단어 수준 모델이 문자 수준 모델보다 약간 더 성능이 좋다는 것과
• LSTM은 Vanilla RNN보다 훨씬 빠르고 새 데이터에 최적화된다는 것이다.

3.2. Wikipedia Experiments

2006년 Marcus Hutter, Jim Bowery, Matt Mahoney로부터 시작된 영문 위키피디아의 첫 1억(100M) 바이트의 데이터인 Wikipedia data는 다양한 단어와 문자를 포함한다. 아랍어나 중국어 등 비 라틴 알파벳 뿐만 아니라 메타데이터를 지정하는 XML 태그 등 그 종류가 꽤 방대하다.
첫 96M 바이트는 training set, 나머지 4M 바이트는 validation으로 사용된다. 데이터는 205 one-byte 유니코드 기호를 사용한다.

여기서는 더 큰 모델을 사용했다. 700 LSTM unit을 포함하는 7층짜리 네터워크로 가중치행렬의 크기는 21.3M이다. momentum이 0.9인 것을 제외하면 다른 조건은 같다.

Wikipedia는 글의 주제와 같은 수천 단어 이상일 수 있는 넓은 범위(long-range) 의존성을 포함하기 때문에 LSTM의 내부 상태는 매번 100 sequence 만큼만을 리셋한다. 즉 gradient를 근사하는 것인데, 이는 넓은 범위 의존성을 최대한 잃지 않으면서 학습속도를 높이는 방법이다.
아래 결과를 보면 Dynamic evaluation을 사용했을 때 성능이 더 좋게 나온다. 이는 위키피디아의 넓은 범위 일관성 때문인 것으로 보인다(예: 특정 단어들은 특정 글에서 더 빈번히 등장하며, 평가 중에 이에 맞출 수 있는 것이 더 유리하다).

논문에는 실제 위키피디아 페이지와, 예측 네트워크가 생성한 위키피디아 페이지를 보여주고 있는데 그 중 일부를 가져왔다.

보면 은근히 괜찮은 품질의 글을 생성해냈음을 볼 수 있다. 특히 봐줄 만한 이름들(Lochroom River, Mughal Ralvaldens, swalloped) 등의 모델이 직접 생성해낸 이름들이 눈의 띈다.

괄호나 따옴표를 여닫는 것은 언어 모델의 메모리에 명백히 이를 알려주는 지시자가 있는데, 이는 좁은 범위(short-range)의 문맥으로는 모델링될 수 없어서 중간 글자들만으로는 예측할 수 없기 때문이다. 위 샘플 결과는 괄호나 따옴표의 적절한 수를 지켰을 뿐만 아니라 nested XML tag 등도 잘 구현해 내었다.
네터워크는 비 라틴 문자들, 키릴 문자나 한자, 아랍 문자 등을 생성했고, 이는 영어보다 더 기본적인 모델을 배운 것으로 보인다. 이 경우에도 봐줄 만한 이름들을 생성했다.

4. 손글씨 예측(Handwriting Prediction)

예측 네트워크가 실수값 시퀀스(real-valued sequences)도 충분히 잘 생성할 수 있는지 확인하기 위해 online 손글씨 데이터에 이를 적용해 보았다(online 필기 데이터란 그냥 필기 이미지만 있는 offline 데이터와는 달리 펜으로 해당 필기를 할 때 어떤 궤적을 그렸는지에 대한 정보가 있는 것이다). IAM-OnDB 데이터셋을 사용하였다.
IAM-OnDB 데이터셋은 221명의 사람이 Lancaster-Oslo-Bergen 말뭉치를 쓴 필기 데이터이다.

4.1 혼합밀도 출력값(Mixture Density Outputs)

Mixture Density Outputs의 아이디어는 혼합분포(mixture distribution)을 parameterise하기 위해 신경망의 출력값을 사용하는 것이다. 출력값의 부분집합은 혼합가중치(mixture weights)를 정의하기 위해, 남은 출력값은 독립적인 mixture components를 parameterise하도록 사용된다. Misture weight 출력값은 정규화, softmax 등을 거쳐 의미 있는 범위 안에 포함되도록 한다. 이는 Boltzmann machine이나 다른 무방향 모델과는 달리 density가 정규화되고 직접 미불되며 편향되지 않는 샘플을 고른다는 점에서 대비된다.

손글씨 실험을 위해, 기본적인 RNN 구조는 Section 2에서 변하지 않았다. 각 입력벡터 $x_t$는 이전 입력으로부터의 pen offset을 정의하는 실수쌍 $x_1, x_2$로 구성되며, 벡터가 stroke로 끝나면(다음 벡터가 기록되기 전에 펜이 보드에서 떨어지면) 1, 아니면 0의 값을 갖는 이진값 $x_3$로 구성된다.
이변수 혼합 가우시안(A mixture of bivariate Gaussians)이 $x_1, x_2$를 베르누이 분포가 $x_3$을 예측한다.

각 출력벡터 $y_t$는 stroke로 끝날 확률 $e$, 평균 $\mu^j$, 표준편차 $\sigma^j$, 상관계수 $\rho^j$, $M$ mixture components에 대한 혼합가중치 $\pi^j$로 구성된다.

[x_t \in \mathbb{R} \times \mathbb{R} \times {0, 1}]

[y_t = \Big( e_t, { \pi_t^j, \mu_t^j, \sigma_t^j, \rho_t^j }_{j=1}^M \Big)]

평균과 표준편차는 2차원 벡터이고 나머지는 스칼라이다. 벡터 $y_t$는 네트워크 출력값 $\hat{y}_t$로부터 얻어지며,

[\hat{y}t = \Big( \hat{e}_t, { \hat{w}_t^j, \mu_t^j, \sigma_t^j, \rho_t^j }{j=1}^M \Big) = b_y + \sum_{n=1}^N W_{h^ny}h_t^n]

이다.

이 density map에서 두 종류의 예측을 볼 수 있다:

• 글자를 따라 존재하는 작은 점들(지금 써지고 있는 stroke를 예측)
• 세 개의 큰 원(다음 stroke의 시작점이 되는, stroke의 끝을 예측)

끝획(end-of-stroke)는 더 큰 분산을 갖는데 이는 화이트보드에서 펜이 떨어졌을 때 그 위치가 기록되지 않기 때문이며, 따라서 다음 stroke와의 거리가 커질 수 있다.

아래쪽 열지도는 갈은 sequence에서 misture component weights를 보여준다.

4.2 실험(Experiments)

네트워크는 RMSProp을 사용하였으며 가중치 업데이트 식은 다음과 갈다.

손글씨 예측 결과는 다음과 같다.

5. 손글씨 합성(Handwriting Synthesis)

손글씨 합성은 sequence가 매우 다른 길이를 가질 수 있고 그 사이의 alignment는 데이터가 생성되기 전까지 알려지지 않는다는 점에서 어렵다. 이는 각 글자가 필체, 크기, 펜 속도 등에 따라 매우 달라지기 때문이다.

연속적인 예측을 할 수 있는 한 신경망 모델은 RNN transducer이다. 그러나 이전 연구 결과들은 만족스럽지 못하다.

5.1. 합성 네트워크(Synthesis Network)

네트워크 구조는 다음과 같다.

길이 $U$의 글자 sequence $c$가 주어지고 길이 $T$의 data sequence $x$가 주어졌을 때, 시간 $t(1\le t \le T)$에서 $c$로의 soft window $w_t$는 $K$ Gaussian 함수의 혼합에 의해 정의된다:

[\phi(t, u) = \sum_{k=1}^K \alpha_t^k \text{exp} \Big( - \beta_t^k (\kappa_t^k - u)^2 \Big)]

[w_t = \sum_{u=1}^U \phi(t, u)c_u]

$\phi(t, u)$는 시간 $t$에서 $c_u$의 window weight이고, $\kappa_t$는 window의 위치를 제어하며, $\beta_t$는 window의 너비를, $\alpha_t$는 혼합 내에서 window의 중요도를 제어한다.

5.2. 실험(Experiments)

실험은 이전 section과 동일한 입력 데이터를 사용한다. IAM-OnDB는 이제 글자 sequence $c$를 정의한다.

5.3~5.5 Sampling(Unbiased, Biased, Prime Sampling)

Bias를 다르게 하는 등의 변형을 거쳐 손글씨를 합성한 결과를 몇 개 가져왔다.

Refenrences

논문 참조. 33개의 레퍼런스가 있다.

이 글에서는 2019년 ICML(International Conference on Machine Learning)에서 어떤 논문들이 accept되어 발표되었는지를 알아볼 것이다. 3424개의 논문이 접수되어 774개의 논문만이 구두 및 포스터 발표로 진행되었다.

논문 리스트는 목차와 같다. 774개를 다 살펴볼 수는 없으므로 몇 개만 추려서 최근 동향을 살펴보도록 하자.

Training Neural Networks with Local Error Signals

이 논문은 표현(representation)에 대한 것인데, 논문에 쓰인 표현들이 참 어렵다.

초록을 대략 번역하자면,

풀린 표현(disentangled representation)의 무감독 학습(unsupervised learning)의 핵심 아이디어는 ‘실제 세계의 데이터는 무감독 학습 알고리즘에 의해 복구될 수 있는 몇 가지 설명요인에 의해 생성된다’는 것이다.

이 논문에서, 풀린 표현의 무감독 학습은 모델과 데이터 모두에 대해 귀납적 편향(inductive biases) 없이는 본질적으로 불가능하다는 것을 이론적으로 보일 것이다. 또한 6개의 최신 무감독 풀림 학습(unsupervised disentangled learning) 방법과 풀림 측정방식(disentangled measures)을 구현하여 이를 여러 데이터셋에 대해 12000개 이상의 모델을 학습시킬 것이다.

이로써

• 여러 방법들이 ‘대응되는 loss에 의한’ 성질들을 강제함에도 불구하고 감독 없이는 잘 풀린(well-disentangled) 모델은 식별될 수 없다는 사실과(역자 주: 모델이 식별될 수 없다는 것은 이를테면 두 가지 모델이 생성한 각각의 결과가 있을 때, 그 결과만 보고 원래 모델이 무엇이었을지를 알 수 없다는 뜻이다),
• ‘풀린 정도가 증가한(increased disentanglement)’ 것도 downstream task의 학습의 샘플 복잡도의 감소로 이어지지는 않는다는 것

을 알아내었다.

이같은 결과는 앞으로 풀린 학습에 대한 연구는

• 명백히 귀납적 편향과 감독에 의해야 하며,
• 학습된 표현의 풀림을 강제하는 것의 구체적인 이점을 조사하며,
• 여러 데이터셋을 다룰 수 있는 재현 가능한 실험 설정을 고려해보아야 한다

는 것을 말해준다.

실제 논문 서론에서 주장하는 contribution은,

• 풀린 표현의 무감독 학습은 ‘학습방법과 데이터셋 모두에 대한 귀납적 편향’ 없이는 본질적으로 불가능함을 이론적으로 보인 것
• 현재의 여러 무감독 풀림 학습 방법들을 조사 및 구현하여 이를 여러 데이터셋과 모델을 학습시킨 것
• 풀린 표현을 학습하고 평가하는 disentanglement_lib라는 새로운 라이브러리를 공개한 것
• 상당한 계산량을 필요로 하는 1만 개 이상의 사전 학습된(pre-trained) 모델을 공개한 것
• 무감독 풀림 학습에 대한 여러 생각들을 검증해보았다:
  • 고려된 모든 방법들이 샘플링된 posterior들의 차원(dimensions)의 독립성을 보장한다고 해도, 표현의 차원을 상관관계가 있다.
  • random seed와 hyperparameter이라는 무감독 조건 하에서 고려된 모델들이 풀린 표현을 더 잘 학습한다는 증거가 없다.
  • (데이터셋을 통한 훌륭한(학습이 잘 되는) hyperparameter들을 주는 것을 허용한다 할지라도) ‘ground-truth 레이블에 접근할 수 없는’ 잘 학습된 모델은 식별될 수 없다.
  • 고려된 모델과 데이터셋에 대해, 학습의 샘플 복잡도의 감소와 같은 downstream task에 풀림이 유용하지 않다.
• 실험 결과에 의해, 향후 연구에 대한 세 가지 중요한 부분을 제안하였다: 이는 초록 부분과 같다.

Rates of Convergence for Sparse Variational Gaussian Process Regression

초록

Gaussian process posteriors에 대한 훌륭한 변분 근사법(variational approximations)은 데이터셋 크기 $N$에 대해 $O(N^3)$의 시간이 걸리는 것을 막기 위해 개발되었다. 이 방법은 시간복잡도를 $O(N^3)$에서 $O(NM^2), M \ll N $의 시간으로 줄여 주었다.
$M$은 이 preocess를 요약하는 유도변수(inducing variables)인데, 수행시간은 $N$에 선형 비례함에도 불구하고 실제로는 근사의 품질을 결정하는 $M$이 얼마나 큰지에 실질적인 영향을 더 받는다.
이 논문에서, $N$에 비해 훨씬 느리게 증가하는 어떤 $M$에 대해 높은 확률로 KL divergence를 임의로 작게 만들 수 있음을 보인다. 특히 Square Exponential kernel을 쓰는 D차원의 정규분포 입력에 대한 회귀의 경우 $M = O(log^D N)$이면 충분하다.
이 논문의 결과는 데이터셋이 커질수록 Gaussian process posteriors는 적은 비용으로 근사될 수 있으며, 연속학습 시나리오(continual learning scenarios)에서 $M$을 증가시키는 구체적인 방법을 보이는 것이다.

서론

Gaussian processes(GPs)는 베이지안 모델에서 convenient priors인 함수에 대한 분포이다. 이는 좋은 불확실성 측정을 해내기 때문에 특히 회귀 모델에서 자주 사용되며, 사후확률(posterior)과 주변확률(marginal likelihood)에 대한 닫힌 표현(closed-form expressions)를 가진다. 이것의 가장 큰 단점은 학습 데이터 수 $N$에 대해 $O(N^3)$의 계산량과 $O(N^2)$의 메모리를 쓴다는 것이다. Low-rank approximations(Quiñonero Candela & Rasmussen, 2005)는 전체 사후확률을 요약하는 $M$개의 유도변수를 사용하여 계산량을 $O(NM^2 + M^3)$, 메모리 사용량을 $O(NM + M^2)$로 줄였다.

유도변수를 추가함으로써 계산량이 줄어드는 것은 알려져 있지만, 얼마나($M$) 필요한지에 대한 정보는 별로 없다. 데이터셋이 커질수록 우리는 품질저하 없이 근사상수의 수용력이 얼마나 될지 기대할 수 없다. 단지 $N$이 커질수록 $M$이 커져야 한다는 것만 알 뿔이다.

근사 GPs는 종종 근사사후확률에서 전체사후확률과정으로의 KL divergence를 최소화하는 변분추론(variational inference)을 써서 학습된다(Titsias, 2009, Matthews et al, 2016). 이 논문에서는 근사사후확률의 품질을 위한 측정방법으로 KL divergence를 사용한다.
직관적인 가정 하에 유도변수의 수는 선형보다 느리게 증가하는 정도면 된다(예: 로그함수). 이는 많은 편향(bias)의 필요 없이 정확도와 불확실성에 대한 정확도를 보유한 근사사후확률만으로 큰 데이터셋에 대해 아주 희박한 근사만 있어도 된다는 것을 보여준다.

이 논문에서 나오는 증명의 핵심 아이디어는 데이터의 공분산행렬에 대한 Nyström 근사의 품질에 의존하는 KL divergence의 상한(상계)를 사용하는 것이다. 이 error는 무한차원의 필수연산자라는 개념으로 이해될 수 있다. Stationery kernel에 대해 메인 결과는 사전확률(priors)는 샘플함수보다 더 매끈하며(smoother) 더 집중되어 있는(more concentrated) 데이터셋은 더 희박한(sparse) 근사만으로도 충분하다는 것이다.

메인 결과

학습 입력은 고정된 독립항등분포로부터 나온 것이라는 가정 하에, 적어도 $1-\delta$의 확률로

[KL(Q \Vert \hat{P}) \le \mathcal{O} \Bigg( \frac{g(M, N)}{\sigma^2_n \delta}\Big(1 + \frac{c\Vert y \Vert^2_2}{\sigma^2_n}\Big) + N \epsilon \Bigg)]

$\hat{P}$은 posterior Gaussian process, $Q$는 변분근사, $y$는 학습 목표(training targets)이다.
함수 $g(M, N)$은 kernel과 입력의 분포에 의존하며, $N$에 따라 선형적으로 증가하며 $M$에 따라 빠르게 감소한다.
$\epsilon$은 초기품질을 결정짓는 인자로서 약간의 계산을 추가하여 임의로 작게 만들 수 있다($N$의 역승).

참고: Gaussian process regression

학습 데이터

[\mathcal{D}= { x_i, y_i }^N_{i=1}, x_i \in \chi, y_i \in \mathbb{R}]

가 관측되었을 때 Gaussian process regression을 고려해본다. 이 때 목표는 학습데이터의 제한된 수로 인해 $f(\cdot)$에 대한 불확실성을 갖고 있을 때 새로운 입력 $x^\ast$에 대해 출력값 $y^\ast$를 예측하는 것이다. $f$에 대한 사전확률을 두는 베이지안 접근법과 약간의 noise를 가진 곽츤 데이터에 대한 $f$의 우도를 고려할 때, 모델은

[f \sim \mathcal{GP}(\nu(\cdot), k(\cdot, \cdot)), \ y_i = f(x_i) + \epsilon_i, \ \epsilon_i \sim \mathcal{N}(0, \sigma^2_n)]

$\nu : \chi \rightarrow \mathbb{R}$은 평균함수이고 $k : \chi \times \chi \rightarrow \mathbb{R}$은 공분산함수이다. 로그주변우도(log marginal likelihood)는 근사의 품질과 사후확률근사가 연관되어 있다는 점에서 흥미로우며, 이는

[\mathcal{L} = -\frac{1}{2} y^T K_n^{-1} y - \frac{1}{2} log \vert K_n \vert - \frac{N}{2} log(2\pi), \quad K_n = K_{ff} + \sigma^2n I, \ [K{ff}]_{i, j} = k(x_i, x_j)]

으로 표현된다.

Training Neural Networks with Local Error Signals

최근 분류(classification)를 위한 신경망의 감독학습(supervised learning)은 보통 global loss function을 사용하여 이루어졌다. 즉, 모델을 학습시키는 데 있어서 하나의 loss function만을 설정해 두고, prediction 단계에서 계산한 loss로 backward pass 동안 gradient를 계산하며 weights를 업데이트하는 역전파(back-propagation) 과정을 거쳐왔다.

그러나 이 논문에서는 하나의 loss function을 모델의 모든 레이어에 걸쳐 global하게 사용하는 대신 각 레이어별로 loss function을 설정하여 실험하였고, 이 방법은 생물학적으로 그럴듯하고(biologically plausible) 그러면서도 여전히 state-of-the-art 결과를 얻을 수 있음을 보여주었다.

Global loss function의 사용은 다음과 같은 문제를 갖는다.

1. Backward locking problem: hidden layer의 weights들은 forward & backward pass가 끝날 때까지 업데이트되지 않는다. 따라서 weights update의 병렬화가 어렵다.
2. Preventing reuse of the memory: hidden layer의 activation들을 backward pass가 끝날 때까지 메모리에 상주시켜야 하기 때문에 메모리 사용량이 늘어난다.
3. Biologically implausible: global loss의 역전파는 신경망이라는 관점에서 생물학적으로 별로 타당하지 않다.

이 논문에서, backward locking problem은 지역적으로(각 레이어별로) 측정된 error에 의해 각각 학습시킴으로써 해결될 수 있음을 보인다. Local loss function은 global error에 의존하지 않고, gradient는 해당 레이어를 제외한 그 이전 레이어에 전파되지 않으며, hidden layer는 forward pass 중간에도 업데이트될 수 있다.
추론(inference) 단계에서 네트워크는 global 역전파를 쓰는 것과 같이 움직인다. 그러나 hidden layer가 업데이트될 때, gradient와 activation은 더 이상 메모리에 남아 있을 필요가 없다.
따라서 모든 레이어를 동시에 학습시킴에도, 지역적으로 측정된 error는 각 레이어를 학습시키며 이것을 메모리 사용량과 학습 시간을 줄여줄 수 있게 된다.

관련 연구는 Local Loss Functions, Similarity Measures in Neuroscience/Machine Learning 등이 있다(논문 참조).

표준 convolutional & fully connected 네트워크 구조를 사용하여, global loss 대신 각 레이어별로 (이전 레이어로 전파되지 않는) local learning signal을 설정했다. 이 signal은 2개의 single-layer sub-networks로 분리되어, 각각은 서로 다른 loss function을 갖는다. 하나는 표준 cross-entropy loss이고, 다른 하나는 similarity matching loss이다.

논문에서는 여러 loss를 정의하는데,

• sim loss: mini-batch의 example들 간 pair-wise 유사도를 담고 있는 두 행렬간 L2 거리를 측정하는 similarity matching loss이다.
• pred loss: target과 local classifier의 prediction 간 cosss-entropy loss를 측정한다.
• sim-bpf loss & pred-bpf loss: Backprop free version을 만들기 위해, global target이 각 hidden layer로 전파되는 것을 막는다. sim loss에서는 one-hot encoded target vector 대신 random transformation target vector를, pred loss에서는 binarized random transformation target vector를 사용한다.
• predsim & predsim-bpf loss: sim과 pred를 조합해서 전체 loss를 만들었다.

[L_{predsim} = (1-\beta)L_{pred} + \beta L_{sim}]

[L_{predsim-bpf} = (1-\beta)L_{pred-bpf} + \beta L_{sim-bpf}]

실험은 MNIST, Fashion-MNIST, Kuzushiji-MNIST, CIFAR-10, CIFAR-100, STL_10, SVHN에 대해서 각각 진행하였다.

결과를 요약하자면 단지 local pred loss만으로도 global 역전파를 사용한 것과 거의 같은 성능을 보였고, predsim이나 predsim-bpf를 사용한 경우 state-of-the-art 결과를 얻을 수 있었다고 한다.

따라서 이 논문의 contribution은 loss function을 굳이 global하게 만들지 말고 각 레이어별로 local loss function을 만들어서 backward locking problem과 parallelization을 해결하는 것이 학습속도, 생물학적 타당성, 분류 성능을 다 잡을 수 있다는 가능성을 보여준 것이 되겠다.