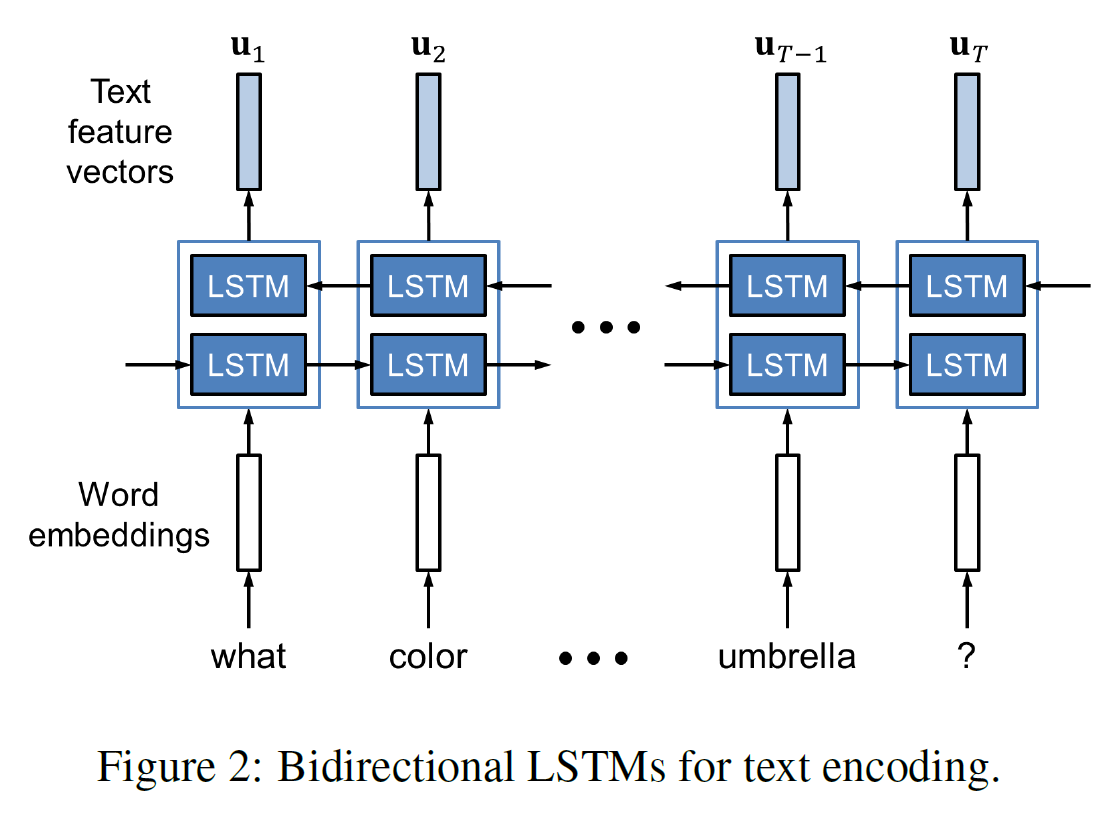
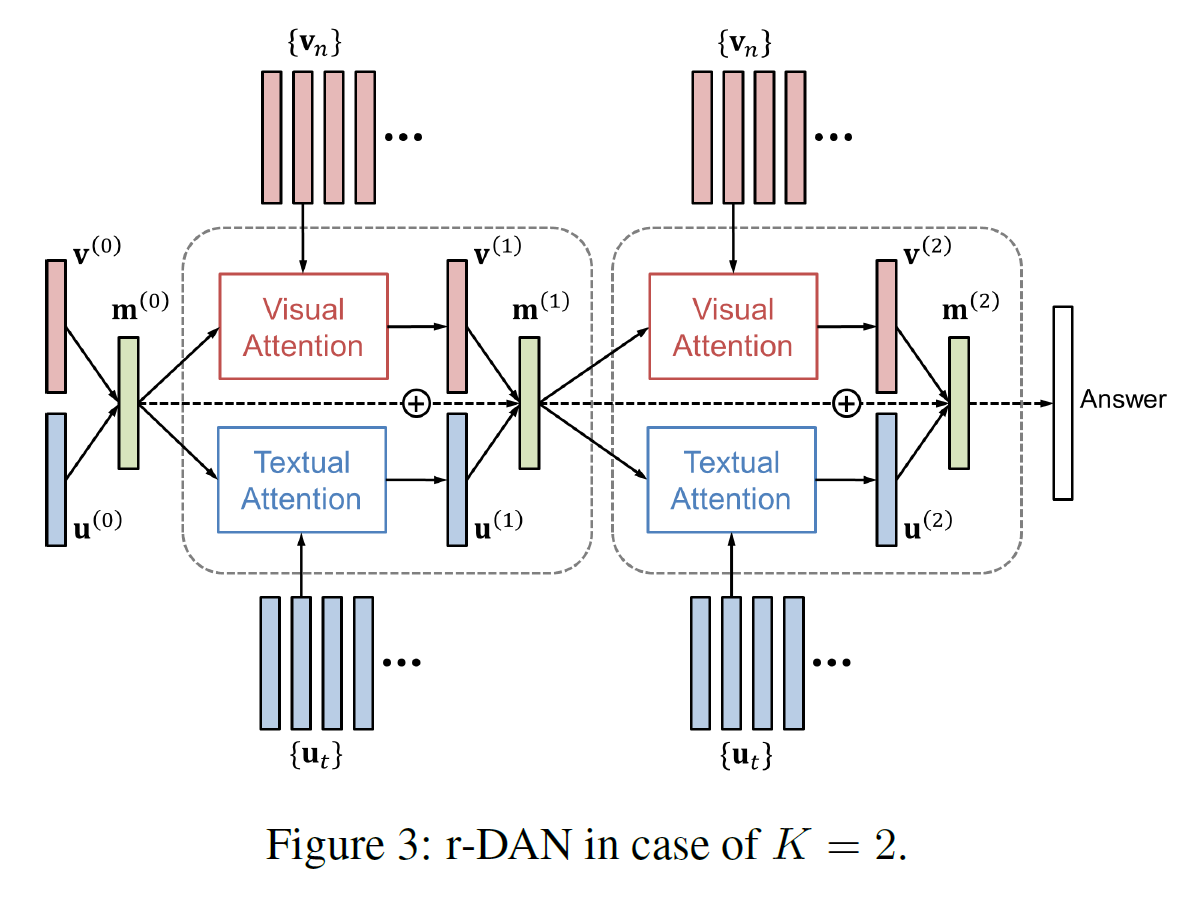
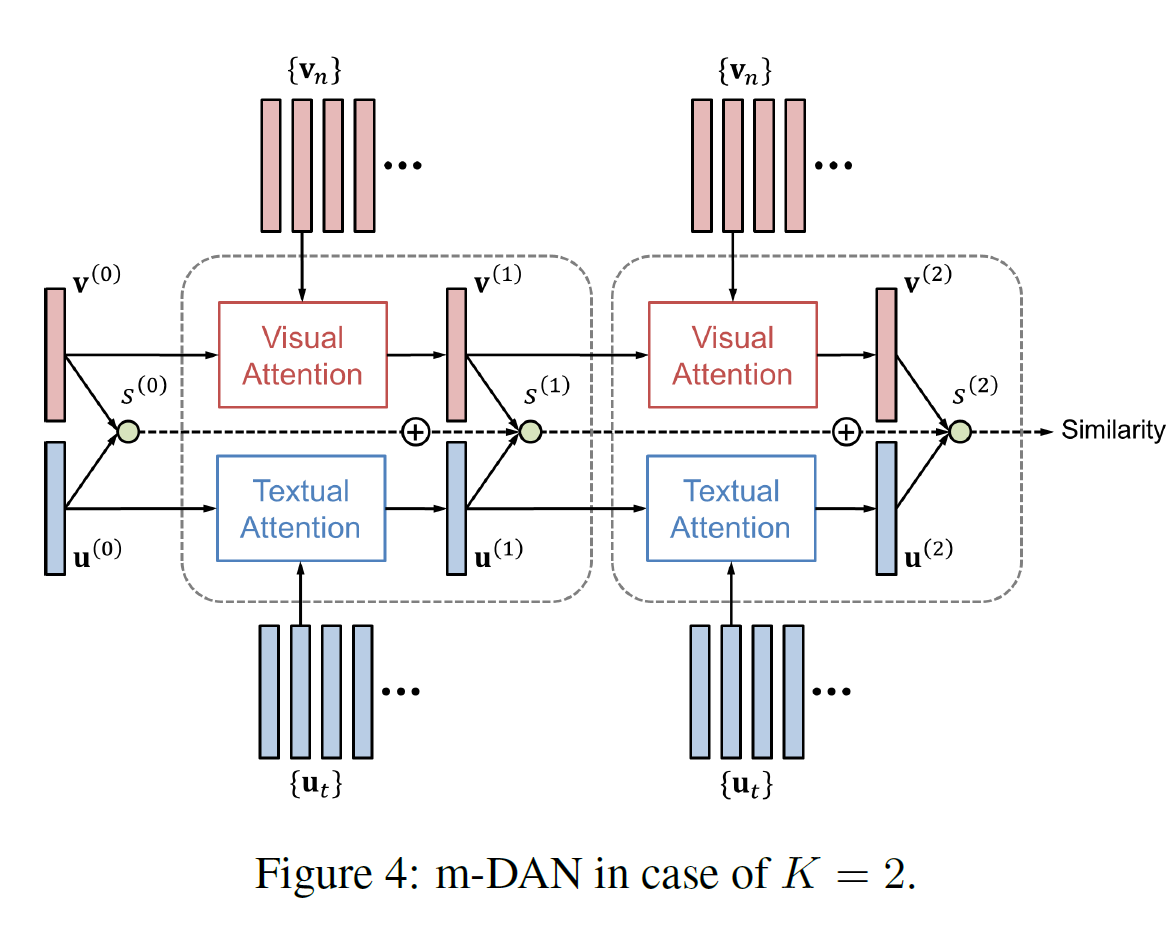
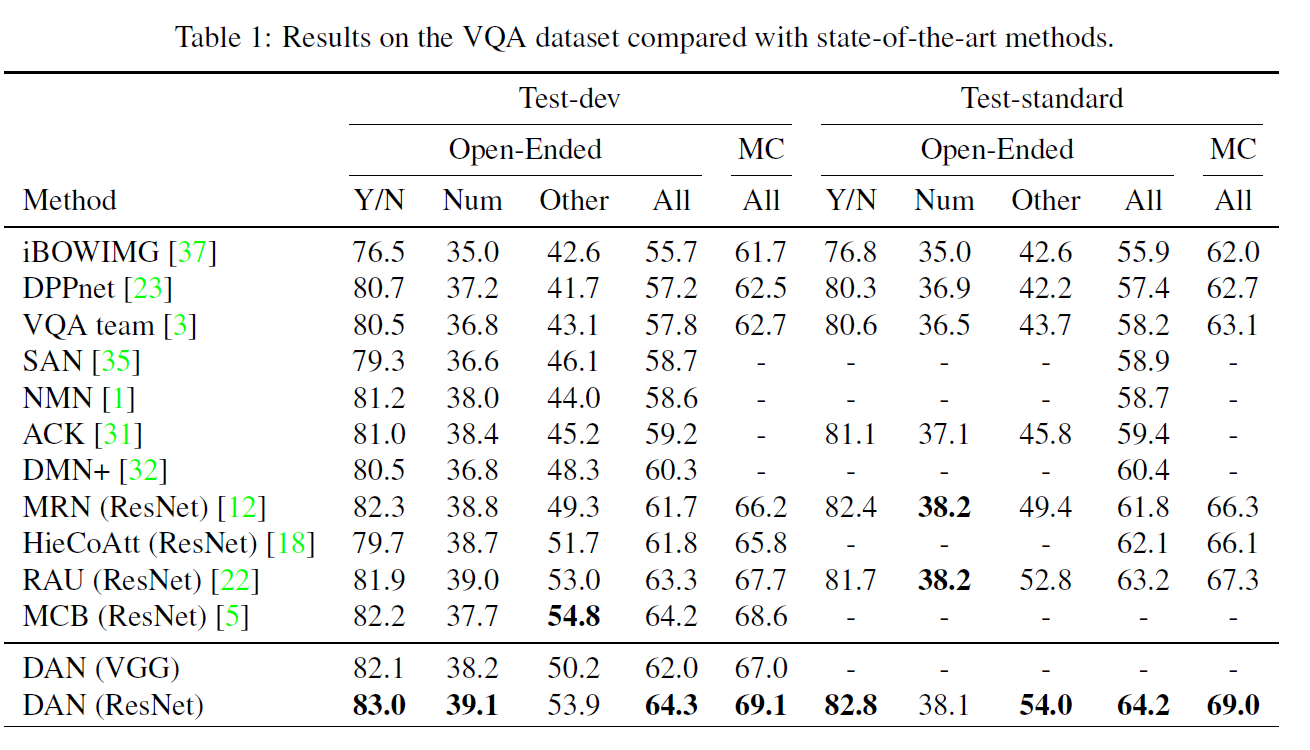
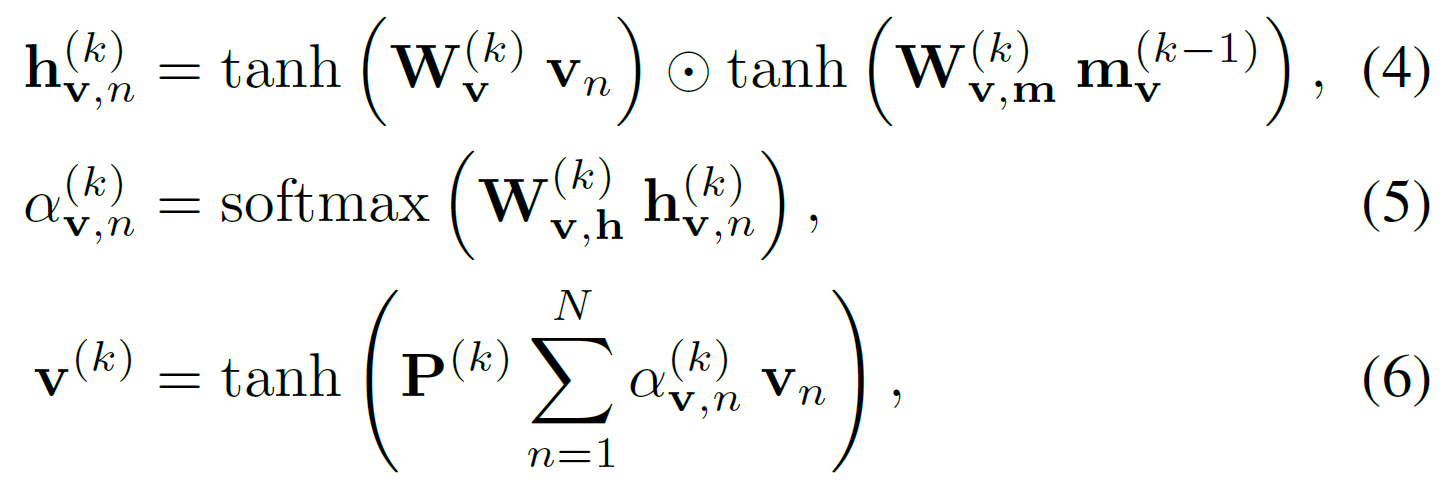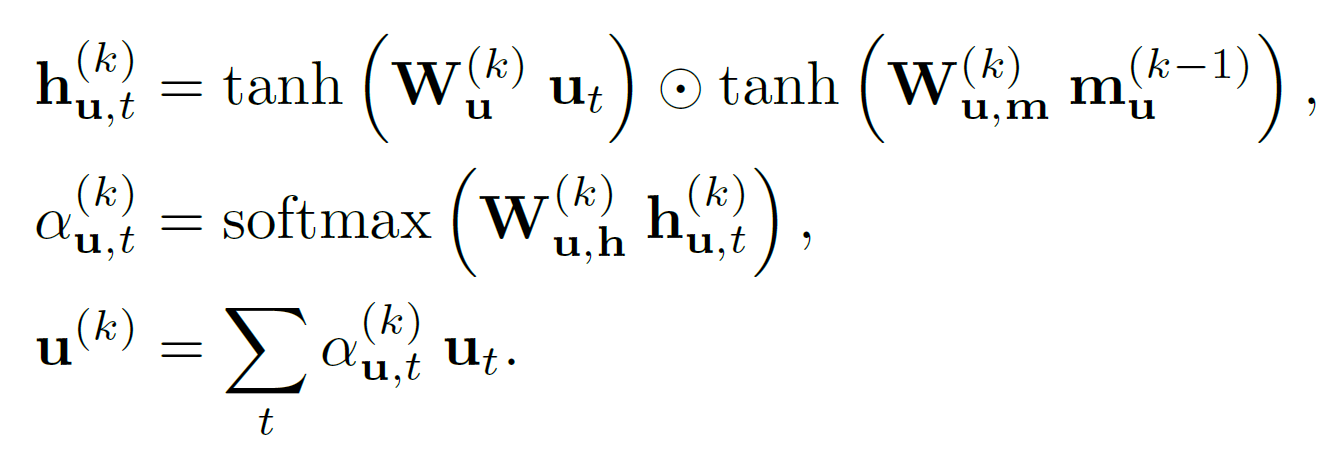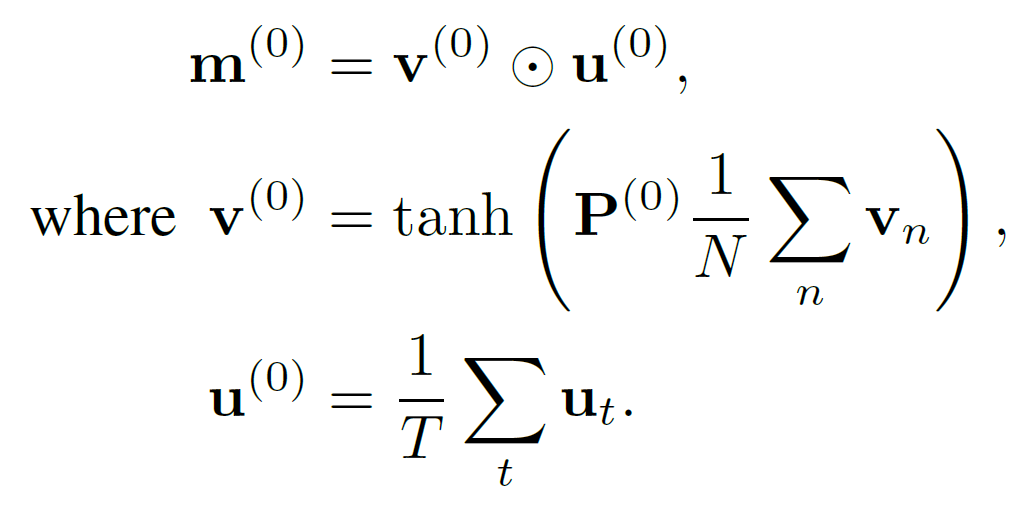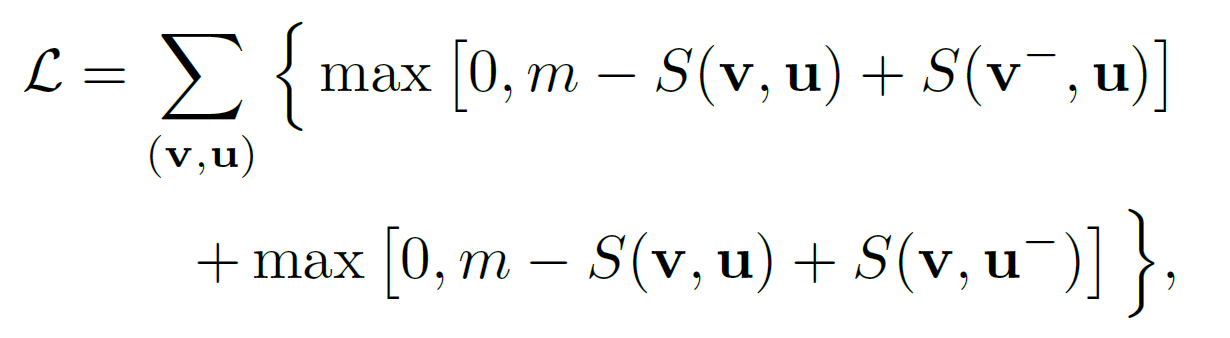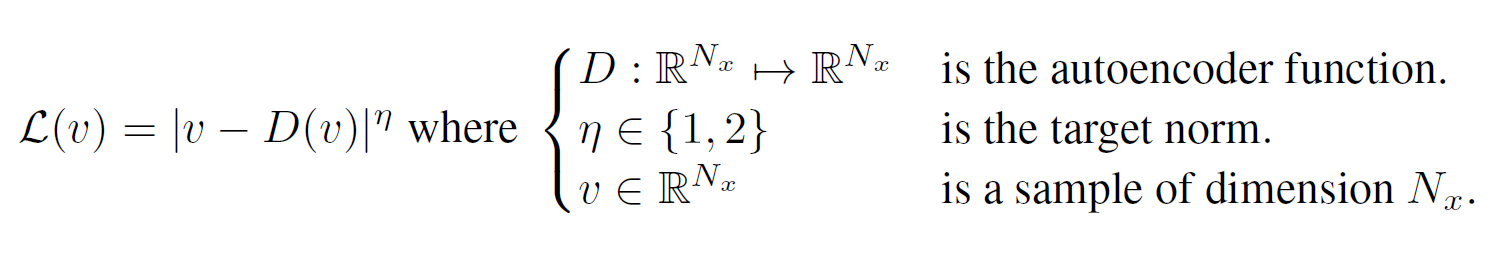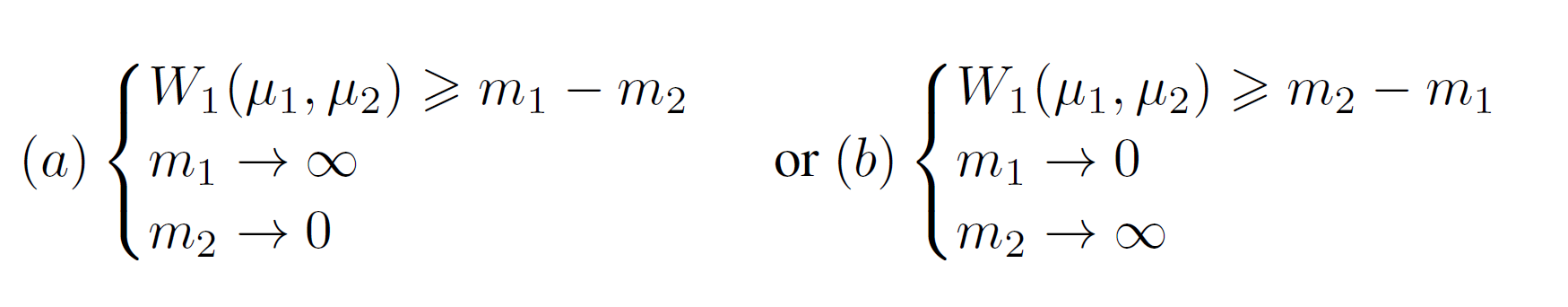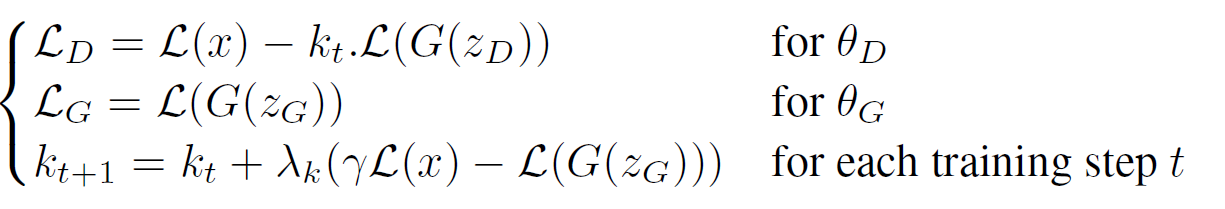이 글에서는 catGAN, Semi-supervised GAN, LSGAN, WGAN, WGAN_GP, DRAGAN, EBGAN, BEGAN, ACGAN, infoGAN 등에 대해 알아보도록 하겠다.
아래쪽의 ACGAN, infoGAN은 발표 시기가 아주 최신은 아니지만 conditional GAN(CGAN)의 연장선상에 있다고 할 수 있기 때문에 따로 빼 놓았다.
각각에 대해 간단히 설명하면,
- catGAN(Categorical GAN): D가 real/fake만 판별하는 대신 class label/fake class을 출력하도록 바꿔서 unsupervised 또는 semi-supervised learning이 가능하도록 하였고 또한 더 높은 품질의 sample을 생성할 수 있게 되었다.
- Semi-supervised GAN: catGAN과 거의 비슷하다. original GAN과는 달리 DCGAN을 기반으로 만들어졌다.
- LSGAN: 진짜 분포 $ p_{data} $와 가짜 데이터 분포 $p_g$를 비슷하게 만들기 위해, decision boundary에서 멀리 떨어진 sample에게 penalty를 주어 진짜 데이터에 근접하게 만드는 아이디어를 사용했다. 이름답게 loss function에는 Least Square가 사용되었고, 이를 통해 더 선명한 출력 이미지와 학습 과정의 높은 안정성을 얻었다. 또한, 이 최적화 과정이 $\chi^2$ divergence 최소화와 같음을 보였다.
- WGAN: 실제 데이터의 분포와 가짜 데이터의 분포의 거리를 측정하는 방법으로 Wasserstein Distance를 정의하여 가짜 데이터를 실제 데이터에 근접하도록 하는 방법을 제시하였는데, 기존의 GAN들이 최적 값으로 잘 수렴하지 않던 문제를 해결, 거의 대부분의 데이터셋에서 학습이 잘 되는 GAN을 만들어냈다.
- WGAN_GP: Improved WGAN이다. WGAN이 k-Lipschitz constraints를 만족시키기 위해 단순히 clipping을 수행하는데, 이것이 학습을 방해하는 요인으로 작용할 수 있다. WGAN_GP에서는 gradient penalty라는 것을 목적함수에 추가하여 이를 해결하였고, 학습 안정성을 데이터셋뿐만 아니라 모델 architecture에 대해서도 얻어냈다.
- DRAGAN: Deep Regret Analytic GAN이다. WGAN에 더불어 gradient penalty를 정규화하고 더 다듬어 gradient penalty schemes(또는 heuristics)를 만들었고, 이를 저자들은 DRAGAN algorithm이라 하였다. 결과적으로 여전히 남아 있던 mode collapse 문제를 더 완화하였다.
- EBGAN: Energy-Based GAN. 지금까지 대부분의 GAN이 D가 real일 확률을 0/1로 나타냈었다면, 이 모델은 그 구조를 깨고 에너지 기반 모델로 바꿨다는 데 의의가 있다. 그래서 D는 단지 real/fake를 구분하는 것이 아닌 G에 대한 일종의 loss function처럼 동작하며, 실제 구현은 Auto-Encoder으로 이루어졌다.
- BEGAN: Boundary Equilibrium GAN으로, EBGAN을 베이스로 하고 Watterstein distance를 사용하였으며, 모델 구조를 단순화하고 이미지 다양성과 품질 간 trade-off를 조절할 수 있는 방법 또한 알아냈다고 한다. 이 논문에서는 스스로 milestone한 품질을 얻었다고 한다.
- ACGAN: D를 2개의 분류기로 구성하고 목적함수도 두 개로 나눠서 real/fake, 데이터의 class를 구하는 과정을 분리하여 disentangled한 $z$를 만들었다.
- infoGAN: 많은 GAN들이 그 내부의 parameter가 심하게 꼬여(entangled) 있고 이는 parameter의 어떤 부분이 어느 역할을 하는지 전혀 알 수 없게 만든다. infoGAN에서는 이를 잘 분리하여, semantic feature를 잘 조작하면 어떤 인자를 조작했느냐에 따라 생성되는 이미지의 각도, 밝기, 너비 등을 임의로 조작할 수 있게 하였다.
이 글에 소개된 대부분의 GAN은 다음 repository에 구현되어 있다.
Pytorch version
Tensorflow version
catGAN
논문 링크: catGAN
2015년 11월 처음 제안되었다.
데이터의 전체 또는 일부가 unlabeled인 경우 clustering은 $p_x$를 직접 예측하는 generative model과 분포를 예측하는 대신 데이터를 직접 잘 구분된 카테고리로 묶는 discriminative model로 나누어지는데, 이 모델에서는 이 두 아이디어를 합치고자 했다.
논문에서 이 catGAN은 original GAN이 $real, fake$만 구분하던 것을 real인 경우에는 그 class가 무엇인지까지 구분하게($C_1, C_2, …, C_N, C_{fake}$)했다는 점에서 original GAN의 일반화 버전이라고 하였으며, 또한 RIM(Regularized Information Maximization)에서 regularization이 추가가 되었듯 catGAN에선 G가 D에 대한 regularization을 하기 때문에 RIM의 확장판이라고도 하였다.
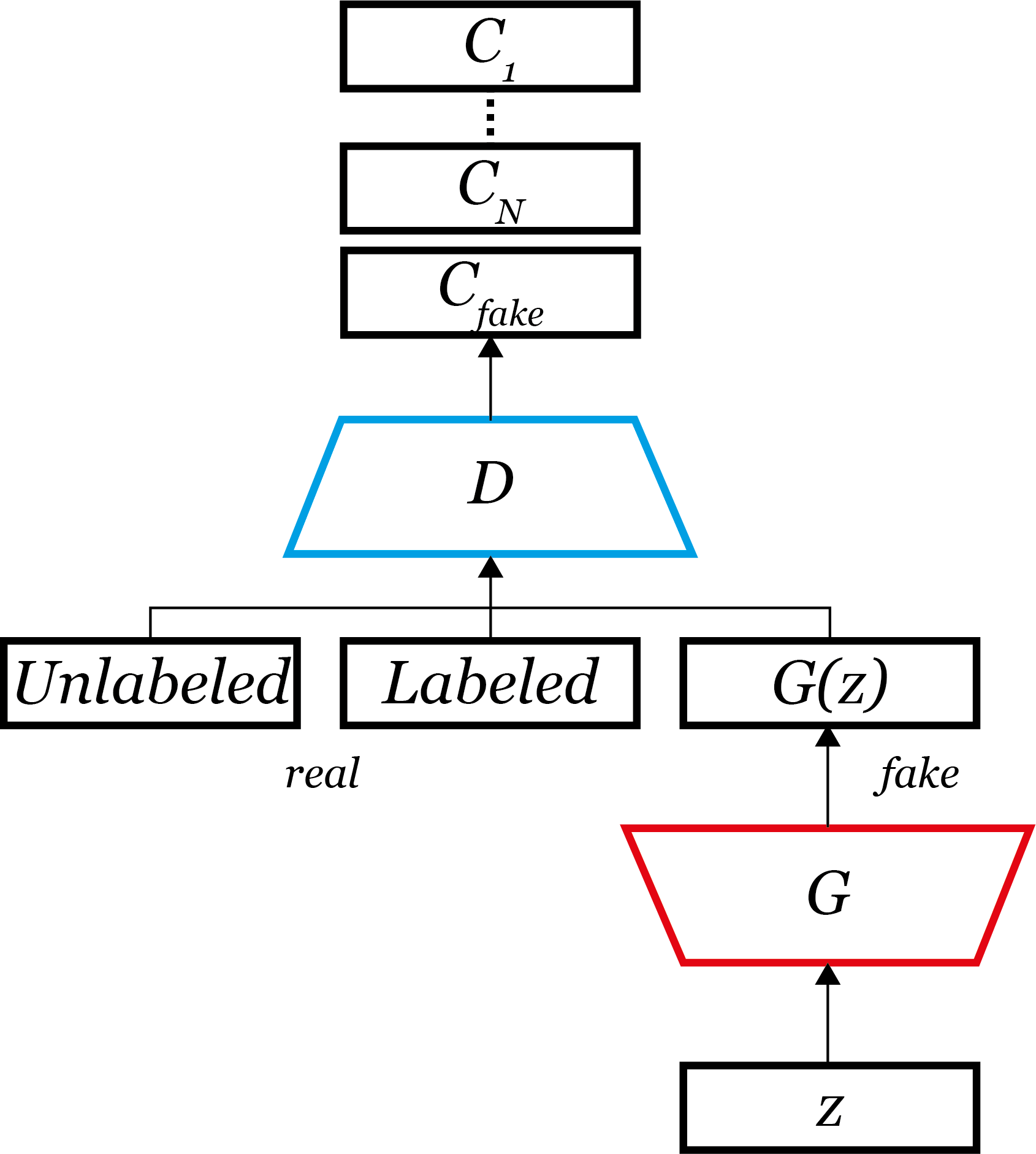
RIM에서 최적의 unsupervised classifier의 목적함수로 엔트로피를 사용하였듯 catGAN도 목적함수로 엔트로피 개념을 사용한다. 아래는 논문에 나온 그림이다.
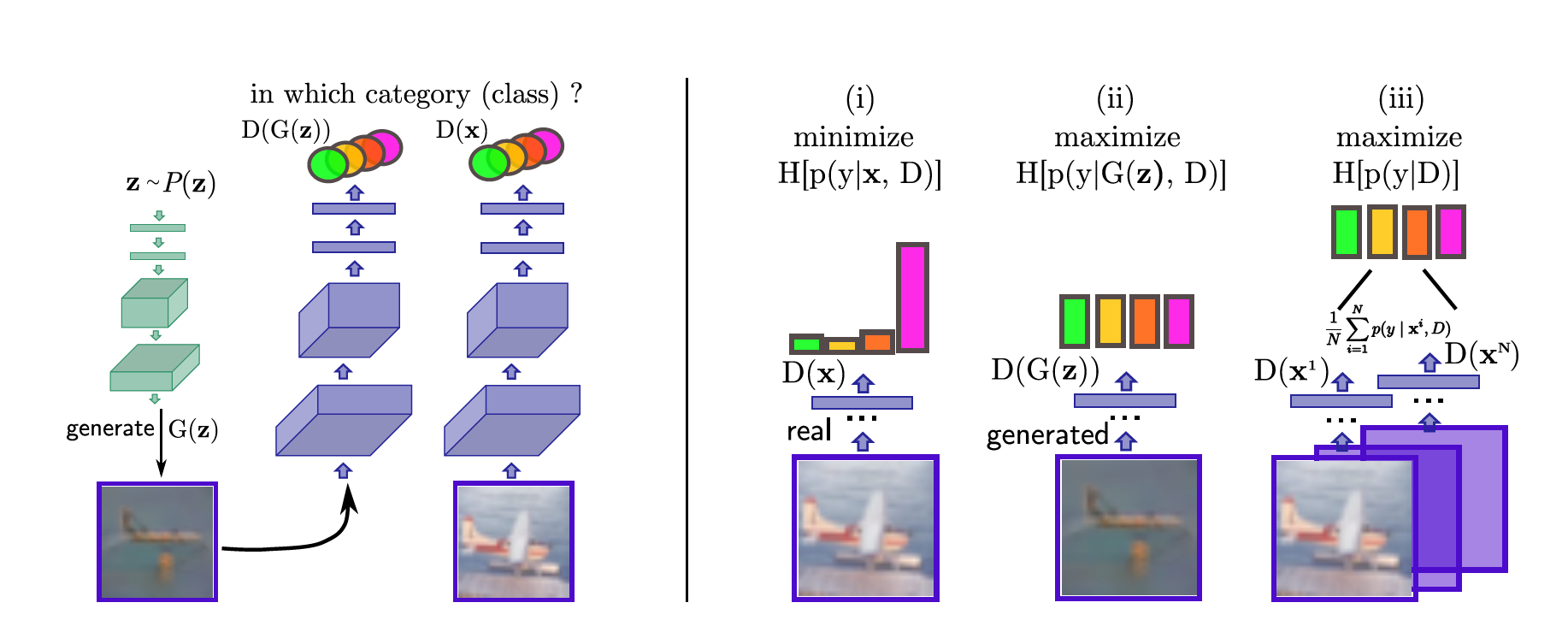
왼쪽에서 초록색은 G(generate라고 되어 있다), 보라색은 D를 의미한다. 여기서 H는 엔트로피이다.
오른쪽 그림을 보면, D의 입장에서는:
- i) real data는 실제 class label을 딱 하나 갖고 있기 때문에 해당하는 label일 확률만 1에 가깝고 나머지는 0이어야 한다. 따라서 엔트로피( $ H[p(y \vert x, D)] $ )를 최소화한다.
- ii) fake data의 경우 특정 class에 속하지 않기 때문에 class label별로 확률은 비슷해야 한다. 따라서 엔트로피$H[p(y \vert x, G(z))]$를 최대화한다.
- iii) 학습 sample이 특정 class에 속할 확률이 비슷해야 한다는 가정을 했기 때문에, input data $x$에 대한 marginal distribution(주변확률분포)의 엔트로피($H[p(y \vert D)]$)가 최대가 되어야 한다.
G의 입장에서는:
- D를 속여야 하기 때문에 G가 만든 가짜 데이터는 가짜임에도 특정 class에 속한 것처럼 해야 한다. 즉, D의 i) 경우처럼 엔트로피($H[p(y \vert x, G(z))]$)를 최소화한다.
- 생성된 sample은 특정 class에 속할 확률이 비슷해야 하기 때문에 marginal distribution의 엔트로피($H[p(y \vert D)]$)가 최대화되어야 한다.
따라서 D와 G의 목적함수를 정리하면,
| [L_D = max_D ~~~ H_{\chi}[p(y |
D)] - \mathbb{E}_{x\sim \chi} [H[p(y |
x, D)]] + \mathbb{E}_{z\sim P(z)}[H[p(y |
G(z), D)]]] |
| [L_G = min_G ~~~ H_G[p(y |
D)] + \mathbb{E}_{z\sim P(z)}[H[p(y |
G(z), D)]]] |
다만 $L_D$의 마지막 항을 직접 구하는 것은 어렵기 때문에, $z \sim P(z) $를 $M$개 뽑아 평균을 계산하는 몬테카를로 방법을 쓴다.
위 목적함수를 사용하여 실험한 결과는 다음과 같다.
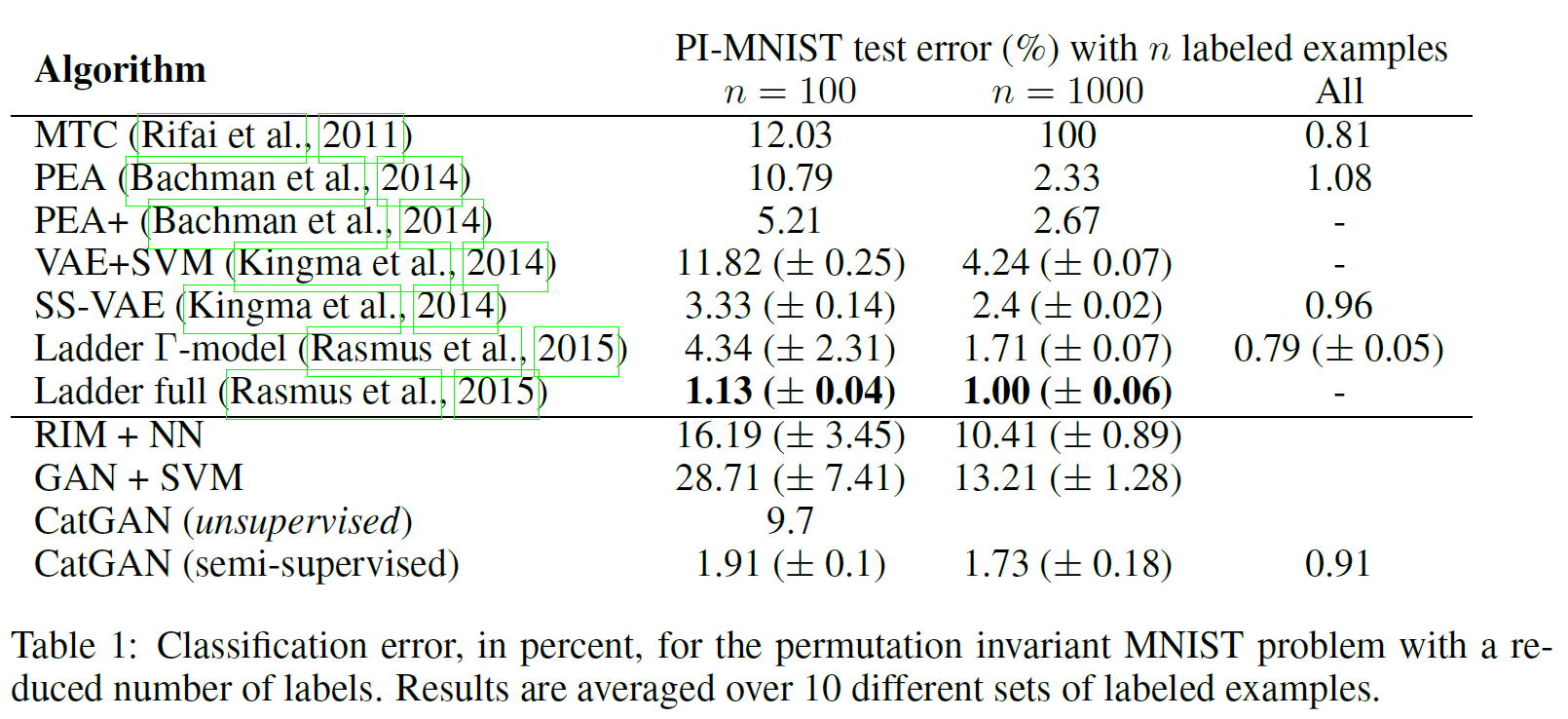
Unsupervised catGAN은 9.7%의 error를 보이는 데 반해 $n=100$만의 labeled data가 있는 버전의 경우 error가 1.91%까지 떨어진다. $n=1000$, $n=전체$인 경우 error는 점점 떨어지는 것을 볼 수 있다. 즉, 아주 적은 labeled data를 가진 semi-supervised learning이라도 굉장히 쓸모있다는 뜻이다.
또한 k-means나 RIM과 비교했을 때 두 원을 잘 분리해내는 것을 볼 수 있다.

MNIST나 CIFAR-10 데이터도 잘 생성해내는 것을 확인하였다.

Semi-supervised GAN
논문 링크: Semi-supervised GAN
2016년 6월 처음 제안되었다.
위의 catGAN과 거의 비슷한 역할을 한다. 전체적인 구조도 비슷하다.
논문 자체가 짧고 목적함수에 대한 내용이 없어서 자세한 설명은 생략한다. 특징을 몇 개만 적자면,
- original GAN과는 달리 sigmoid 대신 softmax를 사용하였다. $N+1$개로 분류해야 하니 당연하다.
- DCGAN을 기반으로 작성하였다.
- D가 classifier의 역할을 한다. 그래서 논문에서는 D/C network라고 부른다(D이자 C).
- classifier의 정확도는 sample의 수가 적을 때 CNN보다 더 높다는 것을 보여주었다. sample이 많을 때는 거의 같았다.
- original GAN보다 생성하는 이미지의 품질이 좋다.

LSGAN
논문 링크: LSGAN
2016년 11월 처음 제안되었다.
original GAN의 sigmoid cross entropy loss function은 vanishing gradients 문제가 있고, 따라서 출력 이미지는 실제 이미지에 비해선 분명히 품질이 떨어진다.
아래 그림의 (b)에서, 오른쪽 아래의 가짜 데이터는 D를 잘 속이고 있지만 vanishing gradient(sigmoid 그래프의 양쪽 끝을 생각하라) 문제로 인해 거의 업데이트되지 않고, 따라서 가짜 이미지는 실제 이미지와는 동떨어진 결과를 갖는다.
그러나 (c)처럼 이렇게 경계로부터 멀리 떨어진 sample들을 거리에 penalty를 줘서 경계 근처로 끌어올 수 있다면 가짜 이미지는 실제에 거의 근접하게 될 것이다. LSGAN은 이 아이디어에서 출발한다.
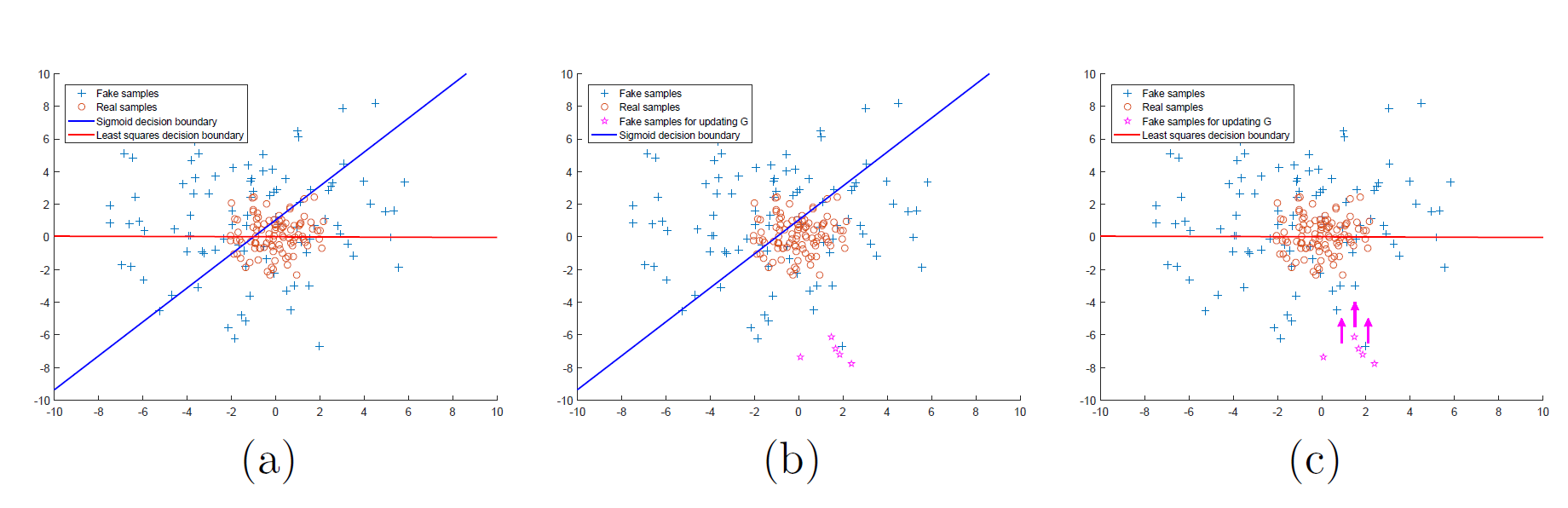
그래서, D를 위한 loss function을 least squares로 대체하면, 경계(decision boundary)로부터 먼 sample들은 penalty를 받아 경계 근처로 끌려온다.
original GAN의 목적함수는 다음과 같았다.
[min_G max_D V(D, G) = \mathbb{E}{x \sim p{data}(x)}[log D(x)] + \mathbb{E}{x \sim p{z}(z)}[log (1-D(G(z)))]]
LSGAN의 목적함수는 다음과 같다. $a$: fake data label , $b$: real data label.
$c$: G가 원하는 것은 이 $c$라는 값을 D가 fake data라고 믿는 것이다.
[min_D V_{\text{LSGAN}}(D) = \frac{1}{2} \mathbb{E}{x \sim p{data}(x)}[(D(x)-b)^2] + \frac{1}{2} \mathbb{E}{x \sim p{z}(z)}[(D(G(z)) - a)^2]]
[min_G V_{\text{LSGAN}}(G) = \frac{1}{2} \mathbb{E}{x \sim p{z}(z)}[(D(G(z)) - c)^2]]
이렇게 목적함수를 바꿈으로써 얻는 이득은 두 가지다.
- original GAN과는 달리 decision boundary에서 멀리 떨어진 sample을 오랫동안 가만히 두지 않고, 설령 맞는 영역에 위치한다고 해도 이에 penalty를 준다. 이는 결과적으로 G가 이미지를 생성할 때 decision boundary에 최대한 가까운, 즉 실제 이미지에 가깝게 생성하도록 한다.
- 멀리 떨어진 sample일수록 square 함수에 의해 penalty를 크게 받는다. 따라서 vanishing gradients 문제가 많이 해소되며, 따라서 학습이 안정적이게 된다. original GAN의 sigmoid는 $\vert x \vert$가 클 때 gradient가 매우 작다.
또 한 가지 더: LSGAN의 목적함수를 최적화하는 과정은 $\chi^2$ divergence를 최소화하는 것과 같다.
간략히 설명하면,
original GAN에서는 최적화 과정이 Jensen-Shannon divergence를 최소화하는 것을 보였다.
[C(G) = KL \biggl( p_{data} \Vert \frac{p_{data}+p_g}{2} \biggr) + KL \biggl( p_{g} \Vert \frac{p_{data}+p_g}{2} \biggr) - log(4)]
이제 LSGAN의 목적함수를 확장해 보면,
[min_D V_{\text{LSGAN}}(D) = \frac{1}{2} \mathbb{E}{x \sim p{data}(x)}[(D(x)-b)^2] + \frac{1}{2} \mathbb{E}{x \sim p{z}(z)}[(D(G(z)) - a)^2]]
[min_G V_{\text{LSGAN}}(G) = \frac{1}{2} \mathbb{E}{x \sim p{data}(x)}[(D(x)-c)^2] + \frac{1}{2} \mathbb{E}{x \sim p{z}(z)}[(D(G(z)) - c)^2]]
$ V_{\text{LSGAN}}(G) $의 추가된 항은 G의 parameter를 포함하지 않기 때문에 최적값에 영향을 주지 않는다.
우선 G를 고정했을 때 D의 최적값은:
[D^\ast(x) = {bp_{data}(x) + ap_g(x) \over p_{data}(x) + p_g(x)}]
중간 과정을 조금 생략하고 적으면, $b-c=1, b-a=2$라 했을 때
[2C(G) = \mathbb{E}{x \sim p{data}} [(D^\ast(x)-c)^2] + \mathbb{E}{x \sim p{g}} [(D^\ast(x)-c)^2]]
[= \int_\chi {((b-c)(p_d(x) + p_g(x)) - (b-a)p_g(x))^2 \over p_d(x) + p_g(x)} dx]
[= \int_\chi {(2p_g(x) - (p_d(x) + p_g(x)))^2 \over p_d(x) + p_g(x)} dx]
[= \chi^2_{Pearson} (p_d + p_g \Vert 2p_g)]
그러므로 LSGAN의 최적화 과정은 $b-c=1, b-a=2$일 때 $p_d + p_g$와 $2p_g$ 사이의 Pearson $\chi^2$ divergence를 최소화하는 과정과 같다.
학습시킬 때 $a, b, c$ 값을 $a=-1, b=1, c=0$ 또는 $a=0, b=c=1$ 등을 쓸 수 있다. 둘 사이의 차이는 실험 결과 별로 없으므로, 논문에서는 후자를 택했다.
LSGAN의 구조는 두 가지가 제안되어 있다. 하나는 112$ \times $112 size의 이미지를 출력하는 모델, 다른 하나는 class 개수가 3470개인 task를 위한 것(한자를 분류한다)인데, 충분히 읽기 쉬운 글자를 만들어내는 것을 볼 수 있다.
아래에 모델 구조를 나타내었다.
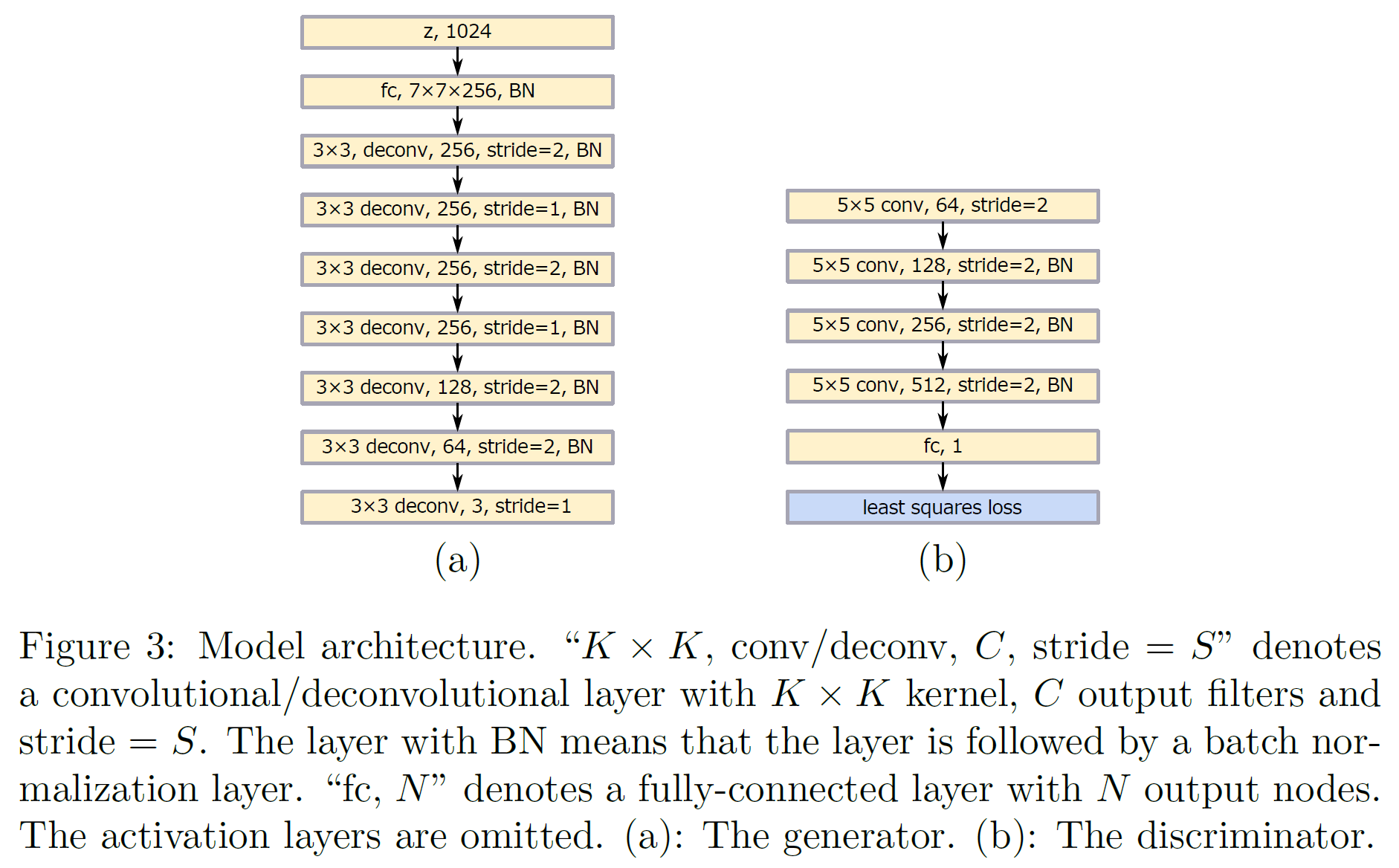
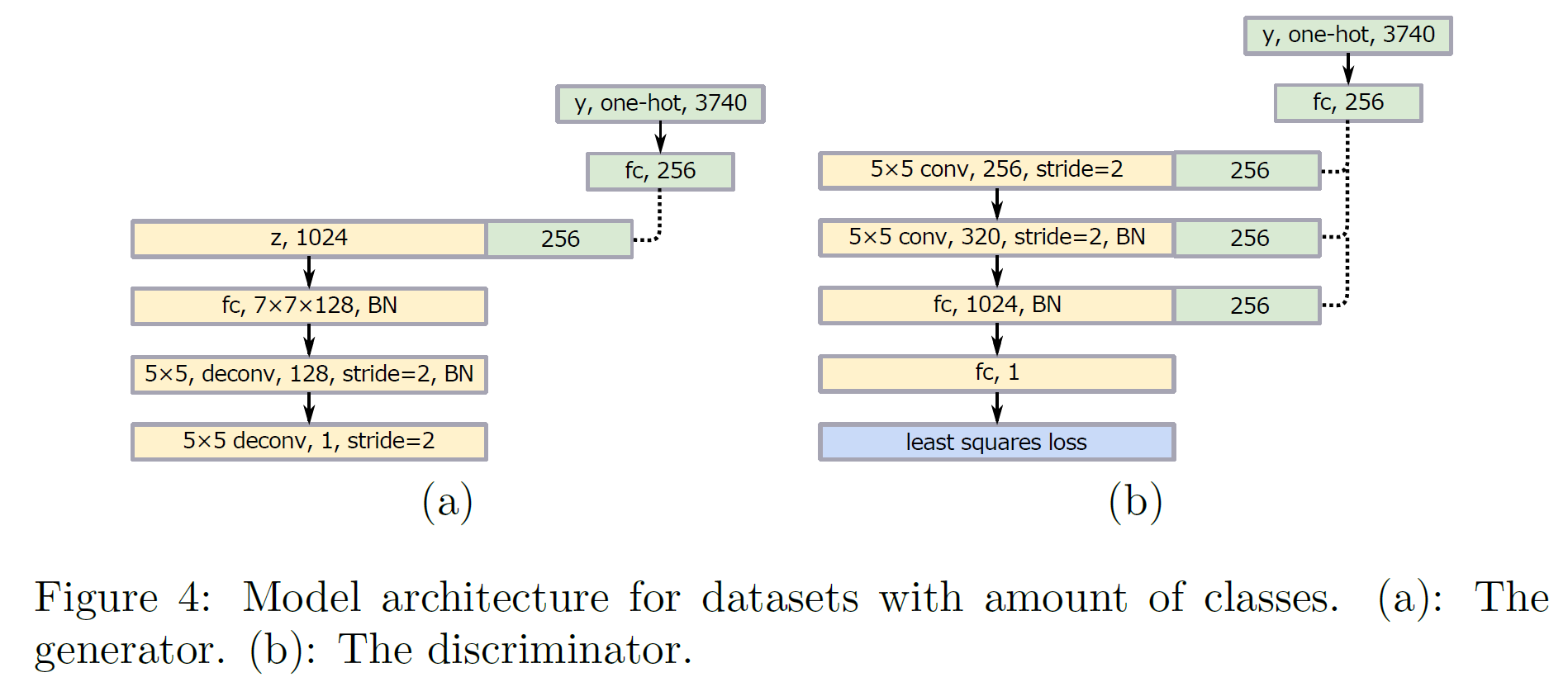
많은 class 수를 가진 경우 생성된 이미지 품질이 좋지 못한데, 이유는 입력 class 종류는 매우 많지만 출력은 하나뿐이기 때문이다. 이를 해결하는 방법은 conditional GAN을 쓰는 것이다.
그러나 one-hot encoding은 너무 비용이 크기 때문에 그 대신 각각의 class에 대응하는 작은 벡터를 linear mapping을 통해 하나 만들어서 모델의 레이어에 붙이는 방식을 썼다. 그 결과가 위 그림과 같으며, 목적함수는 다음과 같이 정의된다:
[min_D V_{\text{LSGAN}}(D) = \frac{1}{2} \mathbb{E}{x \sim p{data}(x)}[(D(x \vert \Phi(y))-1)^2] + \frac{1}{2} \mathbb{E}{x \sim p{z}(z)}[(D(G(z) \vert \Phi(y)))^2]]
[min_G V_{\text{LSGAN}}(G) = \frac{1}{2} \mathbb{E}{x \sim p{z}(z)}[(D(G(z \vert \Phi(y))) - 1)^2]]
$y$는 label vector, $ \Phi(\cdot) $은 linear mapping 함수이다.
LSUN-bedroom 등 여러 데이터셋에 대한 실험 결과이다.




마지막 그림의 경우 한자 글자를 꽤 잘 생성해내는 것을 볼 수 있다.
LSGAN도 GAN의 역사에서 꽤 중요한 논문 중 하나이다.
WGAN
논문 링크: WGAN
2017년 1월 처음 제안되었다.
소스코드: pytorch
참고할 만한 사이트: 링크
이 논문도 f-GAN처럼 수학으로 넘쳐흐른다. 다만 요약하지 않을 뿐
이 논문의 수학을 이해하는 데 있어 매우 좋은 참고자료가 있다: 링크
이 논문은 실제 데이터 분포와 가짜 데이터 분포 사이의 거리를 측정하는 방법을 바꿈으로써 GAN이 매우 안정적인 학습을 할 수 있도록 만들었다는 것에 의의가 있다.
기억할 것은 하나다: 거의 대부분의 데이터셋에서 학습이 안정적으로 잘 진행된다(다만 경우에 따라 약간 느리다고 한다).
original GAN부터 시작해서 GAN의 기본 아이디어는 두 분포 사이의 거리를 최소화하도록 G(와 D)를 잘 학습시키는 것이다. original GAN의 경우 이 최적화 과정이 Jenson-Shannon divergence(JSD)를 최소화하는 것과 같다는 것은 이미 증명되어있다.
그러나 이 JSD는 모든 분포의 거리를 효과적으로 측정해주지 못한다. 예를 들어
[\mathbb{P}0(x=0, y>0), \quad \mathbb{P}\theta(x=\theta, y>0)]
두 (반직선 형태인) 분포 간의 거리를 JSD로 측정하면,
[JS ( \mathbb{P}{0}, \mathbb{P}\theta ) = 0 \ \ if \ \theta=0, \quad log \ 2 \quad otherwise]
즉, $ \theta $가 1이든 0.0001이든 상관없이 두 분포가 얼마나 가까운지에 대한 정보를 JSD는 전혀 제공해주지 못한다. 이는 KL divergence도 마찬가지이다.
[KL ( \mathbb{P}{0}, \mathbb{P}{\theta}) = 0 \ \ if \ \theta=0, \quad \infty \quad otherwise]
참고로 논문에 나온 다른 측정방식으로 Total Variation(TV)이 있는데 별반 다를 것은 없다.
[\lambda( \mathbb{P}{0}, \mathbb{P}{\theta}) = 0 \ \ if \ \theta=0, \quad 1 \quad otherwise]
참고로 TV는 이렇게 정의된다.
[\delta(\mathbb{P}r, \mathbb{P}_g) = sup{A \in \Sigma} \vert \mathbb{P}_r(A) - \mathbb{P}_g(A) \vert]
그래서 WGAN의 저자들은 이와 비슷한 분포를 가진 경우 등은 GAN이 수렴을 잘 하지 못할 것이라고 하며 분포 간 거리를 측정하는 새로운 Earth-Mover(EM) distance 또는 Wasserstein-1 distance라고 부르는 것을 제안했다.
[W(\mathbb{P}r, \mathbb{P}_g) = \text{inf}{\gamma \in \Pi(\mathbb{P}r, \mathbb{P}_g)} \int d(x, y) \gamma (dxdy) \ \qquad = \text{inf}{\gamma \in \Pi(\mathbb{P}r, \mathbb{P}_g)} \ \mathbb{E}{(x, y) \sim \gamma} [ \Vert x - y \Vert ]]
$\Pi(\mathbb{P}, \mathbb{Q})$는 두 확률분포 $\mathbb{P}, \mathbb{Q}$의 결합확률분포들의 집합이고, $\gamma$는 그 중 하나이다.
즉 위 식은 모든 결합확률분포 $\Pi(\mathbb{P}, \mathbb{Q})$ 중 $d(x,y)$의 기댓값을 가장 작게 추정한 값이다.
이제 이 식을 위 그림의 두 분포에 적용하면 거리는
[W(\mathbb{P}0, \mathbb{P}\theta) = \vert \theta \vert]
로 아주 적절하게 나온다.
그래서 이렇게 나온 Wasserstein distance는 $\mathbb{P}_r$과 $\mathbb{P}_\theta$ 사이의 거리를 $\mathbb{P}_r$를 $\mathbb{P}_\theta$로 옮길 때 필요한 양과 거리의 곱으로 측정한다.
이를 어떤 산(분포) 전체를 옮기는 것과 같다고 해서 Earth Mover 또는 EM distance라고 불린다.
[Cost = mass \times distance]
original GAN과 목적함수의 차이를 비교하면,
| name |
Discriminator |
Generator |
| GAN |
$\nabla_{\theta_d} \frac{1}{m} \sum^m_{i=1} \ [log D(x^{(i)}) + log (1-D(G(z^{(i)})))] $ |
$\nabla_{\theta_g} \ \frac{1}{m} \sum^m_{i=1} log (D(G(z^{(i)}))) $ |
| WGAN |
$\nabla_w \frac{1}{m} \ \sum^m_{i=1} \ [f(x^{(i)}) + f(G(z^{(i)}))] $ |
$\nabla_{\theta} \frac{1}{m} \ \sum^m_{i=1} \ f(G(z^{(i)})) $ |
차이점이 더 있는데,
- $f$는 k-Lipschitz function이어야 한다. 이를 위해 WGAN에서는 단순히 $[c, -c]$로 clipping한다.
- log_sigmoid를 사용하지 않는다.
이제 WGAN 논문에 제시된 알고리즘을 보자.

알고리즘에 굉장히 특별하진 않다. optimizer로 RMSProp을 사용한 것이 약간의 차이점이다.
학습 과정에서의 장점을 보여주는 그림이 논문에 제시되어 있다. 두 Gaussian 분포를 볼 때 GAN의 수렴이 훨씬 잘 된다는 말이다.
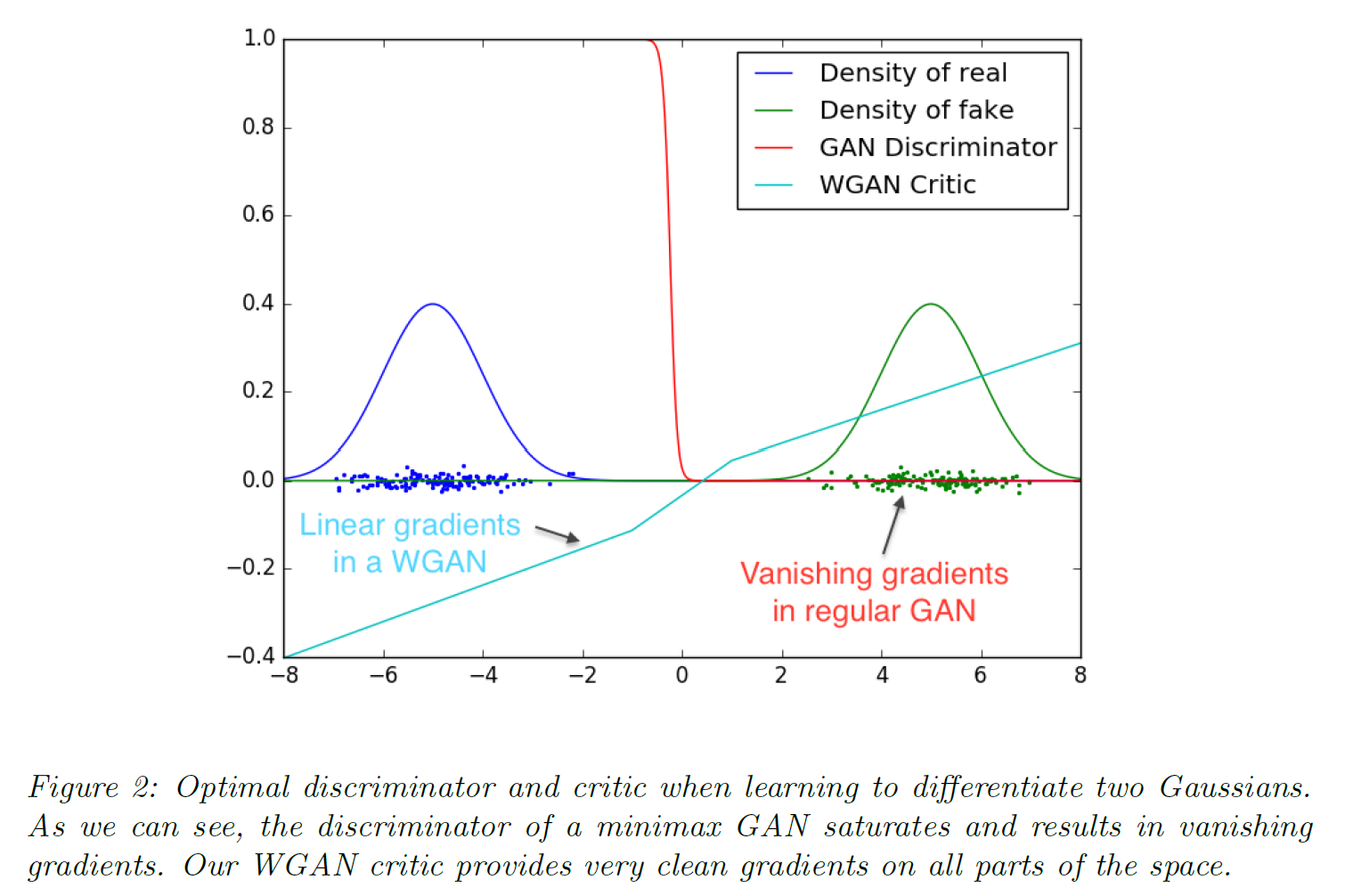
WGAN 실험 결과를 보면 다음과 같다.

\(\\\)
사실 이 논문은 부록을 포함해 32page짜리 논문으로 수학이 넘쳐흐르지만, 필자의 논문 리뷰는 이 논문이 무슨 내용인지 정도만 전달하려는, 내용을 적당히 요약하여 보여주는 것이 목적이므로 자세한 수식 및 증명 과정은 따로 적지 않는다.
궁금하면 직접 읽으면 된다
Improved WGAN
논문 링크: WGAN_GP
2017년 3월 처음 제안되었다.
소스코드: pytorch
참고할 만한 사이트: 링크
WGAN은 clipping을 통해 Lipschitz 함수 제약을 해결하긴 했지만, 이는 예상치 못한 결과를 초래할 수 있다:
(WGAN 논문에서 인용)
만약 clipping parameter($c$)가 너무 크다면, 어떤 weights든 그 한계에 다다르기까지 오랜 시간이 걸릴 것이며, 따라서 D가 최적화되기까지 오랜 시간이 걸린다.
반대로 $c$가 너무 작다면, 레이어가 크거나 BatchNorm을 쓰지 않는다면 쉽게 vanishing gradients 문제가 생길 수 있다.
clipping은 단순하지만 문제를 발생시킬 수 있다. 특히 $c$가 잘 정해지지 않았다면 품질이 낮은 이미지를 생성하고 수렴하지 않을 수 있다. 모델의 성능은 이 $c$에 매우 민감하다.
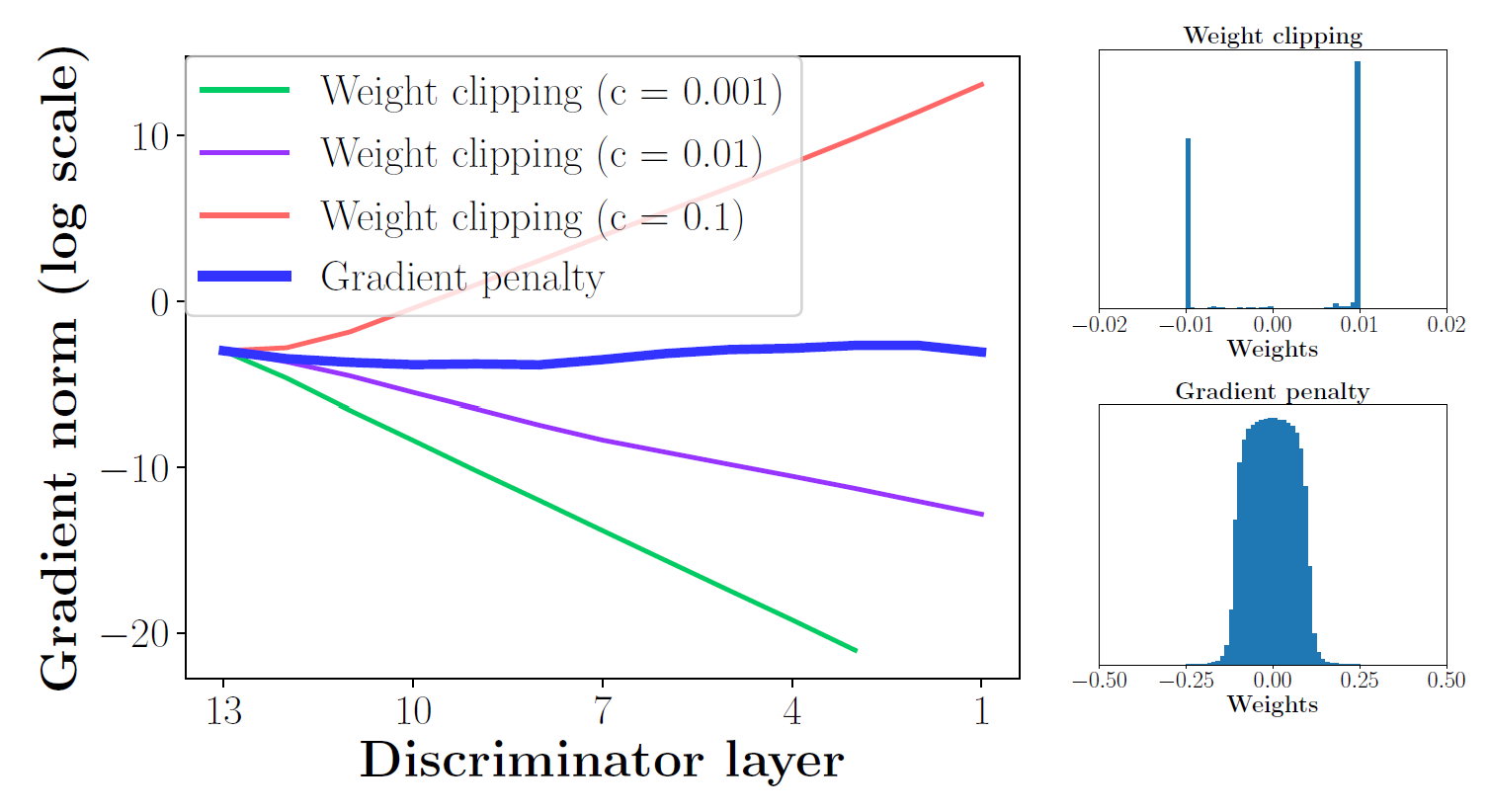
가중치 clipping은 가중치를 정규화하는 효과를 갖는다. 이는 모델 $f$의 어떤 한계치를 설정하는 것과 같다.
그래서 이 논문에서는 gradient penalty라는 것을 D의 목적함수에 추가해 이 한계를 극복하고자 한다(G의 목적함수는 건드리지 않은 듯 하다).
[L = \mathbb{E}{\hat{x} \sim \mathbb{P}_g} \ [D(\hat{x})] - \mathbb{E}{x \sim \mathbb{P}r} \ [D(x)] + \lambda \ \mathbb{E}{\hat{x} \sim \mathbb{P}{\hat{x}}} \ [(\Vert \nabla{\hat{x}}D(\hat{x}) \Vert_2 - 1)^2 ]]
즉 clipping을 적용하는 대신 WGAN_GP는 gradient norm이 목표인 $1$에서 멀어지면 penalty를 주는 방식을 택했다.
- Sampling Distribution: $\mathbb{P}_{\hat{x}}$는 실제 데이터 분포 $\mathbb{P}_r$과 G가 생성한 데이터 분포 $\mathbb{P}_g$로부터 추출한 point 쌍들 사이에 직선을 하나 그어서 얻은 것이다.
- Penalty coefficient: $\lambda$가 붙은 마지막 항(이 논문에서는 $\lambda=10$으로 고정됨)이 gradient penalty이다.
- No critic batch normalization: BN은 D의 문제의 형식을 1-1 매칭 문제에서 전체 batch input-batch output으로 바꿔버린다. 이 논문에서 새로 만든 gradient penalty 목적함수는 이 조건에 맞지 않기 때문에 BN을 쓰지 않았다.
- Two-sided penalty: gradient가 단지 $1$ 아래로 내려가는 것을 막는(one-sided) 대신 $1$ 근처에 머무르도록 했다(two-sided).
그래서 발전시킨 알고리즘은 다음과 같다.

좀 특이하게도 이 논문에는 모델 구조(architecture)를 바꿔가면서 한 실험 결과가 있다. 확실히 WGAN_GP 버전이 뛰어남을 볼 수 있다.

WGAN_GP만이 (이 논문에서 실험한) 모든 architecture에 대해서 제대로 된 학습에 성공하였다고 한다.

여러 실험 결과들이 더 있지만 하나만 더 소개하면,
논문에서는 아래 이미지(LSUN-bedroom)가 지금까지의 연구에 의해 나온 것 중 제일 잘 나온 것이라고 믿는다고 한다. 각각의 이미지가 $128 \times 128 $ 크기라 그다지 고해상도는 아니긴 하지만 어쨌든 실제로 꽤 깨끗한 이미지로 보인다.

[\]
종합하면 이 개선된 버전은 데이터셋뿐만 아니라(WGAN) 모델 구조에 대해서도(architecture) 학습 안정성을 얻었다고 할 수 있다.
DRAGAN
논문 링크: DRAGAN
2017년 5월 처음 제안되었다.
소스코드: tensorflow, pytorch
참고할 만한 사이트: 링크
WGAN_GP 논문과 차이점은 D(critic network)에 의해 계산되는 식별함수 $f$가 gradient에 있어 어떤 제한을 받는가이다.
- WGAN_GP에서는 gradient가 실제 데이터와 가짜 데이터 사이의 직선 위 랜덤한 곳으로 설정되기 때문에 모든 곳에서 $ \vert \nabla f \vert = 1 $를 향한다.
- DRAGAN에서는 gradient가 실제에 “가깝게” sampling된다. 이는 실제 데이터 근처에 있을 때만 $ \vert \nabla f \vert = 1 $를 향한다.
아래 그림은 위 차이를 보여준다. 참고 사이트에서 가져왔다.
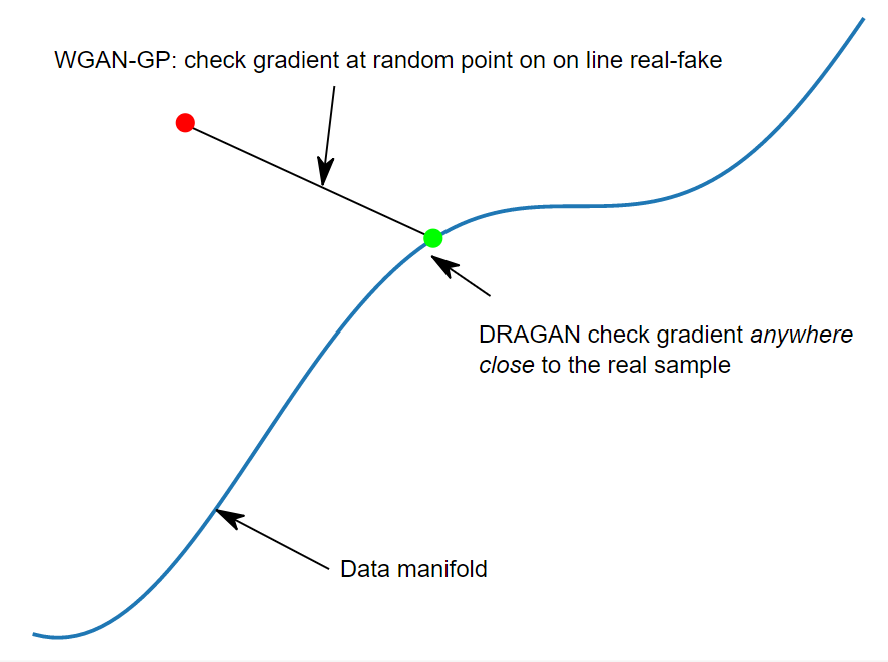
간단히 DRAGAN은 실제 데이터 분포(manifold)에 가까울 때만 gradient penalizing을 시켜 mode collapsing을 막을 수 있다.
$ \lambda $가 penalty hyperparameter로 사용되는데, 작은 $\lambda$는 toy tasks에 있어 특히 잘 학습됨을 볼 수 있다.
이 논문이 기여한 바는 다음과 같다:
- AGD를 regret minimization으로 봄으로써 GAN 학습에 대한 추론을 제안하였다.
- nonparametric 한계 안에서 GAN 학습의 점근적 수렴과 매 단계마다 D가 최적이어야 할 필요가 없다는 것을 증명하였다.
- AGD가 비 볼록(non-convex) 게임에서 잠재적으로 어떻게 나쁜 국소평형 지점(local minima)으로 수렴하는지와 이것이 GAN의 학습에 있어 mode collapsing에 얼마나 큰 책임이 있는지를 논했다.
- 실제 데이터에 근접한 경우에 D의 $f$의 gradient가 큰 값을 가질 때 어떻게 mode collapse 상황이 생기는지를 특징지었다.
- 이러한 관찰에 의해 DRAGAN(a novel gradient penalty scheme)을 소개하였고 이것이 mode collapsing 문제를 완화해준다는 것을 보였다.
원래의 GAN들은, sample이 real data에 가까움에도 sharp gradient를 갖기 떄문에 mode collapse의 정의에 의해 이것이 나타난다. 이러한 sharp gradient는 G가 많은 $z$ 벡터들을 하나의 출력값 $x$로 가게끔 하고 따라서 형평성(equilibrium, mode collapse의 정의를 생각하라)을 약화시키도록 한다.
그래서 이러한 실패를 막으려면 D에게 다음과 같은 penalty를 줘서 gradient를 정규화시키는 것이다:
[\lambda \ \cdot \ \mathbb{E}{x \sim P{real}, \ \delta \sim N_d (0, \ cI)} [\Vert \nabla_X D_\theta(x+\delta) \Vert^2 ]]
이 전략은 GAN 학습의 안정성을 증가시킨다. 이 논문에는 그 결과와 그렇게 되는 이유가 설명되어 있으니 자세한 부분은 이를 참고하자.
그러나, 이 논문에서는 위의 penalty 식이 여전히 불안정하며 지나치게 penalty를 주는(over-penalized) 경우가 있을 수 있고, 따라서 D는 real point $x$와 noise인 $x+\lambda$에게 동일한 “실제 데이터일” 확률을 부여할 수 있다는 것을 발견하였다. 따라서 더 나은 gradient penalty 식은
[\lambda \ \cdot \ \mathbb{E}{x \sim P{real}, \ \delta \sim N_d (0, \ cI)} [ \ max(0, \ \Vert \nabla_X D_\theta(x+\delta) \Vert^2 - k )\ ]]
그리고, 실험적인 최적화를 적용한 최종 penalty 식은
[\lambda \ \cdot \ \mathbb{E}{x \sim P{real}, \ \delta \sim N_d (0, \ cI)} [ \ \Vert \nabla_X D_\theta(x+\delta) \Vert - k \ ]^2]
결과적으로 real data의 작은 동요(변화, perturbations)에도 잘 작동하였다.
이 논문에서 사용한 gradient penalty schemes 또는 heuristics는 DRAGAN algorithm으로 부르기로 하였다.
EBGAN
2016년 9월 처음 제안되었다.
논문 링크: EBGAN
이 논문에서는 D를 data manifold에 가까운 지점에서는 낮은 에너지를, 그렇지 않은 지점에서는 높은 에너지를 갖도록 하는 일종의 energy function으로 보는 Energy-Based GAN을 소개한다. 일반 GAN과 비슷하게 G는 최대한 낮은 에너지를 갖는(즉, 실제 데이터와 비슷한) sample을 생성하고, D는 G가 생성한 이미지들에는 높은 에너지를 부여하도록 한다.
D를 energy function으로 봄으로써 다양한 architecture과 loss function에 사용할 수 있게 되었다. 이 논문에서는 D를 auto-encoder로 구현하였다.
결과적으로 EBGAN은 학습이 더 안정적이며 또한 고해상도 이미지를 생성하는 데에도 능하다는 것을 보여주었다.
우선 Energy Based Model은,
- LeCun이 2006년 제안하였으며
- input space를 하나의 scalar(energy로 지칭된다)로 mapping하는 모델이다.
- 학습이 제대로 된 경우 낮은 에너지를, 아니면 높은 에너지를 생성하며
- CNN등의 학습에서 cross entropy loss를 사용하여 loss를 낮춰가는 것과 비슷하다. 여기선 loss랑 energy랑 비슷하게 사용된다.
간단히 이 Energy Based Model을 GAN에 적용시킨 것이 EBGAN이다.
이 논문의 contribution은,
- GAN 학습에 energy-based를 적용시켰고
- simple hinge loss에 대해, 시스템이 수렴했을 때 G는 데이터 분포를 따르는 point를 생성하게 된다는 증명과
- energy를 reconstruction error로 본 auto-encoder architecture로 EBGAN framework를 만들었고
- EBGAN과 확률적 GAN 모두에게 좋은 결과를 얻을 수 있는 시스템적 실험셋(hyperparameter 등)
- ImageNet 데이터셋에 대해 256$\times$256 고해상도 이미질르 생성할 수 있음을 보여주었다.
목적함수는 다음과 같이 정의된다. $[\cdot]^+ = max(0,\ \cdot)$이다.
[\mathcal{L}_D(x, z) = D(x) + [m - D(G(z))]^{+}]
[\mathcal{L}_G(z) = D(G(z))]
EBGAN은 per-pixel Euclidean distance를 사용한다.
찾아낸 해가 optimum인지에 대한 증명은 Theorem 1과 2로 나누어져 증명이 논문에 수록되어 있다. 간략히 소개하기엔 꽤 복잡하므로 넘어간다.
D의 구조를 나타내면 다음과 같다.
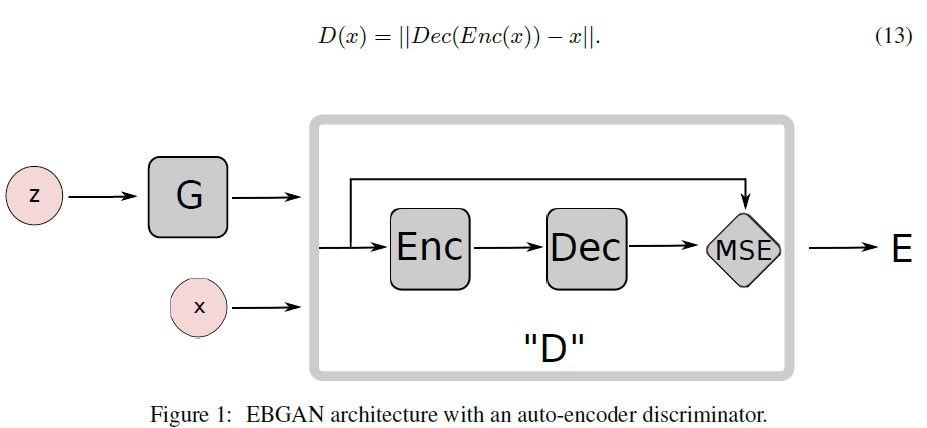
왜 auto-encoder를 썼냐 하면:
- D가 오직 0과 1 두 값만 낸다면 한 minibatch 안에서 많은 다른 sample들이 orthogonal에서 멀어질 것임을 뜻한다. 이는 비효율적인 학습을 초래하며, minibatch size를 줄이는 것은 현재 하드웨어 상으로 별로 좋은 옵션이 아니다. 그래서 이 대신 reconstruction-based output을 씀으로써 D에게 좀 더 다양한 target을 제공한다.
- Auto-encoder는 전통적으로 energy-based model을 표현하는 좋은 모델이다. auto-encoder는 supervision이나 negative sample 같은 것 없이도 energy manifold를 잘 학습할 수 있다. 이는 EBGAN auto-encoding model이 실제 데이터를 복원하도록 학습했을 때, D는 그 data manifold를 스스로 찾아낼 수 있다는 뜻이다. 반대로 G로부터의 negative sample이 없다면 binary logistic loss로 학습된 D는 무의미하다는 뜻이기도 하다.
이 논문에서는 repelling regularizer라는 것을 제안하는데, 이는 모델이 겨우 몇 개의 $p_{data}$로 뭉쳐 있는 sample들을 생성하는 것을 고의로 막기 위한 것으로 EBGAN auto-encoder model에 최적화된 것이다.
Pulling-away Term, PT는 다음과 같이 정의된다:
[f_{PT}(S) = \frac{1}{N(N-1)} \sum_i \sum_{j \ne i} \Bigl( \frac{S_i S_j}{\Vert S_i \Vert \Vert S_j \Vert } \Bigr)^2]
PT는 minibatch 상에서 동작하고 쌍으로 sample representation을 orthogonalize하려고 한다. 논문에서는 PT로 학습된 EBGAN auto-encoder model을 EBGAN-PT라고 부르기로 하였다.
이 논문의 실험결과는 다른 GAN과는 약간 다르다. Inception score를 생성 품질을 측정하는 척도로 사용하여 GAN과 EBGAN의 생성 품질을 비교한 것이다. 점수가 높을수록 품질이 좋은 것이도, 각 막대그래프는 해당 점수를 가진 sample의 비율이 얼마나 되는지를 나타낸 것이다. 따라서 각 막대가 오른쪽에 많이 분포할수록 생성 품질이 좋다고 할 수 있다.
아래 그림은 일부만 가져온 것이다. 논문에서도 그림이 너무 작으니 pdf에서 확대해서 보라는 것을 추천하고 있다. 그림이 15개 정도 있는데, 실험 조건만 다를 뿐 대부분 비슷한 분포를 보이고 있다.
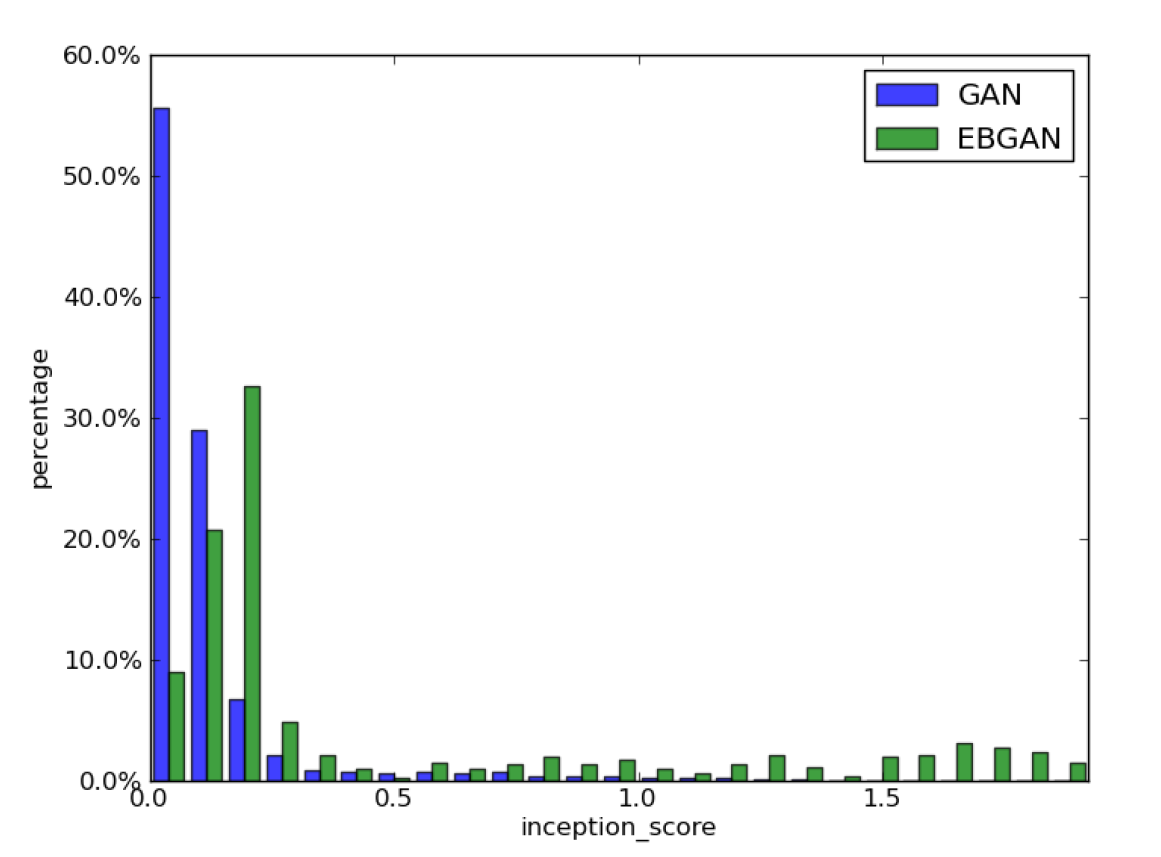
일반 GAN과 비교하면 MNIST 생성 품질도 확실히 좋은 것을 볼 수 있다.

또 LSUN, CELEBA, ImageNet 데이터셋에 대해서도 실험한 결과들이 논문에 실려 있다. 대부분의 이미지는 품질이 훨씬 좋고 선명한 이미지 품질을 볼 수 있다.
BEGAN
논문 링크: BEGAN
2017년 3월 처음 제안되었다.
구글이 내놓은 GAN 논문이다. 이 논문에서 중요한 특징 및 개선점은,
- 모델 구조는 더 단순해졌고, 여전히 빠르고 안정적인 학습이 가능하다.
- EBGAN을 바탕으로 해 energy와 auto-encoder를 사용한다. 다만 loss는 WGAN의 Wasserstein distance를 사용한다.
- 대부분의 GAN이 ‘실제 데이터 분포’와 ‘가짜 데이터 분포’ 사이의 거리를 좁히기 위해 노력해왔다면, BEGAN은 ‘진짜 데이터에 대한 auto-encoder 데이터 분포’와 ‘가짜 데이터에 대한 auto-encoder 데이터 분포’ 사이의 거리를 계산한다.
- D가 G를 압도하는 상황이 발생하는 것을 막기 위해 D와 G의 equilibrium을 조절하는 hyperparameter $\gamma$를 도입하였다. diversity ratio라고 부른다는데, 이것으로
- auto-encoder가 데이터를 복원하는 것과 진짜/가짜를 구별하는 것 사이의 균형을 맞추고
- $\gamma$가 낮으면 auto-encoder가 새 이미지를 생성하는 것에 집중한다는 것이므로 이미지 다양성이 떨어진다. 반대는 당연히 반대의 효과를 가진다.
- 이 equilibrium 개념을 가져와서 수렴(즉, 학습)이 잘 되었는지를 판별하는 데 쓸 수도 있다.
이 논문은 결과에 비해 수식이 꽤 단순한 편이다.
auto-encoder의 Wasserstein distance 하한
우선 pixel-wise auto-encoder를 학습할 때 $ \mathcal{L}: \mathbb{R}^{N_x} \mapsto \mathbb{R}^+$ 를 정의하면,
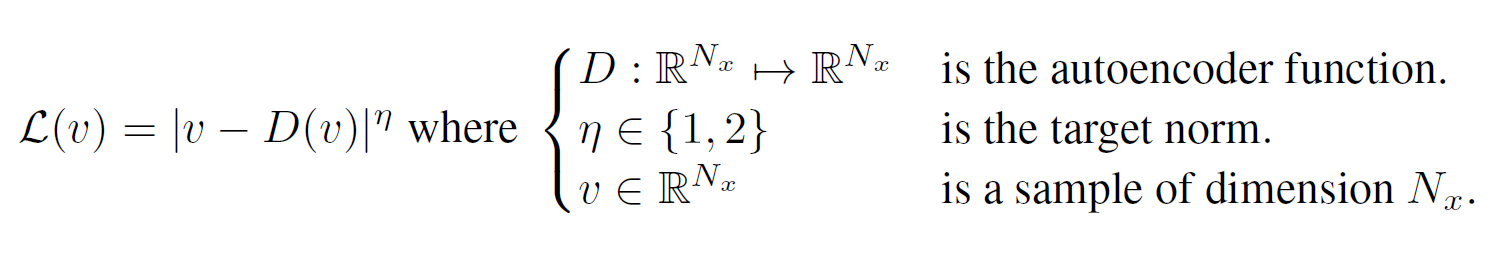
$\mu_{1, 2}$를 auto-encoder loss의 두 분포라 하고, $\Gamma(\mu_1, \mu_2)$를 모든 $\mu_1$과 $\mu_2$의 결합들의 집합이라 하고, $m_{1, 2} \in \mathbb{R}$을 각 평균이라 하면, Wasserstein distance는
[W_1(\mu_1, \mu_2) = inf_{\gamma \in \Gamma(\mu_1, \mu_2)} \ \mathbb{E}_{(x_1, x_2) \sim \gamma} [\vert x_1 - x_2 \vert ]]
Jensen’s inequality를 써서
[inf \mathbb{E}[ \vert x_1 - x_2 \vert ] \geqslant inf \vert \mathbb{E}[x_1 - x_2] \vert = \vert m_1 - m_2 \vert]
데이터 분포 간 사이의 거리를 구하려는 것이 아니라 auto-encoder loss distribution의 Wasserstein distance를 구하려고 하는 것이라는 것을 알아둘 필요가 있다.
GAN의 목적함수에서, $\vert m_1 - m_2 \vert $를 최대화하는 것은 딱 두 가지인데, $m_1$이 0으로 가는 것이 auto-encoder가 실제 이미지를 생성하는 것으로 자연스럽기 때문에 선택한 것은 다음 중 (b)이다.
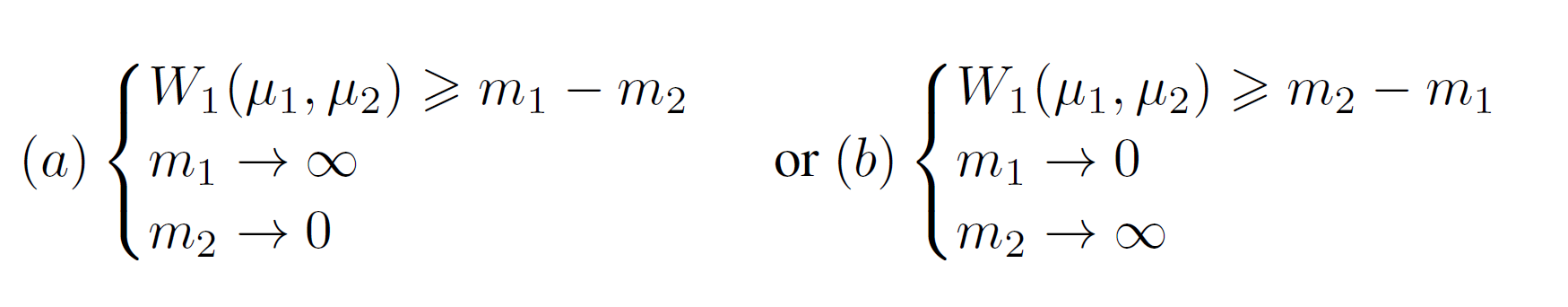
GAN의 목적함수를 정리하면,
[\mathcal{L}_D = \mathcal{L}(x;\theta_D) - \mathcal{L}(G(z_D;\theta_G);\theta_D) \qquad \text{for} \ \ \theta_D]
[\mathcal{L}_G = -\mathcal{L}_D \qquad \qquad \qquad \qquad \qquad \qquad \text{for} \ \ \theta_G]
참고: $ G(\cdot) = G(\cdot, \ \theta_G), \mathcal{L}(\cdot) = \mathcal{L}(\cdot ; \ \theta_D)$이다.
D와 G의 평형(equilibrium)
만약 평헝이 이루어졌다면 다음은 당연하다:
[\mathbb{E} [ \mathcal{L}(x)] = \mathbb{E}[\mathcal{L}(G(z))]]
한쪽이 지나치게 강해지는 것을 막기 위해, diversity ratio $\gamma$를 정의하였다:
[\gamma = \frac{\mathbb{E}[\mathcal{L}(G(z))]}{ \mathbb{E}[\mathcal{L}(x)] } \in [0, 1]]
이것으로 조금 위에서 말한 이미지의 다양성과 품질 간 trade-off, D와 G의 평형 등을 모두 얻을 수 있다.
BEGAN의 목적함수
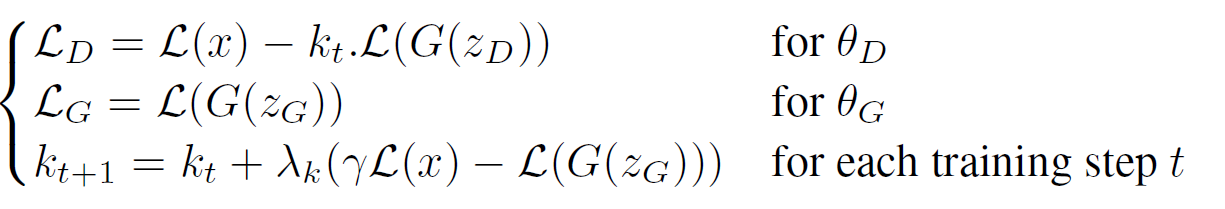
- $ \mathbb{E}[\mathcal{L}(G(z))] = \gamma \mathbb{E}[ \mathcal{L}(x)] $를 유지하기 위해 Proportional Control Theory를 사용하였다.
- $k_t \in [0, 1]$를 사용하여 얼마나 경사하강법 중 $\mathcal{L}(G(z))$를 강조할 것인지를 조절한다.
- $k_0 = 0$
- t가 지날수록 값이 커진다.
- $\lambda_k$는 learning rate와 비슷하다.
수렴 판별 방법
조금 전의 equilibrium 컨셉을 생각해서, 수렴과정을 가장 가까운 복원 $\mathcal{L}(x)$를 찾는 것으로 생각할 수 있다.
수렴 측정방법은 다음과 같이 표현 가능하다:
[\mathcal{M}_{global} = \mathcal{L}(x) + \vert \gamma \mathcal{L}(x) - \mathcal{L}(G(z_G)) \vert]
이는 모델이 잘 학습되어 최종 상태에 도달했는지, 아니면 mode collapsing했는지를 판별할 때 쓸 수 있다.
Model architecture
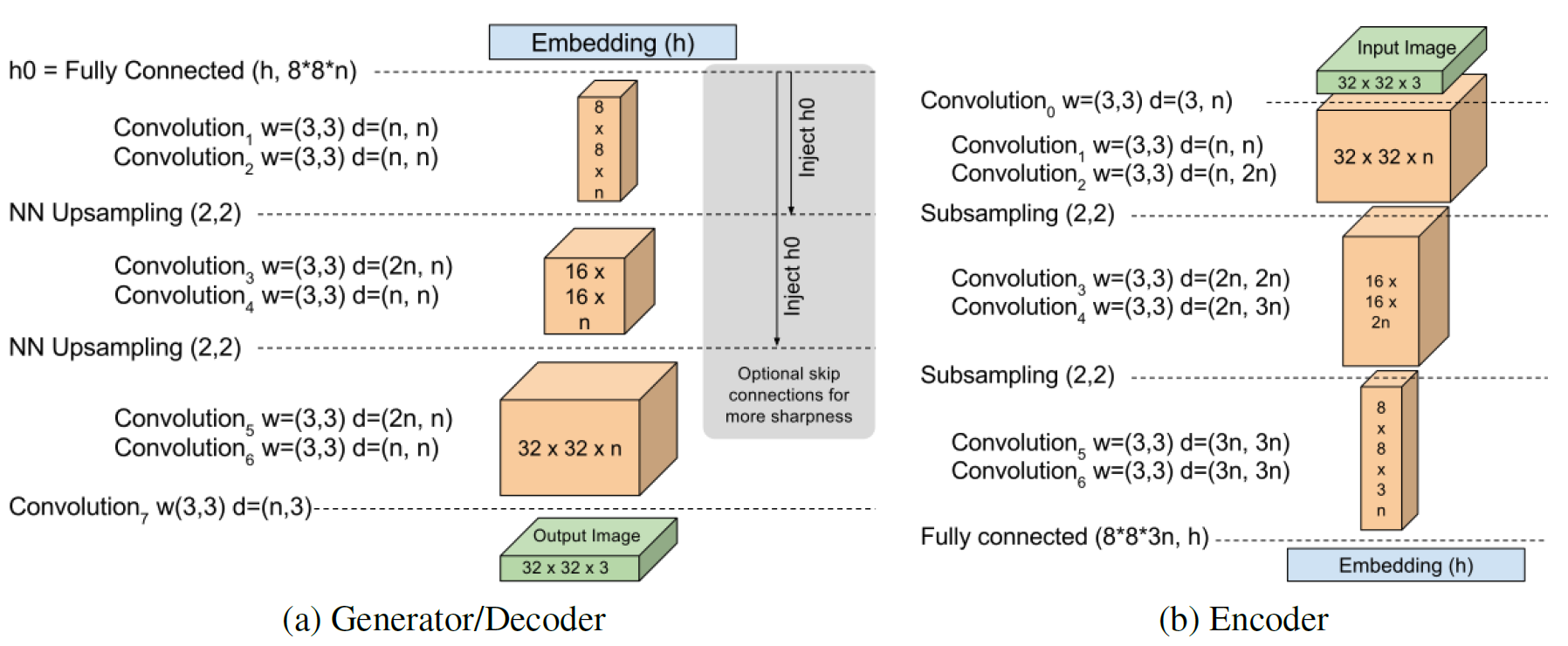
DCGAN과는 달리
- batch norm
- dropout
- transpose convolution
- exponential growth for convolution filters
등이 다 없다. 모델 구조가 상당히 단순함을 알 수 있다.
실험 결과
간단히 말하면..좋다.

예전에 DCGAN에서 봤던 interpolating도 잘 됨을 확인할 수 있다.

ACGAN
논문 링크: ACGAN
2016년 10월 처음 제안되었다.
DCGAN에서는 $z$가 속한 벡터공간의 각 차원별 특징은 사람이 해석할 수 없는 수준이다. 즉 $z$의 요소를 변화시킬 때 사진이 변화하는 형상은 알 수 있지만, 각각의 차원이 정확히 무슨 역할을 하고 어떤 특징을 갖는지는 알 수가 없다.
그러나 해석하기 쉬운 특징량(disentangled latend code)에 의존하는 모델들이 여럿 제안되었는데, 그것은 앞에서 설명했던 CGAN, ACGAN, infoGAN 등이 있다.
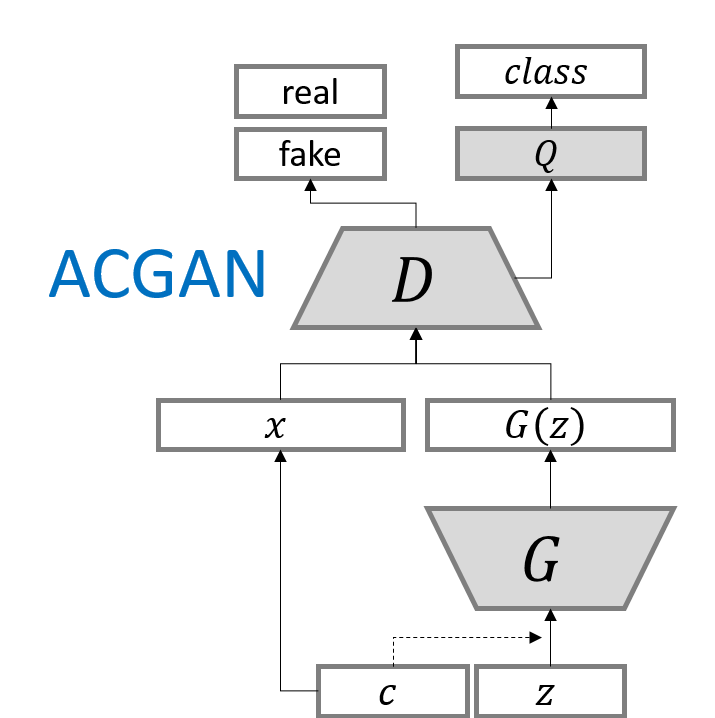
ACGAN이 original GAN 및 CGAN과 다른 점은,
- D는 2개의 분류기로 구성되는데
- 하나는 original GAN과 같은 real/fake 판별
- 다른 하나는 데이터의 class 판별
- 목적함수: 맞는 Source의 log-likelihood $L_S$, 맞는 Class의 log-likelihood $L_C$ 두 개로 나누어
- $L_S$는 기존 GAN의 목적함수와 같다. 즉 real/fake를 판별하는 것과 관련이 있다.
- $L_C$는 그 데이터의 class를 판별하는 것과 관련이 있다. CGAN에서 본 것과 약간 비슷하다.
- D는 $L_S+L_C$를 최대화하고
- G는 $L_C-L_S$를 최대화하도록 학습된다.
[L_S = E[log \ p(S=real \vert X_{real})] + E[log \ p(S=fake \vert X_{fake})]]
[L_C = E[log \ p(C=c \quad \ \vert X_{real})] + E[log \ p(C=c \ \ \quad \vert X_{fake})]]
실험은 ImageNet과 CIFAR-10에 대해 진행하였다고 한다. 결과는 (위의 BEGAN에 비해) 아주 놀랍지는 않아서(물론 예전 논문이다) 생략한다.
대신 실험 시 사용한 모델 구조를 가져왔다.
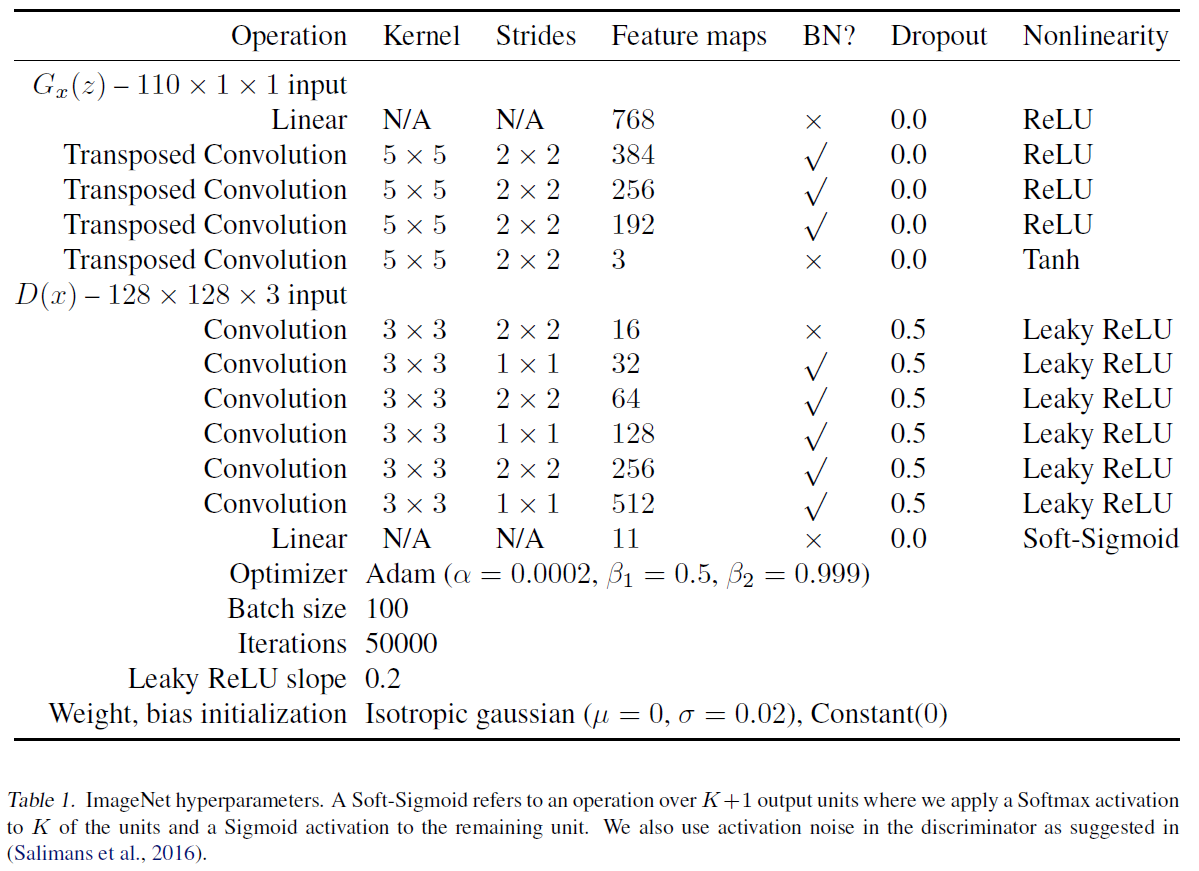
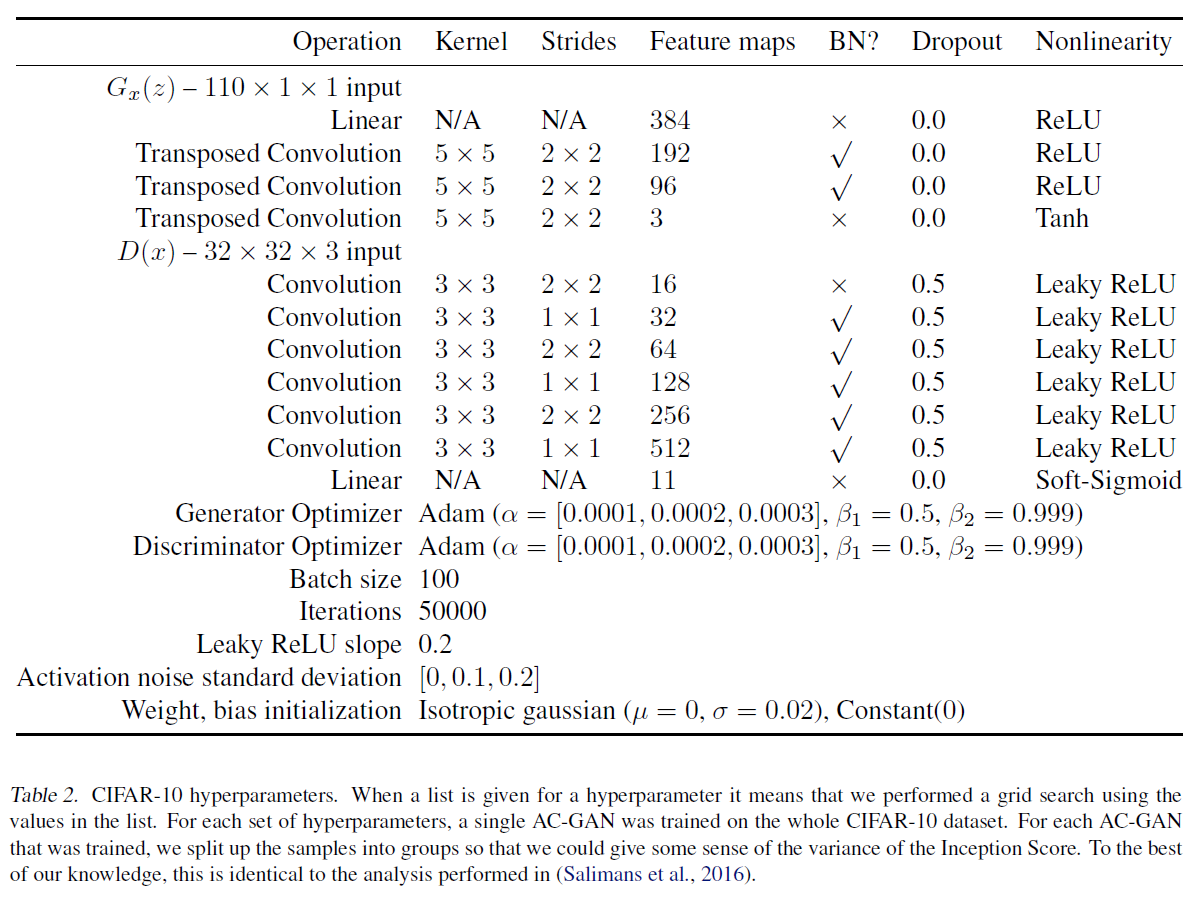
infoGAN
논문 링크: infoGAN
2016년 6월 처음 제안되었다.
original GAN은 input vector $z$에 어떠한 제한도 없이 단순히 무작위 값을 집어넣었기 때문에, 이러한 $z$의 각 차원은 역할이 분리되지 않고 심하게 꼬여(entangled) 있다.
그러나 이 domain들은 서로 다른 역할을 하는 여러 부분으로 분리될 수 있다.
그래서 이 논문에서는 noise 부분 $z$와, 데이터 분포의 가장 중요한 의미를 가지는 특징량(latent code) $c$ 두 부분으로 나누었다(CGAN과 비슷). 특징량은 설명 가능한 부분(semantic features), $z$는 원래의 것처럼 데이터를 생성하기 위한 incompressible noise이다.
G에 들어가는 input은 따라서 $G(z, c)$로 표시된다. 그러나 기존 GAN은 단지 $P_G(x \vert c) = P_G(x)$로 처리함으로써 특징량 $c$를 무시해버릴 수 있다. 따라서 정보이론적 정규화를 시행하도록 한다: $c$와 $G(z, c)$ 사이에는 아주 높은 상호정보량이 있기 때문에, $I(c;\ G(z,c))$ 역시 높을 것이다.
참고: 상호정보량은 다음과 같이 KLD로 측정한다. 서로 독립인 경우 0이 되는 것은 상호정보량의 이름에서 봤을 때 직관적이다.
[I(X;Y) = D_{KL}(p(x,y) \Vert p(x)p(y))]
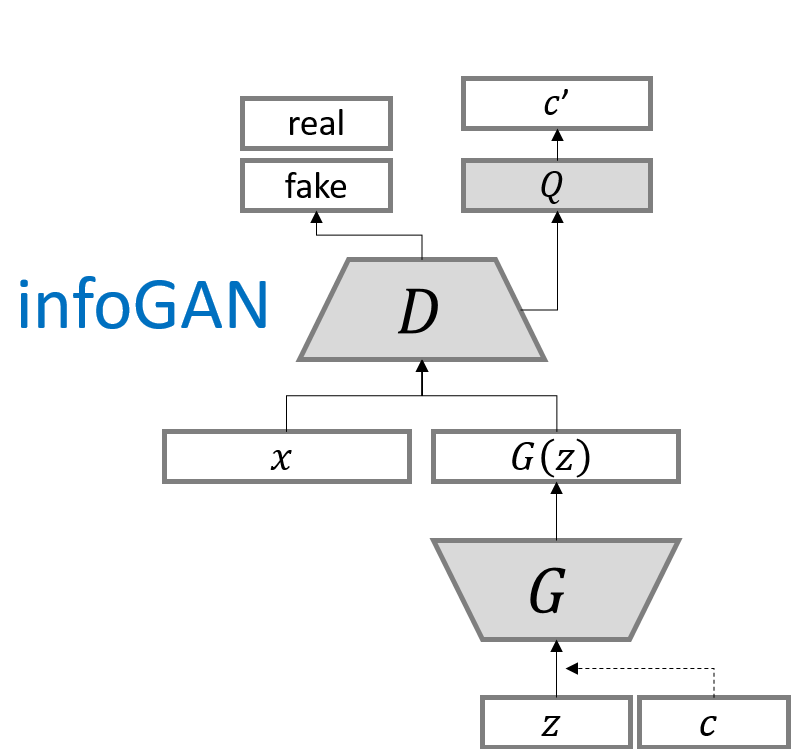
그래서 목적함수는 다음과 같다.
[min_G max_D V_I(D, G) = V(D, G) - \lambda I(c; G(z, c))]
$V(D, G)$는 기존 GAN의 목적함수이다.
상호정보량은 쉽게 구하긴 어렵기 때문에, 논문에서는 이를 직접적으로 구하는 대신 하한을 구해 이를 최대화하는 방식을 썼다. 수식을 중간과정을 일부 생략하고 적으면
[I(c; G(z, c)) = H(c) - H(c \vert G(z, c)) = \mathbb{E}{x \sim G(z,c)} [ \mathbb{E}{c’ \sim P(c \vert x)}[log \ P(c’ \vert x)]] + H(c)]
[\qquad \qquad \qquad \qquad \qquad \qquad \qquad \quad \ \ \ge \mathbb{E}{x \sim G(z,c)} [ \mathbb{E}{c’ \sim P(c \vert x)}[log \ Q(c’ \vert x)]] + H(c)]
상호정보량 I(c; G(z, c))의 variational lower bound $L_I(G, Q)$를 정의할 수 있는데,
[L_I(G, Q) = E_{c \sim P(c), x \sim G(z, c)}[log \ Q(c \vert x)] + H(c)]
[\qquad \qquad \qquad \ = E_{x \sim G(z,c)} [ \mathbb{E}_{c’ \sim P(c \vert x)}[log \ Q(c’ \vert x)]] + H(c)]
[\le I(c; G(z, c)) \ \qquad \qquad \quad]
그래서 infoGAN은 아래 minimax game을 하는 것이 된다:
[min_{G, Q} max_D V_{\text{infoGAN}}(D, G, Q) = V(D, G) - \lambda L_I(G,Q)]
실험 결과
semantic features $c$를 적절히 조작하면 생성될 이미지에 어떤 변화를 줄 수 있는지를 중점적으로 보여주었다.
MNIST의 경우 숫자의 종류(digit), 회전, 너비 등을 조작할 수 있고, 사람 얼굴의 경우 얼굴의 각도, 밝기, 너비 등을 바꿀 수 있음을 보여주었다.


더 많은 결과는 논문을 참조하자.
이후 연구들
GAN 이후로 수많은 발전된 GAN이 연구되어 발표되었다.
GAN 학습에 관한 내용을 정리한 것으로는 다음 논문이 있다. Improved Techniques for Training GANs
또 다른 것으로는 PROGDAN, SLOGAN 등이 있다.