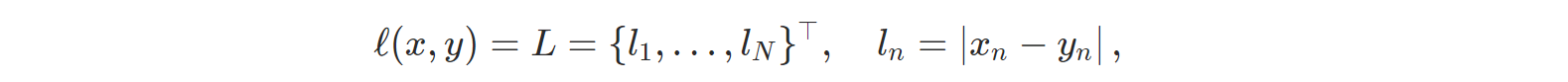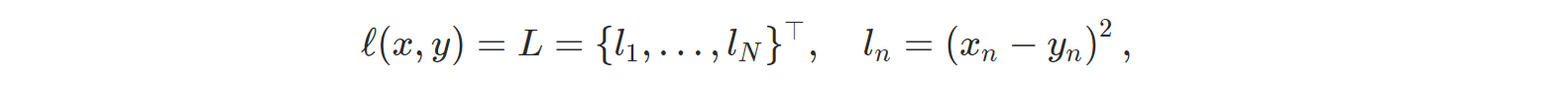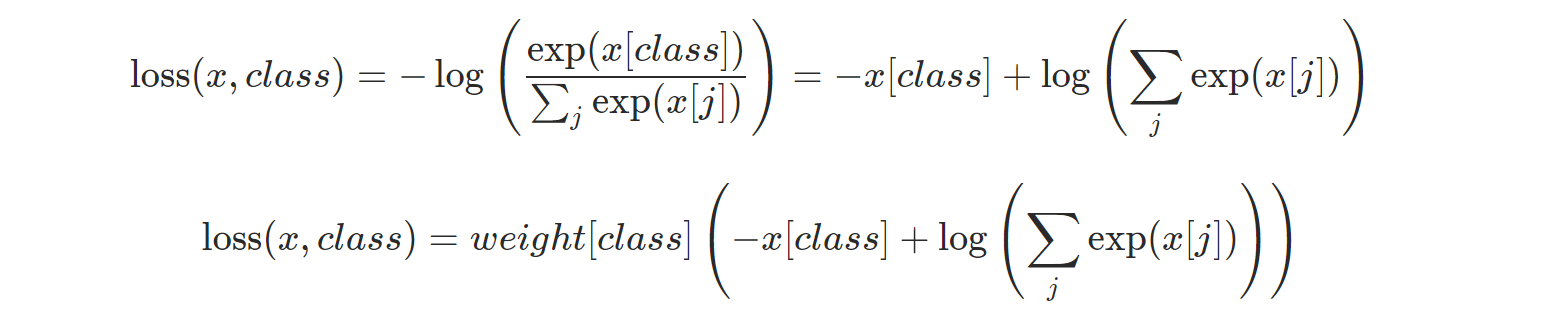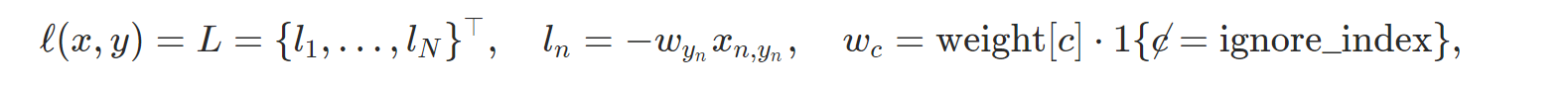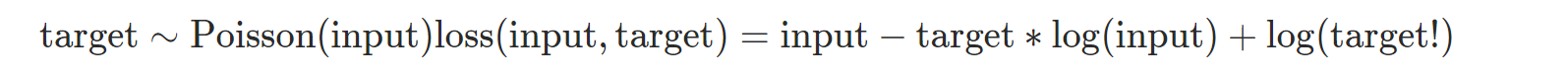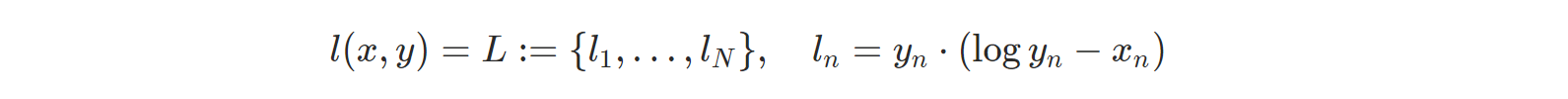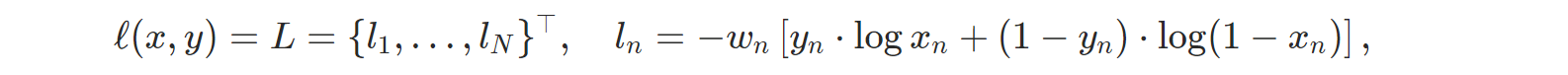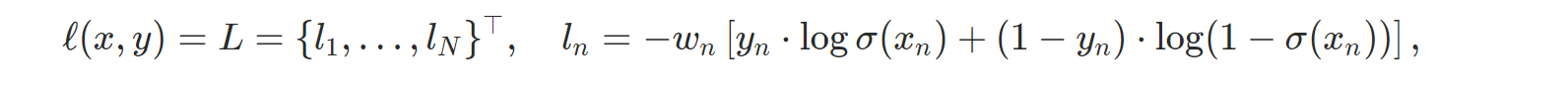PyTorch 사용법 - 03. How to Use PyTorch
10 Nov 2018 | PyTorchPyTorch 사용법 - 00. References
PyTorch 사용법 - 01. 소개 및 설치
PyTorch 사용법 - 02. Linear Regression Model
PyTorch 사용법 - 03. How to Use PyTorch
2020.02.04 Updated
이 글에서는 PyTorch 프로젝트를 만드는 방법에 대해서 알아본다.
사용되는 torch 함수들의 사용법은 여기에서 확인할 수 있다.
Pytorch의 학습 방법(loss function, optimizer, autograd, backward 등이 어떻게 돌아가는지)을 알고 싶다면 여기로 바로 넘어가면 된다.
Pytorch 사용법이 헷갈리는 부분이 있으면 Q&A 절을 참고하면 된다.
예시 코드의 많은 부분은 링크와 함께 공식 Pytorch 홈페이지(pytorch.org/docs)에서 가져왔음을 밝힌다.
주의: 이 글은 좀 길다. ㅎ
Import
# preprocess, set hyperparameter
import argparse
import os
# load data
from torch.utils.data import DataLoader
from torchvision import datasets, transforms
# train
from torch import nn
from torch.nn import functional as F
# visualization
import matplotlib.pyplot as plt
argparse
python train.py --epochs 50 --batch-size 64 --save-dir weights
Machine Learning을 포함해서, 위와 같은 실행 옵션은 많은 코드에서 볼 수 있었을 것이다. 학습 과정을 포함하여 대부분은 명령창 또는 콘솔에서 python 파일 옵션들...으로 실행시키기 때문에, argparse에 대한 이해는 필요하다.
argparse에 대한 내용은 여기를 참조하도록 한다.
Load Data
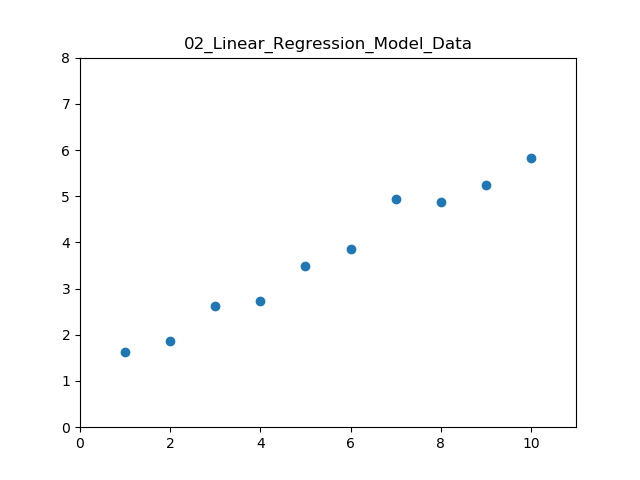
전처리하는 과정을 설명할 수는 없다. 데이터가 어떻게 생겼는지는 직접 봐야 알 수 있다.
다만 한 번 쓰고 말 것이 아니라면, 데이터가 추가되거나 변경점이 있더라도 전처리 코드의 대대적인 수정이 발생하도록 짜는 것은 본인 손해이다.
단순한 방법
data = pd.read_csv('data/02_Linear_Regression_Model_Data.csv')
# Avoid copy data, just refer
x = torch.from_numpy(data['x'].values).unsqueeze(dim=1).float()
y = torch.from_numpy(data['y'].values).unsqueeze(dim=1).float()
pandas나 csv 패키지 등으로 그냥 불러오는 방법이다. 데이터가 복잡하지 않은 형태라면 단순하고 유용하게 쓸 수 있다. 그러나 이 글에서 중요한 부분은 아니다.
torch.utils.data.DataLoader
참조: torch.utils.data.DataLoader
Pytorch는 DataLoader라고 하는 괜찮은 utility를 제공한다. 간단하게 생각하면 DataLoader 객체는 학습에 쓰일 데이터 전체를 보관했다가, train 함수가 batch 하나를 요구하면 batch size 개수만큼 데이터를 꺼내서 준다고 보면 된다.
- 실제로
[batch size, num]처럼 미리 잘라놓는 것은 아니고, 내부적으로 Iterator에 포함된 Index가 존재한다. train() 함수가 데이터를 요구하면 사전에 저장된 batch size만큼 return하는 형태이다.
사용할 torch.utils.data.Dataset에 따라 반환하는 데이터(자연어, 이미지, 정답 label 등)는 조금씩 다르지만, 일반적으로 실제 DataLoader를 쓸 때는 다음과 같이 쓰기만 하면 된다.
for idx, (data, label) in enumerate(data_loader):
...
DataLoader 안에 데이터가 어떻게 들어있는지 확인하기 위해, MNIST 데이터를 가져와 보자. DataLoader는 torchvision.datasets 및 torchvision.transforms와 함께 자주 쓰이는데, 각각 Pytorch가 공식적으로 지원하는 dataset, 데이터 transformation 및 augmentation 함수들(주로 이미지 데이터에 사용)를 포함한다.
각각의 사용법은 아래 절을 참조한다.
input_size = 28
batch_size = 64
transform = transforms.Compose([transforms.Resize((input_size, input_size)),
transforms.ToTensor()])
data_loader = DataLoader(
datasets.MNIST('data/mnist', train=True, download=True, transform=transform),
batch_size=batch_size,
shuffle=True)
print('type:', type(data_loader), '\n')
first_batch = data_loader.__iter__().__next__()
print('{:15s} | {:<25s} | {}'.format('name', 'type', 'size'))
print('{:15s} | {:<25s} | {}'.format('Num of Batch', '', len(data_loader)))
print('{:15s} | {:<25s} | {}'.format('first_batch', str(type(first_batch)), len(first_batch)))
print('{:15s} | {:<25s} | {}'.format('first_batch[0]', str(type(first_batch[0])), first_batch[0].shape))
print('{:15s} | {:<25s} | {}'.format('first_batch[1]', str(type(first_batch[1])), first_batch[1].shape))
결과:
type: <class 'torch.utils.data.dataloader.DataLoader'>
name | type | size
Num of Batch | | 938
first_batch | <class 'list'> | 2
first_batch[0] | <class 'torch.Tensor'> | torch.Size([64, 1, 28, 28])
first_batch[1] | <class 'torch.Tensor'> | torch.Size([64])
# 총 데이터의 개수는 938 * 28 ~= 60000(마지막 batch는 32)이다.
Custom Dataset 만들기
nn.Module을 상속하는 Custom Model처럼, Custom DataSet은 torch.utils.data.Dataset를 상속해야 한다. 또한 override해야 하는 것은 다음 두 가지다. python dunder를 모른다면 먼저 구글링해보도록 한다.
__len__(self): dataset의 전체 개수를 알려준다.__getitem__(self, idx): parameter로 idx를 넘겨주면 idx번째의 데이터를 반환한다.
위의 두 가지만 기억하면 된다. 전체 데이터 개수와, i번째 데이터를 반환하는 함수만 구현하면 Custom DataSet이 완성된다.
다음에는 완성된 DataSet을 torch.utils.data.DataLoader에 인자로 전달해주면 끝이다.
완전 필수는 아니지만 __init__()도 구현하는 것이 좋다.
1차함수 선형회귀(Linear Regression)의 예를 들면 다음과 같다.
데이터는 여기에서 받을 수 있다.
class LinearRegressionDataset(Dataset):
def __init__(self, csv_file):
"""
Args:
csv_file (string): Path to the csv file.
"""
data = pd.read_csv(csv_file)
self.x = torch.from_numpy(data['x'].values).unsqueeze(dim=1).float()
self.y = torch.from_numpy(data['y'].values).unsqueeze(dim=1).float()
def __len__(self):
return len(self.x)
def __getitem__(self, idx):
x = self.x[idx]
y = self.y[idx]
return x, y
dataset = LinearRegressionDataset('02_Linear_Regression_Model_Data.csv')
torchvision.datasets
Pytorch가 공식적으로 다운로드 및 사용을 지원하는 datasets이다. 2020.02.04 기준 dataset 목록은 다음과 같다.
- MNIST
- MNIST(숫자 0~9에 해당하는 손글씨 이미지 6만(train) + 1만(test))
- Fashion-MNIST(간소화된 의류 이미지),
- KMNIST(일본어=히라가나, 간지 손글씨),
- EMNIST(영문자 손글씨),
- QMNIST(MNIST를 재구성한 것)
- MS COCO
- Captions(이미지 한 장과 이를 설명하는 한 영문장),
- Detection(이미지 한 장과 여기에 있는 object들을 segmantation한 정보)
- LSUN(https://www.yf.io/p/lsun),
- ImageFolder, DatasetFolder
- Image:
- ImageNet 2012,
- CIFAR10 & CIFAR100,
- STL10, SVHN, PhotoTour, SBU
- Flickr8k & Flickr30k, VOC Segmantation & Detection,
- Cityscapes, SBD, USPS, Kinetics-400, HMDB51, UCF101
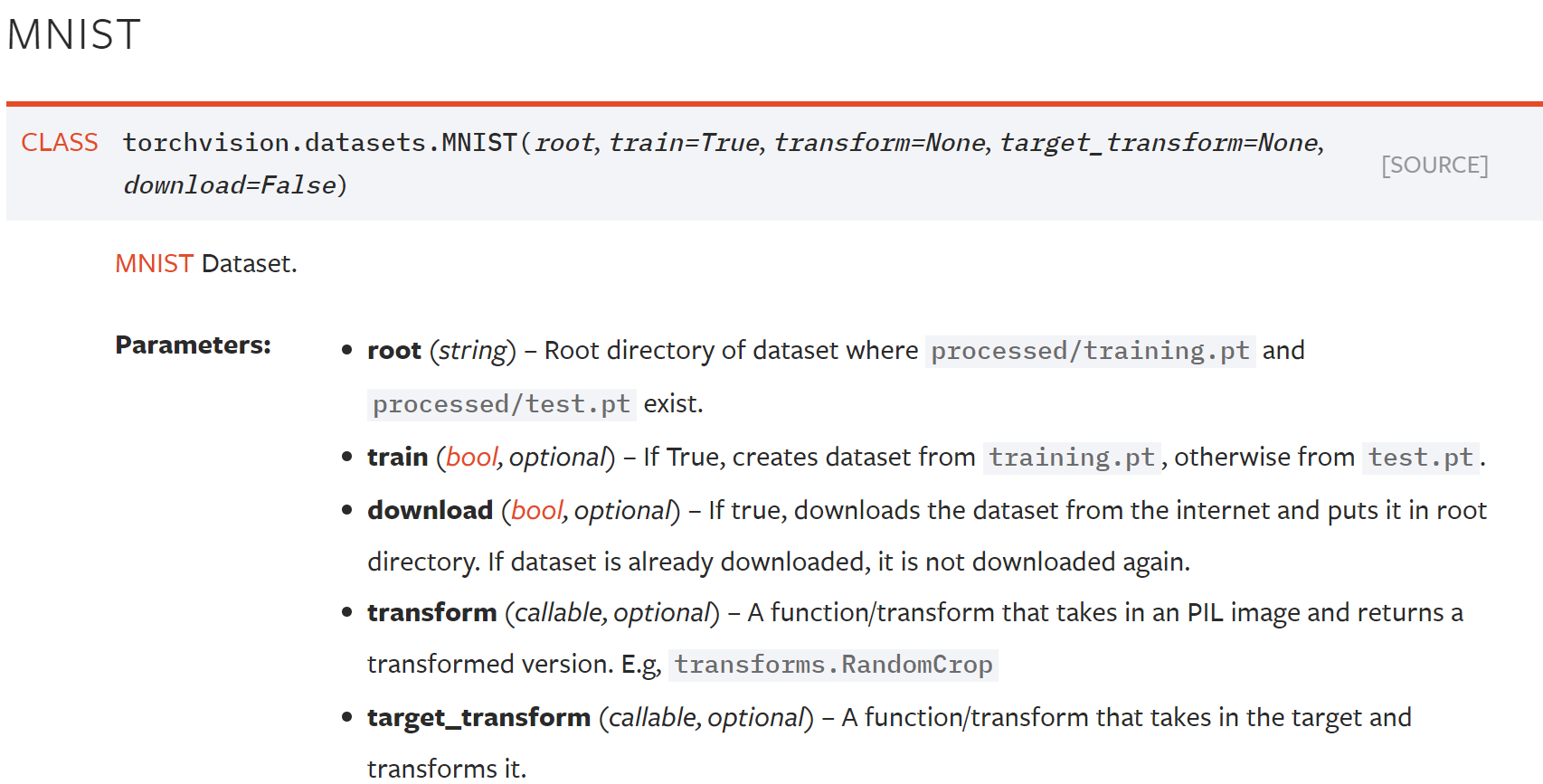
각각의 dataset마다 필요한 parameter가 조금씩 다르기 때문에, MNIST만 간단히 설명하도록 하겠다. 사실 공식 홈페이지를 참조하면 어렵지 않게 사용 가능하다.
- root: 데이터를 저장할 루트 폴더이다. 보통
data/나data/mnist/를 많이 쓰는 것 같지만, 상관없다. - train: 학습 데이터를 받을지, 테스트 데이터를 받을지를 결정한다.
- download: true로 지정하면 알아서 다운로드해 준다. 이미 다운로드했다면 재실행해도 다시 받지 않는다.
- transform: 지정하면 이미지 데이터에 어떤 변형을 가할지를 transform function의 묶음(Compose)로 전달한다.
- target_transform: 보통 위의 transform까지만 쓰는 것 같다. 쓰고 싶다면 이것도 쓰자.
torchvision.transforms
-
이미지 변환 함수들을 포함한다. 상대적으로 자주 쓰이는 함수는 다음과 같은 것들이 있다. 더 많은 목록은 홈페이지를 참조하면 된다. 참고로 parameter 중
transforms는 변환 함수들의 list 또는 tuple이다.- transforms.CenterCrop(size): 이미지의 중앙 부분을 크롭하여 [size, size] 크기로 만든다.
- transforms.Resize(size, interpolation=2): 이미지를 지정한 크기로 변환한다. 직사각형으로 자를 수 있다.
- 참고: transforms.Scale는 Resize에 의해 deprecated되었다.
- transforms.RandomCrop(size, padding=None, pad_if_needed=False, fill=0, padding_mode=’constant’): 이미지의 랜덤한 부분을 [size, size] 크기로 잘라낸다. input 이미지가 output 크기보다 작으면 padding을 추가할 수 있다.
- transforms.RandomResizedCrop(size, scale=(0.08, 1.0), ratio=(0.75, 3/4), interpolation=2): 이미지를 랜덤한 크기 및 비율로 자른다.
- 참고: transforms.RandomSizedCrop는 RandomResizedCrop에 의해 deprecated되었다.
- transforms.RandomRotation(degrees, resample=False, expand=False, center=None): 이미지를 랜덤한 각도로 회전시킨다.
- transforms.ColorJitter(brightness=0, contrast=0, saturation=0, hue=0): brightness, contrast 등을 변화시킨다.
- 이미지를 torch.Tensor 또는 PILImage로 변환시킬 수 있다. 사용자 정의 변환도 가능하다.
- transforms.ToPILImage(mode=None): PILImage로 변환시킨다.
- transforms.ToTensor(): torch.Tensor로 변환시킨다.
- transforms.Lambda(lambd): 사용자 정의 lambda function을 적용시킨다.
- torch.Tensor에 적용해야 하는 변환 함수들도 있다.
- transforms.LinearTransformation(transformation_matrix): tensor로 표현된 이미지에 선형 변환을 시킨다.
- transforms.Normalize(mean, std, inplace=False): tensor의 데이터 수치(또는 범위)를 정규화한다.
- brightness나 contrast 등을 바꿀 수도 있다.
- transforms.functional.adjust_contrast(img, contrast_factor) 등
-
위의 변환 함수들을 랜덤으로 적용할지 말지 결정할 수도 있다.
- transforms.RandomChoice(transforms):
transforms리스트에 포함된 변환 함수 중 랜덤으로 1개 적용한다. - transforms.RandomApply(transforms, p=0.5):
transforms리스트에 포함된 변환 함수들을 p의 확률로 적용한다.
- transforms.RandomChoice(transforms):
-
위의 모든 변환 함수들을 하나로 조합하는 함수는 다음과 같다. 이 함수를
dataloader에 넘기면 이미지 변환 작업이 간단하게 완료된다.- transforms.Compose(transforms)
transforms.Compose([ transforms.CenterCrop(14), transforms.ToTensor(), transforms.Normalize(mean=(0.5, 0.5, 0.5), std=(0.5, 0.5, 0.5)) ])
- transforms.Compose(transforms)
변환 순서는 보통 resize/crop, toTensor, Normalize 순서를 거친다. Normalize는 tensor에만 사용 가능하므로 이 부분은 순서를 지켜야 한다.
torchtext
자연어처리(NLP)를 다룰 때 쓸 수 있는 좋은 라이브러리가 있다. 이는 자연어처리 데이터셋을 다루는 데 있어서 매우 편리한 기능을 제공한다.
- 데이터셋 로드
- 토큰화(Tokenization)
- 단어장(Vocabulary) 생성
- Index mapping: 각 단어를 해당하는 인덱스로 매핑
- 단어 벡터(Word Vector): word embedding을 만들어준다. 0이나 랜덤 값 및 사전학습된 값으로 초기화할 수 있다.
- Batch 생성 및 (자동) padding 수행
설치는 다음과 같다.
pip install torchtext
# conda 환경에선 다음과 같다.
conda install -c pytorch torchtext
Define and Load Model
Pytorch Model
gradient 계산 방식 등 Pytorch model의 작동 방식은 Set Loss function(creterion) and Optimizer 절을 보면 된다.
Pytorch에서 쓰는 용어는 Module 하나에 가깝지만, 많은 경우 layer나 model 등의 용어도 같이 사용되므로 굳이 구분하여 적어 보았다.
Layer : Model 또는 Module을 구성하는 한 개의 층, Convolutional Layer, Linear Layer 등이 있다.
Module : 1개 이상의 Layer가 모여서 구성된 것. Module이 모여 새로운 Module을 만들 수도 있다.
Model : 여러분이 최종적으로 원하는 것. 당연히 한 개의 Module일 수도 있다.
예를 들어 nn.Linear는 한 개의 layer이기도 하며, 이것 하나만으로도 module이나 Model을 구성할 수 있다. 단순 Linear Model이 필요하다면, model = nn.Linear(1, 1, True)처럼 사용해도 무방하다.
PyTorch의 모든 모델은 기본적으로 다음 구조를 갖는다. PyTorch 내장 모델뿐 아니라 사용자 정의 모델도 반드시 이 정의를 따라야 한다.
import torch.nn as nn
import torch.nn.functional as F
class Model_Name(nn.Module):
def __init__(self):
super(Model_Name, self).__init__()
self.module1 = ...
self.module2 = ...
"""
ex)
self.conv1 = nn.Conv2d(1, 20, 5)
self.conv2 = nn.Conv2d(20, 20, 5)
"""
def forward(self, x):
x = some_function1(x)
x = some_function2(x)
"""
ex)
x = F.relu(self.conv1(x))
x = F.relu(self.conv2(x))
"""
return x
PyTorch 모델로 쓰기 위해서는 다음 조건을 따라야 한다. 내장된 모델들(nn.Linear 등)은 당연히 이 조건들을 만족한다.
- torch.nn.Module을 상속해야 한다.
__init__()과forward()를 override해야 한다.- 사용자 정의 모델의 경우 init과 forward의 인자는 자유롭게 바꿀 수 있다. 이름이 x일 필요도 없으며, 인자의 개수 또한 달라질 수 있다.
이 두 가지 조건은 PyTorch의 기능들을 이용하기 위해 필수적이다.
따르지 않는다고 해서 에러를 내뱉진 않지만, 다음 규칙들은 따르는 것이 좋다:
__init__()에서는 모델에서 사용될 module을 정의한다. module만 정의할 수도, activation function 등을 전부 정의할 수도 있다.- 아래에서 설명하겠지만 module은 nn.Linear, nn.Conv2d 등을 포함한다.
- activation function은 nn.functional.relu, nn.functional.sigmoid 등을 포함한다.
forward()에서는 모델에서 행해져야 하는 계산을 정의한다(대개 train할 때). 모델에서 forward 계산과 backward gradient 계산이 있는데, 그 중 forward 부분을 정의한다. input을 네트워크에 통과시켜 어떤 output이 나오는지를 정의한다고 보면 된다.__init__()에서 정의한 module들을 그대로 갖다 쓴다.- 위의 예시에서는
__init__()에서 정의한self.conv1과self.conv2를 가져다 썼고, activation은 미리 정의한 것을 쓰지 않고 즉석에서 불러와 사용했다. - backward 계산은 PyTorch가 알아서 해 준다.
backward()함수를 호출하기만 한다면.
nn.Module
여기를 참고한다. 요약하면 nn.Module은 모든 PyTorch 모델의 base class이다.
nn.Module 내장 함수
nn.Module에 내장된 method들은 모델을 추가 구성/설정하거나, train/eval(test) 모드 변경, cpu/gpu 변경, 포함된 module 목록을 얻는 등의 활동에 초점이 맞춰져 있다.
모델을 추가로 구성하려면,
add_module(name, module): 현재 module에 새로운 module을 추가한다.apply(fn): 현재 module의 모든 submodule에 해당 함수(fn)을 적용한다. 주로 model parameter를 초기화할 때 자주 쓴다.
모델이 어떻게 생겼는지 보려면,
children(),modules(): 자식 또는 모델 전체의 모든 module에 대한 iterator를 반환한다.named_buffers(), named_children(), named_modules(), named_parameters(): 위 함수와 비슷하지만 이름도 같이 반환한다.
모델을 통째로 저장 혹은 불러오려면,
state_dict(destination=None, prefix='', keep_vars=False): 모델의 모든 상태(parameter, running averages 등 buffer)를 딕셔너리 형태로 반환한다.load_state_dict(state_dict, strict=True): parameter와 buffer 등 모델의 상태를 현 모델로 복사한다.strict=True이면 모든 module의 이름이 정확히 같아야 한다.
학습 시에 필요한 함수들을 살펴보면,
cuda(device=None): 모든 model parameter를 GPU 버퍼에 옮기는 것으로 GPU를 쓰고 싶다면 이를 활성화해주어야 한다.- GPU를 쓰려면 두 가지에 대해서만
.cuda()를 call하면 된다. 그 두 개는 모든 input batch 또는 tensor, 그리고 모델이다. .cuda()는 optimizer를 설정하기 전에 실행되어야 한다. 잊어버리지 않으려면 모델을 생성하자마자 쓰는 것이 좋다.
- GPU를 쓰려면 두 가지에 대해서만
eval(),train(): 모델을 train mode 또는 eval(test) mode로 변경한다. Dropout이나 BatchNormalization을 쓰는 모델은 학습시킬 때와 평가할 때 구조/역할이 다르기 때문에 반드시 이를 명시하도록 한다.parameters(recurse=True): module parameter에 대한 iterator를 반환한다. 보통 optimizer에 넘겨줄 때 말고는 쓰지 않는다.zero_grad(): 모든 model parameter의 gradient를 0으로 설정한다.
사용하는 법은 매우 간단히 나타내었다. Optimizer에 대한 설명은 여기를 참조하면 된다.
import torchvision
from torch import nn
def user_defined_initialize_function(m):
pass
model = torchvision.models.vgg16(pretrained=True)
# 예시는 예시일 뿐
last_module = nn.Linear(1000, 32, bias=True)
model.add_module('last_module', last_module)
last_module.apply(user_defined_initialize_function)
model.cuda()
# set optimizer. model.parameter를 넘겨준다.
optimizer = optim.Adam(model.parameters(), lr=0.0001, betas=(0.5, 0.999))
# train
model.train()
for idx, (data, label) in dataloader['train']:
...
# test
model.eval()
for idx, (data, label) in dataloader['test']:
...
Pytorch Layer의 종류
참조: nn.module
참고만 하도록 한다. 좀 많다. 쓰고자 하는 것과 이름이 비슷하다 싶으면 홈페이지를 참조해서 쓰면 된다.
- Linear layers
- nn.Linear
- nn.Bilinear
- Convolution layers
- nn.Conv1d, nn.Conv2d, nn.Conv3d
- nn.ConvTranspose1d, nn.ConvTranspose2d, nn.ConvTranspose3d
- nn.Unfold, nn.Fold
- Pooling layers
- nn.MaxPool1d, nn.MaxPool2d, nn.MaxPool3d
- nn.MaxUnpool1d, nn.MaxUnpool2d, nn.MaxUnpool3d
- nn.AvgPool1d, nn.AvgPool2d, nn.AvgPool3d
- nn.FractionalMaxPool2d
- nn.LPPool1d, nn.LPPool2d
- nn.AdaptiveMaxPool1d, nn.AdaptiveMaxPool2d, nn.AdaptiveMaxPool3d
- nn.AdaptiveAvgPool1d, nn.AdaptiveAvgPool2d, nn.AdaptiveAvgPool3d
- Padding layers
- nn.ReflectionPad1d, nn.ReflectionPad2d
- nn.ReplicationPad1d, nn.ReplicationPad2d, nn.ReplicationPad3d
- nn.ZeroPad2d
- nn.ConstantPad1d, nn.ConstantPad2d, nn.ConstantPad3d
- Normalization layers
- nn.BatchNorm1d, nn.BatchNorm2d, nn.BatchNorm3d
- nn.GroupNorm
- nn.InstanceNorm1d, nn.InstanceNorm2d, nn.InstanceNorm3d
- nn.LayerNorm
- nn.LocalResponseNorm
- Recurrent layers
- nn.RNN, nn.RNNCell
- nn.LSTM, nn.LSTMCell
- nn.GRU, nn.GRUCell
- Dropout layers
- nn.Dropout, nn.Dropout2d, nn.Dropout3d
- nn.AlphaDropout
- Sparse layers
- nn.Embedding
- nn.EmbeddingBag
Pytorch Activation function의 종류
- Non-linear activations
- nn.ELU, nn.SELU
- nn.Hardshrink, nn.Hardtanh
- nn.LeakyReLU, nn.PReLU, nn.ReLU, nn.ReLU6, nn.RReLU
- nn.Sigmoid, nn.LogSigmoid
- nn.Softplus, nn.Softshrink, nn.Softsign
- nn.Tanh, nn.Tanhshrink
- nn.Threshold
- Non-linear activations (other)
- nn.Softmin
- nn.Softmax, nn.Softmax2d, nn.LogSoftmax
- nn.AdaptiveLogSoftmaxWithLoss
Containers
참조: Containers
여러 layer들을 하나로 묶는 데 쓰인다.
종류는 다음과 같은 것들이 있는데, Module 설계 시 자주 쓰는 것으로 nn.Sequential이 있다.
- nn.Module
- nn.Sequential
- nn.ModuleList
- nn.ModuleDict
- nn.ParameterList
- nn.ParameterDict
nn.Sequential
참조: nn.Sequential
이름에서 알 수 있듯 여러 module들을 연속적으로 연결하는 모델이다.
# Example of using Sequential
model = nn.Sequential(
nn.Conv2d(1,20,5),
nn.ReLU(),
nn.Conv2d(20,64,5),
nn.ReLU()
)
"""
이 경우 model(x)는 nn.ReLU(nn.Conv2d(20,64,5)(nn.ReLU(nn.Conv2d(1,20,5)(x))))와 같음.
"""
# Example of using Sequential with OrderedDict
model = nn.Sequential(OrderedDict([
('conv1', nn.Conv2d(1,20,5)),
('relu1', nn.ReLU()),
('conv2', nn.Conv2d(20,64,5)),
('relu2', nn.ReLU())
]))
조금 다르지만 비슷한 역할을 할 수 있는 것으로는 nn.ModuleList, nn.ModuleDict가 있다.
모델 구성 방법
크게 6가지 정도의 방법이 있다. nn 라이브러리를 잘 써서 직접 만들거나, 함수 또는 클래스로 정의, cfg파일 정의 또는 torchvision.models에 미리 정의된 모델을 쓰는 방법이 있다.
단순한 방법
model = nn.Linear(in_features=1, out_features=1, bias=True)
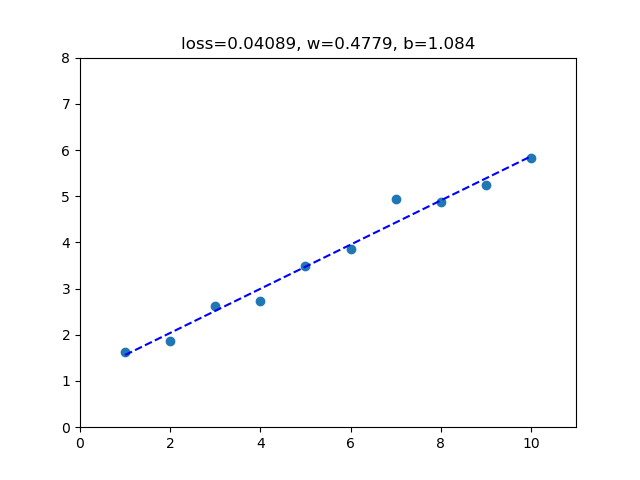
이전 글에서 썼던 방식이다. 매우 단순한 모델을 만들 때는 굳이 nn.Module을 상속하는 클래스를 만들 필요 없이 바로 사용 가능하며, 단순하다는 장점이 있다.
nn.Sequential을 사용하는 방법
sequential_model = nn.Sequential(
nn.Linear(in_features=1, out_features=20, bias=True),
nn.ReLU(),
nn.Linear(in_features=20, out_features=1, bias=True),
)
여러 Layer와 Activation function들을 조합하여 하나의 sequential model을 만들 수 있다. 역시 상대적으로 복잡하지 않은 모델 중 모델의 구조가 sequential한 모델에만 사용할 수 있다.
함수로 정의하는 방법
def TwoLayerNet(in_features=1, hidden_features=20, out_features=1):
hidden = nn.Linear(in_features=in_features, out_features=hidden_features, bias=True)
activation = nn.ReLU()
output = nn.Linear(in_features=hidden_features, out_features=out_features, bias=True)
net = nn.Sequential(hidden, activation, output)
return net
model = TwoLayerNet(1, 20, 1)
바로 위의 모델과 완전히 동일한 모델이다. 함수로 선언할 경우 변수에 저장해 놓은 layer들을 재사용하거나, skip-connection을 구현할 수도 있다. 하지만 그 정도로 복잡한 모델은 아래 방법을 쓰는 것이 낫다.
nn.Module을 상속한 클래스를 정의하는 방법
가장 정석이 되는 방법이다. 또한, 복잡한 모델을 구현하는 데 적합하다.
from torch import nn
import torch.nn.functional as F
class TwoLinearLayerNet(nn.Module):
def __init__(self, in_features, hidden_features, out_features):
super(TwoLinearLayerNet, self).__init__()
self.linear1 = nn.Linear(in_features=in_features, out_features=hidden_features, bias=True)
self.linear2 = nn.Linear(in_features=hidden_features, out_features=out_features, bias=True)
def forward(self, x):
x = F.relu(self.linear1(x))
return self.linear2(x)
model = TwoLinearLayerNet(1, 20, 1)
역시 동일한 모델을 구현하였다. 여러분의 코딩 스타일에 따라, ReLU 등의 Activation function을 forward()에서 바로 정의해서 쓰거나, __init__()에 정의한 후 forward에서 갖다 쓰는 방법을 선택할 수 있다. 후자의 방법은 아래와 같다.
물론 변수명은 전적으로 여러분의 선택이지만, activation1, relu1 등의 이름을 보통 쓰는 것 같다.
from torch import nn
class TwoLinearLayerNet(nn.Module):
def __init__(self, in_features, hidden_features, out_features):
super(TwoLinearLayerNet, self).__init__()
self.linear1 = nn.Linear(in_features=in_features, out_features=hidden_features, bias=True)
self.activation1 = nn.ReLU()
self.linear2 = nn.Linear(in_features=hidden_features, out_features=out_features, bias=True)
def forward(self, x):
x = self.activation1(self.linear1(x))
return self.linear2(x)
model = TwoLinearLayerNet(1, 20, 1)
두 코딩 스타일의 차이점 중 하나는 import하는 것이 다르다(F.relu와 nn.ReLU는 사실 거의 같다). Activation function 부분에서 torch.nn.functional은 torch.nn의 Module에 거의 포함되는데, forward()에서 정의해서 쓰느냐 마느냐에 따라 다르게 선택하면 되는 정도이다.
cfg(config)를 정의한 후 모델을 생성하는 방법
처음 보면 알아보기 까다로운 방법이지만, 매우 복잡한 모델의 경우 .cfg 파일을 따로 만들어 모델의 구조를 정의하는 방법이 존재한다. 많이 쓰이는 방법은 대략 두 가지 정도인 것 같다.
먼저 PyTorch documentation에서 찾을 수 있는 방법이 있다. 예로는 VGG를 가져왔다. 코드는 여기에서 찾을 수 있다.
class VGG(nn.Module):
def __init__(self, features, num_classes=1000, init_weights=True):
super(VGG, self).__init__()
self.features = features
self.classifier = nn.Sequential(...)
if init_weights:
self._initialize_weights()
def forward(self, x):...
def _initialize_weights(self):...
def make_layers(cfg, batch_norm=False):
layers = []
in_channels = 3
for v in cfg:
if v == 'M':
layers += [nn.MaxPool2d(kernel_size=2, stride=2)]
else:
conv2d = nn.Conv2d(in_channels, v, kernel_size=3, padding=1)
if batch_norm:
layers += [conv2d, nn.BatchNorm2d(v), nn.ReLU(inplace=True)]
else:
layers += [conv2d, nn.ReLU(inplace=True)]
in_channels = v
return nn.Sequential(*layers)
cfg = {
'A': [64, 'M', 128, 'M', 256, 256, 'M', 512, 512, 'M', 512, 512, 'M'],
'B': [64, 64, 'M', 128, 128, 'M', 256, 256, 'M', 512, 512, 'M', 512, 512, 'M'],
'D': [64, 64, 'M', 128, 128, 'M', 256, 256, 256, 'M', 512, 512, 512, 'M', 512, 512, 512, 'M'],
'E': [64, 64, 'M', 128, 128, 'M', 256, 256, 256, 256, 'M', 512, 512, 512, 512, 'M', 512, 512, 512, 512, 'M'],
}
def vgg16(pretrained=False, **kwargs):
"""VGG 16-layer model (configuration "D")"""
if pretrained:
kwargs['init_weights'] = False
model = VGG(make_layers(cfg['D']), **kwargs)
if pretrained:
model.load_state_dict(model_zoo.load_url(model_urls['vgg16']))
return model
여기서는 .cfg 파일이 사용되지는 않았으나, cfg라는 변수가 configuration을 담당하고 있다. VGG16 모델을 구성하기 위해 cfg 변수의 해당하는 부분을 읽어 make_layer 함수를 통해 모델을 구성한다.
더 복잡한 모델은 아예 따로 .cfg 파일을 빼놓는다. YOLO의 경우 수백 라인이 넘기도 한다.
.cfg 파일은 대략 다음과 같이 생겼다.
[net]
# Testing
batch=1
subdivisions=1
# Training
# batch=64
# subdivisions=8
...
[convolutional]
batch_normalize=1
filters=32
size=3
stride=1
pad=1
activation=leaky
[maxpool]
size=2
stride=2
...
이를 파싱하는 코드도 있어야 한다.
def parse_cfg(cfgfile):
blocks = []
fp = open(cfgfile, 'r')
block = None
line = fp.readline()
while line != '':
line = line.rstrip()
if line == '' or line[0] == '#':
line = fp.readline()
continue
elif line[0] == '[':
if block:
blocks.append(block)
block = dict()
block['type'] = line.lstrip('[').rstrip(']')
# set default value
if block['type'] == 'convolutional':
block['batch_normalize'] = 0
else:
key,value = line.split('=')
key = key.strip()
if key == 'type':
key = '_type'
value = value.strip()
block[key] = value
line = fp.readline()
if block:
blocks.append(block)
fp.close()
return blocks
이 방법의 경우 대개 depth가 수십~수백에 이르는 아주 거대한 모델을 구성할 때 사용되는 방법이다. 많은 수의 github 코드들이 이런 방식을 사용하고 있는데, 그러면 그 모델은 굉장히 복잡하게 생겼다는 뜻이 된다.
torchvision.models의 모델을 사용하는 방법
torchvision.models에서는 미리 정의되어 있는 모델들을 사용할 수 있다. 이 모델들은 그 구조뿐 아니라 pretrained=True 인자를 넘김으로써 pretrained weights를 가져올 수도 있다.
2019.02.12 시점에서 사용 가능한 모델 종류는 다음과 같다.
- AlexNet
- VGG-11, VGG-13, VGG-16, VGG-19
- VGG-11, VGG-13, VGG-16, VGG-19 (with batch normalization)
- ResNet-18, ResNet-34, ResNet-50, ResNet-101, ResNet-152
- SqueezeNet 1.0, SqueezeNet 1.1
- Densenet-121, Densenet-169, Densenet-201, Densenet-161
- Inception v3
모델에 따라 train mode와 eval mode가 정해진 경우가 있으므로 이는 주의해서 사용하도록 한다.
모든 pretrained model을 쓸 때 이미지 데이터는 [3, W, H] 형식이어야 하고, W, H는 224 이상이어야 한다. 또 아래 코드처럼 정규화된 이미지 데이터로 학습된 것이기 때문에, 이 모델들을 사용할 때에는 데이터셋을 이와 같이 정규화시켜주어야 한다.
transforms.Normalize(mean=[0.485, 0.456, 0.406],
std=[0.229, 0.224, 0.225])
사용법은 대략 다음과 같다. 사실 이게 거의 끝이고, 나머지는 다른 일반 모델처럼 사용하면 된다.
import torchvision.models as models
# model load
alexnet = models.alexnet()
vgg16 = models.vgg16()
vgg16_bn = models.vgg16_bn()
resnet18 = models.resnet18()
squeezenet = models.squeezenet1_0()
densenet = models.densenet161()
inception = models.inception_v3()
# pretrained model load
resnet18 = models.resnet18(pretrained=True)
vgg16 = models.vgg16(pretrained=True)
...
Set Loss function(creterion) and Optimizer
Pytorch Loss function의 종류
참조: Loss functions
Loss function은 모델이 추측한 결과(prediction 또는 output)과 실제 정답(label 또는 y 등)의 loss를 계산한다. 이는 loss function을 어떤 것을 쓰느냐에 따라 달라진다. 예를 들어 regression model에서 MSE(Mean Squared Error)를 쓸 경우 평균 제곱오차를 계산한다.
사용법은 다른 함수들도 아래와 똑같다.
import torch
from torch import nn
criterion = nn.MSELoss()
prediction = torch.Tensor([12, 21, 30, 41, 52]) # 예측값
target = torch.Tensor([10, 20, 30, 40, 50]) # 정답
loss = criterion(prediction, target)
print(loss)
# tensor(2.)
# loss = (2^2 + 1^2 + 0^2 + 1^2 + 2^2) / 5 = 2
criterion_reduction_none = nn.MSELoss(reduction='none')
loss = criterion_reduction_none(prediction, target)
print(loss)
# tensor([4., 1., 0., 1., 4.])
여러 코드들을 살펴보면, loss function을 정의할 때는 보통 creterion, loss_fn, loss_function등의 이름을 사용하니 참고하자.
홈페이지를 참조하면 각 함수별 설명에 ‘Creates a criterion that measures…‘라 설명이 되어 있다. 위의 예시를 보면 알겠지만 해당 함수들이 당장 loss를 계산하는 것이 아니라 loss를 계산하는 기준을 정의한다는 뜻이다.
또 많은 함수들은 reduce와 size_average argument를 갖는다. loss를 계산하여 평균을 내는 것이 아니라 각 원소별로 따로 계산할 수 있게 해 준다. 그러나 2019.02.16 기준으로 다음과 비슷한 경고가 뜬다.
reduce args will be deprecated, please use reduction=’none’ instead.
따라서 reduction argument를 쓰도록 하자. 지정할 수 있는 종류는 ‘none’ | ‘mean’ | ‘sum’ 세 가지이다. 기본값은 mean으로 되어 있다.
- nn.L1Loss: 각 원소별 차이의 절댓값을 계산한다.
- nn.MSELoss: Mean Squared Error(평균제곱오차) 또는 squared L2 norm을 계산한다.
- nn.CrossEntropyLoss: Cross Entropy Loss를 계산한다. nn.LogSoftmax() and nn.NLLLoss()를 포함한다. weight argument를 지정할 수 있다.
- nn.CTCLoss: Connectionist Temporal Classification loss를 계산한다.
- nn.NLLLoss: Negative log likelihood loss를 계산한다.
- nn.PoissonNLLLoss: target이 poission 분포를 가진 경우 Negative log likelihood loss를 계산한다.
- nn.KLDivLoss: Kullback-Leibler divergence Loss를 계산한다.
- nn.BCELoss: Binary Cross Entropy를 계산한다.
- nn.BCEWithLogitsLoss: Sigmoid 레이어와 BCELoss를 하나로 합친 것인데, 홈페이지의 설명에 따르면 두 개를 따로 쓰는 것보다 이 함수를 쓰는 것이 조금 더 수치 안정성을 가진다고 한다.
- 이외에 MarginRankingLoss, HingeEmbeddingLoss, MultiLabelMarginLoss, SmoothL1Loss, SoftMarginLoss, MultiLabelSoftMarginLoss, CosineEmbeddingLoss, MultiMarginLoss, TripletMarginLoss를 계산하는 함수들이 있다. 필요하면 찾아보자.
Pytorch Optimizer의 종류
참조: torch.optim
여기에도 간략하게 언급했었지만, GPU CUDA를 사용할 계획이라면 optimizer를 정의하기 전에 미리 해놓아야 한다(model.cuda()). 공식 홈페이지에 따르면,
If you need to move a model to GPU via .cuda(), please do so before constructing optimizers for it. Parameters of a model after .cuda() will be different objects with those before the call. In general, you should make sure that optimized parameters live in consistent locations when optimizers are constructed and used.
이유를 설명하자면
- optimizer는 argument로 model의 parameter를 입력받는다.
.cuda()를 쓰면 모델의 parameter가 cpu 대신 gpu에 올라가는 것이므로 다른 object가 된다.- 따라서 optimizer에 model parameter의 위치를 전달한 후
.cuda()를 실행하면, 학습시켜야 할 parameter는 GPU에 올라가 있는데 optimizer는 cpu에 올라간 엉뚱한 parameter 위치를 참조하고 있는 것이 된다.
그러니 순서를 지키자.
optimizer 정의는 다음과 같이 할 수 있다.
optimizer = optim.SGD(model.parameters(), lr = 0.01, momentum=0.9)
optimizer = optim.Adam([var1, var2], lr = 0.0001)
optimizer에 대해 알아 두어야 할 것이 조금 있다.
- optimizer는
step()method를 통해 argument로 전달받은 parameter를 업데이트한다. - 모델의 parameter별로(per-parameter) 다른 기준(learning rate 등)을 적용시킬 수 있다. 참고
torch.optim.Optimizer(params, defaults)는 모든 optimizer의 base class이다.nn.Module과 같이state_dict()와load_state_dict()를 지원하여 optimizer의 상태를 저장하고 불러올 수 있다.zero_grad()method는 optimizer에 연결된 parameter들의 gradient를 0으로 만든다.torch.optim.lr_scheduler는 epoch에 따라 learning rate를 조절할 수 있다.
Optimizer의 종류:
- optim.Adadelta, optim.Adagrad, optim.Adam, optim.SparseAdam, optim.Adamax
- optim.ASGD, optim.LBFGS
- optim.RMSprop, optim.Rprop
- optim.SGD
LBFGS는 per-parameter 옵션이 지원되지 않는다. 또한 memory를 다른 optimizer에 비해 많이 잡아먹는다고 한다.
Pytorch LR(Learning Rate) Scheduler의 종류
LR(Learning Rate) Scheduler는 미리 지정한 횟수의 epoch이 지날 때마다 lr을 감소(decay)시켜준다.
이는 학습 초기에는 빠르게 학습을 진행시키다가 minimum 근처에 다다른 것 같으면 lr을 줄여서 더 최적점을 잘 찾아갈 수 있게 해주는 것이다.
종류는 여러 개가 있는데, 마음에 드는 것을 선택하면 된다. 아래쪽에 어떻게 lr이 변화하는지 그림을 그려 놓았다.
lr Scheduler의 종류:
- optim.lr_scheduler.LambdaLR: lambda 함수를 하나 받아 그 함수의 결과를 lr로 설정한다.
- optim.lr_scheduler.StepLR: 특정 step마다 lr을 gamma 비율만큼 감소시킨다.
- optim.lr_scheduler.MultiStepLR: StepLR과 비슷한데 매 step마다가 아닌 지정된 epoch에만 gamma 비율로 감소시킨다.
- optim.lr_scheduler.ExponentialLR: lr을 지수함수적으로 감소시킨다.
- optim.lr_scheduler.CosineAnnealingLR: lr을 cosine 함수의 형태처럼 변화시킨다. lr이 커졌다가 작아졌다가 한다.
- optim.lr_scheduler.ReduceLROnPlateau: 이 scheduler는 다른 것들과는 달리 학습이 잘 되고 있는지 아닌지에 따라 동적으로 lr을 변화시킬 수 있다. 보통 validation set의 loss를 인자로 주어서 사전에 지정한 epoch동안 loss가 줄어들지 않으면 lr을 감소시키는 방식이다.
각 scheduler는 공통적으로 last_epoch argument를 갖는다. Default value로 -1을 가지며, 이는 초기 lr을 optimizer에서 지정된 lr로 설정할 수 있도록 한다.
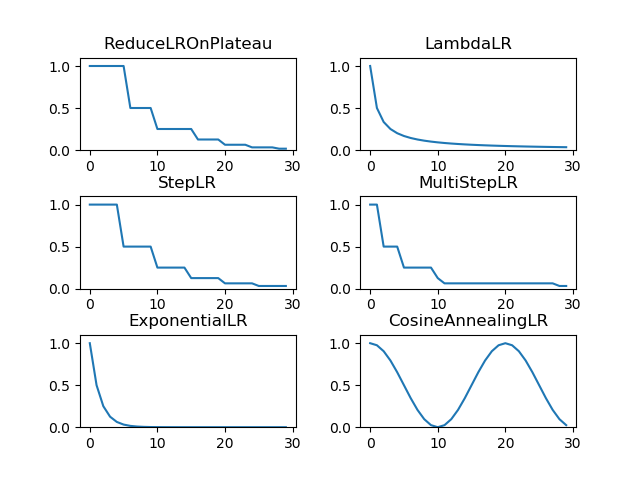
코드는 아래와 같이 작성하였다.
from torch import optim
from torch import nn
import re
import random
from matplotlib import pyplot as plt
class Model(nn.Module):
def __init__(self):
super(Model, self).__init__()
self.linear1 = nn.Linear(5, 3)
def forward(self, x):
return self.linear1(x)
model = Model()
optimizer = optim.Adam(model.parameters(), lr=1.0)
scheduler_list = [
optim.lr_scheduler.ReduceLROnPlateau(optimizer=optimizer,
mode='min',
factor=0.5,
patience=3, ), # 이외에도 인자가 많다. 찾아보자.
optim.lr_scheduler.LambdaLR(optimizer=optimizer,
lr_lambda=lambda epoch: 1 / (epoch+1)),
optim.lr_scheduler.StepLR(optimizer=optimizer,
step_size=5,
gamma=0.5),
optim.lr_scheduler.MultiStepLR(optimizer=optimizer,
milestones=[2, 5, 10, 11, 28],
gamma=0.5),
optim.lr_scheduler.ExponentialLR(optimizer=optimizer,
gamma=0.5),
optim.lr_scheduler.CosineAnnealingLR(optimizer=optimizer,
T_max=10,
eta_min=0),
]
reObj = re.compile(r'<torch\.optim\.lr_scheduler\.(.+) object.*>')
for i, scheduler in enumerate(scheduler_list):
scheduler_name = reObj.match(str(scheduler)).group(1)
print(scheduler_name)
lr_list = []
for epoch in range(1, 30+1):
if str(scheduler_name) == 'ReduceLROnPlateau':
scheduler.step(random.randint(1, 50))
else:
scheduler.step()
lr = optimizer.param_groups[0]['lr']
# print('epoch: {:3d}, lr={:.6f}'.format(epoch, lr))
lr_list.append(lr)
plt.subplot(3, 2, i + 1)
plt.title(scheduler_name)
plt.ylim(0, 1.1)
plt.plot(lr_list)
plt.show()
# plt.savefig('scheduler')
조금 더 자세한 설명은 홈페이지를 참조하자.
from torch import optim
from torch import nn
class Model(nn.Module):
def __init__(self):
super(Model, self).__init__()
self.linear1 = nn.Linear(5, 3)
def forward(self, x):
return self.linear1(x)
model = Model()
optimizer = optim.Adam(model.parameters(), lr=1.0) # 1.0은 보통 너무 크다. 하지만 예시이므로 1을 주었다.
# Learning Rate가 scheduler에 따라 어떻게 변하는지 보려면 이곳을 바꾸면 된다.
scheduler = optim.lr_scheduler.LambdaLR(optimizer=optimizer,
lr_lambda=lambda epoch: 0.95 ** epoch)
for epoch in range(1, 100+1):
for param_group in optimizer.param_groups:
lr = param_group['lr']
print('epoch: {:3d}, lr={:.6f}'.format(epoch, lr))
scheduler.step()
결과:
epoch: 1, lr=1.000000
epoch: 2, lr=1.000000
epoch: 3, lr=0.950000
epoch: 4, lr=0.902500
epoch: 5, lr=0.857375
epoch: 6, lr=0.814506
epoch: 7, lr=0.773781
epoch: 8, lr=0.735092
epoch: 9, lr=0.698337
epoch: 10, lr=0.663420
...
Train Model
일반적인 machine learning의 학습 방법은 다음과 같다. 입력은 input, 모델의 출력은 output, 정답은 target이라고 하자.
- model structure, loss function, optimizer 등을 정한다.
- forward-propagation: input을 모델에 통과시켜 output을 계산한다.
- loss function으로 output과 target 간 loss를 계산한다.
- back-propagation: loss와 chain rule을 활용하여 모델의 각 레이어에서 gradient($\Delta w$)를 계산한다.
- update: $ w \leftarrow w - \alpha\Delta w $식에 의해 모델의 parameter를 update한다.
Pytorch의 학습 방법은 다음과 같다.
- model structure, loss function, optimizer 등을 정한다.
optimizer.zero_grad(): 이전 epoch에서 계산되어 있는 parameter의 gradient를 0으로 초기화한다.output = model(input): input을 모델에 통과시켜 output을 계산한다.loss = loss_fn(output, target): output과 target 간 loss를 계산한다.loss.backward(): loss와 chain rule을 활용하여 모델의 각 레이어에서 gradient($\Delta w$)를 계산한다.optimizer.step(): $w \leftarrow w - \alpha\Delta w$식에 의해 모델의 parameter를 update한다.
거의 일대일 대응되지만 다른 점이 하나 있다.
optimizer.zero_grad(): Pytorch는 gradient를loss.backward()를 통해 계산하지만, 이 함수는 이전 gradient를 덮어쓴 뒤 새로 계산하는 것이 아니라, 이전 gradient에 누적하여 계산한다.- 귀찮은데? 라고 생각할 수는 있다. 그러나 이러한 누적 계산 방식은 RNN 모델을 구현할 때는 오히려 훨씬 편하게 코드를 작성할 수 있도록 도와준다.
- 그러니 gradient가 누적될 필요 없는 모델에서는 model에 input를 통과시키기 전
optimizer.zero_grad()를 한번 호출해 주기만 하면 된다고 생각하면 끝이다.
Pytorch가 대체 어떻게 loss.backward() 단 한번에 gradient를 자동 계산하는지에 대한 설명도 하면,
- 모든 Pytorch Tensor는
requires_gradargument를 가진다. 일반적으로 생성하는 Tensor는 기본적으로 해당 argument 값이False이며, 따로True로 설정해 주면 gradient를 계산해 주어야 한다.nn.Linear등의 module은 생성할 때 기본적으로requires_grad=True이기 때문에, 일반적으로 모델의 parameter는 gradient를 계산하게 된다.- 참고(3번 항목): Pytorch 0.4.0 버전 이전에는
Variableclass가 해당 역할을 수행하였지만, deprecated되었다.
- 참고(3번 항목): Pytorch 0.4.0 버전 이전에는
- 마지막 레이어만 원하는 것으로 바꿔서 그 레이어만 학습을 수행하는 형태의 transfer learning을
requires_grad를 이용해 손쉽게 구현할 수 있다. 이외에도 특정 레이어만 gradient를 계산하지 않게 하는 데에도 쓸 수 있다. 아래 예시는 512개의 class 대신 100개의 class를 구별하고자 할 때 resnet18을 기반으로 transfer learning을 수행하는 방식이다.
model = torchvision.models.resnet18(pretrained=True)
for param in model.parameters():
param.requires_grad = False
# Replace the last fully-connected layer
# Parameters of newly constructed modules have requires_grad=True by default
model.fc = nn.Linear(512, 100)
# Optimize only the classifier
optimizer = optim.SGD(model.fc.parameters(), lr=1e-2, momentum=0.9)
requires_grad=True인 Tensor로부터 연산을 통해 생성된 Tensor도requires_grad=True이다.with torch.no_grad():범위 안에서는 gradient 계산을 하지 않는다.with torch.no_grad():안에서 선언된with torch.enable_grad():범위 안에서는 다시 gradient 계산을 한다. 이 두 가지 기능을 통해 국지적으로 gradient 계산을 수행하거나 수행하지 않을 수 있다.
import torch
x = torch.Tensor(1)
print('x.requires_grad:', x.requires_grad)
y = torch.ones(1, requires_grad=True)
print('y.requires_grad:', y.requires_grad)
z = 172 * y + 3
print('z.requires_grad:', z.requires_grad)
with torch.no_grad():
print('z.requires_grad:', (z ** 2).requires_grad)
with torch.enable_grad():
print('z.requires_grad:', (z ** 2).requires_grad)
print('z.grad_fn:', z.grad_fn)
print('x:', x, '\ny:', y, '\nz:', z)
z.backward()
print('y.grad:', y.grad)
print('z.grad:', z.grad)
x.requires_grad: False
y.requires_grad: True
z.requires_grad: True
z.requires_grad: False
z.requires_grad: True
z.grad_fn: <AddBackward0 object at 0x0000028634614780>
x: tensor([1.4013e-45])
y: tensor([1.], requires_grad=True)
z: tensor([175.], grad_fn=<AddBackward0>)
y.grad: tensor([172.])
z.grad: None
튜토리얼이 조금 더 궁금하다면 여기를 참고해도 좋다.
학습할 때 알아두면 괜찮은 것들을 대략 정리해보았다. 어떤 식으로 학습하는 것이 좋은지(learning rate 선택 기준 등)는 양이 너무 방대하기에 여기에는 적지 않는다.
CUDA: use GPU
torch.cuda.is_available(): 학습을 시킬 때는 GPU를 많이 사용한다. GPU가 사용가능한지 알 수 있다.torch.cuda.device(device): 어느 device(GPU나 CPU)를 쓸 지 선택한다.torch.cuda.device_count(): 현재 선택된 device의 수를 반환한다.torch.cuda.init(): C API를 쓰는 경우 명시적으로 호출해야 한다.torch.cuda.set_device(device): 현재 device를 설정한다.torch.cuda.manual_seed(seed): 랜덤 숫자를 생성할 시드를 정한다. multi-gpu 환경에서는manual_seed_all함수를 사용한다.torch.cuda.empty_cache(): 사용되지 않는 cache를 release하나, 가용 메모리를 늘려 주지는 않는다.
간단한 학습 과정은 다음 구조를 따른다.
# 변수명으로 input을 사용하는 것은 비추천. python 내장 함수 이름이다.
for data, target in dataloader:
optimizer.zero_grad() # RNN에서는 생략될 수 있음
output = model(data)
loss = loss_fn(output, target)
loss.backward()
optimizer.step()
Visualize and save results
Visualization Library
Visualization은 이 글에서 설명하지 않겠다. 기본적으로 python의 그래프 패키지인 matplotlib을 많이 쓰며, graphviz, seaborn 등의 다른 라이브러리도 잘 보이는 편이다.
Save & Load Model
모델을 저장하는 방법은 여러 가지가 있지만, pytorch를 사용할 때는 다음 방법이 가장 권장된다. 아주 유연하고 또 간단하기 때문이다.
Save:
torch.save(model.state_dict(), PATH)
Load:
model = TheModelClass(*args, **kwargs)
model.load_state_dict(torch.load(PATH))
# model.eval() # 테스트 시
# 참고로 model.load_state_dict(PATH)와 같이 쓸 수는 없다.
epoch별로 checkpoint를 쓰면서 저장할 때는 다음과 같이 혹은 비슷하게 쓰면 좋다. checkpoint를 쓸 때는 단순히 모델의 parameter뿐만 아니라 epoch, loss, optimizer 등을 저장할 필요가 있다.
Save:
torch.save({
'epoch': epoch,
'model_state_dict': model.state_dict(),
'optimizer_state_dict': optimizer.state_dict(),
'loss': loss,
...
}, PATH)
Load:
model = TheModelClass(*args, **kwargs)
optimizer = TheOptimizerClass(*args, **kwargs)
checkpoint = torch.load(PATH)
model.load_state_dict(checkpoint['model_state_dict'])
optimizer.load_state_dict(checkpoint['optimizer_state_dict'])
epoch = checkpoint['epoch']
loss = checkpoint['loss']
# model.train() or model.eval()
일반적으로 저장한 모델 파일명은 .pt나 .pth 확장자를 쓴다. 모델을 포함하여 여러 가지를 같이 저장할 때는 .tar 확장자를 자주 쓰는 편이다.
모델을 불러오고 나서 계속 학습시킬 것이라면 model.train(), 테스트를 할 것이라면 model.eval()으로 모드를 설정하도록 한다. 이유는 이 글에 설명이 있다.
모델이 여러 개라면
torch.save({
'modelA_state_dict': modelA.state_dict(),
'modelB_state_dict': modelB.state_dict(),
...
처럼 쓰면 그만이다.
구조가 조금 다른 모델에다가 parameter를 load하고 싶을 경우 load할 때 다음처럼 쓴다.
model.load_state_dict(torch.load(PATH), strict=False)
load_state_dict 함수는 기본적으로 strict=True 옵션을 갖고 있으며, 이는 불러올 모델과 저장된 모델의 레이어의 개수와 이름 등이 같아야만 오류 없이 불러온다.
따라서 transfer learning이나, 복잡한 모델을 새로 학습시키고 싶을 때 모델의 일부라도 parameter를 불러오고 싶다면 strict=False argument를 설정하면 된다.
이는 레이어들이 정확히 일치하지 않아도 매칭이 되는 레이어가 일부라도 있다면 그 레이어들에 한해서 parameter를 load한다.
또 parameter 개수는 같지만 이름은 다른 레이어에 parameter를 불러오고 싶을 때는, state_dict는 딕셔너리이기 때문에 그냥 해당 딕셔너리의 이름만 바꿔서 load하면 그만이다.
pickle 또는 torch.save를 통해 model 전체를 통째로 저장하는 방법은 간편하기는 하지만 이후 불러올 때는 해당 모델과 완전히 똑같이 생긴 모델에만 사용 가능하기 때문에 확장성과 재사용성이 떨어진다.
layer 이름과 parameter를 mapping하여 저장하는 state_dict를 쓰는 것이 transfer learinng을 쉽게 할 수 있는 등 범용성이 더 좋다.
device를 바꿔서 저장하고 싶다면, load_state_dict에서 map_location argument를 설정하거나, model.to(device) 함수를 사용하면 된다. 자세한 것은 홈페이지를 참조한다. GPU를 사용할 때 바꿔줘야 하는 부분은 여기의 cuda 부분을 참고한다.
torch.save & torch.load
내부적으로 pickle을 사용하며, 따라서 모델뿐 아니라 일반 tensor, 기타 다른 모든 python 객체를 저장할 수 있다.
nn.Module.state_dict & nn.Module.load_state_dict
우선 state_dict는 간단히 말해 모델의 상태를 딕셔너리 형태로 표현하는 것이다. 그러면 모델의 상태는 어떻게 정의되는가?
state_dict로 저장되는 모델의 상태는 learnable parameters이며, state_dict는 {레이어 이름: parameter tensor}의 형태를 갖는 딕셔너리이다.
딱 그뿐이다. 간단하지 않은가?
Optimizer도 state_dict를 갖고 있는데, 이 경우는 사용된 hyperparameter 등의 상태가 저장된다.
공식 홈페이지의 예시를 일부 가져오면 다음과 같다.
# 모델이 이렇게 생겼으면,
self.conv1 = nn.Conv2d(3, 6, 5)
self.pool = nn.MaxPool2d(2, 2)
self.conv2 = nn.Conv2d(6, 16, 5)
self.fc1 = nn.Linear(16 * 5 * 5, 120)
# 이 코드에 의해
for param_tensor in model.state_dict():
print(param_tensor, "\t", model.state_dict()[param_tensor].size())
# 이렇게 출력된다.
conv1.weight torch.Size([6, 3, 5, 5])
conv1.bias torch.Size([6])
conv2.weight torch.Size([16, 6, 5, 5])
conv2.bias torch.Size([16])
fc1.weight torch.Size([120, 400])
fc1.bias torch.Size([120])
# optimizer는
optimizer = optim.SGD(model.parameters(), lr=0.001, momentum=0.9)
for var_name in optimizer.state_dict():
print(var_name, "\t", optimizer.state_dict()[var_name])
# 이렇다.
state {}
param_groups [{'lr': 0.001, 'momentum': 0.9, 'dampening': 0, 'weight_decay': 0,
'nesterov': False, 'params': [4675713712, 4675713784, ..., 4675714720]}]
Q & A
model.train()과model.eval()은 모델이 학습 모드인지, 테스트 모드인지를 정하는 것이다. 이는 dropout이나 batchnorm이 있는 모델의 경우 학습할 때와 테스트할 때 모델이 달라지기 때문에 세팅하는 것이다(또한 필수이다).torch.no_grad()는 (대개 일시적으로) 해당 범위 안에서 gradient 계산을 중지시킴으로써 메모리 사용량을 줄이고 계산 속도를 빨리 하는 것이다. 참고optimizer.zero_grad()를 사용하는 이유. 참고- Pytorch 코드들 중에는
torch.autograd.Variable을 사용한 경우가 많다. Pytorch 0.4.0 버전 이후로는 Tensor 클래스에 통합되어 더 이상 쓸 필요가 없다. 참고(3번 항목) - 역시 Pytorch 코드들 중에는 loss를 tensor가 아닌 그 값을 가져올 때
loss.data[0]등의 표현식은 에러를 뱉는 경우가 많다. 이는 0.4 이후 버전의 PyTorch에서는loss.item()으로 그 값을 가져오도록 변경되었기 때문이다.- Pytorch의 loss는 이전에는
Variable에 할당된size=(1, )의 tensor였지만 이제는 scalar 형태이다.
- Pytorch의 loss는 이전에는
댓글로 문의하시면 확인 후 포스팅에 추가 가능합니다.