Adversarial AutoEncoder (AAE) 설명
23 Aug 2020 | Machine Learning Paper_Review Bayesian_Statistics목차
- 1. Adversarial Autoencoders Paper Review
- 1.1. Introduction
- 1.2. Adversarial Autoencoders
- 1.3. Likelihood Analysis of Adversarial Autoencoders
- 1.4. Supervised Adversarial Autoencoders
- 1.5. Semi-Supervised Adversarial Autoencoders
- 1.6. Unsupervised Clustering with Adversarial Autoencoders
- 1.7. Dimentionality Reduction with Adversarial Autoencoders
- 1.8. Conclusion
- 2. 핵심 내용
- 3. Tensorflow로 구현
- Reference
본 글에서는 VAE와 GAN을 결합한 Adversarial Autoencoder (이하 AAE)에 대한 논문을 리뷰하면서 이론에 대해 설명하고 이를 Tensorflow로 구현하는 과정을 보여줄 것이다. 이 알고리즘을 이해하기 위해서는 앞서 언급한 2가지 알고리즘에 대해 숙지하고 있어야 하며, VAE에 대해 알고 싶다면 이 글을, GAN에 대해 알고 싶다면 이 글을 참조하길 바란다.
1. Adversarial Autoencoders Paper Review
1.1. Introduction
오디오, 이미지, 영상 등과 같은 rich distribution을 포착하기 위해 Scalable한 생성 모델을 구성하는 것은 머신러닝에서도 굉장히 중요하고도 어려운 문제로 여겨진다. RBM, DBNs, DBM 등은 MCMC 기반의 알고리즘으로 학습되었다. 이러한 방법론들은 학습이 진행될수록 부정확하게 Log Likelihood의 Gradient를 포착하는 경향을 보였다. 왜냐하면 Markov Chain에서 온 Sample들은 여러 Mode를 빠르게 혼합하지 못하기 때문이다.
최근에는 이 대신 Direct Back-propagation을 이용하여 이 같은 단점을 극복한 VAE, GAN과 같은 알고리즘이 제안되었다.
본 논문에서는 autoencoder를 생성 모델로 변환하는 AAE라는 알고리즘을 제안할 것이다. 우리의 모델에서 이 autoencoder는 autoencoder의 Latent Representation의 Aggregated Posterior를 Arbitrary Prior에 연결하는 2개의 목적함수 (Traditional Reconstruction Error Criterion, Adversarial Training Criterion)로 학습을 진행할 것이다. 본 논문에서는 이러한 학습 방법이 VAE의 학습과 강력한 연관성을 보여준다는 것을 보여줄 것이다. Encoder가 데이터 분포를 Prior 분포로 변환하는 방법에 대해 학습하고 Decoder는 Imposed Prior를 데이터 분포에 매핑하는 Deep 생성 모델을 학습하게 된다.
1.1.1. Generative Adversarial Networks
GAN은 생성 모델 G와 판별 모델 D라는 2개의 신경망 사이의 Min-Max 적대적 게임을 구축하는 프레임워크이다. 판별 모델 $D(x)$ 는 데이터 공간의 포인트 $\mathbf{x}$ 가 실제 데이터 분포 (Positive Samples) 로 부터 추출되었는지를 계산하는 신경망이다. 생성자는 $G(\mathbf{z})$ 라는 함수를 사용하게 되는데, 이 함수는 Prior $p(\mathbf{z})$ 로부터 추출된 Sample $\mathbf{z}$ 를 데이터 공간에 연결시키는 역할을 한다. $G(\mathbf{z})$ 는 최대한 판별 모델로 하여금 Sample이 실제 데이터 분포로부터 추출되었다고 믿게 만드는, 속이는 역할을 하게 된다. 이 생성자는 x에 대하여 $D(x)$ 의 Gradient를 레버리지하여 학습된다. 그리고 이를 활용하여 파라미터를 조정한다. 이 게임의 해는 아래와 같이 표현할 수 있다.
alternating SGD를 이용하여 2단계로 학습이 진행된다. 먼저 판별자가 생성자로부터 생성된 가짜 Sample로부터 진짜 Sample을 구별하는 방법을 학습하고, 생성자는 이후 생성된 Sample을 통해 판별자를 속이는 방법을 학습한다.
1.2. Adversarial Autoencoders
잠시 기호에 대해 살펴보자.
\[p(\mathbf{z}), q(\mathbf{z}|\mathbf{x}), p(\mathbf{x}|\mathbf{z})\]위 기호는 차례대로 1) Code에 투사하고 싶은 Prior 분포, 2) Encoding 분포, 3) Decoding 분포를 의미한다.
\[p_d (\mathbf{x}), p(\mathbf{x})\]위 기호는 차례대로 4) 실제 데이터 분포, 5) Model 분포를 의미한다. Encoding 함수는 autoencoder의 (잠재 표현) Hidden Code 벡터에 대한 Aggregated Posterior 분포를 아래와 같이 정의한다.
Adversarial Autoencoder는 Aggregated Posterior인 $q(\mathbf{z})$ 를 Arbitrary Prior인 $p(\mathbf{z})$ 와 매칭시킴으로써 regualarized 된다. 그렇게 하기 위해서 이 적대적 네트워크는 아래 그림과 같이 autoencoder의 Hidden Code 벡터의 상위에 추가된다.
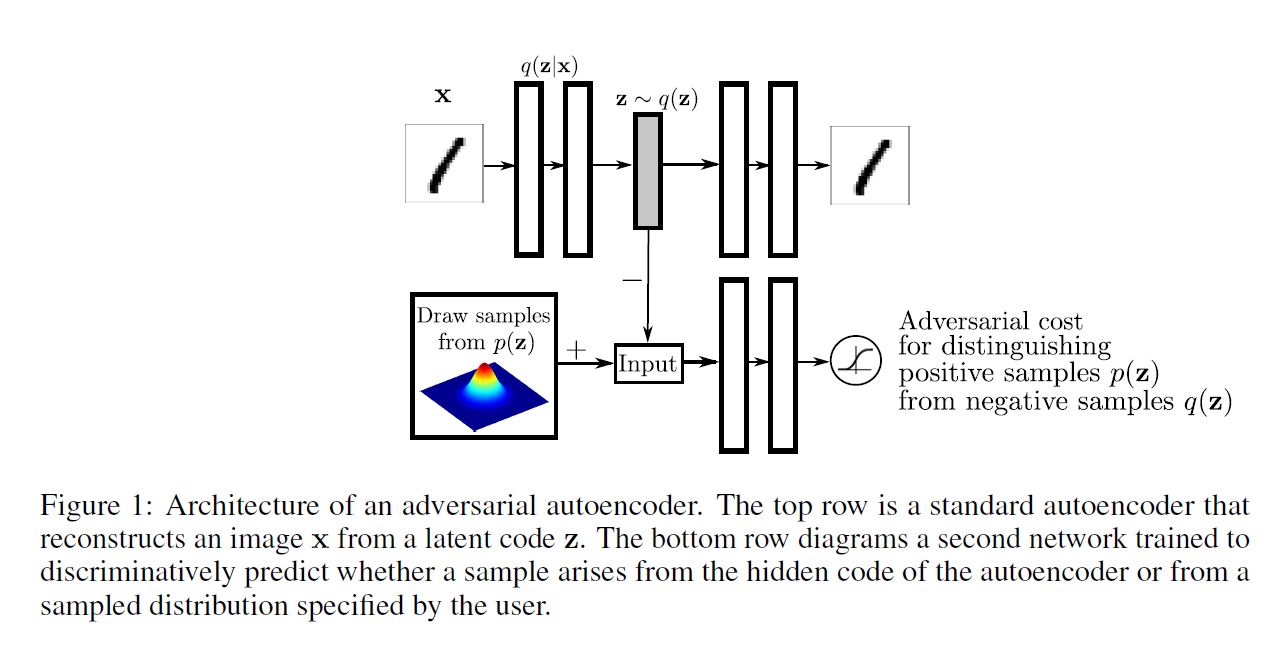
autoencoder는 그동안 Reconstruction Error를 최소화한다. 적대적 네트워크의 생성자는 사실 autoencoder의 encoder이다.
Encoder는 Hidden Code인 $q(\mathbf{z})$ 가 실제 Prior 분포 $p(\mathbf{z})$ 로부터 왔다고 판별 모델을 착각하게 만들어 Aggregated Posterior 분포가 판별 모델을 속이도록 만든다.
적대적 네트워크와 autoencoder 모두 2단계를 통해 SGD로 결합하여 학습된다. (Reconstruction 단계 Regularization 단계) Reconstruction 단계에서 autoencoder는 Encoder와 Decoder가 Input에 대한 Reconstruction Error를 최소화하도록 업데이트하게 된다. Regularization 단계에서 적대적 네트워크는 먼저 판별 모델이 진짜 Sample을 구별하도록 업데이트한 후, 생성자가 판별 네트워크를 속이도록 업데이트를 진행한다.
이러한 학습과정이 끝나면, autoencoder의 Decoder는 투사된 Prior인 $p(\mathbf{z})$ 를 실제 데이터 분포에 매핑하는 생성 모델을 정의하게 된다.
AAE의 Encoder를 정의하는 방법에는 다음과 같이 3가지가 존재한다.
1) Deterministic
Encoder가 $\mathbf{x}$ 의 deterministic 함수라고 가정해보자. 그렇다면 이 때의 Encoder는 가장 기본적인 형태의 autoencoder의 Encoder과 유사할 것이고 $q(\mathbf{z})$ 내부의 Stochasticity는 오직 실제 데이터 분포 $p_d (\mathbf{x})$ 에서만 찾을 수 있게 된다.
2) Gaussian Posterior
Encoder가 Encoder 네트워크에 의해 예측된 평균과 분산을 따르는 정규 분포라고 가정해보자.
이 때 $q(\mathbf{z})$ 의 Stochasticity는 실제 데이터 분포와 Encoder의 결과의 정규 분포의 Randomness 모두에서 나온다. VAE에서 보았듯이 Encoder 네트워크의 Back-propagation은 Reparametrization Trick을 통해 이루어진다.
3) Universal Approximator Posterior
AAE의 Encoder네트워크가 정규 분포와 같은 고정된 분포에서 추출한 Random Noise $\eta$ 와 Input $\mathbf{x}$ 의 함수 $f(\mathbf{x}, \eta)$ 라고 해보자. 우리는 여러 $\eta$ 를 Sampling 한 뒤 이에 따른 $f(\mathbf{x}, \eta)$ 를 평가하여 아래와 같은 (Encoder) 임의의 사후 분포를 추출할 수 있다.
우리는 Aggregated Posterior인 $q(\mathbf{z})$ 를 아래와 같이 표현할 수 있을 것이다.
\[q(\mathbf{z|x}) = \int_{\eta} q(\mathbf{z|x}, \eta) p_{\eta} (\eta) d \eta\] \[\rightarrow q(\mathbf{z}) = \int_{\mathbf{x}} \int_{\eta} q(\mathbf{z|x}, \eta) p_d(\mathbf{x}) p_{\eta} p_{\eta}(\eta) d\eta d\mathbf{x}\] \[q(\mathbf{z|x})\]이 때 위와 같은 Posterior는 더 이상 Gaussian일 필요가 없고, Encoder는 Input $\mathbf{x}$ 가 주어졌을 때 어떠한 임의의 사후 분포도 학습할 수 있다. Aggregated Posterior $q(\mathbf{z})$ 로부터 Sampling을 하는 효과적인 방법이 존재하기 때문에, 적대적 학습 과정은 Encoder 네트워크 $f(\mathbf{x}, \eta)$ 를 통한 직접적인 Back-propagation으로 $q(\mathbf{z})$ 를 $p(\mathbf{x})$ 에 연결할 수 있다.
지금까지 확인한 것처럼, 위 Posterior를 여러 다른 종류로 선택하게 되면 이는 또 다른 학습 Dymamics를 가진 다른 종류의 모델로 귀결된다. 예를 들어 1) Deterministic Case에서 네트워크는 데이터 분포로부터 Stochasticity를 뽑아내서 $q(\mathbf{z})$ 를 $p(\mathbf{x})$ 와 매칭시켜야 한다. 그러나 데이터의 경험적 분포가 학습 데이터 셋에서 고정되어 있기 때문에 Mapping이 Deterministic하면 부드럽지 못한 $q(\mathbf{z})$ 를 만들지도 모른다.
하지만 나머지 2개의 케이스에서는 네트워크가 Stochasticity의 추가적인 원천에 접근할 수 있기 때문에 이는 $q(\mathbf{z})$ 를 부드럽게 만들어 Adversarial Regularization 단계에서 개선이 이루어진다. 그럼에도 불구하고, 굉장히 광범위한 Hyper-parameter Search를 통해서 우리는 Posterior의 각 경우에 맞는 유사한 Test-Likelihood를 얻을 수 있었고 따라서 지금부터 본 논문에서는 Posterior의 Deterministic한 버전을 통해서 논의를 전개해 나가도록 할 것이다.
1.2.1. Relationship to Variational Autoencoders
VAE에서는 KL divergence 페널티를 사용하여 autoencoder의 Hidden Code 벡터에 Prior 분포를 투사하지만, Hidden Code의 Aggregated Posterior를 Prior 분포에 매칭시키는 적대적 학습 과정을 사용할 것이다. VAE는 아래와 같이 $\mathbf{x}$ 의 Negative Log-Likelihood에 대한 상한선을 최소화한다.
첫 번째 항은 Reconstruction 항으로, 나머지 항은 Regularization 항으로 생각할 수 있다. 만약 Regularization 항이 없다면 모델은 단순히 Input을 재현하는 기본적인 autoencoder의 형태를 취할 것이다. 두 번째 항이 사후 분포의 분산을 크게 만든다면, 세 번째 항은 Aggregated Posterior $q(\mathbf{z})$ 와 Prior $p(\mathbf{z})$ 사이의 Cross-Entropy를 최소화한다.
위 목적함수에서 KL divergence 또는 Cross-Entropy 항은 $q(\mathbf{z})$ 가 $p(\mathbf{z})$ 의 Modes를 고르도록 만든다. AAE에서 우리는 두 번째 두 항을 $q(\mathbf{z})$ 가 $p(\mathbf{z})$ 의 전체 분포와 매칭되게 하는 적대적 학습 과정으로 대체하였다.
본 섹션에서 우리는 구체적인 Prior 분포 $p(\mathbf{z})$ 를 Coding 분포에 투사하는 능력에 대해 AAE와 VAE를 비교해볼 것이다.
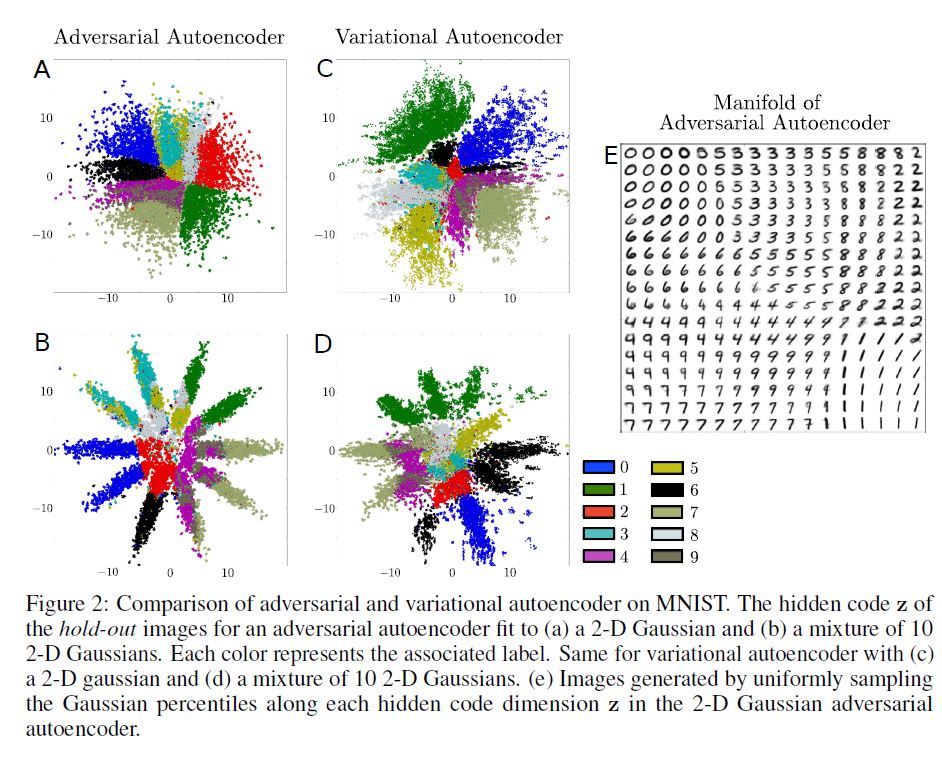
위 그림에서 E부분은 MNIST 숫자 데이터 셋을 학습한 AAE로부터 테스트 데이터의 Coding Space $\mathbf{z}$ 를 보여주며, 이 때 구형의 2차원 Gaussian Prior 분포가 Hidden Codes $\mathbf{z}$ 에 투사되었다.
A부분을 보면, 학습된 Manifold는 날카로운 변화를 보이는데 이는 Coding Space가 채워져 있고 ‘구멍’은 존재하지 않음을 의미한다. 실제로 Coding Space의 날카로운 변화는 $\mathbf{z}$ 내부에서 덧붙여져 생성된 이미지들이 데이터 Manifold 위에 있음을 의미한다.
반대로 C부분을 보면, VAE의 Coding Space는 AAE의 그것과 같은 구조를 보인다는 것을 확인할 수 있다. 이 경우 VAE가 대체로 2차원의 정규 분포의 형태와 일치한다는 것을 알 수 있는데, 그러나 어떠한 데이터 포인트도 Coding Space의 일부 Local Region에 매핑되지 않은 것을 볼 때 VAE는 AAE 만큼 데이터 Manifold를 잘 포착하지 못했다는 것을 알 수 있다.
B, D 부분을 보면 AAE와 VAE의 Coding Space의 투사된 분포가 10개의 2차원 Gaussian의 혼합임을 확인할 수 있다. AAE는 성공적으로 Aggregated Posterior를 Prior 분포에 매칭시켰다. 반대로 VAE는 10개의 Gaussian 혼합과는 구조적으로 다른 결과를 보여주는데, 이는 VAE가 앞서 언급하였듯이 분포의 Modes를 매칭시키는 데 집중하기 때문인 것으로 파악된다.
VAE에서 Monte-Carlo Sampling로 KL divergence를 Back-propagate하기 위해서는 Prior 분포의 정확한 함수 형태를 알고 있어야 한다. 그러나 AAE에서는 $q{\mathbf{z}}$ 를 $p(\mathbf{z})$ 에 매칭시키기 위해 Prior 분포로부터 Sampling만 할 수 있으면 된다는 점이 VAE와 AAE의 큰 차이이다.
1.2.3 절에서 우리는 AAE가 분포의 정확한 함수 형태를 알지 못한다 하더라도 (Swiss Roll 분포와 같이) 복잡한 분포를 투사할 수 있음을 증명할 것이다.
1.2.2. Relationship to GANs and GMMNs
(생략)
1.2.3. Incorporating Label Information in the Adversarial Regularization
데이터에 Label이 존재하는 경우 우리는 학습 과정에서 이 정보를 활영하여 더 나은 형태의 Hidden Code의 분포를 얻을 수 있다. 본 섹션에서 우리는 autoencoder의 잠재 표현을 규제하기 위해 부분적 또는 완전한 Label 정보를 활용하는 방법에 대해 설명할 것이다. 이러한 구조를 살펴보기 위해 1.2.1 절에서 확인하였던 B그림을 참조해보자. 이 때 AAE는 10개의 2차원 Gaussian의 혼합에 적합한 것으로 보인다. 지금부터 우리는 이 정규분포의 혼합의 각 Mode가 MNIST의 1개의 Label을 표현한다는 것을 보이도록 할 것이다.
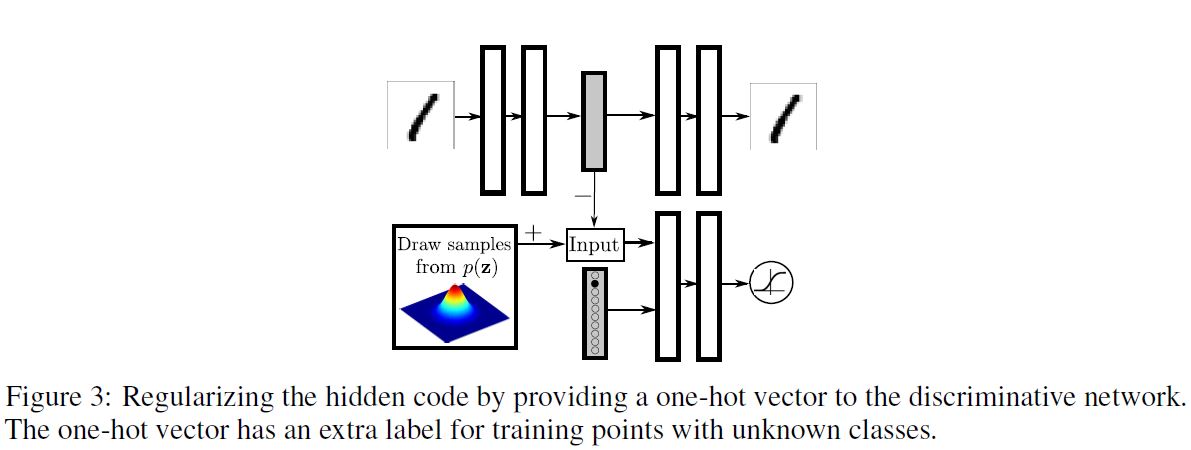
위 그림은 준지도 학습에 관한 학습 과정을 보여준다. 판별 네트워크의 Input에 One-Hot 벡터가 추가되어 분포의 Mode에 Label이 개입하도록 하였다. 이 One-Hot 벡터는 Class Label이 주어졌을 때 판별 네트워크의 적절한 결정 범위를 선택하는 스위치 역할을 하게 된다.
만약 Label이 존재하지 않을 경우 이 One-Hot 벡터는 다른 Class를 갖게 된다. 예를 들어, 10개의 2차원 Gaussian 혼합을 투사하는 경우, One-Hot 벡터는 11개의 Class를 갖게 될 것이다.
첫 10개의 Class의 각각은 적절한 개별 Mixture Component를 위한 결정 범위를 선택하게 된다. 모델에 Label이 없는 데이터 포인트가 주어졌을 때, Extra Class가 등장하여 정규 분포의 Full Mixture를 위한 결정 범위를 선택하게 된다.
AAE 학습의 Positive 단계에서 우리는 One-Hot 벡터를 통해 판별자에게 Mixture Component의 Label에 대한 정보를 제공한다.
Label이 없는 경우를 위한 Positive Sample은 특정 Class가 아닌 Gaussian의 Full Mixture로부터 오게 된다. Negative 단계에서 우리는 One-Hot 벡터를 통해 판별자에게 학습 이미지의 Label을 제공한다.
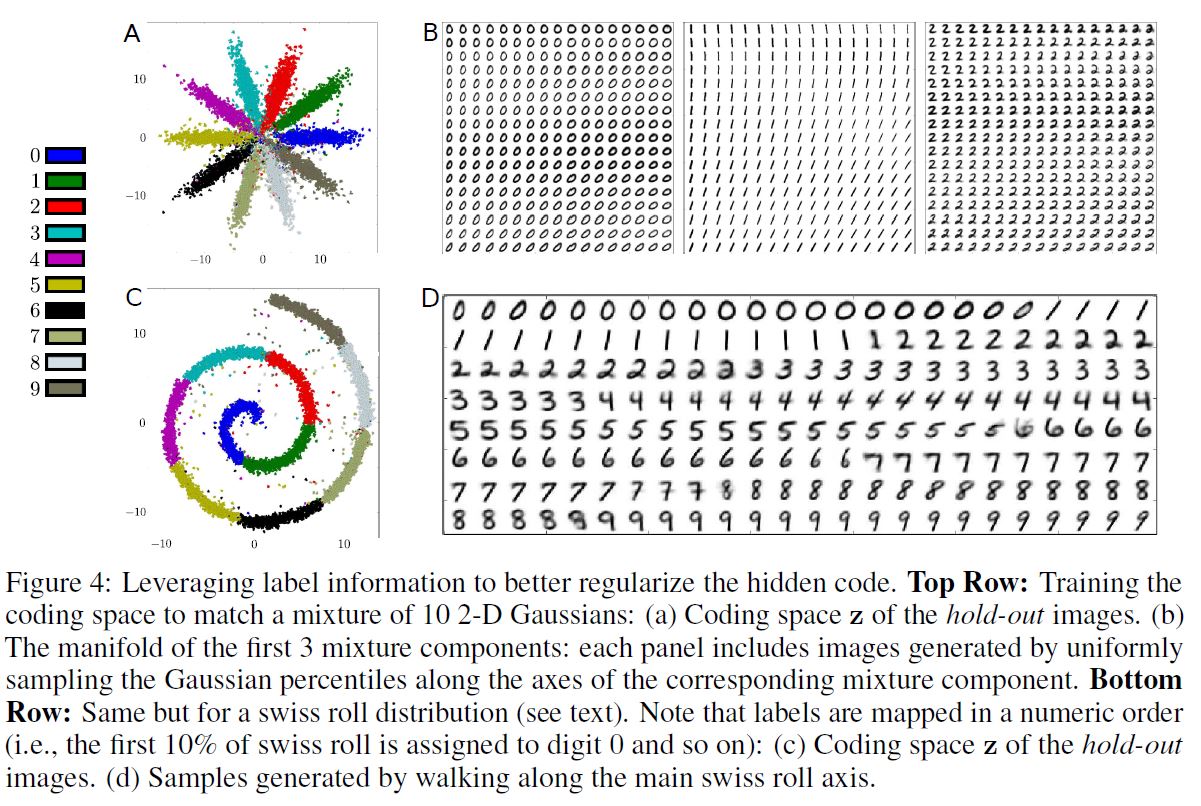
위 그림의 A 부분을 보면, 10K labeled MNIST 예시와 40K unlabeled MNIST 예시로 학습되었고, 10개의 2차원 Gaussian의 혼합 Prior로 학습된 AAE의 잠재 표현을 보여주고 있다. 이경우 Prior의 i번째 Mixture Component는 준지도 방식으로 i번째 Class에 할당되어 있다.
B 부분을 보면, 첫 번째 3개의 Mixture Component의 Manifold를 확인할 수 있다. Class와 독립적으로 각 Mixture Component 안에 Style Representation이 일관적으로 표현되어 있음을 알 수 있다. 예를 들어 B 부분의 좌상단 부분을 보면 Upright 필기 스타일로, 우하단을 보면 기울어진 스타일로 표현되어 있음을 알 수 있다.
이 방법은 Parametric 형식 없이고 임의의 표현으로 확장될 수 있다. C 부분은 Coding Space $\mathbf{z}$ 를 묘사하고 있고, D 부분은 잠재 공간의 Swiss Roll 축을 따라 생성된 이미지를 강조하고 있다.
1.3. Likelihood Analysis of Adversarial Autoencoders
이전 섹션에서 소개되었던 실험은 오직 질적인 결과만을 보여주었다. 이번 Chapter에서는 MNIST와 Toronto Face 데이터셋에 기반하여 hold-out 이미지를 생하는 모델의 Likelihood를 비교하여 데이터 분포를 포착하는 생성 모델로서 AAE의 성능을 평가해볼 것이다.
우리는 MNIST와 TFD에 AAE를 학습시켰는데, 이 때 모델은 근본적인 Hidden Code에 고차원적 정규 분포를 투사한다. 아래 그림은 데이터셋의 일부를 가져온 것이다.

AAE의 성능을 평가하기 위해 hold-out 테스트셋을 대상으로 Log Likelihood를 계산하였다. 사실 Likelihood를 사용하여 평가를 하는 방식은 그리 직관적이지는 못한데, 왜냐하면 사실 이미지의 확률을 직접적으로 계산한다는 것은 불가능하기 때문이다. 따라서 우리는 논문1, 논문2, 논문3 에 제시되었던 것처럼 True Log Likelihood의 Lower Bound를 계산하였다.
우리는 모델이 생성한 10,000개의 Sample에 대해 Gaussian Parzen Window (Kernel Density Estimator)를 계산하였고, 이 분포 하에서 테스트 데이터의 Likelihood를 계산하였다. Parzen Window의 자유 파라미터인 $\sigma$ 는 CV를 통해 선택되었다. 다음은 테스트 결과이다.
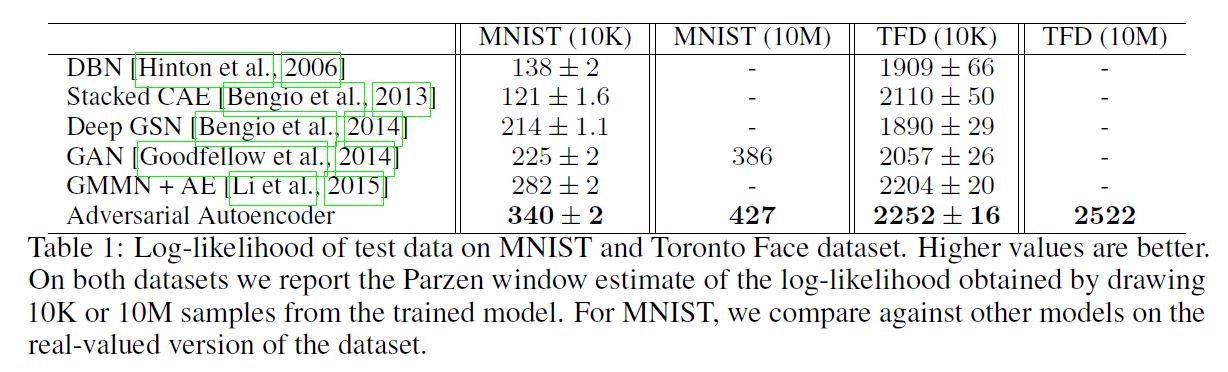
(중략)
1.4. Supervised Adversarial Autoencoders
준지도 학습은 머신러닝에서 오래된 개념적인 문제이다. 최근에 생성 모델들은 준지도 학습에 있어서 유명한 방법론들이 외덨는데, 왜냐하면 이러한 모델들은 원칙에 의거한 방법으로 Variation의 많은 다른 잠재 요인들로부터 Class Label 정보를 구분해낼 수 있었기 때문이다.
이번 Chapter에서 우리는 먼저 완전한 지도학습 시나리오에 초점을 맞추고 이미지의 Style 정보로부터 Class Label 정보를 분리해내는 AAE의 구조에 대해 논할 것이다. 이후 우리는 이러한 구조를 1.5 절에서 준지도 학습 세팅으로 확장해볼 것이다.
우리는 Label 정보를 통합하는 측면에서, Label의 One-Hot 벡터 인코딩을 Decoder에 제공하기 위해 네트워크 구조를 변경하였다. Decoder는 Label을 식별하는 One-Hot 벡터와 이미지를 재구성하는 Hidden Code $\mathbf{z}$ 를 사용한다. 이러한 구조는 네트워크가 Hidden Code $\mathbf{z}$ 에 있는 Label과 독립적인 모든 정보를 유지하도록 만든다.
아래 그림은 Hidden Code가 15차원 Gaussian으로 설정된 MNIST 데이터셋에 학습된 네트워크의 결과를 보여준 것이다.

위 그림의 각 행은 Hidden Code $\mathbf{z}$ 는 특정한 값으로 고정되어 있지만 Label은 구조적으로 탐색되었을 때 재구성된 이미지를 나타낸다. 행 속에서 재구성된 이미지들은 상당히 Style 측면에서 일관적인 것을 알 수 있다.
이 실험에서 One-Hot 벡터는 이미지의 central 숫자와 관련있는 Label을 의미한다. 각 행의 Style 정보는 제일 왼쪽과 제일 오른쪽의 숫자의 Label에 대한 정보를 담고 있는데, 왜냐하면 양 끝의 숫자들은 One-Hot 인코딩 속에서 Label 정보가 주어지지 않았기 때문이다.
1.5. Semi-Supervised Adversarial Autoencoders
이전 Chapter에 이어 이제 AAE를 준지도학습에 사용해 볼 것이다. 이 때 준지도학습은 오직 labeled된 데이터를 사용하여 얻어진 분류 성능을 개선하기 위해 unlabeled된 데이터의 generative description을 이용하는 것을 말한다. 구체적으로, 우리는 범주형 분포를 갖는 잠재 class 변수 $\mathbf{y}$ 와 정규 분포를 갖는 연속형 잠재 변수 $\mathbf{z}$ 로부터 데이터가 생성되었다고 가정할 것이다.
네트워크 구조를 변경하여 AAE의 추론 네트워크가 위와 같은 Encoder를 사용하여 범주형 Class 변수 $\mathbf{y}$ 와 연속형 잠재 변수 $\mathbf{z}$ 를 모두 예측하도록 해보자. 구조는 아래 그림과 같다.
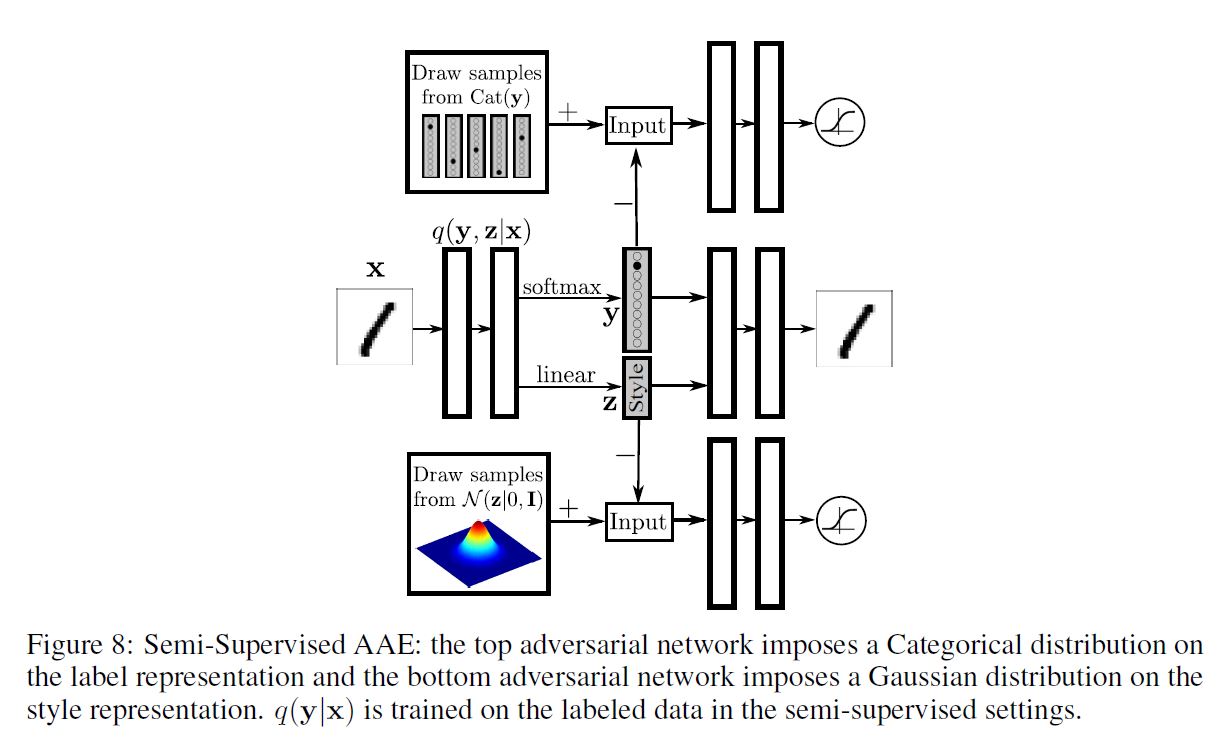
Decoder는 Class Label을 One-Hot 벡터로 활용하고 연속형 Hidden Code $\mathbf{z}$ 를 활용하여 이미지를 재구성한다. 첫 번째 적대적 네트워크는 범주형 분포를 Label Representation에 투사한다.
이 적대적 네트워크는 잠재 Class 변수 $\mathbf{y}$ 가 어떠한 Style 정보도 갖고 있지 않고 $\mathbf{y}$ 의 Aggregated Posterior 분포가 범주형 변수와 일치한다는 것을 보장한다. 두 번째 적대적 네트워크는 정규 분포를 Style Representation에 투사하여 잠재 변수 $\mathbf{z}$ 가 연속형 정규 변수라는 것을 보장한다.
적대적 네트워크와 autoencoder 모두 3가지 단계를 통해 학습된다. 3단계는 Reconstruction, Regularization, Semi-supervised Classification 단계를 의미한다.
Reconstruction 단계에서, autoencoder는 unlabeled 미니배치에 대해 Input의 Reconstruction Error를 최소화하기 위해 Encoder와 Decoder를 업데이트한다.
Regularization 단계에서 각 적대적 네트워크는 먼저 범주형 및 정규 Prior를 이용하여 생성된 진짜 Sample과 autoencoder에 의해 계산된 Hidden Code인 생성된 가짜 Sample를 구별하기 위해 판별 네트워크를 업데이트한다. 이후 적대적 네트워크는 판별 네트워크를 혼란시키기 위해 생성자를 업데이트한다.
마지막으로 Semi-supervised Classification 단계에서 autoencoder는 Labeled 미니배치에 대한 Cross-Entropy Cost를 최소화하기 위해 위 함수를 업데이트한다.
아래 표는 테스트 결과이다.
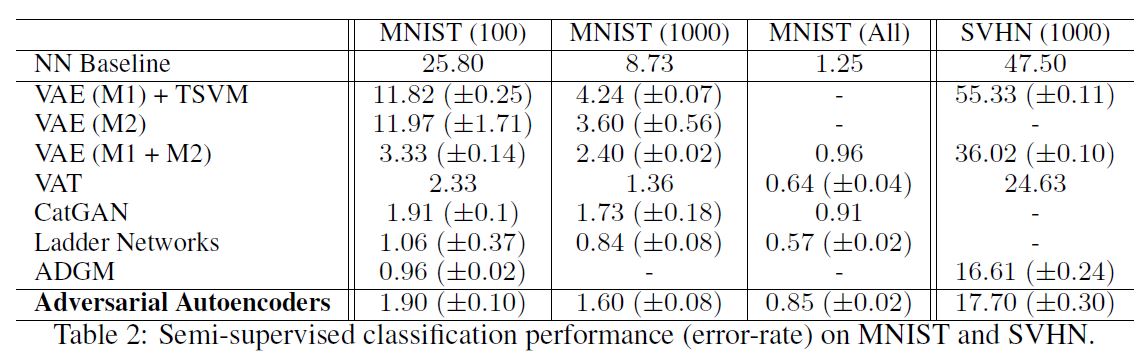
1.6. Unsupervised Clustering with Adversarial Autoencoders
어떠한 지도 없이 unlabeled 데이터로부터 강력한 표현을 학습할 수 있는 방법은 없을까? 이번 Chapter에서는 AAE가 오직 비지도 방법으로 연속형의 잠재 Style 변수로부터 이산적인 Class 변수를 구분해낼 수 있다는 것을 보여줄 것이다.
네트워크 구조는 사실 이전 Chapter에서 보았던 것과 유사하다. 다만, 이 때 준지도 분류 단계를 제거하였기 때문에 labeled 미니배치에 대해 네트워크를 학습하는 과정은 존재하지 않는다.
\[q(\mathbf{y|x})\]또 다른 점은, 위 추론 네트워크가 데이터가 속하는 클러스터를 의미하는 카테고리의 수만큼의 차원을 갖는 One-Hot 벡터를 예측하는 데 사용된다는 것이다.

위 그림은 클러스터의 수가 16일 때 MNIST 데이터셋에 대한 AAE의 클러스터링 성능을 보여준다. 각 행의 첫 번째 이미지는 클러스터 Head로, Style 변수를 0으로 고정하고 Label 변수를 1-of-16 One-Hot 벡터로 설정하여 생성된 숫자이다. 나머지 이미지들은 추론 네트워크에 기반하여 상응하는 카테고리로 배정된 테스트 데이터셋 이미지이다. 우리는 AAE가 몇몇 이산적 Style을 Class Label로서 포착한 것을 알 수 있다. 예를 들어 클러스터 11, 16을 보면 6과 1이 기울어져서 클러스터 10, 15와 다른 클러스터로 분류하였다. 또 클러스터 4, 6을 보면 같은 숫자 2라도 Style에 따라 다른 클러스터로 분류되어 있음을 알 수 있다.
AAE의 비지도 클러스터링 성능을 평가하기 위해 실험을 진행하였다. 평가 방법은 다음과 같다. 학습이 끝나면 각 클러스터 i에 대해 아래와 같은 식을 최대화하는 Validation Example $x_n$ 을 찾는다.
이후 $x_n$의 Label을 클러스터 i에 존재하는 모든 포인트에 할당한다. 그리고 나서 각 클러스터에 배정된 Class Label에 기반하여 테스트 에러를 계산한다. 그 결과는 다음과 같다. Cluster의 개수가 증가할 수록 에러는 감소하는 것을 알 수 있다.

1.7. Dimentionality Reduction with Adversarial Autoencoders
고차원 데이터의 시각화는 많은 분야에서 굉장히 중요한 문제이다. 왜냐하면 데이터의 생성 과정에 대한 이해를 촉진하고 분석가로 하여금 데이터에 대한 유용한 정보를 추출할 수 있도록 만들어주기 때문이다. 데이터 시각화의 유명한 방법은 유사한 개체에 상응하는 가까운 데이터 포인트에 존재하는 저차원의 Embedding을 학습하는 것이다. 지난 10년간 t-SNE와 같은 많은 비모수적 차원 축소 기법이 제안되었다. 이러한 방법의 큰 단점은 새로운 데이터 포인트를 위한 Embedding을 찾기 위해 사용될 수 있는 모수적 Encoder가 존재하지 않는다는 것이다. autoencoder는 이러한 Embeddding에 필요한 비선형적 Mapping을 제공해줄 수 있는 흥미로운 대안이지만, non-regularized autoencoder는 manifold를 많은 domain으로 분리해버려 유사한 이미지에 대한 다른 Code를 만들어 버리는 문제점을 갖고 있다.
이번 Chapter에서는 우리는 AAE를 차원 축소와 데이터 시각화를 위한 기법으로 소개할 것이다. 이 알고리즘에서 Adversarial Regularization은 유사한 이미지들의 Hidden Code를 서로 붙여주고 autoencoder에 의해 학습된 Embedding에서 전형적으로 맞닥드리는 문제였던 manifold를 분리하는 현상을 방지한다.
우리는 $m$ 개의 Class Label이 존재하는 데이터셋을 갖고 있고, 우리는 이를 $n$ 차원으로 줄이고 싶다고 하자. 이 때 $n$ 은 시각화를 위해 2~3이 적당할 것이다. 모델의 구조를 아래와 같이 바꿔보자.
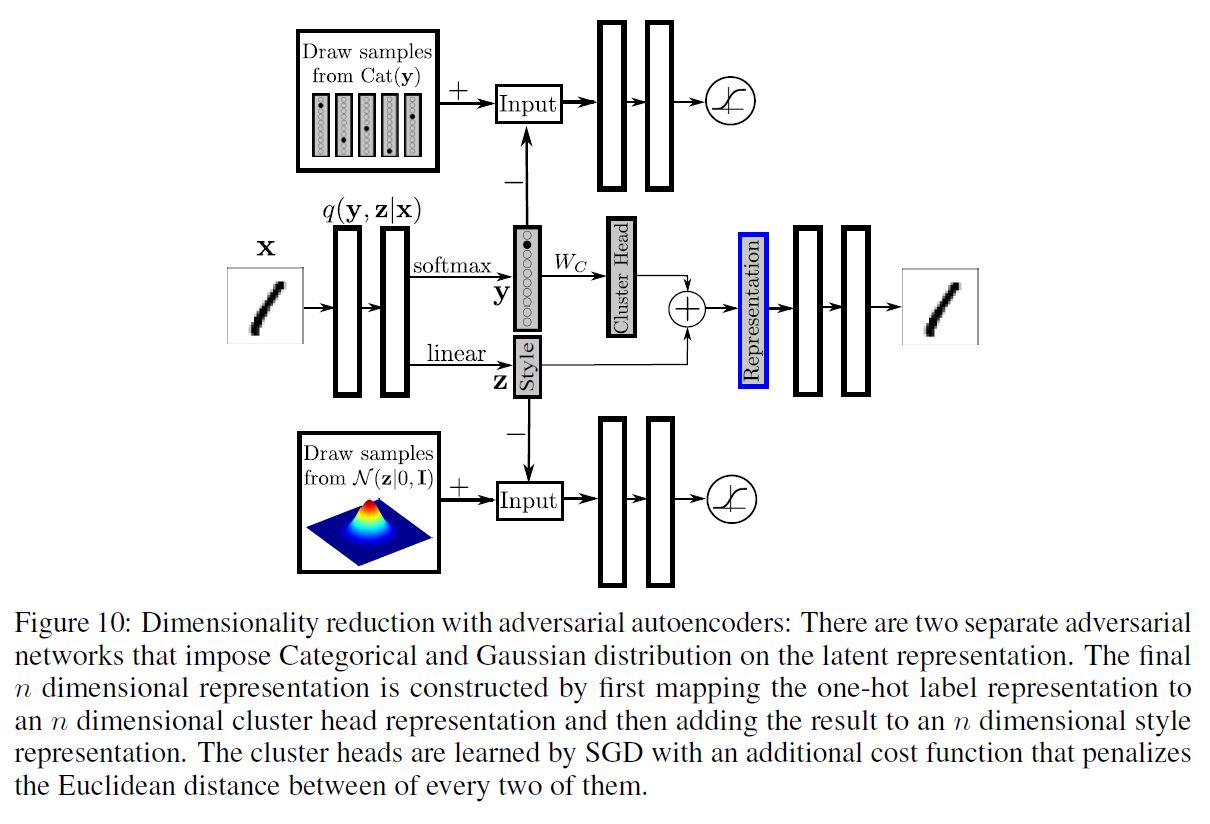
이 때 최종 Representation은 클러스터의 $n$ 차원의 분포 Representation을 $n$ 차원의 Style Representation에 추가하는 것으로 얻을 수 있다. 클러스터 Head Representation은 $m$ 차원의 One-Hot Class Label 벡터를 $m * n$ 크기의 행렬 $W_c$ 와 곱함으로써 얻을 수 있다. 이 때 $W_c$ 의 행은 SGD에 의해 학습된 $m$ 개의 클러스터 Head Representation을 나타낸다. 모든 2개의 클러스터 Head 사이의 유클리디안 거리를 규제하는 추가적인 Cost 함수를 소개할 것이다. 구체적으로 만약 유클리디안 거리가 어떤 threshold $\eta$ 보다 크면, Cost 함수는 0이 될 것이고, 그 반대의 경우라면 이 Cost 함수가 거리를 선형적으로 규제하게 될 것이다.
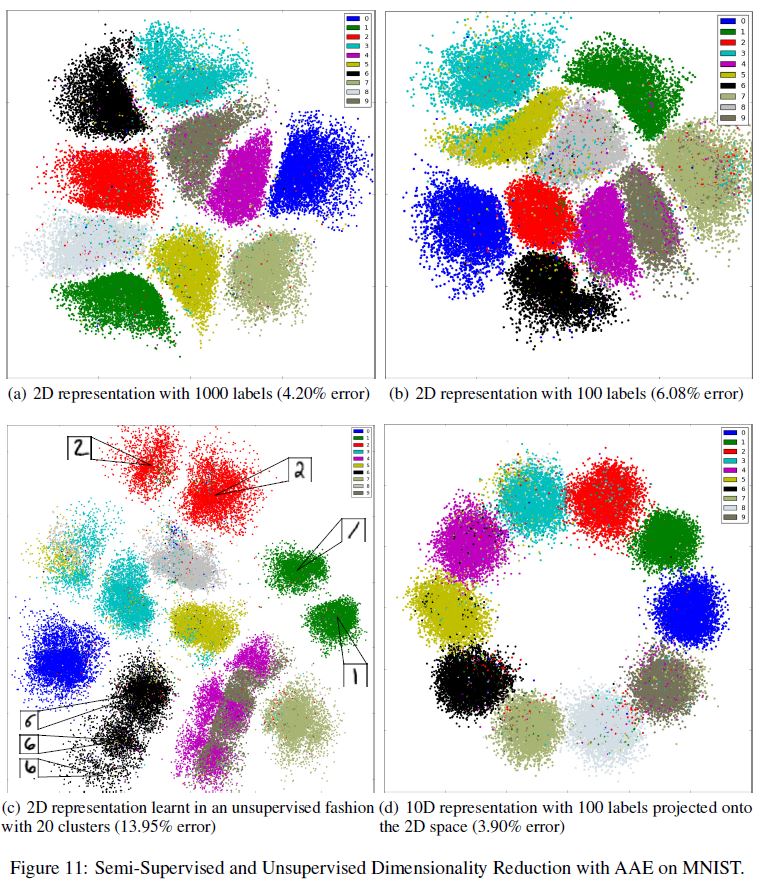
위 그림 중 a, b 부분을 보면 $m=10, n=2$ 일 때, 1000개/100개의 Label을 가진 MNIST 데이터셋에 대해 준지도학습 차원 축소의 결과를 보여준다. 각각 4.2, 6.08%의 준지도 분류 Error를 보여주면서 상당히 깨끗하게 숫자 클러스터를 분류한 것을 알 수 있다. 2차원 제약조건 때문에 분류 Error는 고차원 케이스만큼 좋지는 못하다. 그리고 각 클러스터의 Style 분포는 딱히 정규분포라고 보기 어렵다.
c 부분은 $n=2$ 차원, $m=20$ 개의 클러스터가 존재한다고 가정한 비지도 차원축소 결과를 나타낸다. 우리는 네트워크가 숫자 클러스터와 sub-클러스터의 깨끗한 구분을 보여준다는 것을 알 수 있다. 예를 들어 네트워크는 2개의 다른 클러스터를 숫자 1(초록 클러스터)에 할당하였는데, 이는 그 숫자가 곧거나 기울어져있는 것에 따라 결정되었다. 이는 빨간 클러스터인 숫자 2의 경우에도 동일하게 적용된다.
앞서 보았던 AAE의 구조는 또한 $n>2$ 일 때 더 큰 차원으로 이미지를 임베딩하는 데에 사용될 수 있다. 예를 들어 d 부분을 보면, 100개의 라벨이 존재할 때 $n=10$ 차원의 준지도 차원 축소의 결과를 보여준다. 이 경우 우리는 $W_c = 10 \mathbf{I}$ 로 고정했기 때문에 클러스터 Head는 10차원 simplex의 코너를 의미한다. Style Representation은 표준편차1의 10차원 정규 분포로 학습되었고, 최종 Representation을 구성하기 위해 클러스터 Head에 직접 추가되었다.
네트워크가 학습되면 10차원의 학습된 Representation을 시각화하기 위해, 10차원 Representation을 클러스터 Head가 2차원 원에 균일하게 위치하는 데이터 포인트에 mapping되는 2차원 공간에 mapping되도록 선형 변환을 사용하였다. 우리는 고차원 케이스에서 Style Representation이 정말 정규 분포를 갖는다는 것을 확인할 수 있다. 총 100개의 Label에서 이 모델은 3.9%의 분류 에러를 보여주었는데, 이는 1.5 Chapter에서 보여주었던 1.9%의 에러보다 좋지 못한 결과이다.
1.8. Conclusion
본 논문에서 우리는 확률론적 autoencoder에 있는 이산형/연속형 잠재 변수들을 위한 변분 추론 알고리즘으로서 GAN 프레임워크를 사용하였다. 이 방법은 AAE라고 명명하며, MNIST와 Toronto Face 데이터셋에 대해 경쟁력 있는 테스트 Likelihood를 얻은 생성 autoencoder로 정의할 수 있다. 우리는 이 방법이 어떻게 준지도 학습 시나리오로 확장될 수 있는지 보여주었으며 이 방법이 MNIST, SVHN 데이터셋에 대해 경쟁력있는 준지도 분류 성능을 갖는다는 것을 보여주었다. 최종적으로 우리는 이 AAE 알고리즘이 이미지의 Style과 Content를 구별하고 비지도 클러스터링이나 차원축소, 데이터 시각화 등에도 사용될 수 있다는 것을 증명하였다.
2. 핵심 내용
코드로 넘어가기 전에, AAE의 핵심에 대해서 한 번만 더 짚고 넘어가도록 하겠다.
위 식은 이 글에서 상세히 설명하였듯이, VAE의 목적함수이다. 이 때 KL-divergence는 일종의 규제 역할을 하게 되는데, 의미론적으로 보면 아래 두 분포를 유사하게 만드는 역할을 하게 된다.
Encoder와 Prior를 유사하게 만들어야 하는데, VAE에서는 이 두 분포에서 Sampling이 가능하고, numerical하게 계산이 가능해야 한다는 전제가 필수적이다. 그렇기 때문에 이들 분포로 정규 분포가 널리 사용되는 것이다.
AAE는 두 전제 중 2번째 전제를 불필요하게 만드는 알고리즘이다. 두 분포를 유사하게 만들기 위해 위와 같은 KL-divergence를 계산하는 것이 아니라 GAN으로 하여금 이 역할을 수행하게 만든 것이다. 즉, GAN이 KL-divergence를 대체한 것이다.
따라서 전체 Loss는 1) Autoencoder의 Reconstruction Loss, 2) Discriminator Loss, 3) Generator Loss 이렇게 3가지로 구분할 수 있다.
이제 Tensorflow로 구현을 시작해보자.
3. Tensorflow로 구현
논문을 자세히 읽어보았다면 이 알고리즘을 구현하는 방법은 꽤 다양하다는 것을 알 수 있을 것이다. 본 글에서는 MNIST 데이터셋을 이용하여 Supervised Adversarial Autoencoder를 구현해보겠다. 본 Chapter에서의 구현 방법은 굉장히 간단하고 분포를 변경하거나 Layer의 구조를 선택하는 등 변형에 있어 다소 불편하게 되어 있는데, 추후 글에서 불균형 학습을 해결하기 위해 AAE를 활용하는 방법에 대해 다루면서 개선된 코드를 제공하도록 하겠다.
autoencoder는 Deterministic하게 구성하였으며, Prior로는 정규 분포를 사용하였다. (논문에서는 Gaussian Mixture와 Swiss Roll 분포를 예로 들었다.) 모델 구조를 살펴보자.
class AAE(tf.keras.Model):
def __init__(self, latent_dim):
super(AAE, self).__init__()
self.latent_dim = latent_dim
self.encoder = tf.keras.Sequential(
[
tf.keras.layers.InputLayer(input_shape=(28*28 + 1)),
tf.keras.layers.Flatten(),
tf.keras.layers.Dense(units=512, activation='relu'),
tf.keras.layers.Dropout(rate=0.2),
tf.keras.layers.Dense(units=256, activation='relu'),
tf.keras.layers.Dropout(rate=0.2),
tf.keras.layers.Dense(units=64, activation='relu'),
tf.keras.layers.Dense(units=latent_dim),
])
self.decoder = tf.keras.Sequential(
[
tf.keras.layers.InputLayer(input_shape=(latent_dim+1)),
tf.keras.layers.Dense(units=64, activation='relu'),
tf.keras.layers.Dropout(rate=0.2),
tf.keras.layers.Dense(units=256, activation='relu'),
tf.keras.layers.Dropout(rate=0.2),
tf.keras.layers.Dense(units=512, activation='relu'),
tf.keras.layers.Dense(units=784),
])
self.discriminator = tf.keras.Sequential(
[
tf.keras.layers.InputLayer(input_shape=(latent_dim+1)),
tf.keras.layers.Dense(units=64, activation='relu'),
tf.keras.layers.Dropout(rate=0.2),
tf.keras.layers.Dense(units=128, activation='relu'),
tf.keras.layers.Dropout(rate=0.2),
tf.keras.layers.Dense(units=64, activation='relu'),
tf.keras.layers.Dropout(rate=0.2),
tf.keras.layers.Dense(units=1),
])
@tf.function
def encode(self, x, y):
inputs = tf.concat([x, y], 1)
z = self.encoder(inputs)
return z
@tf.function
def discriminate(self, z, y):
inputs = tf.concat([z, y], 1)
output = self.discriminator(inputs)
return output
@tf.function
def decode(self, z, y, apply_sigmoid=False):
inputs = tf.concat([z, y], 1)
logits = self.decoder(inputs)
if apply_sigmoid:
probs = tf.sigmoid(logits)
return probs
return logits
Discriminator의 마지막 Layer는 True와 Fake를 구별하기 위해 1개의 Node로 마무리하였다. Encoder의 결과물인 $\mathbf{z}$ 가 Fake z이며, Prior에서 나온 결과물이 True z에 해당한다.
AAE는 학습이 3단계로 이루어지기 때문에 Loss도 개별적으로 계산하는 것이 좋다. 아래 코드를 보면 이해가 될 것이다.
def compute_reconstruction_loss(x, x_logit):
# Reconstruction Loss
marginal_likelihood = tf.reduce_sum(x * tf.math.log(x_logit) + (1 - x) * tf.math.log(1 - x_logit), axis=[1])
loglikelihood = tf.reduce_mean(marginal_likelihood)
reconstruction_loss = -loglikelihood
return reconstruction_loss
def compute_discriminator_loss(fake_output, true_output):
# Discriminator Loss
d_loss_true = tf.reduce_mean(tf.nn.sigmoid_cross_entropy_with_logits(logits=true_output,
labels=tf.ones_like(true_output)))
d_loss_fake = tf.reduce_mean(tf.nn.sigmoid_cross_entropy_with_logits(logits=fake_output,
labels=tf.zeros_like(fake_output)))
discriminator_loss = d_loss_true + d_loss_fake
return discriminator_loss
def compute_generator_loss(fake_output):
# Generator Loss
generator_loss = tf.reduce_mean(tf.nn.sigmoid_cross_entropy_with_logits(logits=fake_output,
labels=tf.ones_like(fake_output)))
return generator_loss
이 때 x는 실제 데이터 Input을, x_logit은 autoencoder를 통과한 결과물이다. fake_output은 Encoder의 결과물인 z가 Discriminator를 통과한 후의 결과물이며, true_output은 Prior true_z가 Discriminator를 통과한 후의 결과물이다.
학습 함수는 아래와 같다. 이 때 기본적인 GAN의 특성상 Generator의 학습 속도가 느린 점을 반영하여 Generator는 2번 학습하도록 하였다.
@tf.function
def train_step(model, x, y, r_optimizer, d_optimizer, g_optimizer):
# Results
x = tf.reshape(x, [-1, 784])
y = tf.reshape(y, [-1, 1])
# Propagation
with tf.GradientTape() as tape:
z = model.encode(x, y)
x_logit = model.decode(z, y, True)
x_logit = tf.clip_by_value(x_logit, 1e-8, 1 - 1e-8)
reconstruction_loss = compute_reconstruction_loss(x, x_logit)
r_gradients = tape.gradient(reconstruction_loss, model.trainable_variables)
r_optimizer.apply_gradients(zip(r_gradients, model.trainable_variables))
with tf.GradientTape() as tape:
z = model.encode(x, y)
true_z = tf.random.normal(shape=(z.shape))
fake_output = model.discriminate(z, y)
true_output = model.discriminate(true_z, y)
discriminator_loss = compute_discriminator_loss(fake_output, true_output)
d_gradients = tape.gradient(discriminator_loss, model.trainable_variables)
d_optimizer.apply_gradients(zip(d_gradients, model.trainable_variables))
for _ in range(2):
with tf.GradientTape() as tape:
z = model.encode(x, y)
fake_output = model.discriminate(z, y)
generator_loss = compute_generator_loss(fake_output)
g_gradients = tape.gradient(generator_loss, model.trainable_variables)
g_optimizer.apply_gradients(zip(g_gradients, model.trainable_variables))
total_loss = reconstruction_loss + discriminator_loss + generator_loss
return total_loss
Epoch30, 잠재 차원은 4로하고, Discriminator의 학습률은 다소 낮게 설정하여 학습을 진행하여 보자. (Reference 2 강의 참조)
epochs = 30
latent_dim = 4
model = AAE(latent_dim)
r_optimizer = tf.keras.optimizers.Adam(1e-4)
d_optimizer = tf.keras.optimizers.Adam(1e-4/5)
g_optimizer = tf.keras.optimizers.Adam(1e-4)
# Train
for epoch in range(1, epochs + 1):
train_losses = []
for x, y in train_dataset:
total_loss = train_step(model, x, y, r_optimizer, d_optimizer, g_optimizer)
train_losses.append(total_loss)
print('Epoch: {}, Loss: {:.2f}'.format(epoch, np.mean(train_losses)))
Epoch 30 이후의 Loss는 126.8까지 감소하였다. 이전 글에서 보았던 Test 함수를 통해 결과물을 확인해보자. 위쪽 그림이 원본, 아래쪽 그림이 AAE의 결과물이다.

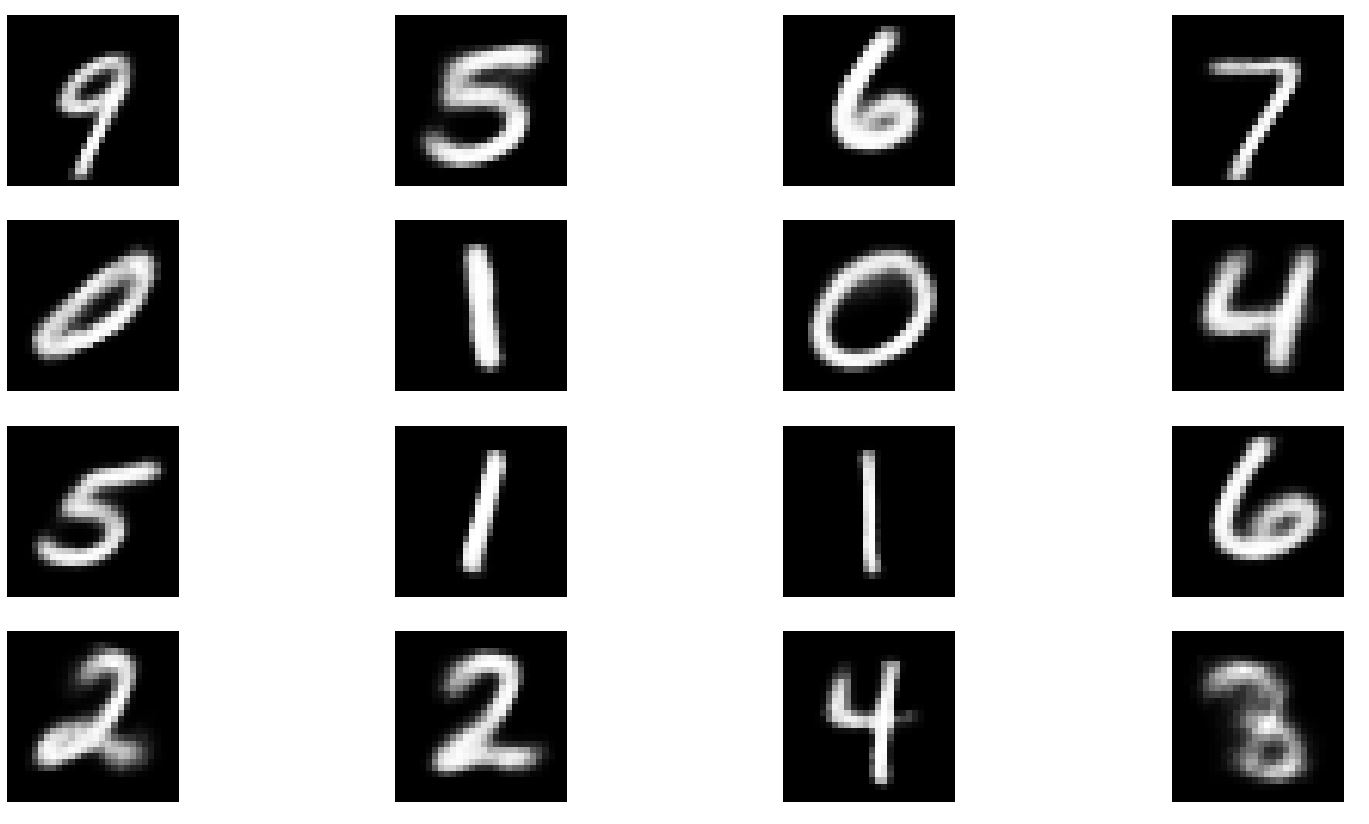
CVAE의 결과보다 더욱 선명한 결과를 보여준 점이 만족스럽다. 튜닝에 더욱 신경을 쓴다면 더욱 좋은 결과가 있지 않을까 생각해본다.
Reference
1) 논문 원본
2) 오토인코더의 모든 것

