Attentional Factorization Machines (AFM) 논문 리뷰 및 Tensorflow 구현
01 May 2020 | Machine_Learning Recommendation System AFM목차
- 1. Attentional Factorization Machines: Learning theWeight of Feature Interactions via Attention Networks 논문 리뷰
- 2. Tensorflow를 활용한 구현
본 글의 전반부에서는 먼저 Attentional Factorization Machines: Learning theWeight of Feature Interactions via Attention Networks 논문을 리뷰하면서 본 모델에 대해 설명할 것이다. 후반부에서는 Tensorflow를 이용하여 직접 코딩을 하고 학습하는 과정을 소개할 것이다. 논문의 전문은 이곳에서 확인할 수 있다.
1. Attentional Factorization Machines: Learning theWeight of Feature Interactions via Attention Networks 논문 리뷰
1.0. Absbract
FM은 2차원 피쳐 상호작용을 잘 통합하여 선형 회귀를 개선한 지도학습 알고리즘이다. 이 알고리즘은 효과적이긴 하지만, 모든 피쳐에 대해 같은 weight로 학습을 진행시킨다는 점에서 비효율적이다. 왜냐하면 종종 일부 피쳐는 학습에 있어 필수적이지 않은 경우가 있기 때문이다. 오히려 이러한 피쳐들의 존재는 모델의 성능을 떨어트릴 수 있다. 따라서 우리는 여러 피쳐 상호작용 속에서 중요한 피쳐들을 구분해내는 새로운 모델, Attentional Factorization Machine (AFM)을 소개한다.
1.1. Introduction
FM은 피쳐 상호작용의 중요성을 구분하는 능력이 부족하기 때문에(피쳐의 중요성을 파악하는 능력) suboptimal 문제에 빠질 수 있다. AFM은 이러한 문제를 해결하기 위해 도입한 모델이다.
1.2. Factorization Machines
FM 모델에 대한 설명은 이곳을 참조하길 바란다. 기호에 대해서만 설명을 추가하면, $v_i$는 피쳐 $i$에 대한 임베딩 벡터이며, $k$는 임베딩 크기를 의미한다.
1.3. Attentioanl Factorization Machines
1.3.1. Model
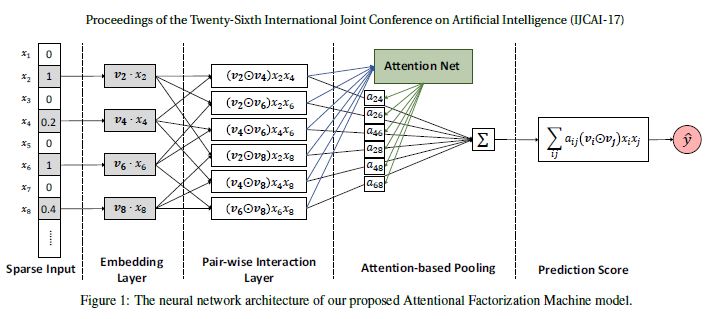
위 그림은 AFM의 구조를 보여준다. 선명히 보여주기 위해 그림에서는 선형 회귀 부분을 생략하였다. Input Layer와 Embedding Layer의 경우 FM과 같은 구조를 지니는데, Input 피쳐들은 sparse하게 이루어져있고 이들은 dense vector로 임베딩된다. 지금부터는 본 모델의 핵심인 pair-wise interaction layer과 attention-based pooling layer를 설명할 것이다.
Pair-wise Interaction Layer
상호작용을 포착하기 위해 내적을 사용하는 FM을 참고하여, 본 논문에서는 신경망 모델링에서 새로운 Pair-wise Interaction Layer를 제시한다. $m$개의 벡터를 $\frac{m(m-1)}{2}$개의 interacted 벡터로 만드는데, 이 때 각 interacted 벡터는 상호작용을 포착하기 위해 2개의 다른 벡터들의 원소곱으로 계산된다.
정확히 말하면, 피쳐 벡터 $x$의 0이 아닌 피쳐의 집합을 $\chi$라고 하자. 그리고 Embedding Layer의 결과물을 $\epsilon = {{v_i x_i}}_{i \in \chi} $라고 하자. 우리는 아래와 같이 Pair-wise Interaction Layer의 결과물을 아래와 같은 벡터의 집합으로 표현할 수 있다.
- $\odot$ 기호: 원소곱
- $ R_x = { (i, j) }_{i, j \in \chi, j>i} $
이 Layer를 정의하면서 우리는 FM을 신경망 구조로 표현할 있게 된다. 먼저 $f_{PI}(\epsilon)$를 sum pooling으로 압축한다음, Fully Connected Layer를 사용하여 prediction score에 투사(project)한다.
\[\hat{y} = p^T \sum_{(i, j) \in R_x} (v_i \odot v_j) x_i x_j + b\]- $p \in R^k$
- $b \in R$
위에서 등장한 p, b는 Prediction Layer의 weight과 bias이다. 물론 p=1, b=0으로 값을 고정한다면 이는 FM과 동일한 형상을 취하게 될 것이다.
Attention-based Pooling Layer
Attention의 기본 아이디어는, 여러 개의 부분이 압축 과정에 있어서 각각 다르게 기여하여 하나로 표현되게 만드는 것이다. interacted 벡터들의 가중 합을 수행하여 피쳐 상호작용에 대해 Attention 메커니즘을 적용하였다.
여기서 $a_{i, j}$는 피쳐 상호작용 $\hat{w}_{ij}$의 Attention Score이다.
Prediction Loss를 최소화하여 직접적으로 학습을 진행하여 $a_{i,j}$를 추정하는 것이 기술적으로는 맞게 느껴지지만, 학습 데이터에서 한 번도 동시에 등장한 적이 없는 피쳐들의 경우, 이들의 상호작용에 대한 Attention Score는 추정될 수 없다.
이러한 일반화 문제를 해결하기 위해 MLP를 통해 Attention Score를 파라미터화 하는 Attention Network를 추가하였다. 이 네트워크의 Input은 2개의 피쳐의 interacted 벡터인데, 이들의 상호작용 정보는 임베딩 공간에 인코딩된다.
\(e_{ij} = h^T ReLU(W (v_i \odot v_j) x_i x_j + b)\)
\(a_{ij} = \frac {exp(e_{ij})} { \sum_{(i, j) \in R_x} exp(e_{ij}) }\)
- $W \in R^{t*k}, b \in R^t, h \in R^t$
- $t$: Attention Network의 hidden layer의 크기(Attention Factor)
Attention Score는 softmax 함수를 통해 정규화된다. 이 Attention-based Pooling Layer의 결과물은 k 차원의 벡터로, 중요성을 구별하여 임베딩 공간에서의 모든 피쳐 상호작용을 압축한 것이다. 요약하자면, AFM 모델의 최종 공식은 아래와 같다.
모델 파라미터들은 $ w_0, w, v, p, W, b, h $이다.
1.3.2. Learning
AFM이 데이터 모델링의 관점에서 FM을 개선함에 따라 본 모델은 예측, 회귀, 분류, 랭킹 문제 등에 다양하게 적용될 수 있다. 목적 함수를 최적화하기 위해 SGD를 사용하였다. SGD 알고리즘 적용의 핵심은, 각 파라미터를 기준으로 예측 모델 AFM의 derivative를 구하는 것이다.
과적합 문제
FM보다 표현력이 뛰어난 AFM이기에 더욱 과적합 문제에 민감할 수 있다. 따라서 본 모델에서는 dropout과 L2 Regularization 테크닉이 사용되었다.
(후략)
2. Tensorflow를 활용한 구현
2.1. 데이터 준비
본 모델의 경우 Dataset에 대한 Domain 지식이 필요하다고 볼 수는 없지만, 학습을 진행하기에 앞서 기본적으로 직접 전처리를 해주어야 하는 부분들이 있다. One-Hot 인코딩 외에도, 본 모델은 앞서 논문 리뷰에서도 확인하였듯이 0이 아닌 값에 대해서만 Lookup을 수행하여 실제 학습 데이터를 사용하기 때문에 이에 대한 정보를 저장해야할 필요가 있다. 아래 예시를 잠시 살펴보면,
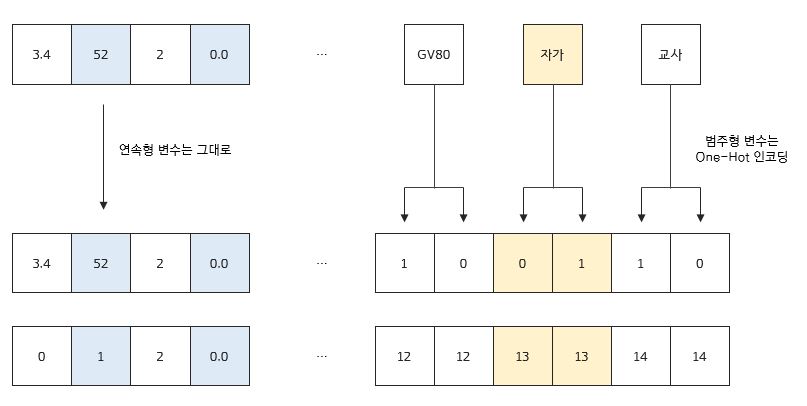
만약 연속형 변수 중에 0.0이라는 값이 존재하더라도 사실 이 값은 중요한 특성을 나타낼 수도 있다. 그러나 논문의 기본 논조대로라면, 0인 값이기 때문에 학습에서 제외되게 된다. 이렇게 0이라고 해서 중요한 값이 학습에서 제외되는 현상을 막기 위해 본 구현에서는 One-Hot 인코딩 이후의 데이터에 대하여 중요한 정보의 위치를 저장하는 masking 작업을 진행하게 된다.
데이터는 DeepFM 구현글에서 사용한 것과 동일하다. 데이터 전처리는 연속형 변수에 대해서는 MinMaxScale, 범주형 변수에 대해서는 One-Hot 인코딩만을 진행하게 된다.
2.2. Layer 정의
AFM 모델에서는 크게 3개의 Layer가 필요하다. Embedding Layer, Pairwise Interaction Layer, Attention Pooling Layer가 바로 그 3가지이다. Embedding Layer 부분은 이전 글(논문)들을 읽었다면, 굉장히 익숙하게 받아들여 질 것이다. 다만 이전 DeepFM 구현글에서는 하나의 Field에 대해 하나의 Embedding Row가 학습되었다면, 본 글에서는 하나의 Feature에 대해 하나의 Embedding Row가 학습되도록 코드를 수정하였다.
앞서 언급하였듯이 One-Hot 인코딩으로 생성된 0 값을 갖는 feature를 제외한 feature들만 실제 학습에 사용되는데(예를 들어 One-Hot 인코딩 이후에 0.2, 7.4, 0, 1, … 0, 1와 같은 데이터로 변환되었다면 실제 학습에 사용되는 데이터는 0.2, 7.4, 1, … 1이라는 뜻이다.)
위와 같은 논리를 구현하는 방법에는 여러가지가 있을 수 있겠지만 본 구현에서는 다음과 같은 논리를 따랐다.
1) 연속형 변수들은 모두 앞쪽에 배치한 후, 이들에게는 무조건 True Mask를 씌워 학습 데이터로 활용한다.
2) 범주형 변수들에 대해서는 0이 아닌 값들에 대해서 True Mask를 씌워 학습 데이터로 활용한다.
논리 자체는 간단하며, 아래 call 메서드에서 그 논리가 구현되어 있다.
import tensorflow as tf
import numpy as np
import config
class Embedding_layer(tf.keras.layers.Layer):
def __init__(self, num_field, num_feature, num_cont, embedding_size):
super(Embedding_layer, self).__init__()
self.embedding_size = embedding_size # k: 임베딩 벡터의 차원(크기)
self.num_field = num_field # m: 인코딩 이전 feature 수
self.num_feature = num_feature # p: 인코딩 이후 feature 수, m <= p
self.num_cont = num_cont # 연속형 field 수
self.num_cat = num_field - num_cont # 범주형 field 수
# Parameters
self.V = tf.Variable(tf.random.normal(shape=(num_feature, embedding_size),
mean=0.0, stddev=0.01), name='V')
def call(self, inputs):
# inputs: (None, p, k), embeds: (None, m, k)
batch_size = inputs.shape[0]
# 원핫인코딩으로 생성된 0을 제외한 값에 True를 부여한 mask(np.array): (None, m)
# indices: 그 mask의 indices
cont_mask = np.full(shape=(batch_size, self.num_cont), fill_value=True)
cat_mask = tf.not_equal(inputs[:, self.num_cont:], 0.0).numpy()
mask = np.concatenate([cont_mask, cat_mask], axis=1)
_, flatten_indices = np.where(mask == True)
indices = flatten_indices.reshape((batch_size, self.num_field))
# embedding_matrix: (None, m, k)
embedding_matrix = tf.nn.embedding_lookup(params=self.V, ids=indices.tolist())
# masked_inputs: (None, m, 1)
masked_inputs = tf.reshape(tf.boolean_mask(inputs, mask),
[batch_size, self.num_field, 1])
masked_inputs = tf.multiply(masked_inputs, embedding_matrix) # (None, m, k)
return masked_inputs
다음은 Pairwise Interaction Layer에 대한 설명이다. 만약 14개의 Row가 존재한다면 이에 대한 모든 조합을 구하여 91 = $14\choose2$ 개의 Row를 생성하는 Layer인데, 간단하게 생각해보면 아래와 같이 코드를 짜고 싶을 것이다.
from itertools import combinations
interactions = []
comb_list = list(range(0, num_field, 1))
for b in range(batch_size):
for i, j in list(combinations(self.comb_list, 2)):
interactions.append(tf.multiply(inputs[b, i, :], inputs[b, j, :]))
pairwise_interactions = tf.reshape(tf.stack(interactions),
(batch_size, -1, self.embedding_size))
하지만 위와 같이 loop를 돌리게 되면, 속도가 현저하게 느려져서 실 사용이 불가능하다. 따라서 이 때는 Trick이 필요한데, 그림으로 설명하면 아래와 같다.
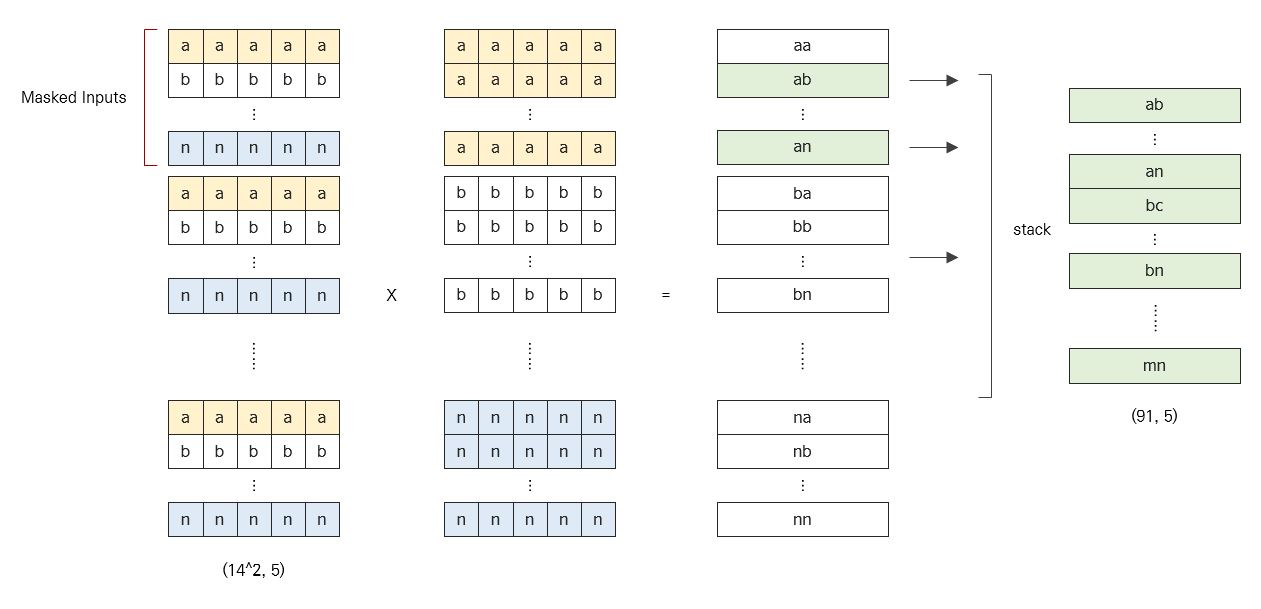
위 그림에서 14는 num_field의 예시이고, 5는 embedding_size의 예시이다. 가장 왼쪽에 있는 그림은 Embedding Layer를 통과한 Input 행렬을 그대로 num_field 수 만큼 쌓은 형태이이고, 그 오른쪽 그림은 똑같은 행들을 num_field 수만큼 쌓은 형태이다. 이렇게 쌓은 두 행렬 집단을 그대로 원소곱을 하게 되면 마치 조합을 구해서 곱을 한 것과 같은 형태가 나온다. 여기서 필요한 행들만 masking을 통해 취하면, 제일 오른쪽과 같은 결과물을 얻을 수 있다.
이를 코드를 구현한 것이 아래이다. tf.tile, tf.expand_dims 함수를 잘 이용하면 이 Trick을 코드로 구현할 수 있다. 직접 해보길 바란다.
class Pairwise_Interaction_Layer(tf.keras.layers.Layer):
def __init__(self, num_field, num_feature, embedding_size):
super(Pairwise_Interaction_Layer, self).__init__()
self.embedding_size = embedding_size # k: 임베딩 벡터의 차원(크기)
self.num_field = num_field # m: 인코딩 이전 feature 수
self.num_feature = num_feature # p: 인코딩 이후 feature 수, m <= p
masks = tf.convert_to_tensor(config.MASKS) # (num_field**2)
masks = tf.expand_dims(masks, -1) # (num_field**2, 1)
masks = tf.tile(masks, [1, embedding_size]) # (num_field**2, embedding_size)
self.masks = tf.expand_dims(masks, 0) # (1, num_field**2, embedding_size)
def call(self, inputs):
batch_size = inputs.shape[0]
# a, b shape: (batch_size, num_field^2, embedding_size)
a = tf.expand_dims(inputs, 2)
a = tf.tile(a, [1, 1, self.num_field, 1])
a = tf.reshape(a, [batch_size, self.num_field**2, self.embedding_size])
b = tf.tile(inputs, [1, self.num_field, 1])
# ab, mask_tensor: (batch_size, num_field^2, embedding_size)
ab = tf.multiply(a, b)
mask_tensor = tf.tile(self.masks, [batch_size, 1, 1])
# pairwise_interactions: (batch_size, num_field C 2, embedding_size)
pairwise_interactions = tf.reshape(tf.boolean_mask(ab, mask_tensor),
[batch_size, -1, self.embedding_size])
return pairwise_interactions
config.MASKS는 아래와 같이 구현되어 있다.
MASKS = []
for i in range(NUM_FIELD):
flag = 1 + i
MASKS.extend([False]*(flag))
MASKS.extend([True]*(NUM_FIELD - flag))
다음으로는 마지막 Attention Pooling Layer이다. 설명할 것이 많지 않은 간단한 구조이다.
class Attention_Pooling_Layer(tf.keras.layers.Layer):
def __init__(self, embedding_size, hidden_size):
super(Attention_Pooling_Layer, self).__init__()
self.embedding_size = embedding_size # k: 임베딩 벡터의 차원(크기)
# Parameters
self.h = tf.Variable(tf.random.normal(shape=(1, hidden_size),
mean=0.0, stddev=0.1), name='h')
self.W = tf.Variable(tf.random.normal(shape=(hidden_size, embedding_size),
mean=0.0, stddev=0.1), name='W_attention')
self.b = tf.Variable(tf.zeros(shape=(hidden_size, 1)))
def call(self, inputs):
# 조합 수 = combinations(num_feauture, 2)
# inputs: (None, 조합 수, embedding_size)
# --> (전치 후) (None, embedding_size, 조합 수)
inputs = tf.transpose(inputs, [0, 2, 1])
# e: (None, 조합 수, 1)
e = tf.matmul(self.h, tf.nn.relu(tf.matmul(self.W, inputs) + self.b))
e = tf.transpose(e, [0, 2, 1])
# Attention Score 산출
attention_score = tf.nn.softmax(e)
return attention_score
2.3. Model Build
위에서 설명한 모든 Layer들을 이어 붙이면 AFM 모델이 완성된다.
# Model 정의
from layers import *
tf.keras.backend.set_floatx('float32')
class AFM(tf.keras.Model):
def __init__(self, num_field, num_feature, num_cont, embedding_size, hidden_size):
super(AFM, self).__init__()
self.embedding_size = embedding_size # k: 임베딩 벡터의 차원(크기)
self.num_field = num_field # m: 인코딩 이전 feature 수
self.num_feature = num_feature # p: 인코딩 이후 feature 수, m <= p
self.num_cont = num_cont # 연속형 field 수
self.hidden_size = hidden_size # Attention Pooling Layer Hidden Unit 수
self.embedding_layer = Embedding_layer(num_field, num_feature,
num_cont, embedding_size)
self.pairwise_interaction_layer = Pairwise_Interaction_Layer(
num_field, num_feature, embedding_size)
self.attention_pooling_layer = Attention_Pooling_Layer(embedding_size, hidden_size)
# Parameters
self.w_0 = tf.Variable(tf.zeros([1]))
self.w = tf.Variable(tf.zeros([num_feature]))
self.p = tf.Variable(tf.random.normal(shape=(embedding_size, 1),
mean=0.0, stddev=0.1))
self.dropout = tf.keras.layers.Dropout(rate=config.DROPOUT_RATE)
def __repr__(self):
return "AFM Model: embedding{}, hidden{}".format(self.embedding_size, self.hidden_size)
def call(self, inputs):
# 1) Linear Term: (None, )
linear_terms = self.w_0 + tf.reduce_sum(tf.multiply(self.w, inputs), 1)
# 2) Interaction Term
masked_inputs = self.embedding_layer(inputs)
pairwise_interactions = self.pairwise_interaction_layer(masked_inputs)
# Dropout and Attention Score
pairwise_interactions = self.dropout(pairwise_interactions)
attention_score = self.attention_pooling_layer(pairwise_interactions)
# (None, 조합 수, embedding_size)
attention_interactions = tf.multiply(pairwise_interactions, attention_score)
# (None, embedding_size)
final_interactions = tf.reduce_sum(attention_interactions, 1)
# 3) Final: (None, )
y_pred = linear_terms + tf.squeeze(tf.matmul(final_interactions, self.p), 1)
y_pred = tf.nn.sigmoid(y_pred)
return y_pred
2.4. 코드 전문
코드의 전문은 깃헙에서 확인할 수 있다.

