목차

• Heterogeneous Graph Transformer 설명
  • 1. Background
  • 2. Heterogenous Graph Mining
  • 3. Heterogenous Graph Transformer
    • 3.1. Heterogenous Message Passing & Aggregation
      • Step1: Heterogenous Mutual Attention
      • Step2: Heterogenous Message Passing
      • Step3: Target-specific Aggregation
    • 3.2. Additional setting
      • 1번째 장치: Relative Temporal Encoding
      • 2번째 장치: HGSampling
      • 3번째 장치: Inductive Timestamp Assignmant
  • 4. Evaluation and Conclusion

이번 글에서는 HGT란 알고리즘에 대해 다뤄보겠다. 상세한 내용은 논문 원본을 참고하길 바라며, 본 글에서는 핵심적인 부분에 대해 요약 정리하도록 할 것이다. 저자의 코드는 Github에서 확인할 수 있다.

Heterogeneous Graph Transformer 설명

1. Background

기존의 많은 GNN이 Homogenous Graph에만 집중된 것에 반해, HGT는 여러 node type, edge type을 가진 Heterogenous Graph 데이터에 대해 적합한 알고리즘으로 제안되었다.

Heterogenous Graph에 대한 접근법은 여러 가지가 있지만 대표적으로 meta-path를 이용한 방법과 GNN을 이용한 방법이 존재한다. 그런데 이러한 방법에는 몇 가지 결점이 존재한다.

• heterogenous graph의 각 type에 맞는 meta-path design을 하려면 구체적인 domain 지식이 필요하다.
• 다른 type의 node/edge가 같은 feature를 공유하거나, 혹은 아예 다른 feature를 갖는 경우 graph의 특징을 온전히 포착하기는 어렵다.
• 모든 graph의 동적 특성은 대부분 무시되고 있다.

HGT의 목표는 다음과 같다.

• Network dynamics는 포착하면서 각 node/edge-type에 적합한 representation 학습
• customized meta-path를 특별히 설계하지 않음
• Web-scale graph에 적합하도록 highly scalable할 것

2. Heterogenous Graph Mining

Heterogenous Graph의 정의에 대해 살펴보자.

각 집합은 node, edge, node type, edge type을 의미한다. 이 때 각 node $v \in \mathcal{V}$ 이고, 각 edge $e \in \mathcal{E}$ 이다. 그리고 다음과 같은 type mapping 함수가 존재한다.

본격적인 구조 설명에 앞서 몇 가지 개념들에 대해 짚고 넘어간다.

Meta Relation
edge $e = (s, t)$ 가 존재할 때, 각 node $s, t$ 는 물론 edge $e$ 도 각자의 type을 가질 것이다. 이 때 이들 관계의 meta relation은 아래와 같이 표현할 수 있다.

이는 기존의 여러 meta-path 방법론에서도 설명된 개념이다. 3개의 요소 모두가 같아야만 같은 관계로 인식된다. 그런데 HGT는 여기에서 시간의 개념을 추가한다.

Dynamic Heterogenous Graph
앞서 예시로 들었던 edge $e=(s, t)$ 에 timestamp $T$ 를 할당해보자. 이는 node $s$ 가 $T$ 시점에 node $t$ 와 연결되었음을 의미한다. 이러한 관계가 처음으로 나타났다면 $s$ 에게 $T$ 시점이 할당된다. 물론 node $s$ 가 여러 번 연결된다면 복수의 timestamp를 갖게 될 것이다.

이는 edge의 timestamp는 불변함을 의미한다. 당연하다. 예를 들어 어떤 논문이 WWW에 1994년에 등재되었다면, 이 때의 timestamp는 1994년인 것이다.

3. Heterogenous Graph Transformer

HGT의 목표는 source node로 부터 정보를 통합하여 target node $t$ 에 대한 contextualized representation을 얻는 것이다.

3.1. Heterogenous Message Passing & Aggregation

아래 그림은 전체적인 구조를 나타낸다. 총 $L$ 개의 Layer를 쌓는 방식으로 되어 있고, $H^l$ 은 $l$ 번째 HGT layer의 output이다.

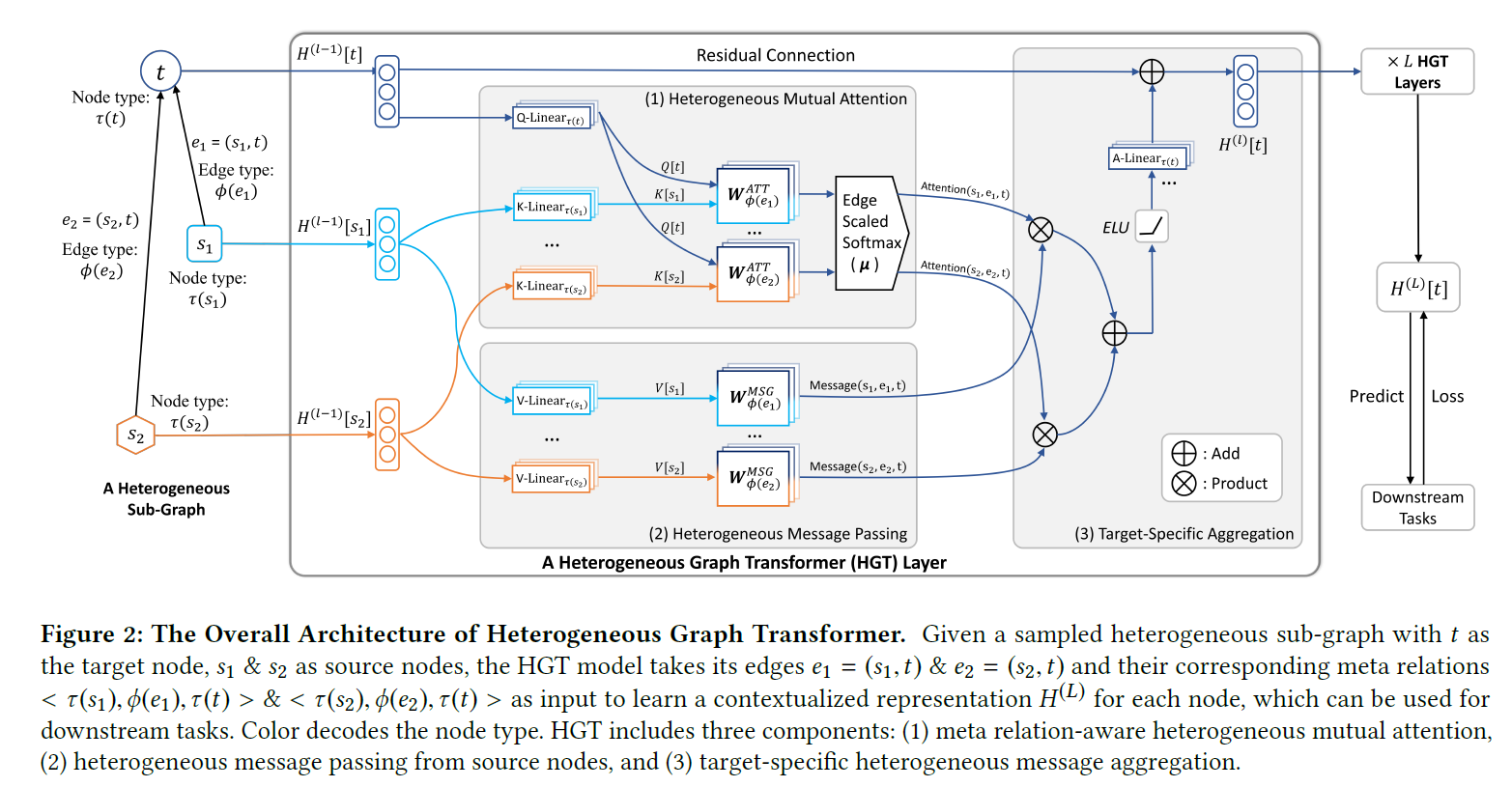
(1), (2), (3)으로 구분되어 있듯이 이 과정은 크게 3가지로 구분되며, 효과적인 학습을 위해 3가지의 추가적인 장치가 배치된다. 추가적인 장치는 3.2에서 설명하도록 하겠다.

Step1: Heterogenous Mutual Attention
Step2: Heterogenous Message Passingg
Step3: Target-specific Aggregation

일단 주어진 상황은 다음과 같다. 특정 target node $t$ 가 존재할 때, 2개의 source node $s_1, s_2$ 가 $e_1, e_2$ 라는 edge를 통해 target node와 관계를 맺고 있는 것이다. 이 때 node인 $t, s_1, s_2$ 의 경우 node feature 벡터를 갖는다. (node feature가 없으면 인위적으로 생성해야 한다.) 각 feature 벡터의 길이는 일단 $d$ 로 같다고 가정한다. 실제로는 최초의 Projection Layer에서 같은 길이로 통일되기 때문에 node type별로 다른 feature 길이를 가져도 무방하다. 어쨌든 지금은 $d$ 라는 길이로 통일되어 있다고 생각하자. 그렇다면 지금까지의 이야기로 2개의 meta relation이 존재하는 것이다.

1번째 meta relation을 기준으로 이야기를 이어나가 보겠다. Step1, 2에서 해야할 일은 source node $s_1$ 이 $e_1$ 이라는 edge를 통해 target node $t$ 에 주는 영향력을 수식으로 나타내는 것이다. 이는 Multi-head Attention으로 구현되는데, 기존의 Vanilla Transformer를 사용하면 다른 source/target node, 여러 node type 모두 같은 feature distribution을 공유하게 되므로 이는 현재 상황에 적합한 세팅은 아니다.

Step1: Heterogenous Mutual Attention

이러한 단점을 보완하기 위해 Heterogenous Mutual Attention 메커니즘이 도입된다. 이 메커니즘은 Multi-head Attention의 핵심 구조는 그대로 따르지만 몇 가지 차이점이 있다. 먼저 target node 벡터와 source node 벡터는 각각 Query 벡터, Key 벡터로 매핑되는데 이 때 각각의 node type에 따라 projection weight parameter가 다르다. 즉 만약 node type이 10개 있다고 하면, Query 벡터를 만들기 위한 weight matrix는 기본적으로 10 종류가 있는 것이다. (후에 여기에 attention head 수를 곱해야 한다.)

여기가 끝이 아니다. edge type도 weight parameter를 구분한다. $W_{\phi(e)}^{ATT}$ 가 edge type에 dependent한 weight으로 Query 벡터와 Key 벡터의 유사도를 반영한다. 지금까지 설명한 것을 식으로 보자.

2번째 식을 $h$ 개 만들고 이를 concat한 뒤 target별로 softmax 함수를 적용한 것이 최종 결과이다. 즉 2번째 식은 head 1개에 대한 결과물을 의미한다.

식의 좌측이 앞서 설명한 부분으로 아래와 같이 좀 더 세부적으로 표현할 수 있다.

위는 node type에 따라 weight를 구분하는 projection layer다. 이전 layer의 결과물을 받아 linear layer 하나를 통과시켜 Query/Key 벡터를 얻는다. 최종적으로 $h$ 개의 attention head를 얻기 때문에 Query/Key 벡터는 $\mathcal{R}^d \rightarrow \mathcal{R}^{\frac{d}{h}}$ 로 바뀐다. $W_{\phi(e)}^{ATT}$ 는 $\mathcal{R}^{\frac{d}{h}, \frac{d}{h}}$ 의 형상을 갖는다.

지금까지의 과정을 종합해보면, 이 Heterogenous Mutual Attention 메커니즘이 여러 종류의 semantic relation을 충분히 포착할 수 있을 구조를 갖고 있다는 느낌이 들기 시작한다. 그 효용성에 대해서는 검증해보아야겠지만 일단 장치는 마련해둔 셈이다.

2번째 식에서 우측을 보면 아래와 같은 수식이 있다.

논문에서는 이 식을 prior tensor라고 지칭하고 있다. 생각해보면, 모든 node/edge type이 같은 영향력을 지니지는 않을 것이다. 즉 데이터 전반을 볼 때 특정 node/edge type이 더 강한 영향력을 지닐 수도 있는 것이다. 이를 반영하기 위해 만들어진 tensor라고 생각하면 된다. 이 tensor를 통해 attention에 대해 adaptive scaling을 수행한다.

코드를 잠시 보고 지나가겠다.

self.relation_pri = nn.Parameter(torch.ones(num_relations, self.n_heads))

논문 원본에는 모든 node/edge type에 따른 prior를 부여하였는데, 저자의 코드는 이를 좀 단순화하여 나타냈다. 만약 원본 코드를 사용할 계획이라면 상황에 따라 수정을 가할 수도 있을 것이다. 만약 수정을 원한다면 아래 부분에서 행렬 곱 연산을 수행한 후에 합 연산을 수행하는 형태로 바꿔줘야 한다.

res_att[idx] = (q_mat * k_mat).sum(dim=-1) * self.relation_pri[relation_type] / self.sqrt_dk

코드에 대한 자세한 리뷰는 추후에 업로드하도록 하겠다.

앞서 언급하였듯이 최종 단계에서의 softmax는 target node를 기준으로 이루어지기 때문에 현재와 같이 1번째 meta relation 만을 기준으로 연산을 수행한다면 각각의 head에 대해 softmax가 아닌 sigmoid 함수가 적용되게 될 것이다. 2번째 meta relation까지 한번에 계산했다면 2개의 target node에 대해 softmax 함수가 적용되어 결과물로 길이 $h$ 의 벡터가 2개 주어질 것이다.

이를 그림으로 나타내면 아래와 같다.

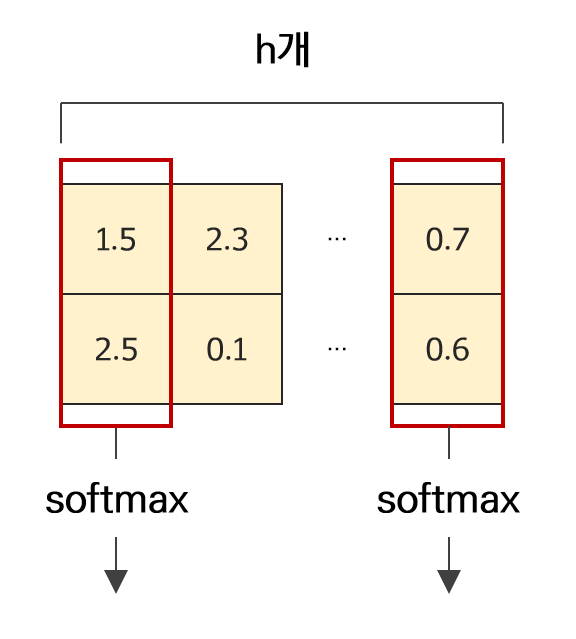
Step2: Heterogenous Message Passing

이전 섹션에서 주어진 edge type 하에서 source node와 target node 사이의 유사성에 대해 계산하였다면, 본 섹션에서는 이제 source node로부터 수집한 정보를 target node로 전달할 차례이다. 이 때 일반적인 honogenous graph network에서는 이러한 정보가 동일한 파라미터를 통해 업데이트되었겠지만, Heterogenous Message Passing 메커니즘에서는 source node type과 edge type에 따라 다른 파라미터를 지정하여 진행하게 된다.

Mutual Attention 과정을 보았기 때문에 특별히 어려울 것은 없다. 다만 위 수식에서의 M은 Transformer의 V 부분을 의미하고 실제 저자의 코드에서는 V-Linear라고 표기되어 있음에 유의하자.

Step3: Target-specific Aggregation

이전 2개 과정을 통해 attention score와 message를 수집/계산하였다. 지금부터는 이를 target node에 맞춰 통합하는 과정으로 이어진다.

위 meta relation 들에 대하여 attention score와 message를 모두 얻었다면 이 둘을 곱하여 updated vector를 얻을 차례이다.

이 과정을 거치면 다른 feature distribution을 갖는 source node의 이웃들이 target node $t$ 로 정보를 통합하게 될 것이다. 이제 target node $t$ 의 updated vector를 맞는 type에 따라 다시 한 번 linear layer를 통과시킨다. 그리고 이전 layer의 output을 직접적으로 더해주어 residual connection 또한 추가해준다.

이와 같은 과정을 $L$ 번 반복해주면 바로 그 결과물이 target node의 contextualized representaion이 되는 것이고, 이를 통해 node classification이나 link prediction과 같은 downstream task에 활용하면 된다.

정리를 좀 해보면, HGT는 분명 meta relation을 활용하여 각 type에 맞는 weight matrix를 따로 설정하고 이를 자연스럽게 통합하고 있다. 다만 이렇게 별개의 weight matrix를 모두 만들 경우 분명 model이 무거워지는 것은 사실이다. 따라서 실제 적용 시에는 이러한 부분에 대해 유의해야 할 것이다.

3.2. Additional setting

앞서 효과적인 학습을 위해 3가지의 추가적인 장치가 구현되어 있다고 언급한 바 있다. 이제 이 부분에 대해 살펴볼 것이다.

1번째 장치: Relative Temporal Encoding

RTE는 graph dynamic을 다루기 위해 도입된 개념이다. 시간적 정보를 활용하기 위해 시간대 별로 분리된 graph를 구성하는 이전의 방법은 여러 time slot간의 구조적인 연결성을 잃어버리기 때문에 효과적인 방법으로 보기 어렵다. dynamic graph를 모델링하는 것의 핵심은 바로 모든 node/edge가 다른 timestamp에서도 서로 상호작용할 수 있게 만들어주는 것이다.

이러한 철학은 Transformer의 positional encoding을 변형하여 구현된다.

source node $s$ 의 timestamp는 $T(s)$ 이고 target node $t$ 의 timestamp는 $T(t)$ 이다. 이 둘 사이의 relative time gap은 $\Delta T(t, s) = T(t) - T(s)$ 로 표현할 수 있고, relative temporal encoding을 $RTE(\Delta T(t, s))$ 라고 표기한다.

학습 데이터셋이 모든 time gap을 커버하는 것은 아니기 때문에 RTE는 본 적 없는 시간에 대해서도 일반화할 수 있어야 한다. 이를 위해 논문에서는 sinusoid 함수를 basis로 놓고 학습 가능한 projection layer를 하나 더 둔다.

최종적으로 target node $t$ 에 대한 temporal encoding은 source node $s$ 의 representation에 더해진다.

이 과정을 그림으로 나타내면 아래와 같다.

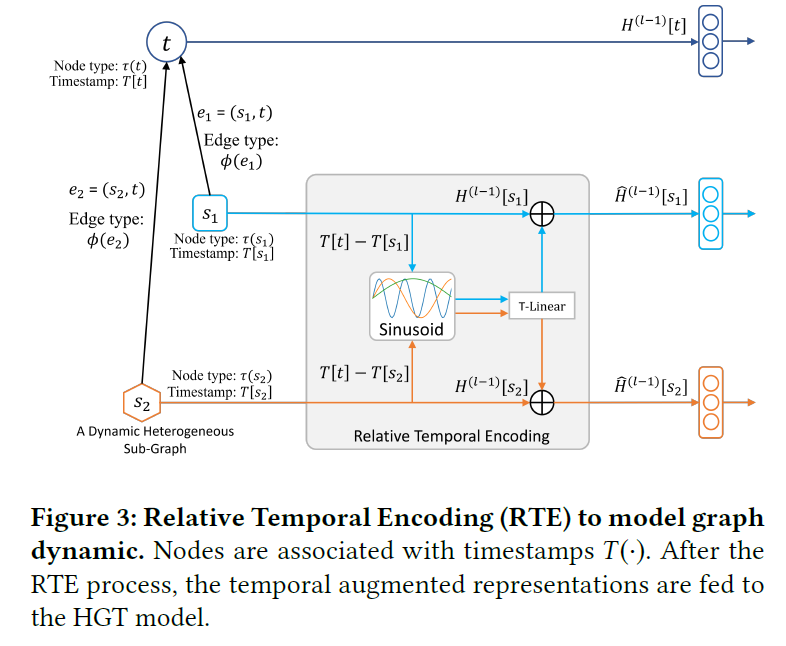
코드로 구현하면 아래와 같다.

class RelTemporalEncoding(nn.Module):
    # Implement the Temporal Encoding (Sinusoid) function.
    def __init__(self, n_hid, max_len=240):
        super(RelTemporalEncoding, self).__init__()
        position = torch.arange(0., max_len).unsqueeze(1)
        div_term = torch.exp(torch.arange(0, n_hid, 2) * -(math.log(10000.0) / n_hid))

        emb = nn.Embedding(max_len, n_hid)
        emb.weight.data[:, 0::2] = torch.sin(position * div_term) / math.sqrt(n_hid)
        emb.weight.data[:, 1::2] = torch.cos(position * div_term) / math.sqrt(n_hid)
        emb.requires_grad = False

        self.emb = emb
        self.lin = nn.Linear(n_hid, n_hid)
    def forward(self, x, t):
        return x + self.lin(self.emb(t))

edge_time이 주어지고, meta relation이 주어졌을 때 temporal encoding이 source node $s$ 의 representation에 더해지는 과정은 아래와 같이 구현된다.

rte = RelTemporalEncoding(n_hid=10)

source_node_vec = rte(source_node_vec, edge_time[idx])

2번째 장치: HGSampling

지금부터 설명할 2개의 방법론은 모두 scalibility를 향상시키기 위해 도입된 장치들이다.

작은 graph가 아니라면 full-batch GNN 학습은 현실적으로 힘든 경우가 많다. 그리고 속도와 효율을 중시하는 실제 서비스에 적용하기에는 부담스러운 측면도 있다. 이를 위해 sampling 방법이 많이 도입 되었는데, 이를 node-level로 추출할 수도 있고, grpah-level로 추출할 수도 있다. 이와 관련된 연구는 매우 많지만 node-level sampling을 적용한 알고리즘으로는 GraphSAGE, PinSAGE가 있고, IGMC, GraphSAINT는 graph-level sampling을 적용하였다.

그런데 앞서 소개한 방법들을 그대로 heterogenous graph에 적용할 경우, 만약 node type별 분포가 크게 다를 경우 상당히 불균형적이고 왜곡된 subgraph가 추출될 수 있다. 따라서 이를 위해 HGSampling이라는 방법이 제안된다.

HGSampling은 각 node/edge type에 속하는 수를 유사하게 맞춰주면서 정보 손실을 최소화하고 sample variance를 줄이기 위해 추출된 subgraph를 dense하게 유지할 수 있는 알고리즘이다.

아래 도식에서 HGSampling의 수행 과정을 살펴볼 수 있다. 기본적으로 각 node type $\tau{r}$ 에 대해 budget 딕셔너리 $B[\tau{r}]$ 를 만들어준다. 그리고 중요도 기반의 sampling을 사용하여 node type 별로 같은 수의 node를 추출해준다.

node $t$ 가 이미 추출되었다고 할 때, 이 node의 직접적인 이웃들을 모두 상응하는 budget에 추가해준다. 추가하는 방식은 아래와 같다.

그리고 이 이웃들에게는 node $t$ 의 normalized degree를 더해준다. 이 값은 추후에 sampling 확률을 계산하기 위해 사용된다. 이러한 normalization은 high-degree node에 의해 크게 좌지우지 되는 sampling 방식을 피하면서도, 이웃들에 대한 각 sampled node의 random walk 확률을 모으는 것과 같은 효과를 지닌다.

budget이 업데이트된 이후, 알고리즘1의 line9에서 각 budget 속에 있는 각 node $s$ 의 cumulative normalized degree를 계산한다. 이러한 sampling probability는 sampling variance를 감소시키는 효과를 지닌다.

이후 계산된 확률에 기반하여 type $\tau$ 의 $n$ 개의 node를 추출하고 이를 output node set에 추가하고, 이웃목록을 budget에 업데이트한다. 추출된 node는 budget에서 제거된다.

최종적으로 우리는 이렇게 sampled된 node에 기반하여 adjacency matrix를 다시 생성한다.

위와 같은 과정으로 생성한 subgraph는 node type별로 유사한 수의 node를 갖게 되고, sampling variance를 감소시킬 수 있을만큼 충분히 dense하다. 따라서 이를 활용하여 web-scale heterogenous graph를 효과적으로 학습할 수 있다.

그림으로 표현하면 아래와 같다.

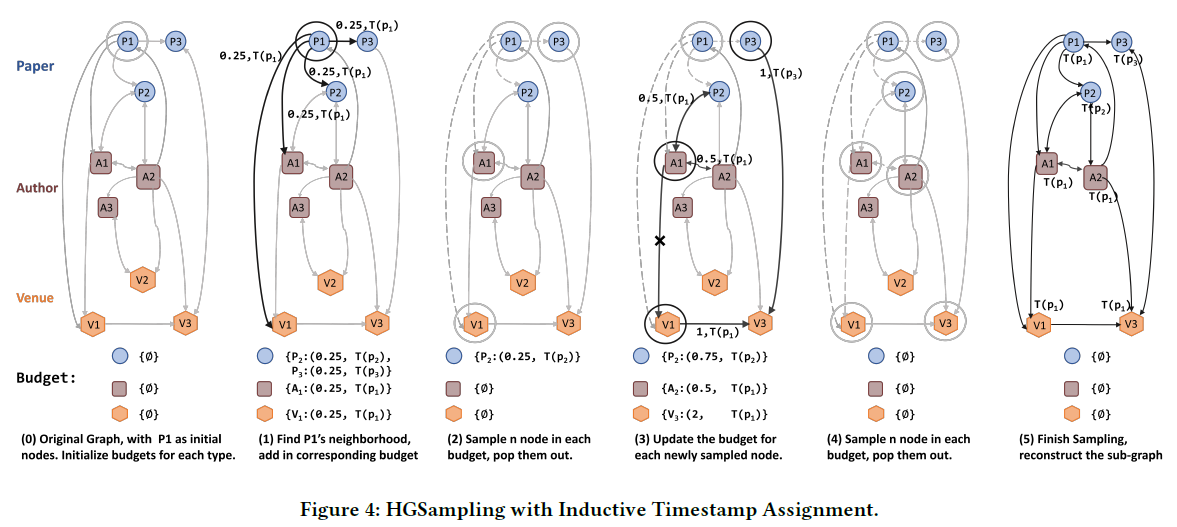
3번째 장치: Inductive Timestamp Assignmant

지금까지 우리는 각 node $t$가 timestamp $T(t)$ 에 assign되었다고 가정했는데 실 세계의 heterogenous graph에서 많은 node들은 고정된 시간으로 묶여있지 않다. 따라서 그러한 node에게는 다른 timestamp 들을 할당해주어야 하는데, 이러한 node를 plain nodes라고 한다.

또한 명시적인 timestamp를 갖고 있는 node들이 있는데 이들을 event nodes라고 한다. 본 논문에서는 event node의 timestamp에 기반하여 plain node의 timestamp를 assign하는 inductive timestamp assignment 알고리즘을 제안한다. plain node는 event node로 부터 timestamp를 상속받게 된다.

4. Evaluation and Conclusion