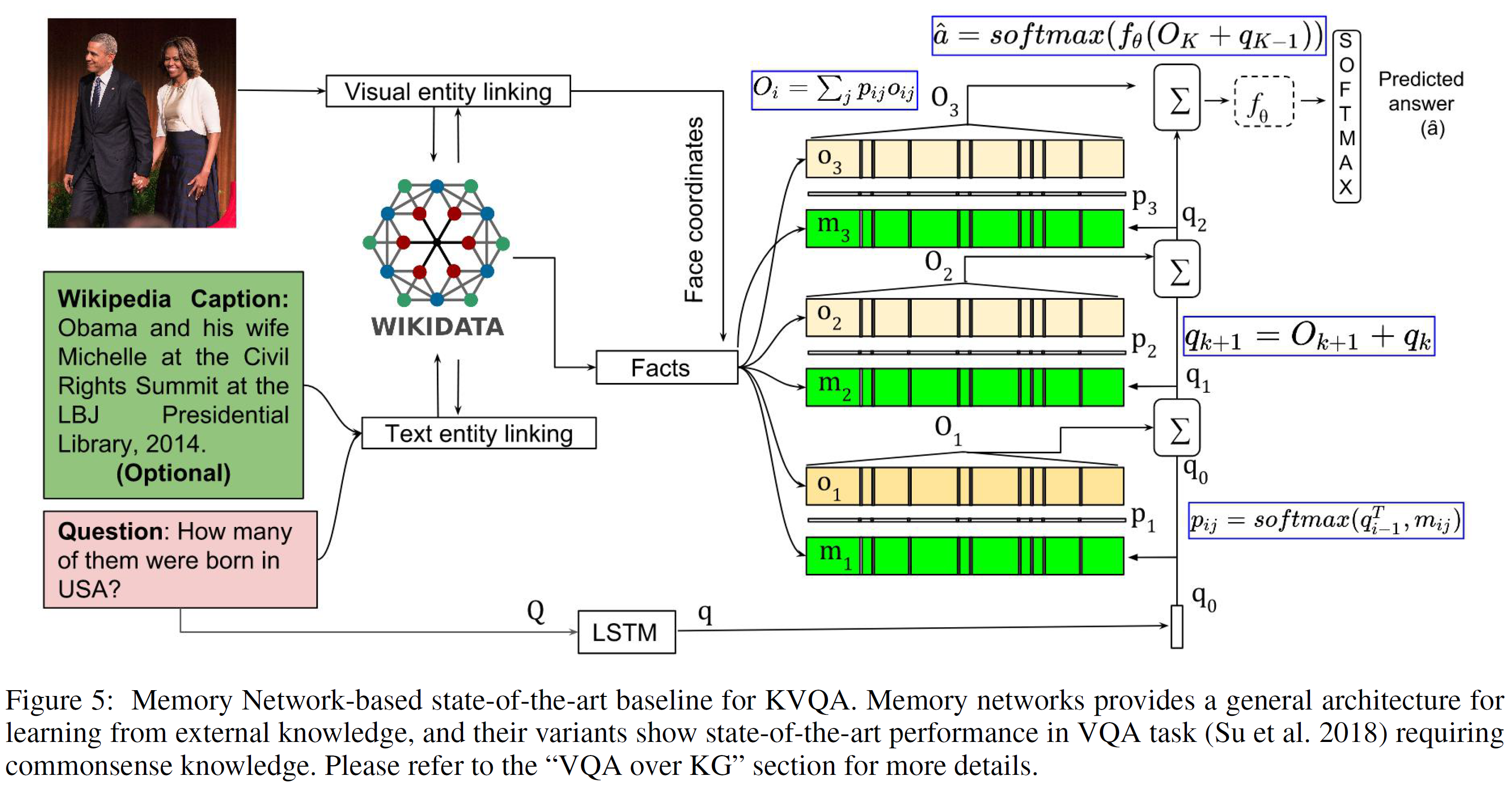
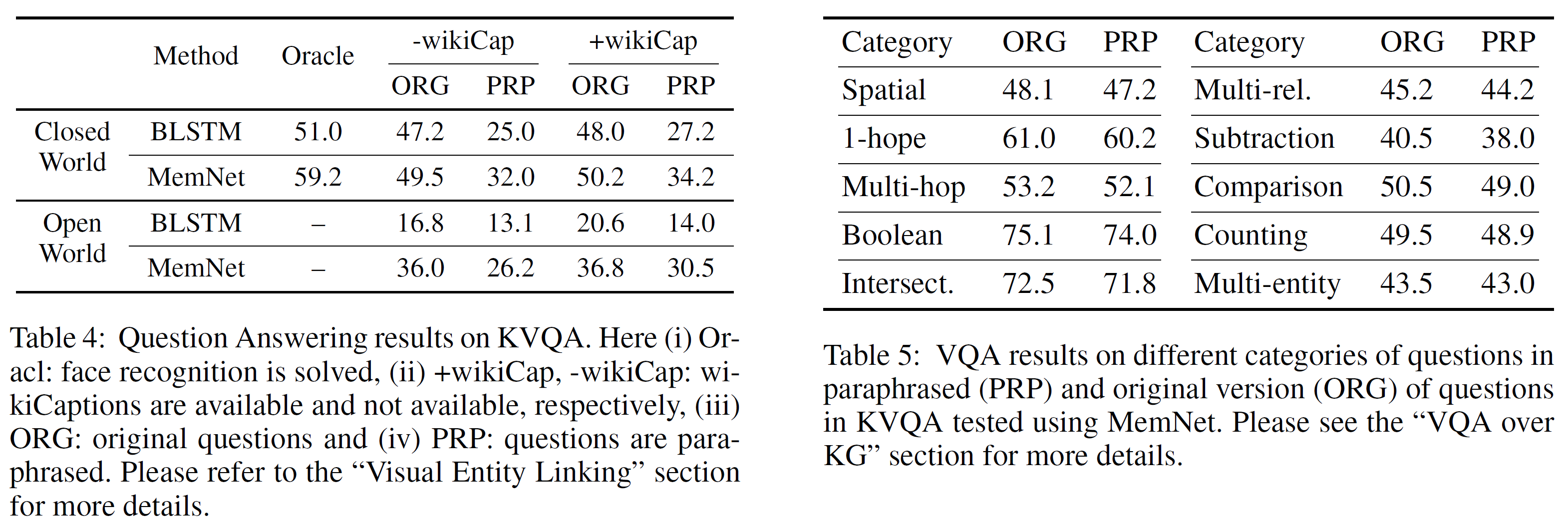
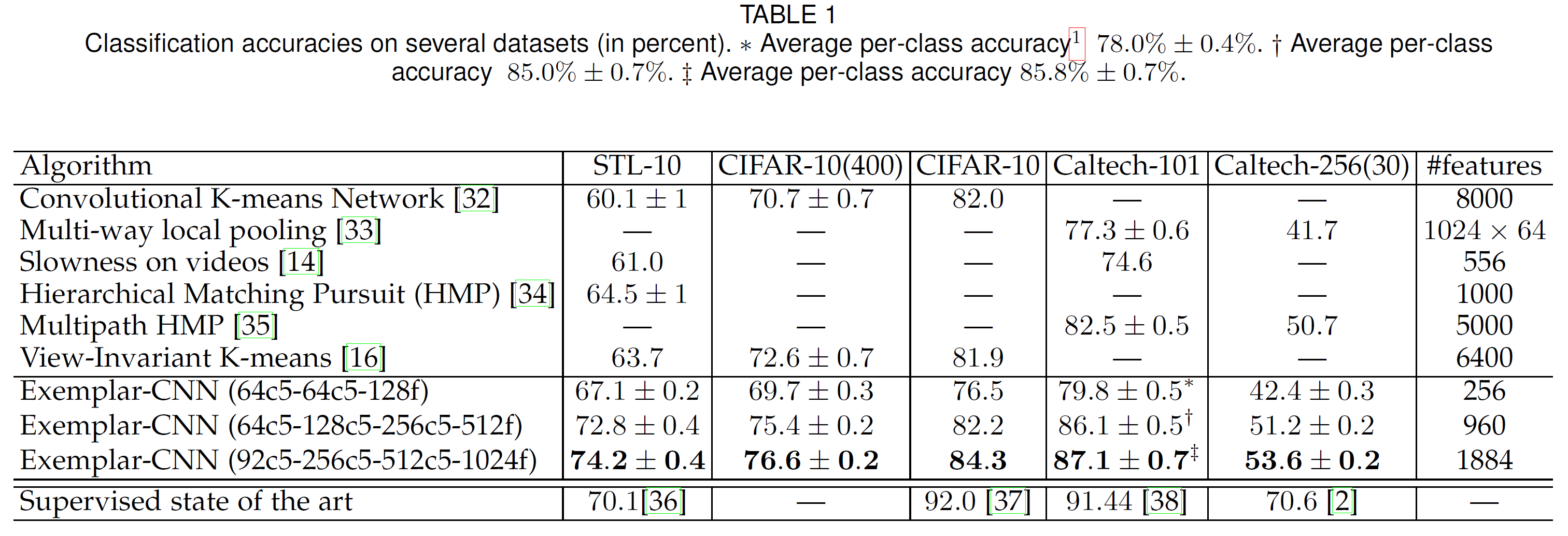
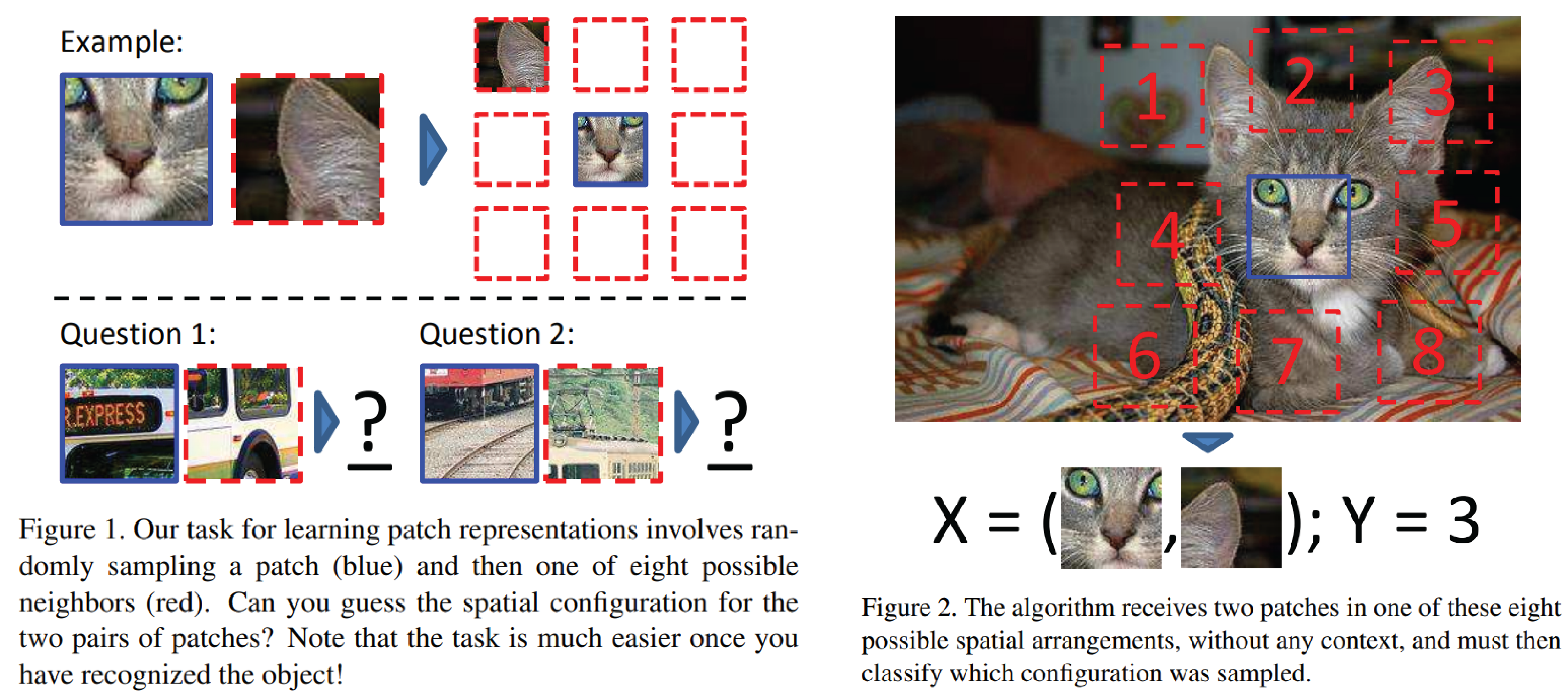
Graph Convolutional Matrix Completion (GCMC) 설명
06 Dec 2020 | Machine_Learning Recommendation System Paper_Review본 글은 2017년에 발표된 Graph Convolutional Matrix Completion에 대한 리뷰를 담은 글이다. Graph Neural Network에 대해서는 최근 수 년간 여러 연구가 이루어져 왔으며, 이 방법론은 다양한 분야에서 기존과는 사뭇 다른 새로운 해결 방안에 대해 제시하고 있다.
본 논문은 이러한 Graph 구조의 방법론을 추천 시스템, 그 중에서도 Matrix Factorization에 투영시킨 과정에 대해 설명하고 있다. 비록 적용에 있어 일부 한계점이 존재하기도 하지만, 추가적인 개선이 이루어진다면 여러 추천 시스템에서 참고할만한 중요한 인사이트들을 담고 있다고 할 수 있다. 먼저 논문 리뷰를 진행해보자.
1. Introduction
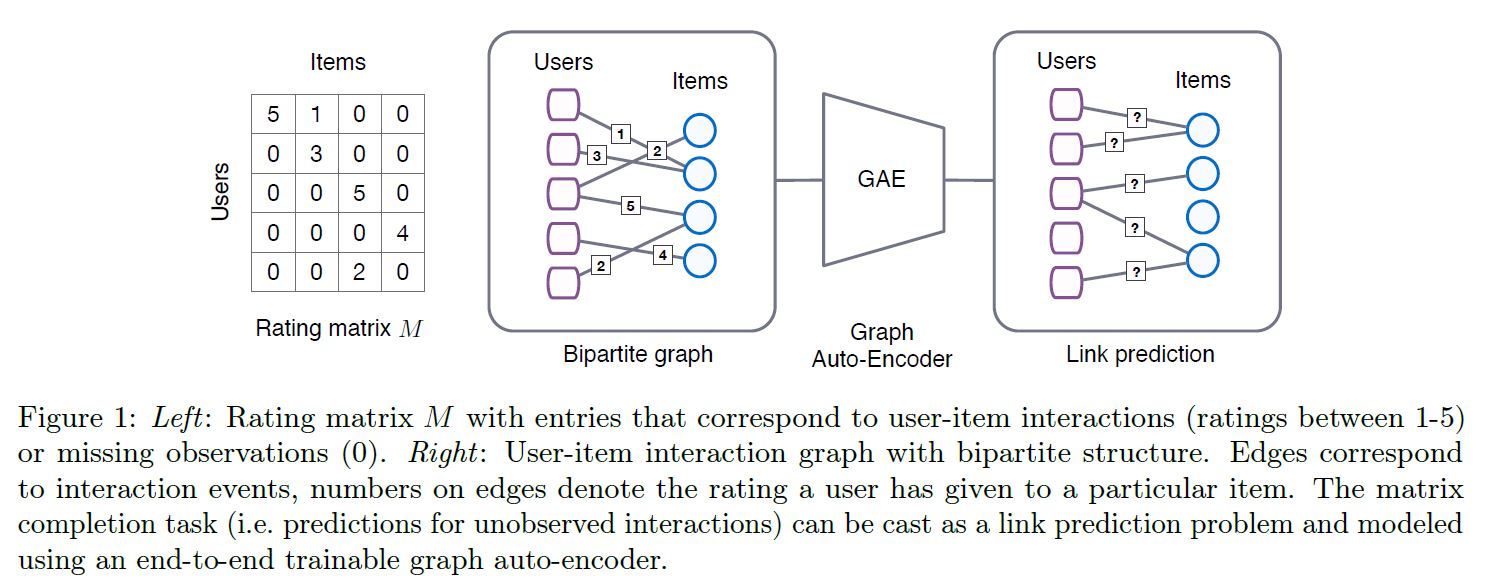
본 논문에서 우리는 Matrix Completion을 Graph에서의 Link 예측 문제라고 바라보고 있다. Collaborative Filtering에서의 상호작용 데이터는 Link로 표현되는 평점/구매 기록 그리고 User와 Item Node 사이의 Bipartite Graph (이분 그래프)로 표현된다. 컨텐츠 정보는 Node Feature로서 표현될 수 있다. 이제 평점을 예측하는 문제는 이분 User-Item Graph에서 라벨이 존재하는 Link를 예측하는 문제로 귀결된다.
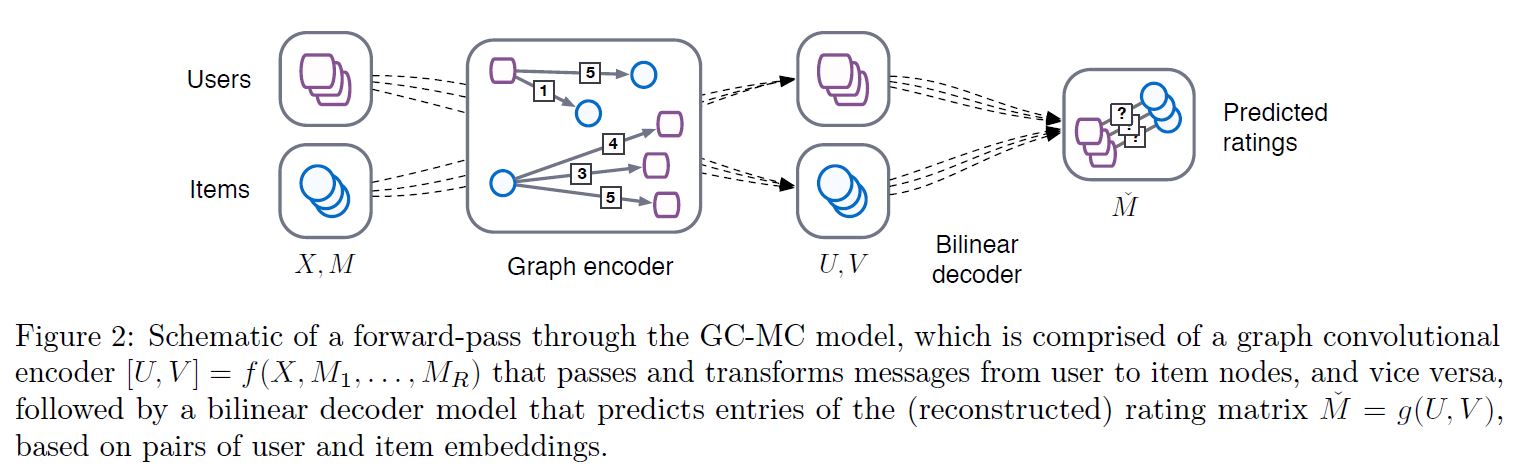
본 논문에서는 Graph에 대한 최근 딥러닝 발전 과정 속에서 설계한, Matrix Completion을 위한 Graph-based Auto-encoder 프레임워크인 Graph Convolutional Matrix Completion: GCMC를 제안한다. 이 때 Auto-encoder는 User와 Item Node의 잠재 벡터를 생성하는데, 이는 이분 상호작용 그래프에서느 Message Passing의 형태로 구현된다. 이 User와 Item (잠재) 표현은 Bilinear Decoder를 통해 평점 Link를 재구성(Reconstruct)하는데 이용된다.
추천 시스템에서 일반적으로 사업자는 특정 User에게 Item Pool에서 이 User에게 잘 어울린다고 생각하는 특정 Item를 골라서 제시하게 된다. 그런데 이러한 논리의 기저에는 유사한 User들은 유사한 Item들을 좋아할 것이라는, 그 User와 Item가 갖고 있는 근본적인 특성의 동질성이 취향에 발현될 것이라는 전제가 깔려있다. 이전의 Matrix Factorization 기반 방법론들은 User/Item Feature의 잠재벡터의 내적 계산을 통해 이러한 철학을 구현하였다.
본 논문에서 제시한 GCMC도 이러한 철학을 계승하고 있다. Graph 구조라고 해서 이 틀을 벗어나지는 않는 것이다. 가장 큰 차이는 바로 위 단락에서 언급한 Message Passing이 될 것인데, 이에 대해서는 추후에 자세히 설명할 것이다.
Matrix Completion 문제를 이분 그래프에서의 Link 예측 문제로 형상화하는 것은 추천 그래프가 구조화된 외부 정보(예: Social Network)를 동반할 때 더욱 빛을 발하게 된다. 이렇게 외부 정보를 추가하는 것은 Cold Start 문제를 완화하는데 도움을 준다.
2. Matrix Completion as Link Prediction in Bipartite Graphs
평점 행렬 $M$ 은 $N_u, N_v$ 의 크기를 가졌고, 행과 열의 수는 각각 User/Item의 수를 의미한다. 평점 행렬의 원소인 $M_{ij}$ 는 관측된 평점 값을 의미하는데, 이 값은 이산적인 (예: 1 ~ 5점) 값이고 미관측된 값은 0으로 처리한다. 최종 목적은 관측되지 않은 값을 예측하는 것이다.
Graph Network의 핵심 중 하나는 이러한 상호작용 데이터를 Undirected Graph (비방향성 그래프)로 표현한다는 것인데, 기호로 나타내자면 아래와 같다.
[G = (\mathcal{W}, \mathcal{E}, \mathcal{R}),]
[\mathcal{W} = \mathcal{U} \cup \mathcal{V},]
[(u_i, r, v_j) \in \mathcal{E},]
[r \in [1, …, R] = \mathcal{R}]
$\mathcal{W}, \mathcal{E}, \mathcal{R}$ 은 차례 대로, User/Item 집합, Edge 집합, Rating 집합을 의미한다. 즉, Graph라는 존재는 이와 같이 Node, Edge, Link로 이루어져 있다는 것을 의미한다.
2.1. Graph Auto-encoders
Graph Auto-encoder는 크게 2가지로 구성된다. 첫 번째는 Graph Encoder 모델로, $Z=f(X, A)$ 라고 정의할 수 있겠다. 이 때 각각의 Shape은 아래와 같다.
| 행렬 | 역할 | Shape |
|---|---|---|
| $Z$ | Node Embedding Matrix | $N, E$ |
| $X$ | 원본 Feature Matrix | $N, D$ |
| $A$ | Graph Adjacency Matrix | $N, N$ |
$D$ 는 모든 변수의 개수를 의미하며, $N$ 은 $N_u + N_v$ 를 의미한다.
두 번째는 Pairwise Decoder 모델로 $\hat{A} = g(Z) $ 로 정의할 수 있으며 Node Embedding 쌍 $(z_i, z_j)$ 를 Input으로 받아 Adjacency Matrix의 원소인 $\hat{A}_{ij}$ 를 예측하는 역할을 수행하게 된다.
$X$ 는 원본 Feature를 의미하고 이 행렬의 Shape은 $(N=N_u + N_v, D)$ 이다. 한 가지 궁금할 수 있는 부분은 이와 같은 표기에서는 User Feature의 변수의 수와 Item Feature의 변수의 수가 $D$ 로 동일한 것처럼 보이는데, 다음 Chapter를 보면 그렇게 만들 필요는 없다고 설명이 나온다. 처음부터 설명해주는 친절함은 조금 부족했던 것 같다. 어찌 되었든 여기에서의 $D$ 는 편의를 위해 통일 된 것으로 생각하면 좋을 것 같다.
$A$ 는 Adjacency Matrix (인접 행렬)를 의미하는데, 평점 데이터를 기반으로 설명하자면 이 $A$ 는 여러 조각으로 나뉠 수 있다. 즉, 1점의 평점을 준 Link를 모두 모은 인접 행렬을 $M_1$ 이라고 하고, R점의 평점을 준 Link를 모두 모은 인접 행렬을 $M_R$ 이라고 한다면, 우리는 Encoder 모델의 함수를 다음과 같이 달리 표현할 수 있을 것이다.
[Z = f(X, M_1, …, M_R)]
$Z$ 는 $[U, V]$ 로 표현되는데, User Embedding Matrix와 Item Embedding Matrix를 쌓아놓은 형태이다.
최종적으로 해결해야 하는 문제는 예상하는 그대로이다. Decoder $g(U, V)$ 는 $\hat{M}$ 이라는 평점에 대한 예측 값을 생성하게 되고, 이 행렬의 Shape은 당연히 기존 $M$ 과 동일한 $(N_u, N_v)$ 이다.
예측 행렬 $\hat{M}$ 과 관측된 Ground-Truth 행렬 $M$ 사이의 Reconstruction Error 를 줄이는 것이 본 모델의 목적이다.
2.2. Graph Convolutional Encoder
지금부터는 조금 더 진보된 형태의 Encoder 모델을 소개할 것이다. 이 모델은 Graph에서 location에 대한 효율적인 Weight Sharing을 특징으로 한다. 또한 이 모델은 각 평점 종류(Edge Type)에 대해 별도의 Processing Channel을 만든다. 즉 각각의 평점 종류(1점인지, 2점인지)에 따라 (형식은 같지만) 다른 처리 과정이 존재한다는 것이다.
Weight Sharing의 형식은 Graph 구조의 데이터에 직접적으로 작동하는 최근 CNN class에 영감을 받았는데, Graph Convolutional Layer가 Node의 1차 이웃만을 고려하여 지역 연산을 수행하면, 같은 Transformation이 Graph에 있는 모든 위치에서 수행된다는 것이다.
Graph 구조의 모델에 대해 처음 설명을 듣는다면 위 단락이 잘 이해가 되지 않을 수도 있다. 잠시 그림을 살펴보자.
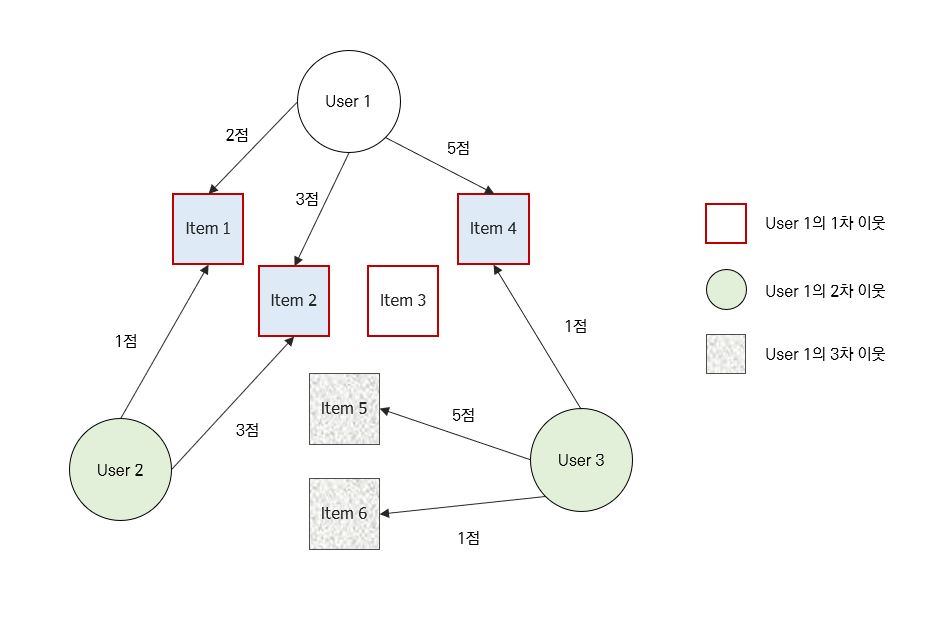
User 1이 존재한다. 이 User는 총 3개의 Item에 대해 평점을 남겼는데, 이렇게 User 1이 평점을 남긴 Item을 우리는 1차 이웃이라고 부른다. 즉 User 1과 직접적인 관계를 맺고 있는 Node라고 할 수 있다. 그렇다면 2차 이웃은 무엇일까? User 1이 평점을 남긴 1차 이웃 Item이 직접적인 관계를 맺고 있는 User 집합이라고 할 수 있는데, 이들은 그림 상에서 초록색 원형으로 표시되었다. 3차 이웃은 이제 감이 올 것이다. 2차 이웃 User가 직접적으로 관계를 맺고 있는 Item 집합을 의미한다. 이렇게 차수를 높여감에 따라 우리가 알고 싶은 User 1의 관계의 깊이가 점점 깊어진다는 것을 알 수 있다. 더 깊게 알고 싶을 수록 연산량이 늘어나는 것은 당연한 숙제가 될 것이다.
그렇다면 하나 더, 위 그림에서 추론할 수 있는 것은 무엇일까? 간단하게 말해서 User 1은 파란색 상자로 표현한 Item 1, 2, 4 중에서 Item 1과 2에 대해서는 아주 좋은 평점을 남기지는 않았는데, User 2도 이와 유사한 평점을 남겼다. 그렇다면, 오직 이 Graph만 보았을 때는 User 1과 User 2가 나름 취향이 비슷할 수도 있을 것이다. 이 때 평점이 몇 점인지도 중요하지만 어떤 Item에 대해 평점을 남겼는지도 중요하다. 그 User의 행동 반경을 정의하는 단서가 되기 때문이다. 반대로 User 3은 User 1이 좋아했던 Item 4에 대해 안 좋은 평점을 남겼다. 어쩌면 이 두 User는 상극일지도 모른다.
다시 논문으로 돌아오겠다.
Local Graph Convolution은 Vector 값으로 만들어진 Message가 Graph의 모든 Edge를 타고 전달 및 변형되는 일종의 Message Passing의 형태로 볼 수 있다. 본 논문에서는 각 평점에 따라 별도의 Transformation을 행했다. Item j가 User i에게 주는 Edge-type Specific Message는 아래와 같은 형식으로 표현할 수 있다.
[\mu_{j \rightarrow i, r} = \frac {1} {c_{ij}} W_r x_j]
여기서 $c_{ij}$ 는 정규화 상수인데, 만드는 방법에는 2가지가 있다. Left Normalization을 택할 경우, $\vert{\mathcal{N}_i}\vert$ 을, Symmetric Normaliztion을 선택할 경우 $\vert{\mathcal{N}_i}\vert \vert \mathcal{N_j} \vert$ 로 택할 수 있다.
$\mathcal{N_i}$ 는 Node $i$ 의 이웃들의 집합을 의미한다. 따라서 위 기호는 그 이웃 집합의 길이를 의미하게 될 것이다. $W_r$ 은 Edge-type Specific Parameter를 의미한다. 참고로 뒤에 나올 $W$ 행렬과는 별개의 것이다. 논문에서 다소 혼란스럽게 적어 놓았으니 구별하길 바란다. $x_j$ 는 Node $j$ 의 (Initial) Feature 벡터를 의미한다. 이 예시에서는 Node $j$ 가 Item 이지만, 반대의 경우도 당연히 성립한다.
이렇게 $r$ 이라는 평점에서 Node $j$ 에서 Node $i$ 로 향하는 Message Passing을 정의하는 단계가 끝나면, 이제 $r$ 이라는 평점 하의 모든 이웃 $\mathcal{N_{i, r}}$ 의 입수되는 모든 Message를 규합해야 한다. 그렇게 합쳐서 아래와 같이 하나의 벡터 표현을 만들게 된다. 아래 벡터를 반드는 층을 Graph Convolution Layer라고 명명하겠다.
[h_i = \sigma [accum (\Sigma_{j \in \mathcal{N_{i, 1}}} \mu_{j \rightarrow i, 1}, …, \Sigma_{j \in \mathcal{N_{i, R}}} \mu_{j \rightarrow i, R}) ]]
평점의 종류가 총 $R$ 개라고 할 때 위 식은 모든 평점의 종류에 대해 Node $i$ 의 1차 이웃에 속하는 Item Node $j$ 들에 대해 모든 Message를 합치는 과정으로 설명할 수 있다. 합친다는 것을 의미하는 $accum$은 Stacking으로 생각할 수도 있고, Sum으로 생각할 수도 있는데, Sum이 좀 더 구현하기 편리하니 Sum으로 일단 생각해두자.
이제 최종적으로 Node $i$ 의 Embedding Vector를 생성하면 된다. 아래와 같이 만들 수 있다. 최종 Embedding Vector를 생성하는 아래 층은 Dense Layer라고 명명하겠다.
[u_i = \sigma(W h_i)]
Item Embedding Vector $v_j$ 역시 같은 Paramter 행렬 $W$ 에 의해 유사한 방식으로 생성된다. 만약 User, Item에 대한 Side Information, 즉 별개의 Feature Vector를 사용할 경우 이 Parameter 행렬 $W$ 는 User, Item에 따라 별도로 구성해야 할 것이다. ( $W_{user}, W_{item}$ )
여러 층을 추가하여 더욱 깊은 모델을 만들 수도 있고, Message Passing 구성을 위와 같이 하는 대신 새로운 신경망이나 Attention 모델을 통해 구성하는 방안도 생각해볼 수 있다. 그러나 본 논문에 따르면 위와 같이 구성하는 방법이 가장 효율적인 것으로 나타났다.
논문에서는 이렇게 소 Chapter를 마무리하는데, 보충 설명을 하도록 하겠다.
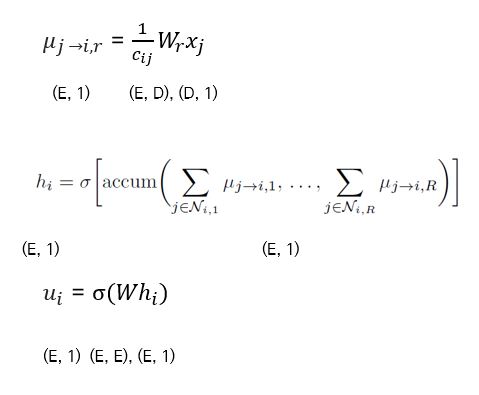
Message Passing 단위는 $\mu_{j \rightarrow i, r}$ 라는 벡터이다. 예시를 들어보자. 만약 평점이 1점, 2점 이렇게 2종류만 존재한다고 해보자. 그리고 User Node $i$ 가 1점을 준 Item Node는 $1, 2$ 이렇게 2가지가 있고, 2점을 준 Item Node는 $3$ 이렇게 1가지만 존재한다고 해보자.
그렇다면 User Node $i$ 의 이웃은 아래와 같이 구성할 수 있다.
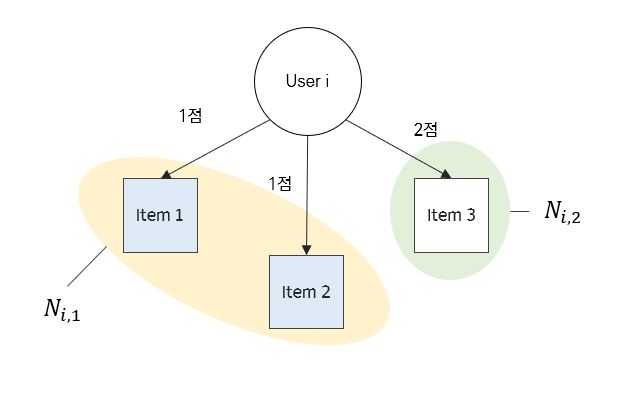
위 그림과 같은 구조에서 우리는 다음과 같은 Message Passing 벡터를 얻을 수 있다.
[\mu_{1 \rightarrow i, 1}, \mu_{2 \rightarrow i, 1}, \mu_{3 \rightarrow i, 2}]
위 벡터들의 의미는 무엇일까? 위 3개의 벡터 중 첫 번째를 예시로 들어보자. $1$ 이라는 Item Node가 User $i$ 에게 미치는 영향으로 해석가능하다. 이 때 어떻게 영향을 미칠 것인가에 대해서는 $W_1$ Parameter 행렬이 역할을 수행하게 될 것이다. 그런데 User $i$ 에게 1점의 관계를 맺고 있는 Item Node는 총 2개이다. 따라서 앞서 보았던 $c_{ij}$라는 정규화 상수를 통해 영향의 크기를 분산시켜주는 것이다.
이렇게 만들어진 단위 벡터들은 Graph Convolution Layer에서 합쳐지고 최종적으로 User, Item Embedding Vector을 형성하게 된다.
2.3. Bilinear Decoder
행렬 분해를 기반으로 하는 추천 시스템에 대해 한 번이라고 공부를 해보았다면, 이전 Chapter에서 언급한 임베딩 벡터의 의미를 알아챘을 것이다. 가장 Classic하게 평점을 예측하는 방법은 User 임베딩 벡터와 Item 임베딩 벡터를 바로 내적 계산하는 것이다.
[\hat{y}_{ij} = u_i \cdot v_j]
본 논문에서는 이러한 역할을 수행하기 위해 Bilinear Decoder라는 형태를 제안한다. 이 때 각 평점 종류 마다 다른 Parameter Update를 수행한다는 점에 주의하기 바란다. ( $Q_1, Q_2, …, Q_R$ )
$M$ 평점 행렬의 한 원소를 예측하는 과정은 아래와 같이 Softmax 함수에 의해 Bilinear 연산을 가능한 평점 종류에 대해 수행하고 이에 대한 확률 분포를 생성하는 방식으로 이루어진다.
[p(\hat{M}{ij}) = \frac {e^{u_i^T Q_r v_j}} {\Sigma{s \in R} e^{u_i^T Q_s v_j}}]
여기서 $Q_r$ 은 학습 가능한 Parameter 행렬로, $(E, E)$ 의 Shape을 지녔다. 물론 여기서 $E$ 는 Embedding 차원을 의미한다. 최종적으로 평점 예측은 아래 식으로 계산된다.
[\hat{M}{ij} = g(u_i, v_j) = \mathbf{E}{p(\hat{M}{ij = r}} [r] = \Sigma{r \in R} r * p(\hat{M}_{ij})]
식을 보면 평점의 종류에 따라 확률이 가중 평균됨을 알 수 있다.
2.4. Model Training
논문의 흥미로운 내용만큼이나 학습시키는 것은 상당히 까다롭다. 어떻게 진행되는지 알아보자.
Loss Function은 다음과 같은 Negative Log Likelihood로 설정된다.
[\mathcal{L} = \Sigma_{i, j; \Omega_{i,j} = 1} \Sigma_{r=1}^R I[r=M_{ij}] logp(\hat{M_{ij}} = r)]
여기서 $I$ 함수는 Indicator Function으로 $[]$ 안이 참일 때 1, 그렇지 않을 때 0의 값을 가지게 된다. 이는 일종의 Mask 역할을 수항하게 되는데, 왜냐하면 오직 평점 기록이 존재하는 Link에 대해서만 Loss를 계산한다는 의미가 되기 대문이다.
Node Dropout
관측되지 않은 평점에 대해 모델이 잘 일반화하기 위해서는 또다른 장치가 필요하다. 특정 Node에 대해 $p_{dropout}$ 확률로 밖으로 나가는 모든 Message를 무작위로 drop out하는 방식으로 학습하는 것을 Node Dropout이라고 한다.
Message는 Dropout 단계 이후에 Rescaled된다. Node Dropout을 적용한 결과 임베딩 결과물이 특정 User나 Item에 좀 더 독립적이 된 것을 확인할 수 있었다. 추가적으로 Hidden Layer Unit에 Regular Dropout 역시 적용하였다.
Mini-batching
미니 배치는 User-Item Pair 총합에서 오직 고정된 수의 Contribution 만을 추출하여 학습에 사용한다는 것을 의미한다. 이렇게 함으로써 현재 Batch에서 존재하지 않는, 각 평점 Class의 User/Item 행을 제거할 수 있다.
이러한 과정은 또한 효율적인 정규화의 수단으로 기능하며 모델을 학습시키기 위해 필요한 메모리 역시 경감시키는 효과를 발휘한다.
2.5. Vector Implementation
실제로 코드를 구현하여 모델을 학습할 때, 지금까지 설명한 것처럼 일일히 벡터를 하나씩 구하는 것은 정말 어리석은 행위일 것이다. 간단히 (사실 간단하지 않다) 행렬을 활용하여 수많은 연산을 좀 더 효율적으로 수행해보자.
User Feature와 Item Feature의 수가 $D$ 로 같다고 가정해보자. 이 때 Embedding 행렬은 아래와 같이 구할 수 있다.
[\begin{bmatrix} U \ V \end{bmatrix} = f(X, M_1, …, M_R) = \sigma( \begin{bmatrix} H_u \ H_v \end{bmatrix} W^T )]
[with \begin{bmatrix} H_u \ H_v \end{bmatrix} = \sigma(\Sigma_{r=1}^R D^{-1} \mathcal{M}_r X W_r^T),]
[\mathcal{M}_r = \begin{bmatrix} 0 M_r \ M_r^T 0 \end{bmatrix}]
이 때 $D$ 는 대각행렬이며, 대각원소 $D_{ii} = \vert \mathcal{N}_i \vert$ 을 의미한다.
각 행렬의 크기는 아래와 같다.
| 행렬 | 역할 | Shape |
|---|---|---|
| $\begin{bmatrix} U \ V \ \end{bmatrix}$ | Node Embedding Matrix | $N+M, E$ |
| $\begin{bmatrix} H_u \ H_v \ \end{bmatrix}$ | Hidden Matrix | $N+M, E$ |
| $W^T$ | Weight Matrix | $E, E$ |
| $D^{-1}$ | Normalization Matrix | $N+M, N+M$ |
| $A$ | Graph Adjacency Matrix | $N+M, N+M$ |
| $X$ | Feature Matrix | $N+M, D$ |
| $W_r^T$ | Edge-type Specific Weight Matrix | $D, E$ |
위와 같이 Encoder에서 벡터화한 방식을 그대로 Decoder에 적용하면 된다. 그리고 이러한 방식은 오직 관측된 원소를 평가할 때만 필요할 것이다.
2.6. Input Feature Representation and Side Information
컨텐츠 정보와 같이 각 Node에 대한 정보를 담고 있는 Feature는 Feature Matrix $X$ 라는 형태로 Input 레벨에서부터 투입될 수 있다. 그러나 만약 그러한 정보가 다른 User(Item)나 그들의 관심 사항을 제대로 구분할만한 충분한 정보를 갖고 있지 못하다면, 이 정보를 처음부터 Graph Convolutional Layer에 집어 넣으면 심각한 정보 병목현상이 발생할 수도 있다.
이러한 경우에는 Side Information으로 활용하는 방안을 생각해볼 수 있다. Node $i$ 에 대해 User/Item Feature Vector $x_i^f$ 를 만들고, 이를 Dense Hidden Layer에 독립적인 채널을 통해 직접적으로 투입하는 것이다.
[u_i = \sigma(W h_i + W_2^f f_i),]
[f_i = \sigma(W_1^f x_i^f + b)]
이 때 $W_1^f, W_2^f$ 는 학습 가능한 Weight 행렬이며, User Weight Matrix와 Item Weight Matrix는 구분된다. Graph Convolutional Layer를 위한 Node Feature를 담고 있는 Input Feature Matrix $X$ 는 Graph에 있는 모든 Node에 대한 고유한 One-Hot 벡터와 함께 Identity Matrix로 선택된다. 본 논문에서 사용된 데이터셋에 한해서는, User/Item Content 정보는 제한적인 크기를 갖고 있고 따라서 본 논문에서는 이들을 Side Information으로 이용하고자 한다.
Side Information은 꼭 Per-Node Feature 벡터의 형태일 필요는 없다. 사실 그래프 구조여도 되고, NLP 혹은 이미지 데이터일수도 있다. 물론 이 경우 위에서 보았던 식은 미분 가능한 적절한 다른 모듈로 대체되어야 할 것이다. RNN, CNN, GNN 같은 형태로 말이다.
논문에서의 이 부분은 기술적으로 다루기가 좀 어려운 부분이 있을 수는 있지만, 적절히 설계된다면 GCMC의 확장성에 관한 기술로 생각해볼 수 있으며 우리에게 주어진 Task에 유연하게 적용해볼 수도 있을 것이다.
2.7. Weight Sharing
One-Hot 벡터가 Input으로 주어지는 Collaborative Filtering 환경에서, Weight 행렬 $W_r$ 의 열은 특정 평점 값 $r$ 에 대해 독립적인 Node의 잠재 요인으로서의 역할을 갖게 된다. 참고로 $W_r$ 의 Shape은 $(E, D)$ 인데, 논문에서 말한 열의 의미를 생각해보면 Weight 행렬을 $W_r^T$ 로 전치하여 $(D, E)$ 의 Shape을 갖고 있다고 생각하고 바라보는 것이 좀 더 편할 것이다.
어쨌든 이 잠재 변수들은 Message Passing이라는 형태를 통해 연결된 User/Item Node로 전달된다. 그러나 모든 User와 Item이 각 평점 레벨에서 갖은 수의 평점을 갖고 있지는 않을 것이다. 이 말은, $W_r$의 특정 열은 다른 열들에 비해 상대적으로 덜 최적화되는 결과를 야기할 수도 있다는 것이다.
따라서 이러한 최적화 문제를 해결하기 위해 다른 평점 class $r$ 에 대해 $W_r$ 에 대한 어떤 형태의 Weight Sharing이 필요하다. 다음과 같은 식을 보자.
[W_r = \Sigma_{s=1}^r T_s]
본 논문에서는 위와 같은 방식의 Weight Sharing을 Ordinal Weight Sharing이라고 명명한다. 왜냐하면 높은 평점 레벨에는 더 많은 Weight 행렬이 들어가기 때문이다.
[W_1 = T_1]
[W_2 = T_1 + T_2]
[W_3 = T_1 + T_2 + T_3]
Pairwise Bilinear Decoder의 효과적인 정규화 수단으로 Basis Weight 행렬 $P_s$ 의 집합의 선형 결합의 형태로 Weight Sharing을 정의할 수 있겠다.
[Q_r = \Sigma_{s=1}^{n_b} a_{rs} P_s]
이 때 $n_b$ 는 기본 Basis Weight 행렬의 개수를 의미한다. $a_{rs}$ 는 학습 가능한 계수로, 각 Decoder Weight 행렬 $Q_r$ 의 선형 결합을 결정한다. 과적합을 피하고 파라미터의 수를 줄이기 위해 $n_b$ 는 평점 Class의 수보다는 작아야 할 것이다.
(중략)
5. Conclusions
Encoder는 Graph Convolutional Layer를 포함하는데, 이 layer는 User-Item 상호작용 Graph에서 오가는 Message 속에서 User/Item Embedding을 구성하게 된다. Bilinear Decoder와 결합하여 새 평점은 labeled edge의 형태로 예측되게 된다.
본 논문에서 제안한 모델은 여러 Benchmark 모델을 능가하는 결과를 보여주었다. 또한 본 논문에서는 확률적 미니배치를 통해 더 큰 데이터셋에서 학습될 수 있다는 것을 보여준다.
미래에 이 모델을 더욱 크고 Multi-modal 형태의 데이터 (Text, Image, Graph-based Information으로 구성된)에도 적용할 수 있기를 바란다. 이러한 세팅에서는 GCMC 모델은 Recurrent 또는 Convolutional Neural Network와 결합하여 사용될 수 있을 것이다.
더욱 확장하기 위해서는 효율적인 근사 방법이 필요한데, 예를 들어 Local Neighborhood를 Sub-sampling하는 방법이 그 예가 될 수 있을 것이다. 이 방법에 대해서는 Inductive Representation Learning on Large Graphs라는 논문을 참고하길 바란다. 이 논문에 대한 리뷰는 곧 블로그에 업데이트될 것이다.
마지막으로 Attention Mechanism은 이러한 종류의 모델의 성능을 더욱 향상시키는 방법이 될 수 있을 것이다.