이 글에서는 2019년 6월 Nazneen Fatema Fajani 등이 발표한 Explain Yourself! Leveraging Language Models for Commonsense Reasoning 논문을 살펴보도록 한다.

이 논문에서는 CoS-E라는 상식 설명문(Common Sense Explanations)에 관한 데이터셋을 만들어 공개했다. 여기에서 찾아볼 수 있다(논문의 링크로 들어가보면 저장 위치가 바뀌었다고 한다).

중요한 부분만 적을 예정이므로 전체가 궁금하면 원 논문을 찾아 읽어보면 된다.

Explain Yourself! Leveraging Language Models for Commonsense Reasoning

논문 링크: Explain Yourself! Leveraging Language Models for Commonsense Reasoning

Dataset: CoS-E

초록(Abstract)

딥러닝 모델들은 상식추론(Commonsense Reasoning)이 필요한 task에서는 낮은 성능을 보여, 입력에는 당장 나타나지 않는 어떤 정보에 대한 지식이나 추론이 필요하게 하였다. 우리(이 논문의 저자)는 CoS-E(Common Sense Explanations)라 부르는, 1) 일련의 자연어와 2) 강조된 구문 두 가지 형태로 구성된 새로운 데이터셋을 수집했다. CAGE(Commonsense Auto-Generated Explanation) Framework에서 학습 및 추론 단계에서 사용될 수 있는 설명문(explanations)을 자동으로 생성하도록 언어모델을 학습시켰다. CAGE는 상식질답(CommonsenseQA) task에서 10%만큼 State-of-the-art를 뛰어넘었다. 우리는 또한 out-of-domain으로의 전이학습을 포함하여 사람이 그리고 기계가 자동생성한 설명문을 전부 사용하여 DNN에서 상식추론 문제를 연구할 것이라 하였다. 실험결과는 상식추론에 관해 언어모델을 효과적으로 조정(Leverage)할 수 있음을 시사한다.

1. 서론(Introduction)

상식추론(Commonsense Reasoning)은 현대 기계학습 방법에서 도전적인 과제이다. 설명문(Explanations)은 모델이 학습하는 추론을 말로 표현하는 방법이다. 상식질답(Commonsense QA, CQA)는 상식추론 능력을 가진 자연어처리(NLP) 모델을 개발하기 위한 다지선다형 질답 데이터셋이다. 이와 관련해 많은 노력이 있었지만 뚜렷한 발전이 없었다.
이 논문의 저자들은 CQA에 더해 상식추론을 위한 사람의 설명문을 수집했고 이를 CoS-E라 하였다. CoS-E는

1. 자유형식의 일련의 자연어(보통 문장)
2. 정답을 추론하는 데 중요하다고 사람이 판단한 문장의 일부를 강조한 부분

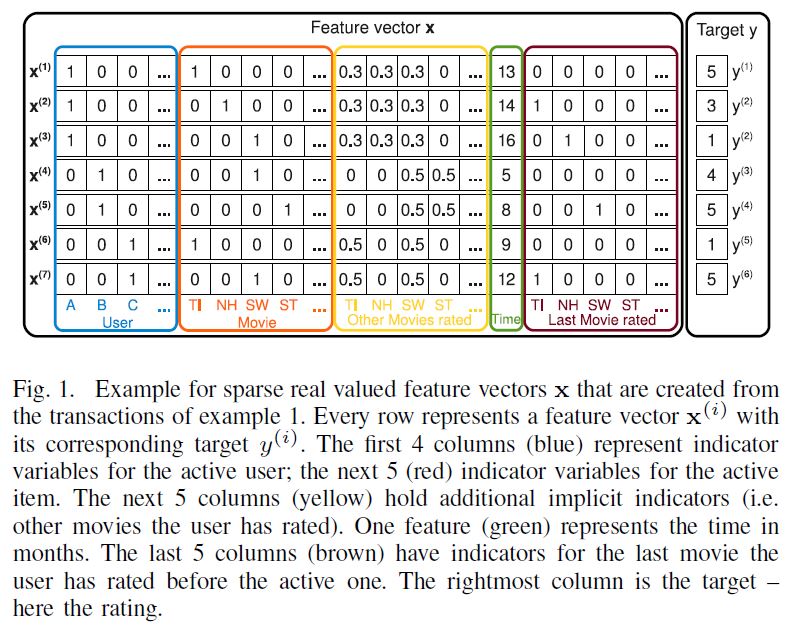
두 가지 형태로 존재한다. 아래 그림에서 Question과 Choicse(3개)는 CQA dataset의 일부이며, CoS-E는 1) CoS-E 부분의 문장과 2) Question에서 노란색으로 강조된 부분을 포함한다.

Talmor et al. (2019)에서는 Google search를 활용하여 각 질답 당 100개의 snippet으로부터 문맥정보를 추출해내는 것은 ELMo 표현에 self-attention layer를 쓴 모델이자 현재 SOTA(state-of-the-art) 모델인 BiDAF++를 사용해도 CQA에서 정답률을 향상시키지 못한다고 하였다.

이에 반해, 우리는 상식추론에 유용한 설명문(explanations)을 생성하는 사전학습된 모델을 조정하였다. CQA를 위한 설명문을 생성하는 framework로 CAGE(Commonsense Auto-Generated Explanations)를 제안한다. 우리는 상식추론 문제를 두 단계로 나누었다:

1. CQA sample과 그에 맞는 CoS-E 설명문을 언어모델에 입력으로 준다. 언어모델은 CQA 질답에 기초하여 CoS-E 설명문을 생성하도록 학습된다.
2. 언어모델은 CQA의 학습(training)과 검증(validation) 세트 안에 있는 각 sample에 대해 설명문을 생성하도록 한다. 이 CAGE 설명문은 원래의 질문, 선택지, 언어모델의 출력값에 이어붙여 두 번째 상식추론 모델의 입력으로 들어간다.

이 2단계의 CAGE framework는 기존 최고의 baseline보다 10% 초과 달성한 결과를 얻었으며 그 예측값을 정당화(justify)하는 설명문을 생성하였다. 아래 그림은 이 접근법을 개략적으로 보여준다.

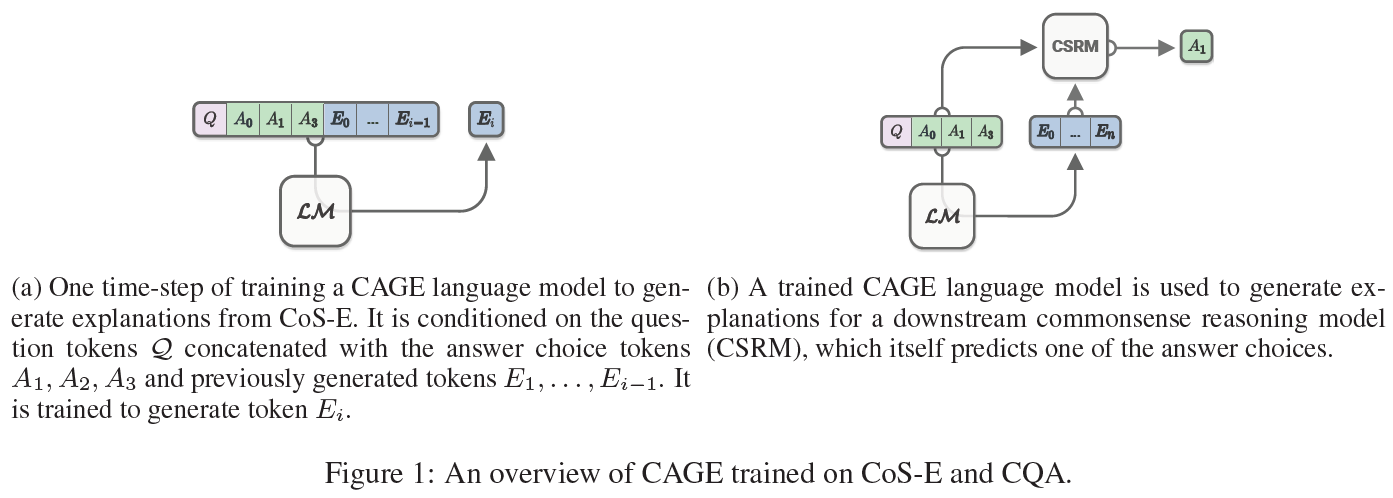
요약하면, 이 논문은 상식추론을 위한 새로운 CoS-E 데이터셋을 소개하였고, CQA v1.0에서 65%의 정답률을 보인 ‘설명문을 자동 생성하는’ CAGE framework를 제안하였다.

참고로, 이 논문이 제출되기 직전 CQA는 v1.11를 공개하였는데, 질문에 대한 선택지가 3개에서 5개로 늘어났다. 더 도전적인(challenging) 과제로 바뀌었다.

2. 배경이론과 관련 연구(Background and Related Work)

논문에 2.1. section이라 소개하진 않았지만 목차를 위해 넣었다.

2.1. Commonsense Reasoning

자연어에 포함된 상황이나 사건의 관계를 예측하도록 요구하는 데이터셋이 최근 몇 개가 소개되어 왔다.

• 여러 타당한 결말 중 가장 올바른 스토리 결말을 선택하는 Story Cloze(혹은 ROC Stories)
• 초기 상황에 기초하여 다음 장면을 예측하는 SWAG(Situations with Adversarial Generations)

이러한 데이터셋에 대해서는 GPT나 BERT이 이미 사람 수준의 성능을 내지만, 대명사가 어떻게 다른 부분과 연관이 되어 있으며 어떻게 세상의 지식과 상호작용을 하는지 등에 관해서는 별로 성공적이지 못했다.

CQA는 9500개의, 질문 + 1개의 정답 + 2개의 헷갈리는 오답으로 구성되어 있는 데이터셋으로 단지 분포상의 편향(biases)에서 정보를 얻기보다는 질문에서 추론하도록 하는 것을 요구하지만, 언어적인 면에서 좋지 않은 쪽으로 편향되어 있음이 발견되었다. 이를테면, 여자와 관련된 부분에서는 부정적인 의미의 문맥이 있다거나 하는.

SOTA 언어모델은 사람에 비해 CQA 데이터셋에서 굉장히 낮은 성능을 보인다. CQA는 모델의 상식추론 능력을 측정하는 benchmark를 제공함에도 정확히 어떤 부분이 모델이 추론을 행하는지는 여전히 불확실하다. CoS-E는 이 benchmark에 더해, 다른 한편으로 모델의 추론능력을 연구, 평가 및 분석할 수 있도록 하는 설명문을 제공한다.

2.2. Natural language explanations

Lei et al.에서는 감정분석 접근법의 타당성을 입증할 수 있는, 어떤 추론 결과를 내기 위해 필요한 구문을 입력에서 강조(선택)하는 방식을 제안했다. 분류데이터를 위한 사람이 만든 자연어 설명문은 의미분석을 학습하기 위해 사용되어왔고 분류기를 학습시키는 데 사용할 수 있는, noisy한 분류 데이터를 생성하였다. 그러나 전이성(interpretability)은 SNLI(Stanford Natural Language Inference)에서 성능저하를 보인다고 한다.
그러나, e-SNLI와는 다르게, CQA를 위한 설명문은 설명-예측 단계로 성능을 향상시킬 수 있다. 또한 VQA에도 사용 가능하며, 자동생성된 것과 사람이 만든 설명문을 함께 사용하는 것이 따로 사용하는 것보다 더 좋은 결과를 내었다.

2.3. Knowledge Transfer in NLP

자연어처리는 Word2Vec이나 GloVe와 같은 사전학습된 단어벡터를 통한 지식의 이전(transfer)에 의존한다. 맥락과 관련된(contextualized) 단어벡터의 사용은 여러 task에서 획기적인 성공을 이뤘다. 이러한 모델들은 적은 수의 parameter만 학습시킬 필요가 있고 따라서 적은 데이터만 갖고 있어도 학습이 가능하다는 장점이 있다. 잘 fine-tuned 된 언어모델은 설명문 생성과 함께 조정될 때 더 효과적이며 언어적으로 상식 정보를 얻어낸다는 점도 실험적으로 증명되었다.

3. Common Sense Explanations(CoS-E)

이 CoS-E 데이터셋은 아마존의 MTurk(Amazon Mechanical Turk)를 통해 수집되었다. CQA 데이터셋은 question token split 과 random split 두 개로 이루어져 있다. CoS-E 데이터셋과 이 논문의 모든 실험은 더 어려운 random split 을 사용하여 진행되었다. CQA v1.11에 대한 CoS-E도 만들었다.

사람들은 질문, 선택지, 정답이 주어지면 “왜 이것이 가장 적절한 답으로 예측되었는가?”라는 질문을 받는다. 그리고

• 주어진 정답이 왜 정답일지를 알려줄 수 있는 부분을 질문에서 선택하며,
• 또한 이 질문 뒤에 숨어 있을 상식적인 내용을 설명하는 자연어 문구를 작성하도록

지시받았다. (참고: 이는 CoS-E 데이터셋의 설명과 일치함.)

그래서 CQA v1.0에 대해 7610(train random split) + 950(dev random split)개의 설명문을, v1.11에 대해 9741 + 1221개의 설명문을 수집하였다. 또한 여기서부터는 질문에서 선택된 부분을 CoS-E-selected, 작성한 자연어 문구(open-ended)는 CoS-E-open-ended 라 한다.

MTurk에서는 사람들의 답변의 품질이 좋다는 것을 보장할 수 없기 때문에, 다음과 같은 처리를 거쳤다:

• 질문에서 아무 것도 선택하지 않거나
• 작성한 설명문이 4단어 이하이면 답변하지 않은 것으로 처리되며
• ‘이 정답은 답이 되는 유일한 것이다’와 같은 답변은 모두 제거하였다.

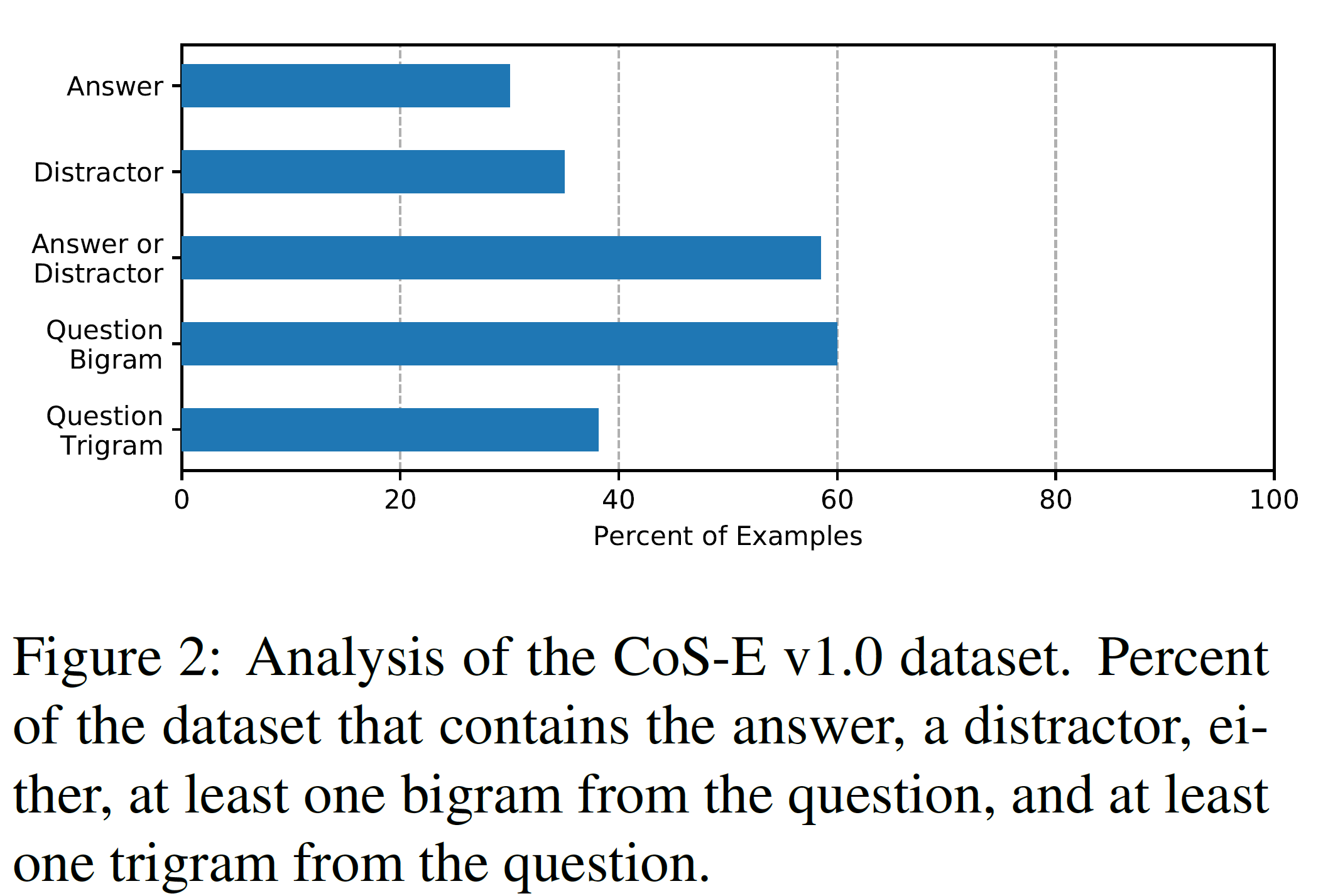
위 그림은 CoS-E v1.0 데이터셋의 분포를 보여준다.
이 논문의 실험에서는 CoS-E를 오직 학습(training) 과정에만 사용하여 SOTA 결과를 얻었으며, CoS-E 데이터셋을 사용한 경우가 그렇지 않은 경우보다 성능이 더 좋다는 것을 실험적으로 보였다.

CoS-E는 crowd-sourcing으로 얻어진 것이기 때문에 noisy할 수는 있지만 그만큼 다양성이 확보되었으며 충분한 품질을 갖고 있는 것으로 보인다고 한다.

4. 알고리즘(Algorithm)

CAGE(Commonsense Auto-Generated Explanations)를 제안하고 이를 CQA task에 적용한다. CAGE는 언어모델에 의해 생성되었으며 분류모델의 보조 입력으로 사용된다. CQA 데이터셋의 각 샘플은 질문 $q$, 선택지 $c0, c1, c2$, 정답 레이블 $a$로 구성된다. CoS-E 데이터셋은 왜 $a$가 가장 적절한지를 말해주는, 사람이 만든 설명문 $e_h$가 추가된다. CAGE의 출력은 생성한 설명문 $e$가 $e_h$에 가까워지도록 학습하는 언어모델이다.

4.1. Commonsense Auto-Generated Explanations(CAGE)

CAGE를 분류모델에 적용하기 위해, 언어모델(LM)을 CoS-E 데이터셋으로부터 설명문을 생성하도록 fine-tune했다. 이 언어모델은 여러 transformer 레이어로 이루어진, 사전학습된 OpenAI GPT이다.
여기서, 설명문 생성과 관련하여 두 가지 설정:

1. 설명 후 예측(explain-and-then-predict(reasoning))
2. 예측 후 설명(predict-and-then-explain(rationalization))

으로 진행하였다.

Reasoning

이 방법이 이 논문의 주된 접근법이다. 언어모델은 질문, 선택지, 사람의 설명문으로 fine-tuned 되었으며 실제 정답 label로는 학습되지 않았다. 그래서, 학습하는 동안 입력 문맥(context)은 다음과 같이 정의된다:

$ C_{RE} = “q, c0, c1 \ or\ c2? $ commonsense says

모델은 조건부 언어모델링 목적함수에 따라 설명문 $e$를 생성한다:

[\sum_i log P (e_i \vert e_{i-k}, …, e_{i-1}, C_{RE} ; \Theta )]

$k$는 문맥범위(context window)의 크기(이 논문에서는 항상 $ k \ge \vert e \vert $로 전체 설명문이 문맥에 포함됨)이다.
이 방식은 상식 질답 문제의 추론 단계에서 추가 문맥정보를 전달하기 위해 설명문을 자동생성하므로 reasoning 이라 부르기로 하였다.

또한 실험의 완전성을 위해, 추론과 설명의 단계를 바꿔보았는데, 그것이 다음에 설명할 rationalization이다.

Rationalization

언어모델은 post-hoc rationalization을 생성하기 위해 입력과 더불어 예측된 label을 조건으로 한다. 그래서 fine-tuning 단계에서 입력 문맥은 다음과 같다.

$ C_{RE} = “q, c0, c1 \ or\ c2?\ a$ because

목적함수는 reasoning의 것과 유사하지만 모델은 학습 중에도 입력 질문에 대한 실제 정답을 볼 수 있다. 언어모델은 예측 label에 조건을 갖기 때문에 설명문은 상식추론으로 고려될 수 없다. 대신 설명문은 모델이 더 이해 및 해석하기 쉽도록 만드는 rationalization 을 제공한다. 이 접근법은 현 최고의 모델보다 6% 더 높은 성능을 가지며 품질 좋은 설명문을 생성해 낸다.

CAGE에 대해서, 최대길이 20, batch size 36, 10 epoch 동안 학습시겨 가장 좋은 BLEU 점수와 perplexit를 갖는 모델은 선택했다. 학습률(learning rate)는 $1e^{-6}$, 초반 0.002까지 선형적으로 증가하다가(warm-up lr) 0.01만큼 decay되는 방식을 채택했다.

4.2. Commonsense Predictions with Explanations

CoS-E의 사람의 설명문이나 언어모델의 추론 중 하나를 갖고 있을 때 CQA task에 대한 예측모델을 학습시킬 수 있다. 모든 BERT 모델의 입력 샘플의 시작 부분에 들어가는 [CLS] token에 해당하는 최종 상태(final state)를 입력으로 받는 이진 분류기를 추가함으로써 다지선다형 질문 task에 fine-tuning 될 수 있는 BERT를 분류기로 사용하였다. 이를 CQA task에도 적용했는데,

• 데이터셋의 각 샘플에 대해
  • BERT를 fine-tuning하기 위한 일련의 세 입력을 구성하고
  • 각 입력은 (질문, 구분자 [SEP], 선택지 중 하나)로 구성된다.
• 만약 CoS-E나 CAGE의 설명문을 추가한다면
  • 각 입력은 (질문, 구분자 [SEP], 설명문, 구분자 [SEP], 선택지 중 하나)로 이루어진다.

BERT를 위해 설명문은 한 질문에 대해 같은 입력표현을 공유한다. 선택지에 대해서도 공유하는 것은 약간의 성능저하를 보였다.

4.3. Transfer to out-of-domain datasets

Out-of-domain NLP 데이터셋에 fine-tuning 없이 전이학습을 시키는 것은 낮은 성능을 기록한다고 알려져 있다.
이 논문에서는 CQA에서 SWAG와 Story Cloze Test(둘 모두 CQA같은 다지선다형이다)에 대해서 전이학습을 연구했다. CQA에 fine-tuned된 GPT 언어모델을 SWAG에 대한 설명문을 생성하기 위해 사용하였다. 그리고 이를 통해 BERT 분류기를 학습시켜 두 데이터셋에 평가를 진행했다.

5. 실험 결과(Experimental Results)

모든 모델은 BERT에 기초하며, CoS-E나 CAGE를 쓰지 않을 것이 baseline이 되며, 모든 실험은 CQA dev-random-split에서 수행되었다. 또한 final test split에서도 핵심 모델을 평가하였다.

CoS-E 설명을 사용할수록 성능이 높아짐을 확인할 수 있다.

아직 사람에 비해서는 모든 모델이 한참 못 미치지만, CoS-E와 CAGE를 사용함으로써 성능이 좋아졌다.

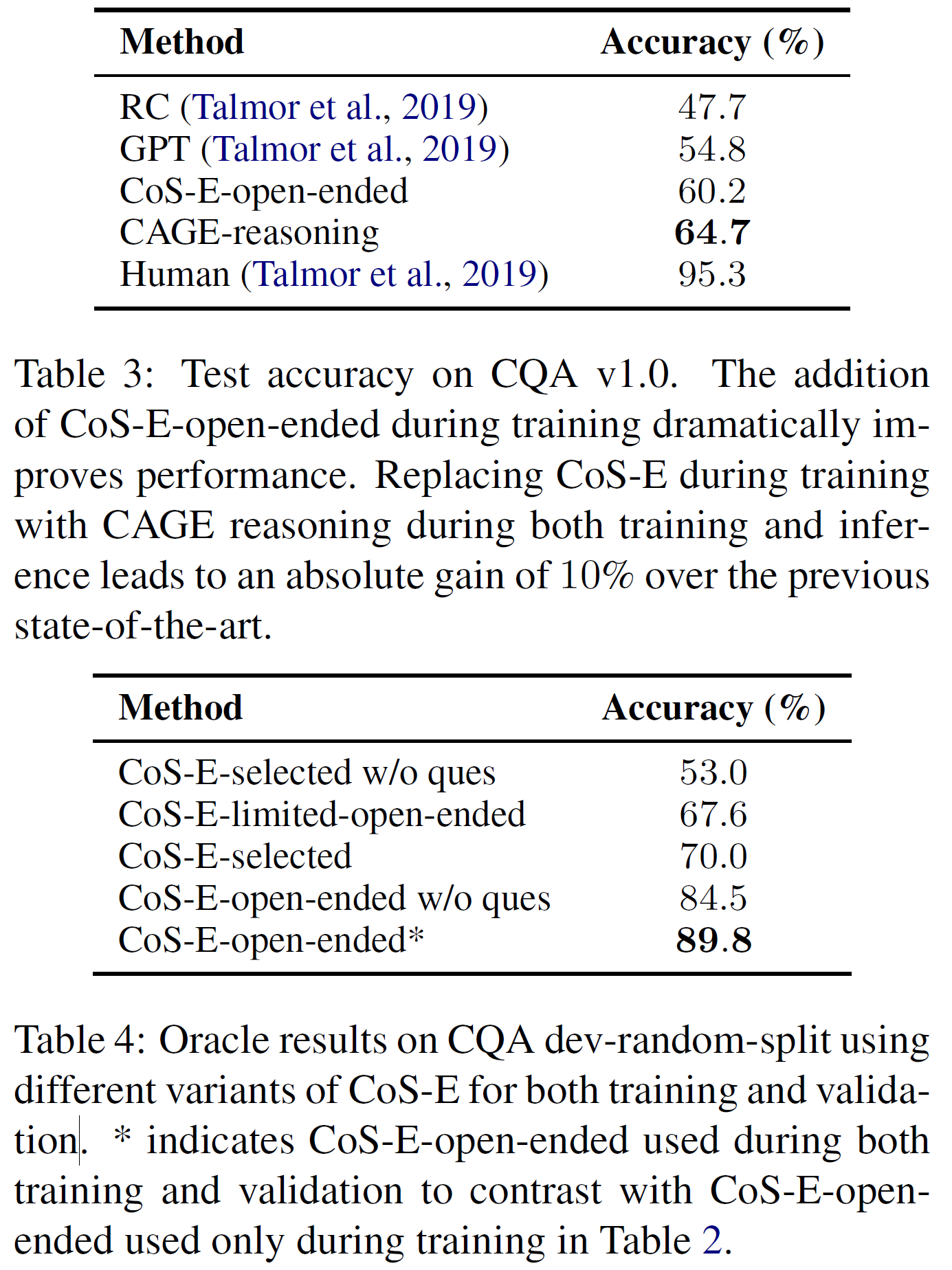
위의 표의 마지막에 있는 89.8%이라는 수치는 설명문을 제공받은 사람은 실제 정답을 갖고 있었기 때문에 공정한 수치는 아니라고 하지만, CoS-E-open-ended를 사용했을 때 얼마만큼 성능을 향상시킬 수 있을지에 대한 상한선을 보여준 것이라 한다. 또한 질문이 없는 상태에서 진행한 실험도 있는데, 질문 없이 어떤 정답이 가장 정답일 것 같은지를 설명문을 보고 판단하는 실험이다.
그리고 open-ended CoS-E의 경우 질문에 이미 있는 쓸모 있는 정보를 알려주는 것을 넘어 중요한 정보를 제공한다는 것을 보여준다.

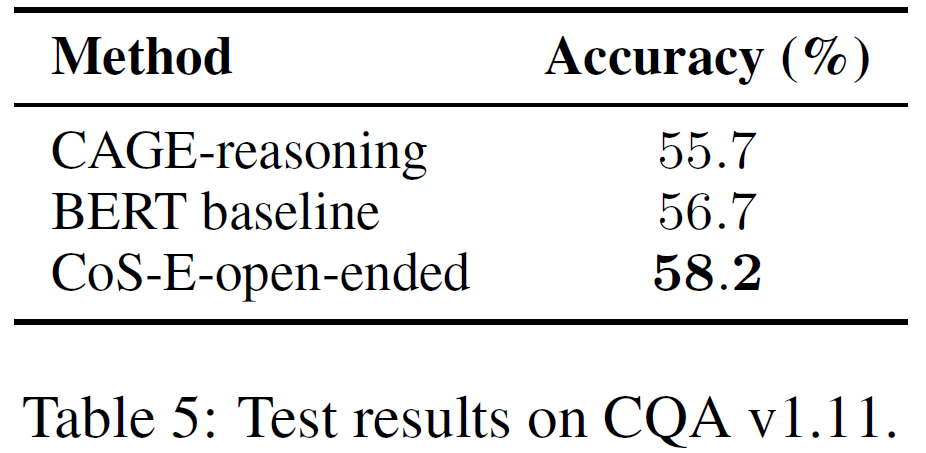
CQA v1.11에 대한 실험도 진행하였고 그 결과는 위 그림에서 볼 수 있다.

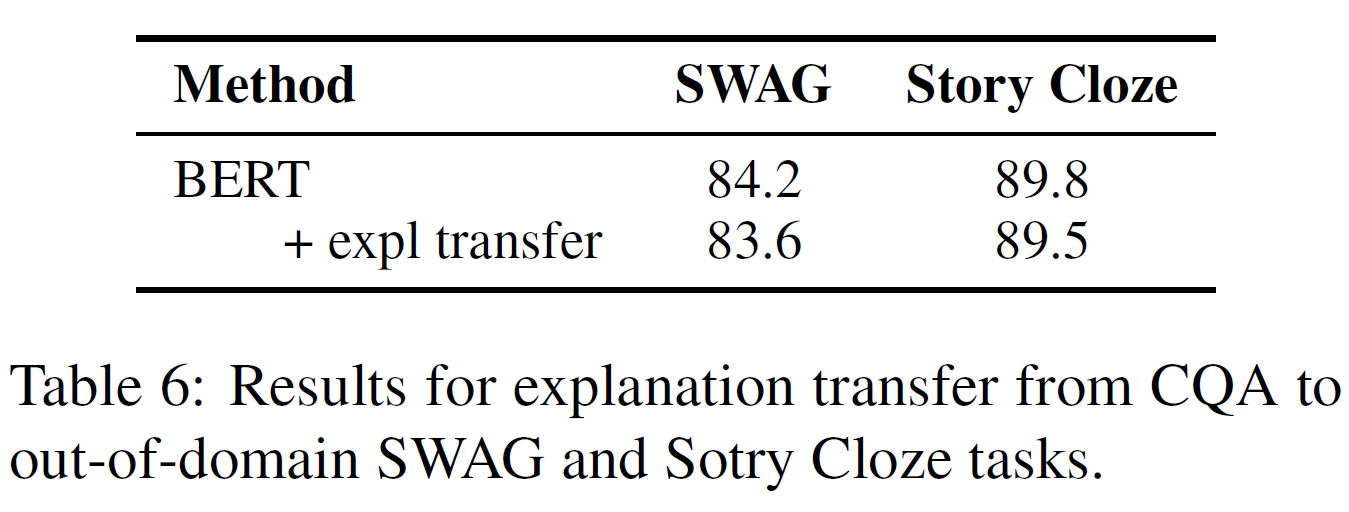
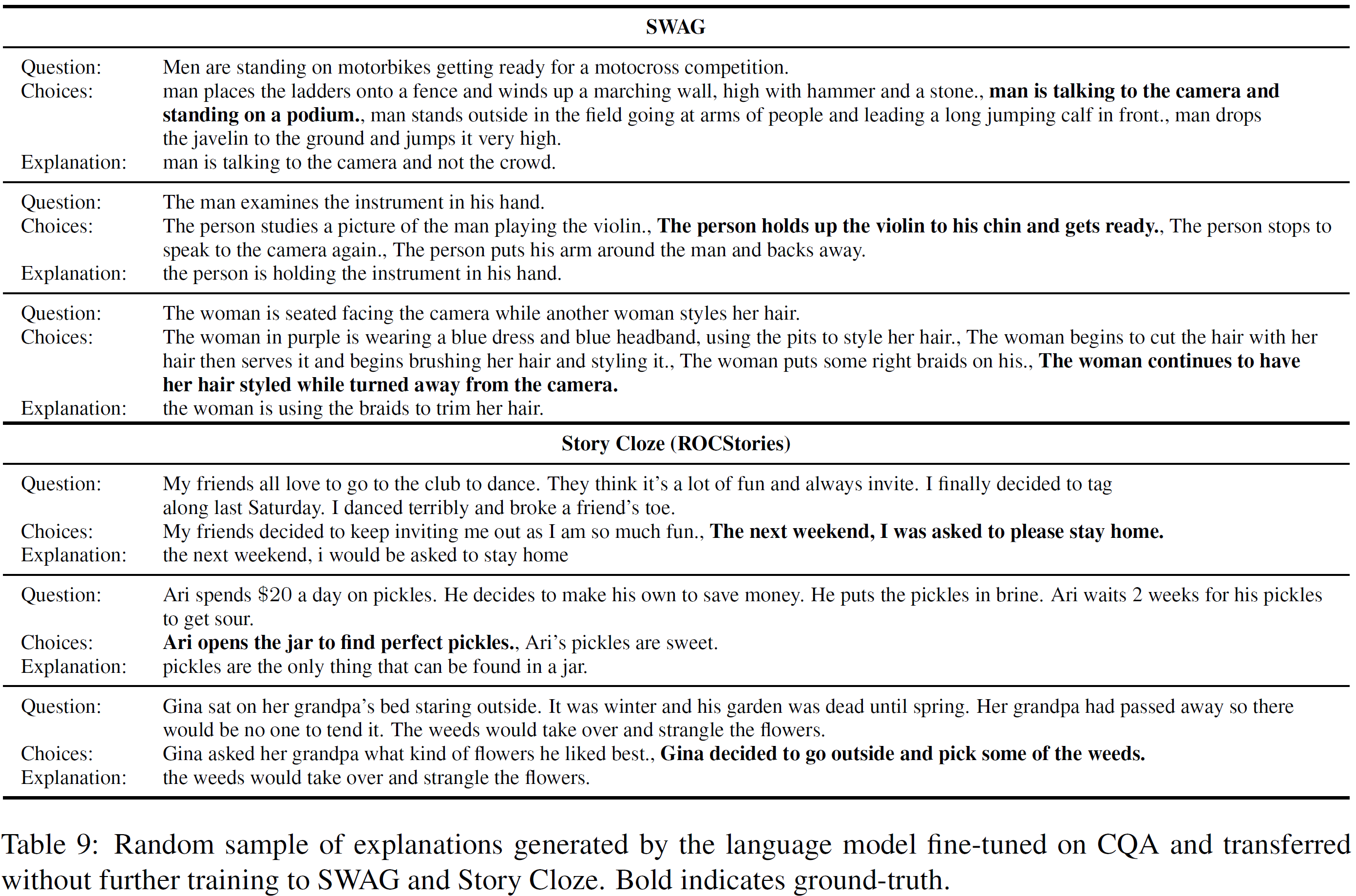
전이학습에 대한 결과는 아래 그림에서 볼 수 있는데, CQA에서 SWAG와 Story Cloze로 전이된 설명문을 추가한 경우 약간의 성능저하가 있음을 보였다.

6. 분석 및 토의(Analysis and Discussion)

CAGE-reasoning은 72%의 성능을 보였는데, CoS-E-open-ended의 모든 정보를 활용한다면 최대 90% 정도까지 성능이 올라갈 수 있음을 보였기 때문에, 추가적인 분석이 더 필요하다.
CAGE-reasoning과 CoS-E-open-ended 간 BLEU 점수는 4.1이며 perplexity는 32를 보였다.

아래 그림은 CQA, CoS-E, CAGE 샘플을 가져온 것인데, CAGE-reason이 일반적으로 CoS-E보다 조금 더 간단한 구성을 보이는데, 이 조금 더 선언적인 부분이 CoS-E-open-ended보다 더 유익한 경우가 있다(실제 단어 차이는 거의 없다). CAGE-reasoning은 43%의 경우에서 선택지 중 적어도 하나를 포함하는데, 모델의 실제 예측 선택지는 21%만이 그러하였다. 이는 답을 직접적으로 가리키는 것보다 더 효과적인 부분이 CAGE-reasoning에 있음을 보여준다.

CAGE-rationalization이 CAGE-reasoning보다 조금 더 나은 것 같기도 하지만, 실제 질문 없이 정답을 추측하는 부분에서는 별 향상이 없다.

CoS-E나 CAGE가 noisy하다고 해도, 모델의 성능이 낮은 것이 이것 때문이라 볼 수는 없다. 만약 CQA의 세 선택지 중 하나를 호도하는 선택지로 일부러 바꾼 경우 모델의 성능은 60%에서 30%로 떨어졌다. 에러의 70%는 호도하는 설명문에 의해 만들어졌고, 그 중 57%는 대신 CoS-E 설명문으로 학습된 모델에 의해 올바르게 정답을 맞췄다. 이는 유익한 설명문의 효과를 보여준다.

CQA v1.11에서는 BERT를 1.5% 차이로 앞섰는데, CQA v1.11에서 잘못 예측한 예시는 아래에서 볼 수 있다. 잘못 예측한 것 중 많은 부분은 생성된 설명문에 맞는 정답을 포함하는 경우가 있었다(dresser drawer과 cleanness 등). 이러한 경우는 관련 있는 정보에 더 집중하도록 하는 명시적인 방법이 필요로 함을 보여준다. 그리고 “forest”와 “compost pile” 같은 의미적으로 비슷한 다른 선택지를 고르는 경우도 빈번했는데, 이는 새로운 CQA 데이터셋에서 설명문을 단지 덧붙이는 것만으로는 충분하지 않음을 보여준다.

SWAG와 Story Cloze에 맞춰 생성한 설명문은 유익한 정보를 담고 있는 것을 발견했지만, 전이학습에 대한 실험에서 분류기가 이를 제대로 활용하지는 못했다.

7. 결론 및 향후 연구(Conclusion and Future Work)

CoS-E라는 새로운 데이터셋을 제시하였고, CAGE framework를 제안하였으며, 여기서 생성된 설명문(explanations)은 예측을 위해 분류기에서 효율적으로 사용될 수 있었다. 이로써 단지 SOTA를 달성한 것 뿐만 아니라, 이해할 수 있는(interpretable) 상식추론과 관련해 설명문을 연구하는 새로운 길을 열었다.

CAGE는 답을 예측하기 위한 사전 작업으로 설명문을 생성하는 데 집중했는데, 설명문을 통한 언어모델은 정답 예측에 있어 함께 학습될 수도 있다. 이는 더 많은 task에 적용될 수 있을 것이다. 많은 task에 대해 충분한 설명문 데이터셋(CoS-E)가 있으면 다른 task에 대해서도 유용한 설명문을 생성하는 언어모델을 만들 수도 있다.

그리고, 설명문은 편향이 없어야 할 것이다. 예를 들어 CQA에서는 ‘여성’과 ‘부정적인 문맥’의 연관도가 다른 쪽에 비해 더 높았는데, 이러한 편향이 있음은 모델 학습에 있어 분명 고려되어야 한다.

Acknowledgements

언제나 있는 감사의 인사. 그림과 reviewer 등등

Refenrences

논문 참조. 많은 레퍼런스가 있다.

1. Introduction

파이썬에서 에러를 처리하고 관리하는 데에는 다양한 이유가 있다. 실제 Applicaion 상에서 에러가 발생하지 않도록 개발과 테스트 단계에서 미리 에러를 식별하고 수정하는 것은, 어떤 프로그램을 만들 때 굉장히 중요한 과정이라고 할 수 있다.

기본적으로 파이썬에서는 BaseException이라는 class를 통해 에러를 관리하도록 도와준다. 이 class는 모든 내장 exception들의 base class이다. 만약 사용자가 직접 에러 class를 만들고 싶을 때는 이 에러를 사용하는 것이 아니라 Exception class를 사용해야 한다.

코딩을 하다보면 여러 종류의 에러를 보았을 것이다. 예를 들어 아래와 같은 에러가 대표적일 것이다.

ValueError
AssertionError
FileNotFoundError
SyntaxError

대체 이 에러들은 다 어떻게 만들어지고, 어떻게 구성되는 것일까? 사실 이 에러들은 앞서 설명한 BaseException class의 하위 class로 이루어진다. 그 전체 구조는 아래와 같다.

BaseException
 +-- SystemExit
 +-- KeyboardInterrupt
 +-- GeneratorExit
 +-- Exception
      +-- StopIteration
      +-- StopAsyncIteration
      +-- ArithmeticError
      |    +-- FloatingPointError
      |    +-- OverflowError
      |    +-- ZeroDivisionError
      +-- AssertionError
      +-- AttributeError
      +-- BufferError
      +-- EOFError
      +-- ImportError
      |    +-- ModuleNotFoundError
      +-- LookupError
      |    +-- IndexError
      |    +-- KeyError
      +-- MemoryError
      +-- NameError
      |    +-- UnboundLocalError
      +-- OSError
      |    +-- BlockingIOError
      |    +-- ChildProcessError
      |    +-- ConnectionError
      |    |    +-- BrokenPipeError
      |    |    +-- ConnectionAbortedError
      |    |    +-- ConnectionRefusedError
      |    |    +-- ConnectionResetError
      |    +-- FileExistsError
      |    +-- FileNotFoundError
      |    +-- InterruptedError
      |    +-- IsADirectoryError
      |    +-- NotADirectoryError
      |    +-- PermissionError
      |    +-- ProcessLookupError
      |    +-- TimeoutError
      +-- ReferenceError
      +-- RuntimeError
      |    +-- NotImplementedError
      |    +-- RecursionError
      +-- SyntaxError
      |    +-- IndentationError
      |         +-- TabError
      +-- SystemError
      +-- TypeError
      +-- ValueError
      |    +-- UnicodeError
      |         +-- UnicodeDecodeError
      |         +-- UnicodeEncodeError
      |         +-- UnicodeTranslateError
      +-- Warning
           +-- DeprecationWarning
           +-- PendingDeprecationWarning
           +-- RuntimeWarning
           +-- SyntaxWarning
           +-- UserWarning
           +-- FutureWarning
           +-- ImportWarning
           +-- UnicodeWarning
           +-- BytesWarning
           +-- ResourceWarning

굉장히 많다. 이 에러와 경고(Warning)들을 다 외우고 있을 필요는 없을 것이다. 하지만 인지는 하고 있는 편이 좋다.

2. Exception 처리: try, except, finally

2.1. 일반적인 처리

try 블록을 수행하는 과정에서 에러가 발생하면 except 블록이 수행된다. 만약 에러가 발생하지 않았다면, except 블록은 수행되지 않는다. 만약 에러의 발생 유무와 상관없이 꼭 어떤 과정을 수행하고 싶다면 finally 블록에 이를 담으면 된다.

# 예시 1
try:
    import nothing
except ImportError as error:
    print(error)
finally:
    import numpy as np
    print(np.array([1, 2]))


No module named 'nothing'
[1 2]

# 예시 2
try:
    print(3/0)
except ZeroDivisionError:
    print("Error: You cannot divide integer by zero")

Error: You cannot divide integer by zero

참고로 assert 조건, "에러 메시지" 인 assert 구문을 통해 에러를 관리할 수도 있다.

2.2. 특별한 요청

아래에는 위와는 다르게 조금은 특별한(?) 요청을 하고 싶을 때 사용할 수 있는 기능들이다.

• 만약 에러를 그냥 회피하고 싶다면 except 블록에 pass를 입력하면 된다.
• Exception이 발생하였을 때 프로그램을 중단하고 싶으면 raise SystemExit을 except 블록에 입력하면 된다.
• Exception을 일부러 발생하고 싶을 때에도 raise 구문을 사용하면 된다.

3번 째 경우에 대한 예시를 첨부하겠다. BaseBandit이라는 부모 class가 있고, 사용자는 이 부모 class를 상속받아 TalkativeBandit이라는 자식 class를 만들고 싶다고 하자.

그런데 이 때, 자식 class에 반드시 operate이란 메서드를 구현하도록 미리 설정을 해두고 싶다. 모니터 구석에 메모를 해두는 것 외에 방법이 없을까? 이 때 부모 class인 BaseBandit에 미리 아래와 같은 코드를 구현해 놓으면 원하는 바를 쟁취할 수 있을 것이다.

# 부모 class 구현
class BaseBandit:
    def operate(self):
        raise NotImplementedError

# 자식 class 구현
class TalkativeBandit(BaseBandit):
    def stay(self):
        print("Don't talk")

tb = TalkativeBandit()

# 자식 class에서는 operate 메서드를 구현하지 않았으므로
# 부모 class의 operate 메서드가 호출된다.
tb.operate()

# 에러가 발생한다.
Traceback (most recent call last):
  File "C:\Users\...\interactiveshell.py", line 2961, in run_code
    exec(code_obj, self.user_global_ns, self.user_ns)
  File "<ipython-input-17-fdf0f46c74b7>", line 1, in <module>
    tb.operate()
  File "<ipython-input-12-af85936c9668>", line 3, in operate
    raise NotImplementedError
NotImplementedError

operate 메서드를 제대로 구현한다면, 별 문제 없이 코드를 진행할 수 있을 것이다.

3. Exception 추적

바로 위의 예시를 보자. Traceback (most recent call last)란 문구를 볼 수 있을 것이다. 이는 Exception을 역으로 추적한다는 뜻이다.

사용자가 직접 추적 과정을 만들고 싶을 때 stack trace를 표시하고 출력하는 traceback 모듈과 로그 기록을 관리하는 logging 모듈을 사용하면 편리하다.

가장 기초적인 추적 방법은 아래와 같다.

import traceback

try:
    tuple()[0]
except IndexError:
    print("--- Exception Occured ---")
    traceback.print_exc(limit=1)

# 출력 결과
--- Exception Occured ---
Traceback (most recent call last):
  File "<ipython-input-19-0acccd16d042>", line 2, in <module>
    tuple()[0]
IndexError: tuple index out of range    

빈 튜플에 indexing을 시도했으므로 에러가 발생하는 것은 당연하다.
그 에러는 IndexError 인데, 우리는 traceback.print_exc 메서드를 통해 stack trace 정보를 출력할 수 있다.

limit=None이 기본이며 이 때는 제한 없이 stack trace를 출력한다. 위 예시와 같이 1을 입력하면 단 한 개의 stack trace 정보를 출력한다는 뜻이다. file, chain argument 설정을 통해 파일 출력 위치를 설정하거나 연쇄적인 Exception 출력 설정을 관리할 수 있다.

왜 이런 과정을 거쳐야 할까? 만약 이와 같이 try-except를 통해 Exception을 관리해주지 않는다면, 우리는 모든 에러를 잡기 전까지 프로그램 전체를 돌릴 수 없을 것이다.

이번에는 logging 모듈과 합작하여 Exception을 추적해보자.

import traceback
import logging

logging.basicConfig(filename="example.log", format="%(asctime)s %(levelname)s %(message)s")

try:
    tuple()[0]
except IndexError:
    logging.error(traceback.format_exc())
    raise

# 출력 결과
Traceback (most recent call last):
  File "C:\Users\...\interactiveshell.py", line 2961, in run_code
    exec(code_obj, self.user_global_ns, self.user_ns)
  File "<ipython-input-18-16da8da0daa5>", line 6, in <module>
    tuple()[0]
IndexError: tuple index out of range

logging 모듈을 통해 우리는 example.log라는 파일에 에러에 관한 기록을 해둘 수 있었다.
이 파일에는 다음과 같은 로그 기록이 남아있다.

2020-01-12 18:38:50,633 ERROR Traceback (most recent call last):
  File "<ipython-input-18-16da8da0daa5>", line 6, in <module>
    tuple()[0]
IndexError: tuple index out of range

4. Exception 만들기

Exception class 상속을 통해 Exception을 직접 만들 수 있다.

import numpy as np

class SizeError(Exception):
    # 에러 메시지를 출력하고 싶으면 아래와 같은 특별 메서드를 구현해야 한다.
    def __str__(self):
        return "Size does not fit"
    
# 기준이 되는 base
base = np.eye(3)

# 비교대상인 data
data1 = np.array([[1,2], [3,4]])
data2 = np.ones((3, 3))

# np.array의 shape을 비교하는 함수이다.
def compare(base ,data):
    if base.shape != data.shape:
        raise SizeError()
    else:
        print("All Clear")

# 첫 번째 테스트
compare(base=base, data=data1)

# 첫 번째 결과
Traceback (most recent call last):
  File "C:\Users\...\interactiveshell.py", line 2961, in run_code
    exec(code_obj, self.user_global_ns, self.user_ns)
  File "<ipython-input-36-c1718418c4b8>", line 1, in <module>
    compare(base=base, data=data1)
  File "<ipython-input-35-8ec7197ddfb7>", line 3, in compare
    raise SizeError()
SizeError: Size does not fit

# 두 번째 테스트
compare(base=base, data=data2)

# 두 번째 결과
All Clear

Reference

파이썬 공식문서
참고 블로그1 참고 블로그2

1. zlib 모듈

import zlib

long_text = b"who are you" * 1000
# 압축하기
compressed = zlib.compress(long_text)

# 압축 풀기
decompressed = zlib.decompress(compressed)

# 동일한지 확인
print(long_text == decompressed)

True

2. gzip 모듈

위에서 사용한 zlib 모듈과 동일하게 compress, decompress 메서드를 사용한다. 파일을 열 때는 open 메서드를 이용하면 된다. 여는 작업에 대한 코드만 첨부한다. bzip2(bz2), lzma(xz) 형식 파일에 대해서도 유사한 메서드를 이용한다.

import gzip

with gzip.open("data.gz", "rt") as file:
    content = file.read()

3. zipfile 모듈

import zipfile

# zip 파일이 맞는지 확인
zipfile.is_zipfile("trasnactions.zip")

# zip 파일 열기
zip = zipfile.ZipFile("trasnactions.zip")

# zip 파일 내 이름 확인 및 추후 사용을 위해 저장
names = []
for name in zip.namelist():
    names.append(name)

print(names)

['transaction1.txt', 'transaction2.txt']

# 첫 번째 파일 압축 해제 과정
# 하나만 압축 해제할 때
# ZipInfo 얻기
zipinfo = zip.getinfo(names[0])
print("Filename: ", zipinfo.filename, "date_time: ", zipinfo.date_time)

Filename:  transaction1.txt date_time:  (2020, 1, 11, 19, 44, 28)

zip.extract(zipinfo)

# 전부 압축 해제할 때
zip.extractall()

# 끝나고 닫아주기
zip.close()

4. tarfile 모듈

위와 유사하다.

import tarfile

# tarfile이 맞는지 확인
tarfile.is_tarfile("transactions.tar")

tar = tarfile.open("transactions.tar")
tar.getnames()

['transaction1.txt', 'transaction2.txt']

# 하나만 압축 해제
tarinfo = tar.getmember(tar.getnames()[0])
print(tarinfo.name, tarinfo.size, tarinfo.mtime, tarinfo.mode)

transaction1.txt 74 1578739467 493

tar.extract(tarinfo)

# 전체 압축 해제
tar.extractall()
tar.close()

Reference

파이썬 라이브러리 레시피, 프리렉 https://docs.python.org/3/library/zipfile.html https://docs.python.org/3/library/tarfile.html

1. collections 모듈

1.1. collections.Counter 객체

collections 모듈에서 가장 기본을 이루는 class는 collections.Counter이다. 이 class에 argument로 반복 가능한 (iterable) 객체를 지정하거나 dictionary와 같은 mapping 객체를 지정하면 Counter 객체를 생성할 수 있다. 예를 들어보면,

import collections

counter = collections.Counter([1, 2, 3, 2])
# counter = collections.Counter({1: 1, 2: 2, 3: 1})
print(counter)

Counter({1: 1, 2: 2, 3: 1})

주석 처리된 line이 바로 후자의 방법에 해당한다. 이렇게 생성된 객체는 수정될 수 있다.

counter[1] += 1
print(counter)

Counter({1: 2, 2: 2, 3: 1})

이 외에도 여러 계산이 가능한데, 아래를 참고하길 바란다.

위 누계 연산자에서 =를 빼고 +, -, &, | 만 사용할 경우 이항 연산자로 작용한다.

또한, 이 객체에서 미등록 key를 참조한다 하더라도 KeyError는 발생하지 않는다.

print(counter[4])

0

1.2. collections.ChainMap: 사전 통합

dict1 = {'banana': 1}
dict2 = {'apple': 2}

counter = collections.ChainMap(dict1, dict2)
print(counter['apple'])

2

위와 같이 ChainMap 메서드는 여러 사전 객체를 모아 하나로 통합하는 기능을 갖고 있다. 만약 통합한 객체에 변화를 줄 경우, 원래의 사전들에도 그 변경 사항이 반영된다. clear 메서드를 사용하면 사전을 삭제할 수 있다.

1.3. collections.defaultdict: 기본 값이 있는 사전

일반적으로 사전 객체에 미등록된 key를 참조하면 KeyError가 발생한다. collections.defaultdict는 이러한 문제를 해결하기에 적합한 객체이다.

d = {'orange': 10}

def get_default_value():
    return 'default-value'

# 여기서 get_default_value와 같은 callable 객체나 None을 입력할 수 있다.
# None을 입력할 경우 일반 사전과 마찬가지로 KeyError가 발생한다.
e = collections.defaultdict(get_default_value, orange=10)
print(e['ham'])

'default-value'

만약 기본 값으로 수치 0이나 빈 사전, 리스트를 반환하고 싶다면 int, dict, list형 객체를 지정하면 된다.

e = collections.defaultdict(int)
e = collections.defaultdict(dict)
e = collections.defaultdict(list)

1.4. collections.OrderedDict: 순서가 있는 사전

for loop와 같은 과정 속에서 등록한 순서대로 요소를 추출하고 싶으면 이 class를 이용하면 좋다. 시퀀스를 이용하여 객체를 생성하면 순서대로 등록된 것을 확인할 수 있다.

mydict = collections.OrderedDict([("orange", 10), ("banana", 20)])
print(mydict)

OrderedDict([('orange', 10), ('banana', 20)])

그러나 키워드 인수나 일반 사전으로 초깃값을 등록하면 순서가 무시된다. OrderedDict 객체에는 유용한 기능들이 있는데, 아래를 참조하면 좋을 것이다.

mydict = collections.OrderedDict([("orange", 10), ("banana", 20), ("blueberry", 30), ("mango", 40)])

# popitem 에서 last=True로 하면 마지막 요소를 사전에서 삭제하고 반환하고,
# False로 하면 첫 요소에 효과를 적용한다.
mydict.popitem(last=True)

# move_to_end에서 last=True로 하면 지정한 키를 맨 끝으로 이동시키고, False이면 맨 처음으로 이동시킨다.
mydict.move_to_end(key="banana", last=True)

print(mydict)

OrderedDict([('orange', 10), ('blueberry', 30), ('banana', 20)])

1.5. collections.namedtuple

데이터를 효율적으로 관리하기에 적합한 class가 바로 namedtuple이다. 속성 이름을 지정하여 가독성을 높이고 튜플을 활용하여 원하는 요소를 쉽게 추출하도록 하게 해준다.

point = collections.namedtuple("point", "X, Y, Z")
data = point(-2, 6, 3)
print(data.Y)

6

2. heapq 모듈

데이터를 정렬된 상태로 저장하고, 이를 바탕으로 효율적으로 최솟값을 반환하기 위해서는 이 heapq 모듈을 사용하면 매우 편리하다. 사용하기 위해서는 최소 heap을 먼저 생성해야 한다. 빈 리스트를 생성해서 heapq 모듈의 메서드를 호출할 때마다 이를 heap argument의 인자로 투입해야 한다.

import heapq

heap = []

# heappush(heap, item): heap에 item을 추가함
# 주의점: keyword 인자를 입력하면 Error가 발생함
heaqp.heappush(heap, 2)
heaqp.heappush(heap, 1)

# heappop(heap): heap에서 최솟값을 삭제하고 그 값을 반환함
# 최솟값을 삭제하지 않고 참조하고 싶다면 heap[0]을 쓰자
heapq.heappop(heap)

1

이 외에도 여러 메서드를 사용할 수 있다. 만약 어떤 변화하는 시퀀스에서 최솟값을 얻고 싶다고 하자. 아래와 같은 코딩이 가능하다.

heap = [79, 24, 50, 62]

# heapify(heap): heap의 요소를 정렬함
heapq.heapify(heap)

# heappush(heap, item): heap에 item을 추가한 뒤, 최솟값을 삭제하고 그 값을 반환함
heapq.heappushpop(heap, 10)

10

# heapreplace(heap, item): 최솟값을 삭제한 뒤, heap에 item을 추가하고 삭제한 값을 반환함
# 주의점: 추가한 값 아님
heapq.heapreplace(heap, 10)

24

Reference

파이썬 라이브러리 레시피, 프리렉

본 글의 전반부에서는 먼저 Factorization Machines 논문을 리뷰하면서 본 모델에 대해 설명할 것이다. 후반부에서는 텐서플로를 활용하여 FM 모델을 구현해 볼 것이다. 논문의 전문은 이곳에서 확인할 수 있다.

1. Factorization Machines 논문 리뷰

1.0. Abstract

본 논문에서는 SVM과 Factorization model들의 장점을 결합한 FM이라는 새로운 모델을 소개한다. SVM과 마찬가지로 FM은 그 어떤 실수 값의 피쳐 벡터를 Input으로 받아도 잘 작동하는 일반적인 예측기이다. 그러나 SVM과 다르게 이 모델은 Factorized Parameter를 이용하여 모든 Interaction을 모델화하여 아주 희소한 상황에서도 Interaction들을 예측할 수 있다는 장점을 갖고 있다.

본 논문에서는 FM의 모델 방정식이 선형시간 내에서 계산되어 바로 최적화될 수 있음을 증명한다. 따라서 SVM과 달리 dual form에서의 변환(transformation)은 필요하지 않아 본 모델의 파라미터들은 해를 구할 때 Support 벡터의 도움 없이 바로 예측될 수 있다.

Matrix Factorization, SVD++, PITF, FPMC 등 다양한 모델들이 존재하는데, 이들은 오직 특정한 Input 데이터에서만 잘 작동한다는 한계를 지닌다. 반면 FM은 Input 데이터를 지정하여 이러한 모델을 따라할 수 있다. 따라서 Factorization 모델에 대한 전문적인 지식이 없더라도 FM은 사용하기에 있어 굉장히 쉽다.

1.1. Introduction

SVM은 유명한 예측 알고리즘이지만 협업 필터링과 같은 환경에서 SVM은 그리 중요한 역할을 하지 못한다. 본 논문에서는 SVM이 굉장히 희소한 데이터의 비선형적(complex) 커널 공간에서 reliable parameter(hyperplane: 초평면)를 학습할 수 없기 때문에 이러한 task에서 효과적이지 못함을 보여줄 것이다. 반면에 Tensor Factorization Model은 일반적인 예측 데이터에 대해서 그리 유용하지 않다는 단점을 가진다.

본 논문에서는 새로운 예측기인 FM을 소개할 것인데, 본 모델은 범용적인 예측 모델이지만 또한 매우 희소한 데이터 환경 속에서도 reliable parameter를 추정할 수 있다. FM은 모든 nested된 변수 간 상호작용을 모델화하지만 SVM이 Dense Parametrization을 사용하는 것과 달리 factorized parametrization을 사용한다.

FM의 모형식은 선형 시간으로 학습될 수 있으므로 파라미터들의 숫자에 따라 학습시간이 결정된다. 이는 SVM처럼 학습 데이터를 저장할 필요 없이 직접적인 최적화화 모델 파라미터의 저장을 가능하게 한다.

요약하자면 FM의 장점은 아래와 같다. 1) 굉장히 희소한 데이터에서도 파라미터 추정을 가능하게 한다. 2) 선형 complexity를 갖고 있기 때문에 primal하게 최적화될 수 있다. 3) 어떤 실수 피쳐 벡터를 Input으로 받아도 잘 작동한다.

1.2. Prediction under Sparsity

가장 일반적인 예측 문제는 실수 피쳐 벡터 x에서 Target domain T (1 또는 0)로 매핑하는 함수를 추정하는 것이다. 지도학습에서는 (x, y) 튜플이 stacked된 D라는 학습데이터셋이 존재한다고 가정된다. 우리는 또한 랭킹 문제에 대해 논의해볼 수 있는데, 이 때 함수 y는 피쳐 벡터 x에 점수를 매기고 이를 정렬하는데 사용된다. Scoring 함수는 pairwise한 학습 데이터로부터 학습될 수 있는데, 이 때 피쳐 튜플인 $ (x^(A), x^(B)) $는 $ x^(A) $가 $ x^(B) $보다 높은 순위를 지닌다는 것을 의미한다. pairwise 랭킹 관계가 비대칭적이기 때문에, 오직 positive 학습 instance만을 사용해도 충분하다.

본 논문에서 우리는 x가 매우 희소한 상황을 다룬다. 범주형 변수가 많을수록 더욱 데이터는 희소해지기 마련이다.

$m(x)$: 피쳐 벡터 x에서 0이 아닌 원소의 개수
$\overline{m}_D$: 학습 데이터셋 D에 속하는 모든 x에 대해 $m(x)$의 평균

Example 1
영화 평점 데이터를 갖고 있다고 하자. User $u \in U$가 영화(Item) $i \in I$를 특정 시점 $t \in \R$에 $r \in {1, 2, 3, 4, 5}$의 점수로 평점을 주었을 때 데이터는 아래와 같은 형상을 취할 것이다.

data S = {(Alice, Titanic, 2010-1, 5), (Bob, Star Wars, 2010-2, 3) … }

아래 그림은 이 문제 상황에서 S라는 데이터셋에서 어떻게 피쳐 벡터가 생성되는지를 보여준다.

한 행에는 하나의 User, 하나의 Item이 들어가는 것을 확인할 수 있다. 모든 영화에 대한 평점 Matrix는 행의 합이 1이 되도록 Normalized되었다. 마지막 갈색 행렬은 주황색 행렬에서 확인한 active(가장 최근에 평점을 매긴)item 바로 이전에 평점을 매긴 Item이 무엇인지 알려주고 있다.

1.3. Factorizaion Machines 본문

A. Factorization Machine Model

2차 모델 방정식은 아래와 같다.

$V$ 내부의 행 $v_i$는 k개의 factor를 지닌 i번째 변수를 설명한다. k는 0을 포함한 자연수이며, factorization의 차원을 정의하는 하이퍼 파라미터이다. 2-way FM(2차수)은 변수간의 단일 예측변수와 결과변수 간의 상호작용 뿐 아니라 pairwise한(한 쌍의) 예측변수 조합과 결과변수 사이의 상호작용도 잡아낸다.

부가적으로 설명을 하면,

• $x_i$: X 데이터 셋의 하나의 행 벡터(feature vector)
• $w_0$: global bias
• $w_i$: i번째 변수의 영향력을 모델화 함
• $\hat{w}_{i, j}$ = $<v_i, v_j>$: i, j번째 변수간의 상호작용을 모델화 함
• $v$ 벡터: factor vector

FM 모델은 각 상호작용에 대해 $w_{i, j}$라는 모델 파라미터를 그대로 사용하는 것이 아니라, 이를 factorize하여 사용한다. 나중에 확인하겠지만, 이 부분이 희소한 데이터임에도 불구하고 고차원의 상호작용에 대한 훌륭한 파라미터 추정치를 산출할 수 있는 중요한 역할을 하게 된다.

k가 충분히 크면 positive definite 행렬 W에 대하여 $W = V \bullet V^t$을 만족시키는 행렬 $V$는 반드시 존재한다. 이는 FM모델이 k가 충분히 크면 어떠한 상호작용 행렬 $W$도 표현할 수 있음을 나타낸다. 그러나 sparse한 데이터 환경에서는, 복잡한 상호작용 W를 추정하기 위한 충분한 데이터가 없기에 작은 k를 선택할 수 밖에 없는 경우가 많다.

위 그림을 보면 알 수 있듯이, x벡터 하나당 1개의 예측 값을 산출하게 된다.

참고로, 본 논문에서는 위 그림의 p 대신 n이라고 적혀있는데, 이 p는 예측 변수의 수를 의미하기 때문에, 관례적으로 더 많이 쓰이는 p로 표기한 것이니 착오 없길 바란다.

Sparse한 환경에서, 일반적으로 변수들 간의 상호작용을 직접적이고 독립적으로 추정하기 위한 충분한 데이터가 없는 경우가 많다. FM은 이러한 환경에서도 상호작용들을 추정할 수 있는데, 이는 왜냐하면 이 모델은 상호작용 파라미터들을 factorize하여 상호작용 파라미터들 사이의 독립성을 깰 수 있기 때문이다.

일반적으로 이것은 하나의 상호작용을 위한 데이터가 다른 관계된 상호작용들의 파라미터들을 추정하는 데 도움을 준다는 것읠 의미한다.

앞서 언급했던 예를 들어보자,
Alice와 Star Trek 사이의 상호작용을 추정하여 영화평점(Target y)을 예측하고 싶다고 하자. 당연하게도 학습데이터에는 두 변수 $x_a$와 $x_{ST}$가 모두 0이 아닌 경우는 존재하지 않으므로, direct estimate $w_{A, ST}$는 0이 될 것이다.

그러나 factorized 상호작용 파라미터인 $<V_{A}, V_{ST}>$를 통해 우리는 상호작용을 측정할 수 있다. Bob과 Charlie는 모두 유사한 factor vector $V_B$, $V_C$를 가질 것인데, 이는 두 사람 모두 Star Wars ($V_{SW}$)와 관련하여 유사한 상호작용을 갖고 있기 때문이다. (취향이 비슷하다.) 즉, $<V_{B}, V_{SW}>$과 $<V_{C}, V_{SW}>$가 유사하다는 뜻이다.

Alice($V_A$)는 평점 예측에 있어서 Titanic과 Star Wars 두 factor와 상호작용이 다르기 때문에 Charlie와는 다른 factor vector를 가질 것이다. Bob은 Star Wars와 Star Trek에 대해 유사한 상호작용을 가졌기 때문에 Star Trek과 Star Wars의 factor vector는 유사할 가능성이 높다. 즉, Alice와 Star Treck의 factor vector의 내적은 Alice와 Star Wars의 factor vector의 내적 값과 매우 유사할 것이다. (직관적으로 말이 된다.)

이제 계산적 측면에서 모델을 바라볼 것이다. 앞서 확인한 방정식의 계산 복잡성은 $O(kp^2)$이지만, 이를 다시 변형하여 선형적으로 계산 시간을 줄일 수 있다. pairwise 상호작용 부분은 아래와 같이 재표현할 수 있다.

이 부분이 굉장히 중요한데, 실제로 코드로 구현할 때 이와 같은 재표현 방식이 없다면 굉장히 난감한 상황에 맞닥드리게 될 것이다.

또한 x의 대부분의 원소가 0이므로 실제로는 0이 아닌 원소들에 대해서만 계산이 수행된다.

B. Factorizaion Machine as Predictors

FM은 회귀, 이항 분류, 랭킹 문제를 풀기 위해 활용될 수 있다. 그리고 이 모든 문제에서 L2 정규화 항은 과대적합을 막기 위해 추가된다.

C. Learning Factorizatino Machines

앞서 확인한 것처럼, FM은 선형적으로 계산되는 모델 방정식을 지니고 있다. 따라서 $w_0, w, V$와 같은 모델 파라미터들은 Gradient Descent 방법을 통해 효과적으로 학습될 수 있다. FM 모델의 Gradient는 아래와 같이 표현될 수 있다.

$\sum_{j=1}^n v_{j, f} x_j$는 i에 대해 독립적이기 때문에 우선적으로 미리 계산될 수 있다. 일반적으로 각각의 Gradient는 상수적 시간 O(1)만에 계산될 수 있다. 그리고 (x, y)를 위한 모든 파라미터 업데이터는 희소한 환경에서 $O(kp)$ 안에 이루어질 수 있다.

우리는 element-wise하거나 pairwise한 Loss를 계산하기 위해 SGD를 사용하는 일반적인 implementation인 LIBFM2를 제공한다.

D. d-way Factorizatino Machine

2-way FM은 쉽게 d-way FM으로 확장할 수 있다.

E. Summary

FM 모델은 모든 상호작용을 있는 그대로 사용하는 것이 아니라 factorized 상호작용을 이용하여 피쳐 벡터 x의 값 사이에 있는 가능한 상호작용들을 모델화한다. 이러한 방식은 2가지 장점을 지닌다.

1) 아무리 희소한 환경에서도 값들 사이의 상호작용을 추정할 수 있다. 또한 이는 관측되지 않은 상호작용을 일반화하는 것도 가능하게 한다.
2) 학습 및 예측에 소요되는 시간이 선형적이고, 이에 따라 파라미터의 수도 선형적이다. 이는 SGD를 이용하여 다양한 Loss Function들을 최적화하는 것을 가능하게 한다.

(후략)

2. Tensorflow를 활용한 구현

2.1. 준비

# FM
import numpy as np
import pandas as pd
import tensorflow as tf
from tensorflow.keras.metrics import BinaryAccuracy
from sklearn.preprocessing import MinMaxScaler
from sklearn.model_selection import train_test_split

# GPU 확인
tf.config.list_physical_devices('GPU')

# 자료형 선언
tf.keras.backend.set_floatx('float32')

# 데이터 로드
scaler = MinMaxScaler()
file = load_breast_cancer()
X, Y = file['data'], file['target']
X = scaler.fit_transform(X)

n = X.shape[0]
p = X.shape[1]
k = 10
batch_size = 8
epochs = 10

데이터는 sklearn에 내장되어 있는 breast_cancer 데이터를 사용하였다. 30개의 변수를 바탕으로 암 발생 여부를 예측하는 데이터이다. p는 예측 변수의 개수이고, k는 잠재 변수의 개수이다.

2.2. FM 모델 선언

class FM(tf.keras.Model):
    def __init__(self):
        super(FM, self).__init__()

        # 모델의 파라미터 정의
        self.w_0 = tf.Variable([0.0])
        self.w = tf.Variable(tf.zeros([p]))
        self.V = tf.Variable(tf.random.normal(shape=(p, k)))

    def call(self, inputs):
        linear_terms = tf.reduce_sum(tf.math.multiply(self.w, inputs), axis=1)

        interactions = 0.5 * tf.reduce_sum(
            tf.math.pow(tf.matmul(inputs, self.V), 2)
            - tf.matmul(tf.math.pow(inputs, 2), tf.math.pow(self.V, 2)),
            1,
            keepdims=False
        )

        y_hat = tf.math.sigmoid(self.w_0 + linear_terms + interactions)

        return y_hat

모델 자체는 아주 복잡할 것은 없다. linear terms와 interactions라고 정의한 부분이 아래 수식의 밑줄 친 부분에 해당한다.

interactions 부분이 아주 중요한데, 이 부분을 어떻게 구현하느냐가 속도의 차이를 만들어 낼 수 있기 때문이다. 논문에서는 아래와 같이 이 상호작용 항을 재표현할 수 있다고 하였다.

위 interactions 부분은 위 식을 코드로 표현한 것인데, $\sum$ 항을 벡터화 하여 구현하였다.

설명을 위해, (k=2, p=3) shape을 가진 $V$ 행렬과 (p=3, 1)의 shape을 가진 $x$ 벡터가 있다고 하자. 사실 $(\sum_{i=1}^n v_{i,f } x_i)^2$ 부분을 계산하면 $V^T x$의 모든 원소를 더한 것과 동일하다.

위 그림의 결과는 $(v_{11}x_1 + v_{21}x_2 + v_{31}x_3)^2 + (v_{12}x_1 + v_{22}x_2 + v_{32}x_3)^2$와 동일할 것이다. 식의 나머지 부분도 같은 방법으로 생각하면 위와 같은 코드로 표현할 수 있을 것이다.

2.1.3. 학습 코드

# Forward
def train_on_batch(model, optimizer, accuracy, inputs, targets):
    with tf.GradientTape() as tape:
        y_pred = model(inputs)
        loss = tf.keras.losses.binary_crossentropy(from_logits=False,
                                                   y_true=targets,
                                                   y_pred=y_pred)
    
    # loss를 모델의 파라미터로 편미분하여 gradients를 구한다.
    grads = tape.gradient(target=loss, sources=model.trainable_variables)

    # apply_gradients()를 통해 processed gradients를 적용한다.
    optimizer.apply_gradients(zip(grads, model.trainable_variables))

    # accuracy: update할 때마다 정확도는 누적되어 계산된다.
    accuracy.update_state(targets, y_pred)

    return loss


# 반복 학습 함수
def train(epochs):
    X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=0.2, stratify=Y)

    train_ds = tf.data.Dataset.from_tensor_slices(
        (tf.cast(X_train, tf.float32), tf.cast(Y_train, tf.float32))).shuffle(500).batch(8)

    test_ds = tf.data.Dataset.from_tensor_slices(
        (tf.cast(X_test, tf.float32), tf.cast(Y_test, tf.float32))).shuffle(200).batch(8)

    model = FM()
    optimizer = tf.keras.optimizers.SGD(learning_rate=0.01)
    accuracy = BinaryAccuracy(threshold=0.5)
    loss_history = []

    for i in range(epochs):
      for x, y in train_ds:
          loss = train_on_batch(model, optimizer, accuracy, x, y)
          loss_history.append(loss)

      if i % 2== 0:
          print("스텝 {:03d}에서 누적 평균 손실: {:.4f}".format(i, np.mean(loss_history)))
          print("스텝 {:03d}에서 누적 정확도: {:.4f}".format(i, accuracy.result().numpy()))


    test_accuracy = BinaryAccuracy(threshold=0.5)
    for x, y in test_ds:
        y_pred = model(x)
        test_accuracy.update_state(y, y_pred)

    print("테스트 정확도: {:.4f}".format(test_accuracy.result().numpy()))

epochs = 50으로 실행한 결과는 아래와 같다.

스텝 000에서 누적 평균 손실: 1.2317
스텝 000에서 누적 train 정확도: 0.5692
스텝 002에서 누적 평균 손실: 0.9909
스텝 002에서 누적 train 정확도: 0.6271

...

스텝 048에서 누적 평균 손실: 0.2996
스텝 048에서 누적 train 정확도: 0.8996

테스트 정확도: 0.9500

Reference

http://nowave.it/factorization-machines-with-tensorflow.html