Python 프로젝트 생성하기
18 Jul 2022 | 파이썬이번 글에서는 새로운 파이썬 프로젝트를 진행하기 위한 환경을 쉽고 빠르게 구축하는 방법에 대해 서술해보겠습니다.
본 글은 윈도우를 기준으로 설명합니다.
Python 프로젝트 생성하기
1. Poetry 설명
poetry는 의존성 관리와 빌드를 책임지는 라이브러리입니다.
poetry를 설치한 후, 아래 명령어를 입력합니다.
# 새로운 프로젝트를 만들 경우
poetry new my-project
# 기존 프로젝트를 활용할 경우
poetry init
이제 pyproject.toml 파일이 생성되었을 것입니다.
새로 가상 환경을 만든다고 할 때, 프로젝트의 root directory 아래에 virtualenv 가 있는 것이 편합니다. 만약 새로 만드는 것이 싫다면 아래와 같이 설정합니다.
poetry config virtualenvs.create false # 기본 값은 true
이 링크를 참조하셔도 좋습니다.
프로젝트 내부에 .venv 폴더를 생성하는 옵션은 아래와 같습니다.
poetry config virtualenvs.in-project true # 기본 값은 None
의존성은 위 파일의 [tool.poetry.dependencies]와 [tool.poetry.dev-dependencies]에서 관리하고 있습니다. add 서브 커맨드를 통해 의존성을 추가할 수 있습니다.
poetry add numpy
이 때 poetry.lock 파일이 생성됩니다.
다음 명령어를 실행하면 전체적으로 업데이트가 가능합니다.
poetry update
현재 프로젝트의 pyproject.toml 파일을 읽어 의존성 패키지를 실행하고 싶을 때는 아래 명령어를 실행합니다.
poetry install
설치된 패키지 목록은 show를 통해 알아 볼 수 있습니다.
# 설치된 모든 패키지
poetry show
# 개발환경용은 제외
poetry show --no-dev
# 세부 내용
poetry show django
# 최신 버전
poetry show --latest (-l)
# 업데이트가 필요한 패키지
poetry show --outdate (-o)
# 의존성 트리
poetry show --tree
가상 환경에 대한 정보는 아래 명령어로 확인할 수 있습니다.
# 가상 환경 정보 확인
poetry env info
# 가상환경 리스트 확인
poetry env list
2. Github Action 설명
Github Action은 github에서 제공하는 CI/CD 도구이며, 소프트웨어 개발의 workflow를 자동화해줍니다.
Github Action에는 반드시 알아야 할 개념들이 있습니다. 이 문서를 확인하는 것이 가장 정확합니다.
가장 기본적인 설명은 이러합니다.
PR 생성과 같이 repository에 특정 event가 발생하면 트리거되는 Github Action workflow를 구성할 수 있습니다. workflow는 순차적 혹은 병렬적으로 동작하는 1개 이상의 job을 갖고 있습니다. 각각의 job은 할당된 가상 머신 runner 내부 혹은 container 내부에서 동작하며 action 혹은 script를 실행하도록 되어 있습니다.

workflow
- 1개 이상의 job을 실행시키는 자동화된 프로세스
- yaml 파일로 정의함
- repository 내에 .github/workflows 디렉토리 안에서 정의됨
- 하나의 repository는 복수의 workflow를 정의할 수 있음
events
- workflow run을 트리거하는 특정 행동
jobs
- 동일한 runner 내에서 실행되는 여러 step
- 각 step은 shell script이거나 동작할 action
action
- workflow의 가장 작은 블록
- 재사용이 가능한 component
runner
- github action runner 어플리케이션이 설치된 머신
- workflow가 실행될 인스턴스
action 개념에 대해 추가 설명이 필요하다면 이 블로그를 참고하셔도 좋겠습니다.
이제 실제로 workflow를 작성해 보겠습니다. 앞서 소개한 여기를 참고해주세요. workflow 구문에 대해 자세히 알고 싶다면 여기를 참고하면 됩니다.
workflow는 yaml 파일에 기반하여 구성됩니다. name은 workflow의 이름을 의미하며, 이 name이 repository의 action 페이지에 표시될 것입니다. on은 workflow가 작동하도록 트리거하는 event를 정의합니다. 대표적으로 push, pull_request 등을 생각해 볼 수 있을 텐데, 모든 조건에 대해 알고 싶다면 여기를 확인해 주세요.
특정 event의 경우 filter가 필요한 경우가 있습니다. 예를 들어 push가 어떤 branch에 발생했는지에 따라 트리거하고 싶을 수도 있고 아닐 수도 있습니다. 공식 문서의 설명은 여기에 있습니다.
지금까지 설명한 내용의 예시는 아래와 같습니다.
name: CI
on:
pull_request:
branches: [main]
이제 job을 정의해 보겠습니다. 복수의 job을 정의할 경우 기본적으로 병렬 동작하게 됩니다. 따라서 순차적으로 실행되길 원한다면 반드시 jobs.<job_id>.needs 키워드를 통해 의존 관계를 정의해야 합니다. 각 job은 runs-on으로 명시된 runner environment에서 실행됩니다. environment에 대해서는 여기를 확인하면 됩니다.
아래 예시에서 my_first_job과 my_second_job이 job_id에 해당한다는 점을 알아두세요. My first job과 My second job은 jobs.<job_id>.name (name) 이며 github UI에 표시됩니다.
jobs:
my_first_job:
name: My first job
my_second_job:
name: My second job
needs를 통해 반드시 이전 job이 성공적으로 끝나야만 다음 job이 실행되도록 정의할 수 있습니다. 물론 조건을 추가해서 꼭 성공하지 않더라도 실행되도록 작성할 수도 있습니다.
jobs:
job1:
job2:
needs: job1
job3:
needs: [job1, job2]
앞서 job 내에는 연속된 task로 구성된 steps가 존재한다고 설명했습니다. jobs.<job_id>.steps는 명령어를 실행하거나 setup task를 수행하거나 특정한 action을 실행할 수 있습니다.
steps 아래에 if 조건을 추가하게 되면 반드시 이전의 조건이 만족되어야 연속적으로 실행되도록 만들 수 있습니다. context를 이용한다면 아래 예시를 보면 됩니다.
steps:
- name: My first step
if: $
run: echo This event is a pull request that had an assignee removed.
status check function을 이용해 보겠습니다. My backup step이라는 task는 오직 이전 task가 실패해야만 실행될 것입니다.
steps:
- name: My first step
uses: octo-org/action-name@main
- name: My backup step
if: $
uses: actions/heroku@1.0.0
steps의 구성 요소를 좀 더 살펴보겠습니다. jobs.<job_id>.steps[*].name은 github UI에 표시될 name을 의미합니다.
jobs.<job_id>.steps[*].uses는 어떠한 action을 실행할지를 의미합니다. 이는 같은 repository나 public repository 혹은 published docker container image에서 정의될 수 있습니다.
다양한 예시가 존재합니다. versioned action, public action, public action in a subdirectory, same repository 내의 action 및 docker hub action 등을 이용할 수 있습니다. 이에 대한 공식 문서 설명은 여기를 확인해 주세요.
여러 action 중 가장 많이 사용되는 action은 checkout인데, repository로부터 코드를 다운로드 받기 위해 사용됩니다. 이 checkout을 github action의 입장에서 바라보면 github의 repository에 올려 둔 코드를 CI 서버로 내려받은 후 특정 branch로 전환하는 작업으로 이해할 수 있다고 합니다. (참고 블로그 인용) 실제로 이 action을 직접 수행하려면 번거로운 작업들이 선행되어야 하지만, github action은 이를 편하게 묶어서 action으로 제공하고 있습니다.
workflow yaml 파일에서 steps.uses 키워드에 사용하고자 하는 action의 위치를 {소유자}/{저장소명}@참조자 형태로 명시해야 한다고 합니다. 예시는 아래와 같습니다.
steps:
- name: Checkout
uses: actions/checkout@v3
내부적으로는 git init/config/fetch/checkout/log 등의 명령어를 수행한다고 합니다. 가장 최신 버전의 checkout action에 대해서는 이 repository에서 확인할 수 있습니다.
python으로 개발을 하는 사용자라면 파이썬을 설치하는 setup-python 또한 자주 사용하게 될 것입니다. repo는 여기입니다. 이 action을 통해 CI 서버에 python을 설치할 수 있으며 특정 버전이 필요할 경우 아래와 같이 작성하면 됩니다.
steps:
- name: Set up Python
uses: actions/setup-python@v3
with:
python-version: 3.9
jobs.<job_id>.steps[*].run은 운영체제의 shell을 이용하여 command-line 프로그램을 실행시킨다. 아래와 같이 single-line command를 입력할 수도 있고,
- name: Install Dependencies
run: npm install
multi-line command로 입력할 수도 있습니다.
- name: Clean install dependencies and build
run: |
npm ci
npm run build
예시는 여기를 참고해 주세요. 파이썬 스크립트 예시 하나는 기록해 둡니다.
steps:
- name: Display the path
run: |
import os
print(os.environ['PATH'])
shell: python
jobs.<job_id>.steps[*].with는 action에 의해 정의된 input 파라미터들의 map을 의밓바니다. 각 input 파라미터는 key/valu 쌍으로 이루어져있으며, input 파라미터들은 환경 변수들의 집합에 해당합니다.
그 외에도 steps 아래에는 args, entrypoint, env 등 여러 속성을 정의할 수 있습니다.
3. 정리
이번 chapter에서는 위 내용과 더불어 publishing까지 전체 flow 진행에 대해 알아보겠습니다.
pycharm을 이용한다면 다음과 같이 처음부터 poetry를 이용해서 편리하게 프로젝트를 시작할 수 있습니다.
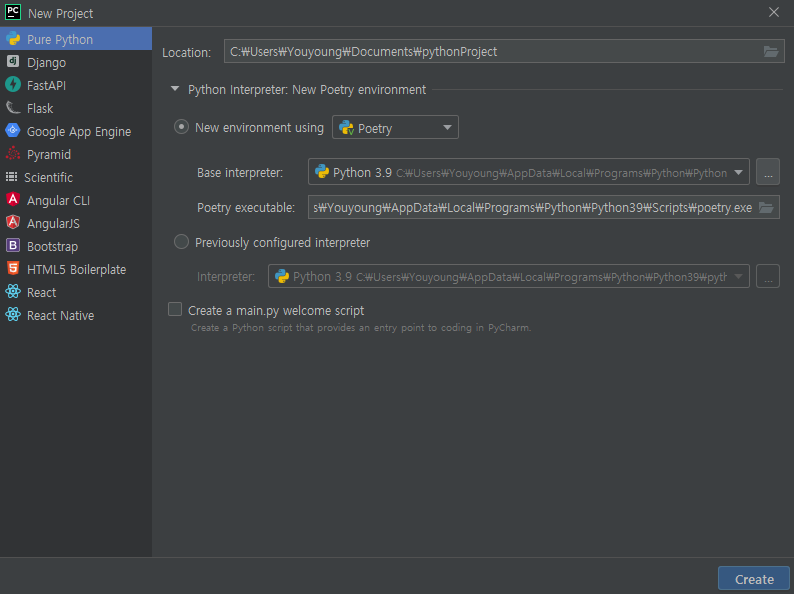
이전에 init 을 통해 생성되었던 poetry.lock 및 pyproject.toml 파일이 생성되었을 것입니다.
사용하는 library 들을 poetry add {library} 를 통해 추가해줍니다.
이제 github action을 이용하여 CI/CD 환경을 구축해줄 차례입니다. 아래와 같이 .github 디렉토리 아래에 2개의 yaml 파일을 생성해 줍니다.
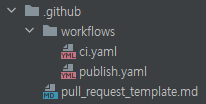
먼저 CI 부분부터 살펴보겠습니다. 아래는 ci.yaml 파일의 예시입니다.
name: CI
on:
pull_request:
branches: [main]
jobs:
ci-test:
name: ci-test
runs-on: windows-latest
steps:
- name: Checkout
uses: actions/checkout@v3
- name: Set up Python
uses: actions/setup-python@v3
with:
python-version: 3.9
- name: Install dev-dependencies
run: pip3 install -r requirements-dev.txt
- name: Lint
run: make check
조건은 간단합니다. main branch에 PR이 생성되었을 경우 make check 명령문을 실행하게 됩니다. 이 부분은 아래와 같이 작성하였습니다.
(pylint, isort, black 모두 poetry add를 통해 의존성 추가를 해주어야 합니다.)
.PHONY: init format check requirements
init:
pip install poetry
poetry install
format:
isort --profile black -l 119 {library} lint.py
black -S -l 119 {library} lint.py
check:
isort --check-only --profile black -l 119 {library}
black -S -l 119 --check {library}
requirements:
poetry export -f requirements.txt -o requirements.txt --without-hashes
poetry export --dev -f requirements.txt -o requirements-dev.txt --without-hashes
참고로 Windows 환경에서 Makefile을 작성하기 위한 방법은 이 곳에 잘 설명되어 있습니다.
위 파일 작성을 마쳤다면, PR을 생성하기 이전에 코드 정리가 잘 되어 있는지, requirements 파일은 생성했는지 확인해 주면 됩니다.
PR이 closed 되었을 때, CD 구조가 진행되도록 해보겠습니다. 아래는 publish.yaml 파일의 예시입니다.
name: PUBLISH LIBRARY
on:
pull_request:
branches: [main]
types: [closed]
jobs:
build:
name: build-library
runs-on: windows-latest
steps:
- name: Checkout
uses: actions/checkout@v3
- name: Set up Python
uses: actions/setup-python@v3
with:
python-version: 3.9
- name: Install requirements
run: pip3 install poetry
- name: Bump version
run: poetry version patch
- name: Publish library
env:
PYPI_TOKEN: $
run: |
poetry build
poetry publish --username $ --password $
Install requirements 까지는 추가적인 설명이 필요하지 않아 보입니다.
Bump version은 패키징하고자 하는 library의 version을 자동적으로 upgrade하는 부분입니다. library를 0.1.0에서 0.1.1로 올릴지, 0.2.0으로 올릴지, 1.0.0으로 올릴지 선택할 수 있습니다.
이 곳을 참고하면 자세한 정보를 확인할 수 있습니다.
다음은 여러 token을 읽고 build -> publish까지 이어지는 부분입니다. 일단 secrets가 무엇인지부터 확인해 보겠습니다. github repository의 Actions Secrets은 환경 변수를 암호화해서 저장할 수 있는 기능입니다. Settings-Security-Secrets를 통해 접근할 수 있습니다.
PYPI 홈페이지에서 본인의 repository에서 사용할 token을 추가해줍니다. 그리고 생성한 값을 복사한 뒤, PYPI_TOKEN secrets에 저장해줍니다. 마찬가지로 PYPI_USERNAME과 PYPI_PASSWORD도 추가해줍니다.
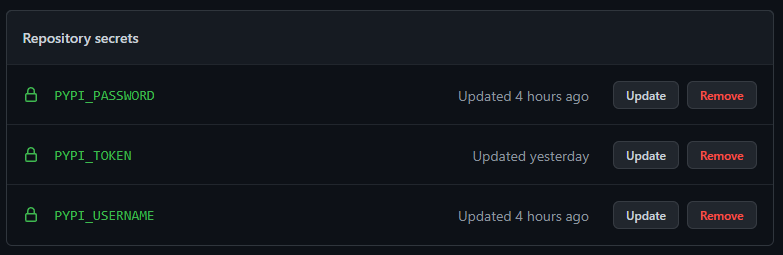
이렇게 추가된 token들은 인증과정에 사용됩니다.
이제 CI/CD 구축은 끝났습니다. library 코드를 정리하고, PR 과정을 정상적으로 거치면 프로젝트 생성부터 패키징, 배포까지 편리하게 진행할 수 있습니다.