이번 포스팅에서는 AB Test를 진행할 때 거의 필수적으로 고려해야 하는 Sample Size를 구하는 과정에 대해 정리해본다.

AB Test Sample Size 구하기

1. Basic

귀무가설과 대립가설이 아래와 같다고 해보자.

[H_0: \mu = \mu_0]

[H_a: \mu > \mu_0]

실험의 특성을 고려하여 유의수준과 검정력을 설정하면 이를 통해 최소 Sample Size를 추정할 수 있다. 1 - 검정력인 $\beta$ 는 $\mu = \mu_a$, \mu_a > \mu_0$ 과 같이 $\mu$ 를 특정 값으로 지정하였을 때 구할 수 있다.

Reject Region(기각역)이 아래와 같이 정의된다고 하자. $\hat{\theta}$ 는 물론 추정량을 의미한다.

[RR = { \hat{\theta}: \hat{\theta} > k }]

$k$ 는 기각역이 시작되는 point이다.

2종 오류가 발생할 확률인 $\beta$ 는 대립가설이 참일 때 귀무가설을 적절히 기각하지 않을 확률을 의미한다. 이를 위 수식과 이어서 설명하면, 아래와 같이 표현할 수 있다.

[\beta = P(\hat{\theta} \leq k, \theta = \theta_a)]

위 사실들을 고려하여 다시 한 번 $\alpha$ 와 $\beta$ 를 구해보자.

[\alpha = P(\bar{Y} > k, \mu = \mu_0)]

[= P( \frac{\bar{Y} - \mu_0}{\sigma / \sqrt{n}} > \frac{k - \mu_0}{\sigma / \sqrt{n}}, \mu = \mu_0 )]

[= P(Z > \mathcal{z}_{\alpha})]

[\beta = P(\bar{Y} \leq k, \mu = \mu_a)]

[= P( \frac{\bar{Y} - \mu_a}{\sigma / \sqrt{n}} \leq \frac{k - \mu_a}{\sigma / \sqrt{n}}, \mu = \mu_a )]

[= P(Z \leq - \mathcal{z}_{\beta})]

위 2개 식에서 우리는 아래 사실들을 정리할 수 있다.

[\frac{k - \mu_0}{\sigma / \sqrt{n}} = \mathcal{z}_{\alpha}]

[\frac{k - \mu_a}{\sigma / \sqrt{n}} = -\mathcal{z}_{\beta}]

위 식을 $k$ 에 대해 정리하면 다음과 같다.

[k = \mu_0 + \mathcal{z}{\alpha} (\frac{\sigma}{\sqrt{n}}) = \mu_a - \mathcal{z}{\beta} (\frac{\sigma}{\sqrt{n}})]

따라서 위 식에서 $k$ 를 제외하고 $n$ 에 대해 다시 정리하면, Sample Size for an Upper-tail $\alpha$ - level Test를 얻을 수 있다.

[n = \frac{(\mathcal{z}{\alpha} + \mathcal{z}{\beta})^2 \sigma^2}{(\mu_a - \mu_0)^2}]

이 때 분모에서 제곱항 내부에 위치한 값을 Effect Size라고 표현하며, 실험에서 확인하고 싶은 유의미한 차이를 의미한다.

[\delta = \mu_a - \mu_0]

그리고 위 공식은 $n$ 이 충분히 클 때 성립한다.

2. Proportion Test

애플리케이션 상에서 AB Test를 할 때에는 비율의 차이를 metric으로 두는 경우가 많다. 예를 들어 새로운 모델을 배포하였을 때 Conversion Rate이 충분히 상승하였는지 알고 싶을 수 있다. 이 경우 귀무가설과 대립가설은 아래와 같다.

[H_0: p = p_0]

[H_a: p > p_0]

이 경우도 결국 똑같이 구할 수 있다. 신청 여부에 따른 분포이기 때문에 본 Test에서는 이항 분포가 사용된다. 그렇다면 분산은 아래와 같이 구할 수 있다.

[\sigma_0^2 = p_0 (1-p_0)]

새로운 모델에서의 목표 Conversion Rate을 $p_a$ 라고 하면 Effect Size는 $p_a - p_0$ 가 될 것이다. 그리고 표본 평균의 분산은 아래와 같이 구할 수 있다.

[\sigma^2 = p_0(1-p_0) + p_a(1-p_a)]

위 사실을 모두 종합하여 Sample Size를 구해보면 다음과 같다.

[n = \frac{(\mathcal{z}{\alpha} + \mathcal{z}{\beta})^2 (p_0(1-p_0) + p_a(1-p_a)) }{(p_a - p_0)^2}]

만약 아래와 같은 실험 설정이라면,

[\alpha = 0.05, 1 - \beta = 0.8, p_0 = 0.02, p_a = 0.022]

필요한 최소 Sample Size는 63215이다.

References

1) Mathematical Statistics with Applications(Denis D. Wackerly, …) Ch 10.4
2) Comparing Two Proportions – Sample Size

이번 포스팅에서는 AB Test에 대해 정리해본다. 사실 AB Test를 완벽히 설명하기 위해서는 정말 많은 자료와 깊은 고민의 경험이 필요하다. 본 글은 단지 필자가 생각을 정리하기 위해 작성한 글임을 밝혀둔다.

AB Test 기본

1. Background

AB Test는 간단히 말해서 User를 무작위로 2개의 그룹으로 구분한 뒤, 서로 다른 Action을 수행했을 때의 반응의 차이를 파악하는 분석 기법이다. Bayesian AB Test를 사용할 수도 있지만, 일반적으로는 Frequentist AB Test 관점이 더욱 자주 사용되는 것으로 보인다.

Null Hypothesis를 $H_0$, Alternative Hypothesis를 $H_1$ 이라고 한다면, 일반적으로 우리의 목표는 Null Hypothesis(귀무가설)를 기각하는 것이 된다. 만약 기각하지 못할 경우 우리는 귀무가설을 기각할 충분한 근거가 없다고 판단내려야 한다.

1종 오류는 귀무가설이 True임에도 우리가 실험을 통해 이를 기각하는 오류를 의미하며 $\alpha$ 라고 표기한다. 2종 오류는 반대로 귀무가설이 False임에도 우리가 이를 기각하지 않는 오류를 의미하며 $\beta$ 라고 표기한다. 그리고 귀무가설이 False인데 우리가 이를 잘 기각할 확률을 의미하는 검정력은 $1-\beta$ 로 계산한다.

이러한 가설을 기각할 것인가를 판단하는 기준으로 우리는 P-value를 사용하게 된다. P-value는 간단히 말해서 귀무가설 $H_0$ 이 True라고 가정하고 얻은 확률 분포에서 현재의 실험 결과가 나올 확률을 의미한다. 만약 이렇게 얻은 P-value가 0.01이라고 하면, 귀무가설이 True일 때 현재의 결과가 나올 확률이 1%란 이야기이므로, 우리가 일반적으로 사용하는 유의수준 0.05보다 한참 낮은 값이다. 따라서 보통 이 경우 귀무가설을 기각하고, 통계적으로 유의미한 차이가 있다고 결론 내리게 된다.

2. Netflix: What is an A/B Test?

이번 장에서는 AB Test에 대해 쉽게 풀어쓴 Netflix의 게시물을 소개한다. 원문 링크는 글 하단에 있는 참고 문헌 목록에서 확인할 수 있다.

위와 같이 2개의 선택지를 놓고 어떤 방식이 더 우수한 결과를 이끌어내는지 확인해 볼 수 있다. 좌측에 위치한 선택지가 기존 방식이라고 하면 이 방식의 UI를 경험할 고객 군을 Control Group이라고 지칭한다. 반면 새로운 선택지, 즉 우측에 위치한 방식의 UI를 경험할 고객 군은 Treatment Group이라고 한다.

위 사례 처럼 UI 관련 실험에서는 여러 변인들에 대해서도 살펴보아야 한다. 예를 들어 앱을 로딩하는데 시간이 더 걸린다거나, 네트워크 상태에 따라 영상의 질이 변하는 것은 아닌지 등을 반드시 체크해야 한다.

실험의 성과를 결정할 지표(metric)이 결정되었다면, 이 지표가 무엇을 의미하는지 명확히 파악해야 한다. 예를 들어 CTR을 metric으로 정했다고 하자. 단순히 CTR이 높다고 좋은 일일까? 어떤 고객들은 뒤집힌 영화의 제목을 보면서 제대로 보기 위해 컨텐츠를 클릭했을 수도 있다. 단순히 CTR이 높다고 좋은 실험이었다고 결론을 내려버리면 서비스를 제대로 이해하지 못한 것이라고 할 수 있다.

Netflix에서는 고객에게 주는 만족감을 더욱 잘 포착할 수 있는 일반적인 지표를 본다. 이를 member engagement with Netflix라고 표현할 수 있는데, 결국 이는 고객들이 Netflix를 이용하는 것을 취미로써 계속 선택하고 있는지에 관한 문제이다.

Holding everything else constant
무작위 추출로 2개의 그룹을 추출하였다 하더라도, 성과에 큰 영향을 줄 수 있는 여러 변인에 대한 점검은 필수적이다. Netflix에서는 멤버십의 길이, 컨텐츠의 선호도, 언어 등과 같은 요소들을 예시로 들고 있다. 오직 테스트하고자 하는 그 변수 하나만 달라야 한다.

It all starts with and idea
Netflix에서는 AB Test는 하나의 아이디어에서 출발한다고 강조하고 있다. 그것이 UI에 대한 변화일 수도 있고, 개인화 시스템이 될 수도 있고 가입 절차의 변화가 될 수도 있다. 이제는 익숙한 Top10 컨텐츠도 처음에는 테스트 가설에서 시작했다고 한다. 이 아이디어에서 얻고자 했던 것은 2가지이다. popular 컨텐츠를 소개함으로써 보는 이로 하여금 공유된 경험을 느끼게 만들고자 했던 것이 첫 번째 목표이고, 다른 사람들이 자주 보는 컨텐츠를 같이 향유함으로써 같은 주제로 다른 사람들과 대화하고 싶어하는 인간의 내재된 욕망을 이끌어 내는 것이 두 번째 목표였다고 한다.

특히 2번째 목표가 인상적인데, 주위를 슬쩍 둘러봐도 Netflix에서 히트작이 나오면 그 작품에 대해 이야기를 주고 받는 사람들을 자주 목격할 수 있다.

그렇다면 이 가설이 맞다는 것을 어떻게 증명했을까? 메인 지표로는 멤버십 구독이 설정되었는데 왜냐하면 이것이 결국 engagement with Netflix과 큰 상관 관계가 있기 때문이다. 그 외에도 Top10 목록에 나타난 제목 및 다른 부분에 대한 viewing과 같은 보조 지표 역시 검증의 기준으로 활용되었다.

마지막으로 모든 아이디어가 성공으로 이어지는 것이 아니기 때문에 일종의 guardrail이 설정되었다. 실험 역시 중요하지만 이것이 고객 경험의 질의 악화로 이어져서는 안된다. 따라서 실험 때문에 Treatment Group에 있는 고객들이 비정상적으로 서비스 센터로 연락을 더 많이 한다거나 하는 현상이 발생하면 이를 확인하여 조치하도록 하였다.

본 글을 통해 Netflix의 AB Test 철학에 대해 알 수 있었다.

3. 생각할 수 있는 문제점

다시 기본 주제로 돌아온다. 1장에서 설명한 수준으로 AB Test를 진행하고 의사 결정을 내린다면 운이 따르지 않을 경우 좋지 않은 결과를 떠안아야 할 수도 있다. 본 Chapter에서는 AB Test에서 발생할 수 있는 여러가지 문제점에 대해 짚어보고 해결책에 대해 논의한다. Reference에 링크를 첨부한 여러 블로그와 Medium에 있는 Tech Company의 포스팅 및 몇 가지 교재를 참조하였음을 밝힌다.

일단 첫 번째로 생각할 수 있는 부분은 유의 수준에 관한 것이다. 0.05라는 수치는 적절한 것일까? 이 부분에 대해서는 꽤 많은 챌린지가 발생했으며 일부 통계학자들은 0.05 대신 최소한 0.005 수준의 P-value를 고려하는 것이 적절하다고 이야기하고 있다.

그 다음으로는 실험 기간과 표본 수에 대해 생각해볼 수 있다. 실험 결과에서 같은 수준의 차이를 보였다 하더라도, 더 오랫동안 실험하거나, 더 많은 수의 표본을 모으면 표본 오차가 작아지기 때문에 더 작은 P-value를 얻을 가능성이 높아진다. 실제 서비스에서 AB Test를 실행한다고 하면 이 또한 비용이 들어가는 것이므로 실험 기간에 대해서는 신중해질 수 밖에 없다. 따라서 무작정 더 오래 실험해야 합니다! 라고 이야기할 수는 없는 것이다.

그래서 반드시 고려되어야 할 부분이 바로 Effect Size이다. P-value는 표본의 크기가 커질 때도 작아지지만 Effect Size가 커질 때도 작아진다. Effect Size의 수치 자체도 중요하지만, 이 수치가 실제 서비스에서 어느 정도의 의미를 갖는지를 명확히 판단하는 것이 더욱 중요하다.

• 0.1%의 CTR 향상은 성공이라고 말할 수 있는가?
• 이번에 새롭게 모델을 배포했다면 어느 정도의 향상을 기대해야 성공이라고 이야기할 수 있는가?

위와 같은 형식의 질문에 답해보고, 이를 바탕으로 실험 계획을 수립하고 이후의 분석 및 action item 선정 작업을 진행해야 할 것이다.

4. 적절한 실험 규모

목표하는 Effet Size, 1종 오류 및 2종 오류의 수준 등을 모두 고려하면 적절한 실험 규모를 산정할 수 있다. 2가지 오류 모두 고려하는 것이 마냥 쉽지만은 않다. 효과/차이가 없다는 것을 판별하는 것도 중요하고 유의미한 효과가 존재할 때 이를 잘 뒷받침하는 것 또한 놓칠 수 없는 것이 AB Test의 본질이다.

본 내용에 대해서는 더욱 자세한 설명이 필요하므로 추후 다른 글에서 정리해보도록 하겠다.

References

1) 블로그: AB Test에서 p-value에 휘둘리지 않기
2) Netflix: What is an A/B Test?

이번 포스팅에서는 Apache Spark의 기본에 대해 정리해본다. 평소에 자주 사용하지만 정확히 숙지하지 못한 부분들을 정리하는 데에 목적이 있다.

Apache Spark 기본

1. 기본 개념

Spark는 여러 컴퓨터를 모은 클러스터를 관리하는 framework다. 이 때 클러스터는 Hadoop Yarn, Mesos 같은 클러스터 매니저가 관리하게 되며, Spark는 클러스터의 데이터 처리 작업을 관리 및 조율하게 된다.

사용자는 이 클러스터 매니저에 애플리케이션을 제출하고, 클러스터 매니저는 애플리케이션 실행에 필요한 자원을 할당하게 된다.

Spark 애플리케이션은 Driver 프로세스와 다수의 Executor 프로세스로 구성된다. 이 때 Driver 프로세스는 메인 함수를 실행하고, 전반적인 Executor 프로세스의 작업과 관련된 분석, 배포 및 스케쥴링을 담당하게 된다. Executor 프로세스는 Driver 프로세스가 할당한 작업을 수행한 후 다시 보고한다.

즉, 이름에서도 알 수 있듯이 Driver 프로세스는 계획을 수립하고 명령을 내리는 컨트롤 타워의 역할을 하고, Executor 프로세스는 이를 수행하는 일꾼의 역할을 한다는 것을 알 수 있다.

아래 그림은 클러스터 매니저가 물리적 머신을 관리하고 스파크 애플리케이션에 자원을 할당하는 방법을 나타낸다. 사용자는 각 Executor에 할당할 노드 수를 지정할 수 있다.

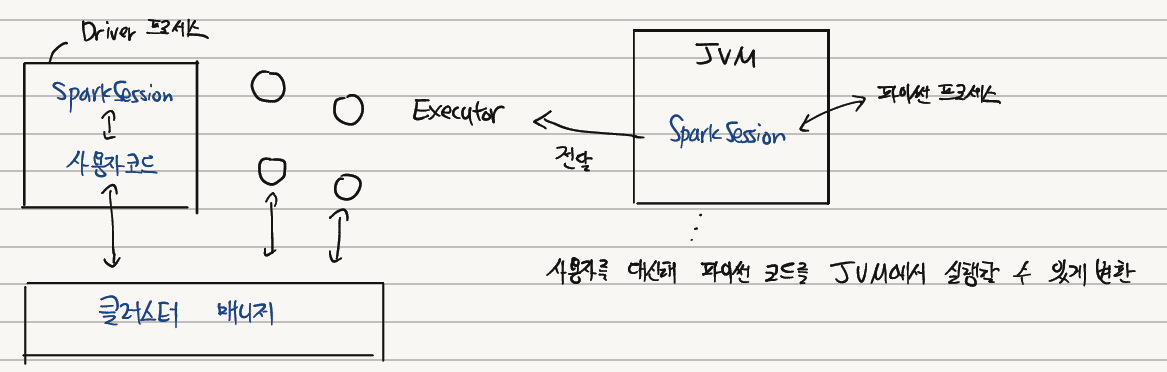
Spark는 파이썬, 자바, 스칼라, R을 지원한다. 예를 들어 파이썬을 사용한다고 하면 Spark는 사용자를 대신하여 파이썬으로 작성한 코드를 Executor의 JVM에서 실행할 수 있는 코드로 변환한다. 이 과정에도 역시 비용이 든다. 따라서 만약 사용자가 큰 비용을 수반하는 UDF를 생성해야 한다면 스칼라나 자바로 이를 구현하는 것이 좀 더 효율적이다.

SparkSession은 앞서 기술한 Driver 프로세스이다. 사용자가 정의한 처리 명령을 클러스터에서 실행하게 되는데, 하나의 SparkSession은 하나의 Spark 애플리케이션에 대응한다.

그리고 SparkSession의 SparkContext는 클러스터에 대한 연결을 나타낸다. 이 SparkContext를 통해 RDD 같은 저수준 API를 사용할 수 있다.

Spark에는 3가지의 구조적 API가 존재한다. DataFrame, Dataset, SparkSQL이 그 대상들이다. 다만 Dataset의 경우 파이썬이나 R에서는 지원되지 않는다. 이들 개념에 대해서는 다음 장에서 살펴본다. Spark DataFrame이나 Dataset은 수 많은 컴퓨터에 분산 저장된다.

파티션은 모든 Executor가 병렬로 작업을 수행할 수 있도록 chunk로 데이터를 분할한 것이다. 파티션은 또한 데이터가 클러스터에서 물리적으로 분산되는 방식을 나타내고, 만약 파티션이 1개면 Executor가 많아도 병렬성은 1이 된다.

기본적으로 DataFrame과 같은 Spark의 핵심 구조는 immutable하고, 변경하고 싶다면 명령을 내려줘야 한다. 이 명령을 Transformation이고, 이 개념은 Spark에서 비즈니스 로직을 표현하는 핵심 개념이다.

Transformation에는 다음과 같이 2종류가 존재하고, Wide Dependency를 가지는 Transformation은 Shuffle 비용을 발생시키기 때문에 주의가 필요하다.

이렇게 만든 Transformation은 바로 실행되는 것은 아니다. 왜냐하면 Spark는 Lazy Execution이라는 규칙을 갖고 있기 때문이다. Spark는 특정 연산 명령이 내려지면 데이터를 즉시 수정하는 것이 아니라 실행 계획을 생성하고, 마지막 순간 전에 원형 Transformation을 간결한 물리적 실행 계획으로 컴파일한다. 그리고 이 과정 속에서 Spark는 사용자가 쉽게 할 수 없는 최적화를 수행하여 작업의 효율성을 높인다.

Action은 실제 연산을 지시하는 명령이다. 예를 들어 count 명령은 DataFrame의 전체 레코드 수를 반환하는 Action이다. 이렇게 Action을 지정하면 Spark Job이 시작된다. 참고로 Spark 애플리케이션은 1개 이상의 Job으로 구성된다.

2. 구조적 API

구조적 API는 데이터 흐름을 정의하는 기본 추상화 개념이고 앞서 언급하였듯이 DataFrame, Dataset, SparkSQL로 구성된다. 구조적 API는 비정형 로그파일부터 정형적인 Parquet 파일까지 다양한 유형의 데이터를 처리할 수 있다.

DataFrame과 Dataset의 공통적인 특성은 다음과 같다.

• 잘 정의된 Row, Column을 갖는 분산 테이블 형태의 컬렉션
• 결과를 생성하기 위해 어떤 데이터에 어떤 연산을 적용해야 하는지 정의하는 지연 연산의 실행 계획
• 불변성을 지님
• DataFrame에 액션을 호출하면 Spark는 Transformation을 실제로 실행하고 결과를 반환함
• DataFrame을 사용하면 Spark의 최적화된 내부 포맷을 이용할 수 있음

마지막 부분이 중요한데, 사실 Spark는 사용자 모르게 (물론 살펴보면 알 수 있다.) 복잡한 연산 과정에 대해 수많은 최적화를 수행한다. 이 때 구조적 API인 DataFrame을 사용하면 Spark의 최적화 과정은 더욱 빛을 발하게 된다. 이는 결국 정확히 어떤 작업을 하는지 인지하고 있을 때만 저수준 API인 RDD를 호출해야 하며, 명확한 목적과 설계가 잡혀있지 않는 이상 웬만하면 DataFrame 수준에서 작업을 진행하는 것이 좋다는 뜻이다.

구조적 API의 실행 과정에 대해 살펴보자.

일단 구조적 API를 이용하여 코드를 작성한다. Spark는 이를 논리적 실행 계획으로 변환한다. 이후 논리적 실행 계획을 물리적 실행 계획으로 변환하며 이 과정에서 최적화를 할 수 있는지 확인한다. 최적화는 Catalyst Optimzer에 의해 이루어진다. Spark는 알아서 실행 과정 속에서 최적화를 해주는 것이다!

이후 Spark는 클러스터에서 물리적 실행 계획, 즉 RDD 처리를 실행한다. 물리적 실행 계획은 일련의 RDD와 Transformation으로 변환되는데, Spark는 구조적 API로 정의된 쿼리를 RDD Transformation으로 컴파일한다. 이 과정 때문에 Spark는 컴파일러로 불린다.

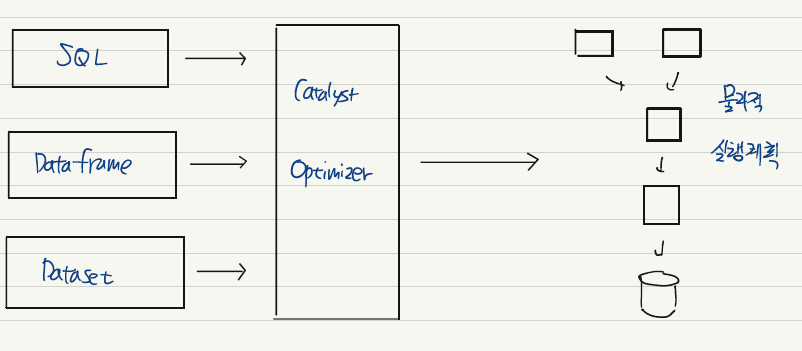
사용자는 DataFrame과 같은 구조적 API에 기반하여 코드를 짜게 될 것이다. 그렇게 하면 이 추상화된 개념을 놓고 Spark는 실제 실행 계획을 수립하면서 최적화를 하고 최종적으로 결과물을 반환하게 된다.

3. 저수준 API

Spark에서는 2가지 저수준 API를 지원한다. 하나는 앞선 장에서 언급한 RDD이다. 다른 하나는 Broadcast 변수와 Accumulator와 같은 분산형 공유 변수를 배포하고 다루기 위한 API이다.

3.1. RDD

RDD는 resilient distributed dataset의 약자로, 다수의 서버에 걸쳐 분산(distributed) 방식으로 저장된 데이터 요소들의 집합을 의미하며, 병렬 처리가 가능하고 장애가 발생해도 스스로 복구 가능(resilient)하다.

Dataset과 DataFrame이 존재하기 전에는 RDD 자체로 많이 사용하였지만 현재는 이 자체로는 특수한 목적 외에는 잘 사용되지는 않는다. 물론 사용자가 작성한 Dataset, DataFrame 코드는 앞서 기술하였듯이 실제로는 RDD로 컴파일되어 수행된다. RDD를 사용하면 Spark의 여러 최적화 기법을 사용할 수 없기 때문에 세부적인 물리적 제어가 필요할 때만 RDD를 명시적으로 사용해야 한다.

3.2. 분산형 공유 변수

브로드캐스트 변수는 불변의 값을 closure 함수의 변수로 캡슐화하지 않고 클러스터에서 효율적으로 공유하게 해준다. 모든 워커 노드에 큰 값을 저장하여 재전송 없이 많은 Spark 액션에서 재사용이 가능하다. 모든 Task마다 직렬화할 필요 없이 클러스터의 모든 머신에 캐시하게 된다.

브로드캐스트 변수는 다방면에서 활용될 수 있는데, 이후에 설명할 broadcast join에서 그 효과를 직관적으로 이해할 수 있을 것이다.

어큐멀레이터는 Spark 클러스터에서 row단위로 안전하게 값을 갱신할 수 있는 변경 가능한 변수를 제공한다. 이를 디버깅용이나 저수준 집계용으로 사용할 수 있다. 예를 들어 파티션 별로 특정 변수의 값을 추적하는 용도로 사용할 수 있고 병렬 처리 과정에서 더욱 효율적으로 사용할 수 있음. 기본적으로 Spark는 수치형 어큐멀레이터를 지원하나 사용자 정의 형태도 가능하다.

어큐멀레이터에 이름을 지정하면 이 실행 결과는 Spark Web UI에 표시되기 때문에 모니터링하기에 매우 편리하다.

4. 애플리케이션, Job, Stage, Task 개념

이전에 Transformation과 Action의 개념에 대해서 설명하였다. Action이 실제로 어떤 연산을 하는 작업이라고 하였다. 이 Action 하나당 1개의 Job이 존재한다. 그리고 이 Job은 일련의 Stage와 Task들로 구성된다.

Stage는 다수의 머신에서 Task의 그룹이다. Task들은 모두 동일한 연산을 수행하게 되는데, 파티션 1개당 1개의 task가 주어진다. 그리고 Executor는 1개의 파티션에 대해 작업을 처리하게 된다. 그림으로 보면 아래와 같다.

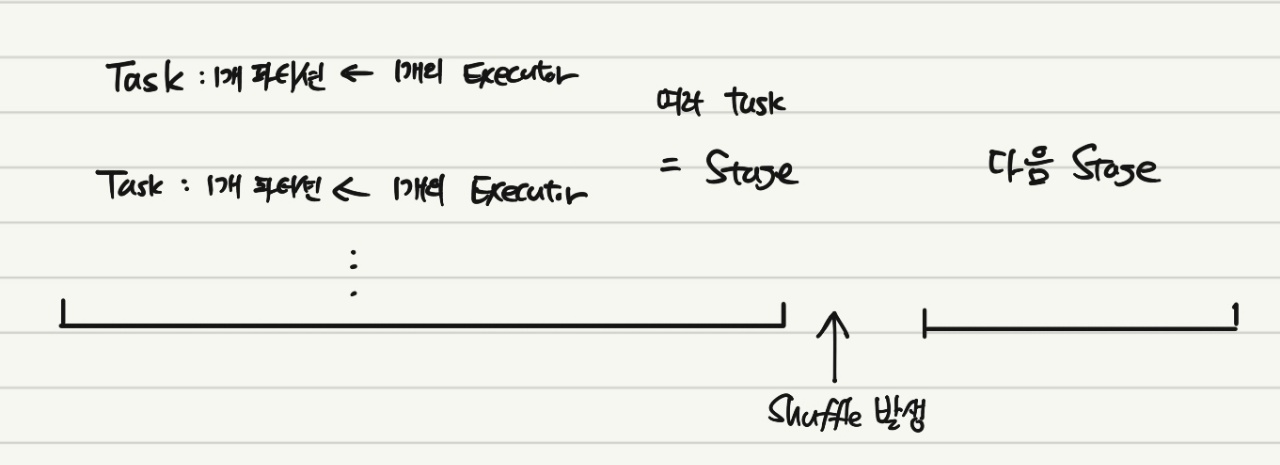
위 설명처럼, 각 Stage는 Shuffle이 발생했는지의 여부에 따라 구분되게 된다. 참고로 Shuffle은 각 노드 사이에 데이터의 이동이 발생하는 것을 의미한다.

그리고 최종적으로 이러한 여러 Job들이 모여 전체 Spark 애플리케이션을 구성한다.

5. Join

Spark에서의 Join을 찾아보면, Shuffle Join, Broadcast Join, Sort Merge Join이 나올 것이다. 그런데 Shuffle Join은 Spark2.3에서부터 Sort Merge Join으로 대체되었다. (설정으로 변경할 수 있다.) Sort Merge Join이 Shuffle Join에 비해 클러스터내 데이터 이동이 더 적다고 알려져 있다.

Sort Merge Join은 사용자가 일반적으로 DataFrame에 join을 행하면 가장 많이 일어나는 join이다. 먼저 파티션을 정렬한 후 이 정렬된 데이터를 병합하면서 join key가 같은 row를 join하게 된다. 먼저 정렬을 하기 때문에 데이터가 심하게 뒤섞여 있거나 skewed되어 있으면 이 비용이 상당히 크다.

Broadcast Join은 작은 테이블을 큰 테이블에 join할 때 사용된다. 작은 테이블을 클러스터 전체 worker node에 복제하고 이를 캐시하여 계속 사용하는 것인데, 한 번 대규모 통신이 발생하긴 하지만 (이 때의 비용은 클 것이다.) 이후 추가적인 통신이 없기 때문에 굉장히 유용하고 실제로 크게 속도를 향상시켜준다. 보통 이러한 상황에서 Spark는 알아서 Broadcast Join으로 계획을 수립한다. (구조적 API를 사용할 때)

Join 수행 시 시간이 너무 오래걸린다고 생각이 되면 아래 Tip들을 참고하면 좋다.

• Join될 파티션들이 최대한 같은 곳에 있어야 한다.
• DataFrame의 데이터가 균등하게 분배되어 있어야 한다. (not skewed)
• 병렬 처리가 이루어지려면 일정한 수의 고유 key가 있어야 한다.

위와 같은 과정에 대해서 좀 더 자세한 설명이 필요하다면 아래 링크를 참조하면 좋다.

• Handling Data Skew in Apache Spark
• The art of joining in Spark

6. Spark Execution 최적화

이전에 기술하였듯이 Shuffle이 발생하면 Stage는 새로 생성하고, 각 Stage는 파티션 개수에 따라 여러 Task로 쪼개진다. 이 Task의 수행 시간은 아래와 같이 또 쪼개볼 수 있다.

Scheduler Delay + Deserialization Time + Shuffle Read Time(Optional) + Executor Runtime + Shuffle Write(Optional) + Result Serialization Time + Getting Result Time

Spark Web UI를 켜셔 Job 모니터링을 하면 자주 볼 수 있는 용어들이다.

Scheduler Delay에 대해 알아보자. Spark는 Data Locality에 크게 영향을 받는다. 데이터가 실제 위치한, 로드된 곳이라고 생각하면 되는데 Spark는 이 데이터 전송을 최소화하기 위해 Task를 데이터와 최대한 가깝게 하여 수행하려고 한다. Data Locality는 아래와 같이 5개로 구분된다.

상위에 있을수록 좋은 것인데, 만약 Data Locality가 PROCESS_LOCAL이라면 Task는 굉장히 빠르게 진행될 것이다. 아래에 있는 레벨일 수록 실제로 Task를 수행할 때까지의 시간이 길어지고, 이를 Scheduler Delay라고 한다. 즉, 네트워크 전송 비용이 그만큼 사용된다는 것이다.

만약 가용 Executor가 Data Locality를 만족하지 못하면 timeout까지 그냥 기다리게 되기 때문에 spark.locality.wait 파라미터를 조정할 수 있다. 더 나은 Locality를 위해 더욱 긴 waiting time을 설정하거나 waiting time을 0으로 바꿔버림으로써 이전 단계들을 건너뛸 수도 있다.

이 Data Locality가 낮은 레벨에 속해있고, Shuffle 대상 데이터의 크기가 크다면 이후 Shuffle Read/Write Time은 크게 증가하게 될 것이다. Executor Run Time은 data read/write time, CPU execution time, Java GC time으로 구성된다.

Task의 수행 시간에 대해서는 알아보았고, 그렇다면 좀 더 빠르게 작업이 진행되도록 튜닝을 하려면 어떻게 해야할까? 이 부분은 Spark 완벽 가이드 책과, IBM 그리고 Databricks의 포스팅을 참고하여 요약 정리한다.

먼저 간접적인 성능 향상 기법에 대해 정리한다. 일단 구조화 API를 적극 사용해야 한다. 이전에도 언급하였듯이 구조적 API를 사용하면 Spark의 여러 장점들을 그대로 사용할 수 있다. RDD의 사용 영역은 최소화하는 것이 좋다. 특히 Python으로 RDD 코드를 실행하면 JVM과 Python 프로세스를 오가는 많은 데이터를 직렬화/역직렬화해야 해서 많은 비용이 수반된다.

그리고 다음은 Data Locality를 확인해보는 것이다. 지금 수행하고 있는 Task에 대한 Data Locality가 과연 최선인지 파악해보아야 한다. 다음으로는 Shuffle 설정이다. 이 부분이 상당히 중요하다. Shuffle은 일반적으로 큰 네트워크 비용을 요구하기 때문에 지양되곤 한다. 불필요한 Shuffle은 당연히 피하는 것이 좋다. 그러나 애초에 Shuffle이 존재하는 이유는 데이터를 재 분배하여 더욱 효율적인 처리를 가능하게 만들기 위해서이다. 즉, 잘만 사용하면 성능 향상을 이끌어낼 수 있다.

Data Skeweness가 발견되었거나 파티션 수가 너무 적으면 Shuffle이 도움이 된다. 일단 특정 파티션에만 데이터가 몰려있으면 그 파티션에서 task를 수행하는 Executor의 부담이 커지기 때문에 다른 Executor들의 작업이 끝나도 전체 Stage가 끝나지 않는 현상이 발생하게 된다. 또 애초에 파티션 수가 너무 적으면 작업을 수행하지 않는 Executor가 발생할 수도 있기 때문에 파티션 수 조정이 도움이 되는 경우가 많다. 예를 들어 기본 파티션의 수가 200개이기 때문에 task가 200개로 쪼개져 있을 때, 가용 node의 수가 130개라고 하면, 모든 node의 작업이 끝난 후에 오직 70개의 node만이 2번째 작업을 시작하게 될 것이다. 이는 분명 효율을 다소 낮추는 요인이 된다.

추가적으로 Shuffle을 수행할 때는 Output 파티션 당 최소 수십 메가바이트의 데이터는 포함되는 것이 좋으며, 애플리케이션이 실행 중에 메모리를 너무 많이 사용하거나 GC collection이 너무 자주 수행되는 것은 아닌지 확인해보는 것이 좋다.

직접적인 성능 향상 기법에 대해 알아보자. Executor 당 할당되는 CPU 코어의 수, 그리고 CPU 코어에 할당되는 task 수의 재조정을 통해 병렬화를 향상시킬 수 있다.

파티션 재분배(repartition)는 앞서 언급하였듯이 Shuffle을 수반하지만 데이터가 클러스터에 균등하게 분배되므로 Job의 전체 실행 단계를 최적화할 수 있다. 그리고 만약 Shuffle 없이 파티션의 수를 줄이고 싶다면 Coalesce 메서드를 통해 동일 노드의 파티션을 하나로 합칠 수 있다. 구조화 API 상태에서 repartition을 수행하면 생각보다 괜찮은 성능 향상을 보이는 경우가 많다.

현재의 파티션 기준을 변경할 수 있는데, 특정 칼럼을 기준으로 바로 설정할 수도 있고 사용자 정의 파티셔닝을 사용할 수도 있다. 사실 이 부분은 직접 반영해본 적은 없는데, 사용자 정의 파티션 함수를 생성한 뒤 이를 파티션의 기준으로 삼을 수 있다고 한다. 잘 제어하면 skewed된 데이터를 균등 분배할 수 있다.

이론적인 부분에 대해서는 정리를 마쳤고, 개인적으로 Spark Web UI에서 자주 모니터링 하는 항목들에 대해 간략히 설명하고 마치도록 하겠다.

Shuffle Read Size부터 유심히 보게 된다. Shuffle이 발생했을 때 얼마나 많은 데이터에 대해 네트워크 전송 비용이 들어가는지 가늠할 수 있기 때문이다. Shuffle Spill Memory/Disk는 전체 task가 끝난 후에 집계되며 언제나 Spill Memory > Spill Disk 관계이다. Peak Executiom Memory는 앞서 설명한 accumulator 변수인데, 이 값은 Task 내에서 생성된 모든 데이터 구조의 peak size의 총합과 거의 일치한다. 따라서 내가 다루고 있는 데이터의 전체 size에 대해 추정해볼 수 있다.

7. Apache Arrow

Apache Arrow는 Spark에서만 쓰이는 라이브러리는 아니지만, Spark에서 대단히 중요한 역할을 한다. in-memory columnar 데이터 포맷으로 JVM과 Python 프로세스 사이의 효율적인 데이터 전송 및 변환을 수행하는데, 메모리 공유를 통해 빠른 변환을 가능하게 한다. 또한 Tensorflow 및 Pytorch와도 고성능 데이터 교환 수단을 지원하기 때문에 만약 Spark 2.3.0 이상의 버전을 사용하고 있다면 거의 필수적으로 사용해야 하는 라이브러리이다. Arrow가 설치되어 있으면 효율적인 Vectorized UDF인 Pandas UDF를 사용할 수 있다. Pandas UDF를 사용하면 직렬화 overhead가 거의 발생하지 않기 때문에 속도를 굉장히 향상시킬 수 있다.

References

1) Spark 완벽 가이드 by 빌 체임버스, 마테이 자하리아
2) 참고 블로그
3) 참고 블로그
4) 참고 Medium글
5) 참고 Medium글
6) IBM Docs

이번 글에서는 SIGN이란 알고리즘에 대해 다뤄보겠다. 상세한 내용은 논문 원본을 참고하길 바라며, 본 글에서는 핵심적인 부분에 대해 요약 정리하도록 할 것이다. Twitter Research의 Gitub에서 코드를 참고할 수도 있다.

torch_geomectric을 이용하여 SIGN를 사용하는 방법에 대해서 간단하게 Github에 정리하도록 할 것이다.

Scalable Inception Graph Neural Networks 설명

1. Background

Facebook이나 Twitter의 network를 그래프로 표현한다고 해보자. 정말 거대한 그래프가 형성될 것이다. 대다수의 GNN 연구들은 작은 그래프 데이터셋에서 성능 측정이 이루어지는 경우가 많다. 복잡하고 많은 관계들을 고려해야 하다보니 자연스레 GNN의 최대 문제 중 하나는 바로 scalability라고 할 수 있다.

SIGN은 기존에 많이 시도되었던 node-level 및 graph-level sampling 방법을 취하지 않고도 scalability를 달성한 알고리즘이다. sampling 방법에 의존하지 않기 때문에 최적화에 있어 개입될 수 있는 bias를 줄일 수 있다는 장점을 지닌다. 여러 데이터셋에 대한 실험 결과를 제시하고 있는데, 사용된 데이터셋 중 하나는 ogbn-papers100M으로, 110m nodes와 1.5b edges를 갖고 있다.

2. Architecture

SIGN의 구조는 inception module에서 영감을 받아 만들어 졌다.

위 그림과 같이 SIGN은 여러 유형 및 크기의 graph convolutional filter를 조합하고 이 결과에서 GNN을 적용하여 downtream task에 활용하는 방식의 구조를 갖고 있다. 이 때 filter에서 수행되는 연산의 중요한 부분은 model parameter의 영향을 받지 않아 미리 계산이 가능하기 때문에 빠른 학습 및 추론이 가능하다.

논문에서도 언급하였듯이 SIGN은 go deep 이냐 go wide 이냐에 대한 물음에 대한 하나의 답을 제안한다고 볼 수 있다. 복잡한 graph 구조의 데이터에서 유의미한 정보를 추출하기 위해 deep network를 구성할 수도 있지만 SIGN과 같이 shallow network이지만 여러 접근(go wide) 방법을 통해 이를 달성할 수도 있는 것이다.

SIGN을 식으로 나타내면 아래와 같다.

[\mathbf{Z} = \sigma( [ \mathbf{I} \mathbf{X} \mathbf{\Theta}_0, \mathbf{A}_1 \mathbf{X} \mathbf{\Theta}_1, …, \mathbf{A}_r \mathbf{X} \mathbf{\Theta}_r ] )]

[\mathbf{Y} = \sigma(\mathbf{Z} \mathbf{\Omega})]

$A$ 는 $(n, n)$, $X$ 는 $(n, d)$, $\theta$ 는 $(d, d^{\prime})$ 의 shape을 가진다. 따라서 이를 쭉 이어 붙이면 $Z$ 는 $(n, d^{\prime}(r+1))$ 의 shape을 갖게 될 것이다.

그렇다면 $\mathbf{A}_r \mathbf{X}_r$ 연산은 무엇일까. 일단 이 곱 연산에는 앞서 기술하였듯이 model parameter가 없기 때문에 미리 계산이 가능하다. graph가 크다면 이 역시 상당히 큰 연산이 되겠지만 병렬 시스템을 잘 이용하면 충분히 미리 계산할 수 있다고 설명하고 있다. 사실 이 부분이 SIGN의 가장 핵심 부분이다. $\mathbf{X}$ 는 node feature matrix가 될 것이다. 이렇게 하나의 matrix로 표현하였기 때문에 구조에 변형을 가하지 않으면 basic SIGN은 homogenous graph에만 적용이 가능하다. $\mathbf{A}_r$ 은 총 3가지 방법으로 계산될 수 있다.

1) power of simple normalized adjacency matrix
2) PPR based adjacency matrix
3) triangle-based adjacency matrix

논문에서는 위 3가지 operator를 조합하는 방식으로 실험 결과를 보여주고 있다. 1) 로 생각해보면, 주어진 인접 행렬에 대하여 여러 번 행렬 곱을 수행하여 새로운 인접 행렬을 얻는 작업으로 이해할 수 있다. PPR에 대해서는 이 글에서 간략한 설명을 확인할 수 있다.

3. Experiments & Insights

실험 결과에 대해서는 논문 원본을 참고하길 바란다. 여러 데이터셋에 대하여 성능과 수행 시간을 측정하였고, Hyperparameter tuning 과정에서도 상세하게 기술되어 있기 때문에 여러 인사이트를 얻을 수 있다.

대표적인 비교 대상은 ClusterGCN과 GraphSAINT 인데 두 알고리즘 모두 Scalability를 달성하기 위해 고안된 알고리즘들로 볼 수 있다.

몇 가지 인사이트 및 알아두어야 할 부분을 정리하며 글을 마무리한다.

1) 기본적으로 SIGN은 굉장히 빠른 속도를 보여준다. 전처리에 있어 다소 추가적인 작업이 필요하긴 하지만 미리 계산이 가능하다는 이점 때문에 충분히 극복이 가능할 것으로 보인다.
2) 논문에서도 기술하였지만, $\Theta_i$, $\Omega$ 로 표기된 연산은 single-layer projection 연산으로 한정되는 것이 아니라 MLP로 대체될 수 있다. 이는 곧 이 부분에서 다른 형태의 GNN layer를 사용할 수 있음을 의미한다. 흥미로운 연구가 될 수 있을 듯 하다.
3) PPR-based adjacency matrix는 inductive setting에서는 형편 없는 결과를 보여주었다고 한다. 이러한 결과는 논문에서 언급된 한 참고문헌의 결과와도 일치하는 결과라고 한다.
4) $\mathbf{A}_r$ 연산을 학습 가능한 연산으로 로 대체할 수 있다. 이를 위해 graph attention 메커니즘을 생각해볼 수 있는데, node/edge feature의 특징을 활용하여 더욱 효과적인 결과물을 만들어 낼 수도 있을 것이다. 다만 그대로 적용할 경우 미리 계산할 수 있다는 SIGN의 장점을 잃어버리기 때문에 graph의 작은 subset으로 학습을 진행한 후 attention parameter를 고정하여 일괄적으로 적용하는 것을 추천하고 있다.

참고로 Pytorch Geometric에서는 torch_geometric.transforms.SIGN을 통해 SIGN 연산을 지원하고 있다. 다만 Source Code를 보면 확인할 수 있듯이 simple normalized adjacency matrix에 의한 연산만을 제공하고 있기에 다른 연산을 활용하고 싶다면 수정이 필요하다.

본 글에서는 총 3가지의 Graph Pooling에 대해 핵심 부분을 추려서 정리해 볼 것이다. gPool, DiffPool, EigenPool이 그 주인공들이며, 상세한 내용은 글 하단에 있는 논문 원본 링크를 참조하길 바란다.

Github에 관련 코드 또한 정리해서 업데이트할 예정이다.

gPool(Graph U-nets) 설명

graph pooling은 간단하게 말하자면 full graph에서 (목적에 맞게) 중요한 부분을 추출하여 좀 더 작은 그래프를 생성하는 것으로 생각할 수 있다. subgraph를 추출하는 것도 이와 맥락을 같이 하기는 하지만, 보통 subgraph 추출은 그때 그때 학습에 필요한 아주 작은 부분 집합을 추출하는 것에 가깝고, graph pooling은 전체 그래프의 크기와 밀도를 줄이는 과정으로 생각해볼 수 있다.

단순한 그림 예시는 아래와 같다.

locality 정보를 갖고 있는 grid 형식의 2D 이미지를 다룬 CNN과 달리 그래프 데이터에 바로 pooling과 up-sampling을 수행하는 것은 어려운 작업이다. 본 논문에서는 U-net의 구조를 차용하여 그래프 구조의 데이터에 pooling과 up-sampling(unpooling) 과정을 적용하는 방법에 대해 소개하고 있다.

pooling 과정은 gPool layer에서 수행되며, 학습 가능한 projection 벡터에 project된 scalar 값에 기반하여 일부 node를 선택하여 작은 그래프를 만드는 것이다. unpooling 과정은 gUnpool layer에서 수행되며, 기존 gPool layer에서 선택된 node의 position 정보를 바탕으로 원본 그래프를 복원하게 된다.

모든 node feature는 projection을 통해 1D 값으로 변환된다.

[y_i = \frac{\mathbf{x_i} \mathbf{p}}{\Vert \mathbf{p} \Vert}]

$\mathbf{x_i}$ 는 node feature 벡터이고, 이 벡터는 학습 가능한 projection 벡터 $\mathbf{p}$ 와의 계산을 통해 하나의 scalar 값으로 변환된다. 이 때 $y_i$ 는 projection 벡터 방향으로 투사되었을 때 node $i$ 의 정보를 얼마나 보존하고 있는지를 측정하게 된다. 연산 후에 이 값이 높은 $k$ 개의 node를 선택하면 k-max pooling 과정이 이루어지는 것이다.

참고로 논문에서 모든 계산은 full graph 기준으로 이루어진다. 계산 과정은 아래와 같다.

[\mathbf{y} = \frac{X^l \mathbf{p}^l}{\Vert \mathbf{p}^l \Vert}]

[idx = rank(\mathbf{y}, k)]

[\tilde{\mathbf{y}} = \sigma(\mathbf{y}(idx))]

[\tilde{X^l} = X^l(idx, :)]

[A^{l+1} = A^l (idx, idx)]

[X^{l+1} = \tilde{X}^l \odot (\tilde{\mathbf{y}} \mathbf{1}_C^T)]

$\tilde{X}^l$ 이 $(k, C)$ 의 형상을 가졌고, $\tilde{\mathbf{y}}$ 는 $(k, 1)$ 의 형상을, $\mathbf{1}$ 은 $(C, 1)$ 의 형상을 갖고 있다.

$(\tilde{\mathbf{y}} \mathbf{1}_C^T)$ 는 아래와 같이 생겼다.

[\begin{bmatrix} y_1 \dots y_1
\vdots \ddots \vdots
y_k \dots y_k \end{bmatrix}]

과정을 그림으로 보면 아래와 같다.

gUnpooling 과정은 아래와 같이 extracted feature 행렬과 선택된 node의 위치 정보를 바탕으로 graph를 복원하는 방식으로 이루어진다.

[X^{l+1} = distribute(0_{N, C}, X^l, idx)]

이렇게 pooling 과정을 진행하다 보면 node 사이의 연결성이 약화되어 중요한 정보 손실이 많이 일어날 수도 있다. 이를 완화하기 위해 논문에서는 Adjacency Matrix를 2번 곱하여 Augmentation 효과를 취한다. 또한 self-loop의 중요성을 강조하기 위해 Adjacency Matrix에 Identity Matrix를 2번 더해주는 스킬이 사용되었다. 2가지 방법 모두 세부 사항을 조금 달리하면서 여러 GNN 논문에서 자주 등장하는 기법이다.

지금까지 설명한 gPooling과 gUnpooling, 그리고 GCN을 결합하면 Graph U-Nets가 완성된다.

이 모델은 node 분류 및 그래프 분류에서 사용될 수도 있으며, task에 따라 graph에서 중요한 정보를 추출하는 등의 목적으로 사용될 수 있다.

DiffPool(Hierarchical Graph Representation Learning with Differentiable Pooling) 설명

DiffPool 알고리즘은 많은 GNN 모델들이 graph-level classification 문제 상황에서 graph의 계층적 표현 정보를 학습하지 못한다는 한계점을 극복하기 위해 고안되었다. 왜냐하면 대다수의 pooling 방법들은 node embedding을 단순한 합 연산이나 신경망을 통해 globally pool하여 여러 계층 정보의 손실을 야기하기 때문이다.

DiffPool은 미분 가능한 graph pooling 모듈을 의미한다. nodes를 여러 클러스터에 mapping한 후, coarsened input으로 만들어 GNN layer의 input으로 취하는 과정을 통해 DiffPool의 update는 이루어진다. 이 때 클러스터는 input graph에서 잘 정의된 커뮤니티 정도로 생각할 수 있겠다. 이를 그림으로 나타내면 아래와 같다.

위 그림에서 유추할 수 있듯이, 본 방법론은 여러 GNN과 DiffPool layer를 쌓는(stacking) 방식을 통해 구현된다.

DiffPool에서 가장 중요한 요소 중 하나는 Assignment Matrix이다.

[S^l \in \mathcal{R}^{n_l, n_{l+1}}]

이 행렬은 layer $l$ 에서의 학습된 cluster assignment matrix인데, 이 행렬의 행은 $n_l$ nodes/clusters 중 하나로, 이 행렬의 열은 $n_{l+1}$ clusters의 하나에 해당한다. 즉, 이 행렬을 통해 2개의 layer를 연결하는 셈이다.

node features(embeddings)와 adjacency matrix는 아래와 같이 업데이트된다. 이 과정을 통해 점점 graph의 표현은 거칠어지고 압축되는 효과를 가져올 것이다.

[X^{l+1} = S^{l^T} Z^l, A^{l+1} = S^{l^T} A^l S^l]

학습은 2개의 구분된 GNN에 의해 이루어진다. 먼저 embedding GNN은 아래와 같다.

[Z^l = GNN_{l, embed} (A^l, X^l)]

논문에서는 GNN으로 GraphSAGE를 사용하였다.

pooling GNN은 아래와 같다.

[S^l = softmax(GNN_{l, pool}(A^l, X^l))]

이 때 softmax는 row-wise 함수이다. 두 GNN은 같은 input을 받지만 구분된 파라미터를 통해 학습한다.

다시 정리하면, $A^l, X^l$ 이 존재할 때, 이를 통해 먼저 $S^l, Z^l$ 을 학습시킬 수 있다. 그러면 이를 바탕으로 $X^{l+1}, A^{l+1}$ 을 업데이트하는 것이다.

최종적으로 1개의 클러스터를 형성하여 graph embedding을 수행하고 downstream task를 수행하게 된다.

논문에서는 2가지 문제점을 밝히고 있다. 일단 연산량이 상당하다는 점이 있는데 이 부분은 추후 연구 주제로 남겨두었다. 두 번째는 수렴이 어렵다는 점이다. 이 부분은 실제 적용에 있어 난제가 될 가능성이 높아 보이는데 논문에서는 이에 대해서 Regularization 항을 추가하는 방안을 제시하고 있다.

[L_{LP} = \Vert A^l, S^l S^{l^t} \Vert_F, L_E = \frac{1}{n} \Sigma_{i=1}^n H(S_i)]

이 때 $H$ 는 entropy 함수를 의미한다. 첫 번째는 link prediction objective를 추가한 것에 해당하고, 두 번째는 cluster assignment 행렬의 entropy 항을 추가한 것에 해당한다.

cluster의 수는 node 수의 10% 또는 25% 정도를 사용하였다고 나와있지만, 이 부분의 경우 학습으로 정할 수 있다고 밝히고 있다. cluster의 수가 많으면 계층적 구조를 더욱 잘 모델링할 수 있지만 noise가 발생하고 효율이 떨어질 수 있다고 한다.

EigenPool(Graph Convolutional Networks with EigenPooling) 설명

to be updated…

References

1) gPool 논문 원본
2) DiffPool 논문 원본
3) EigenPool 논문 원본