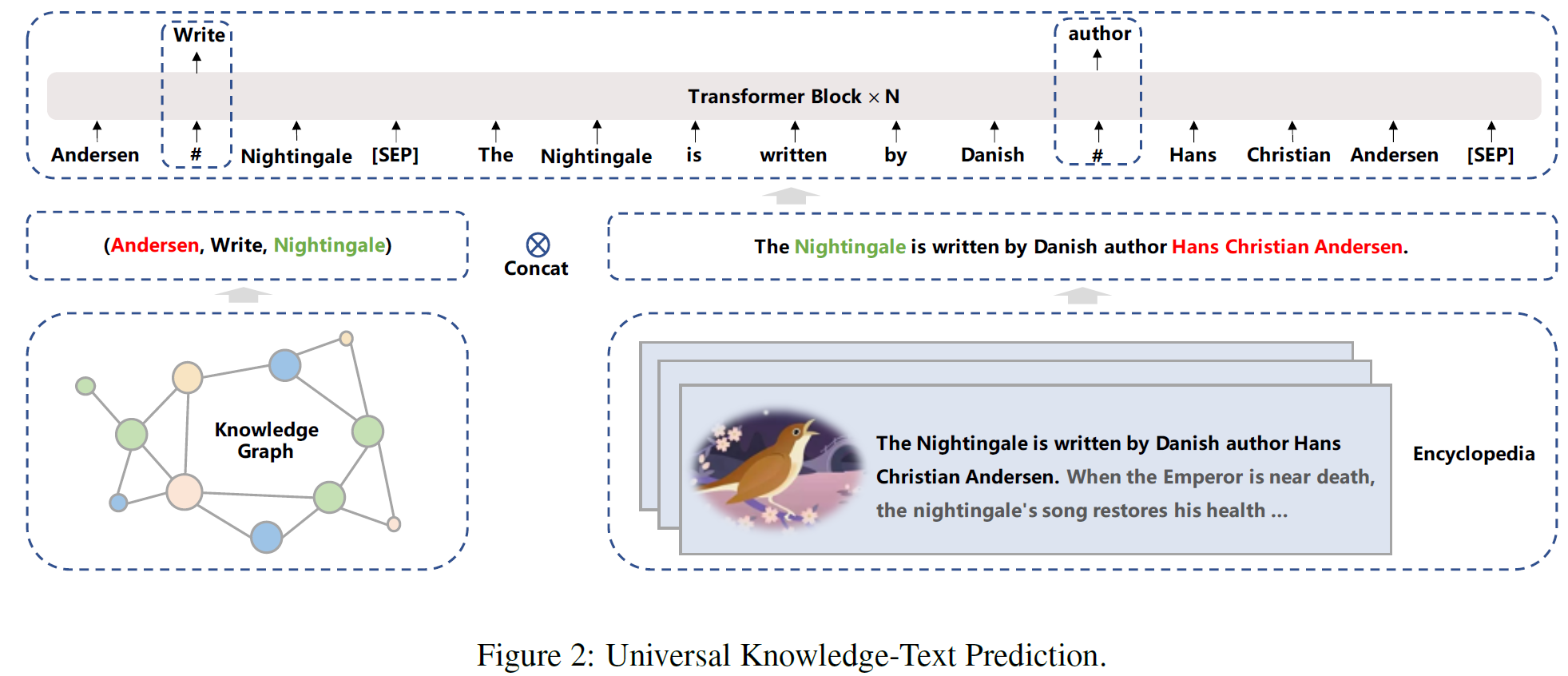
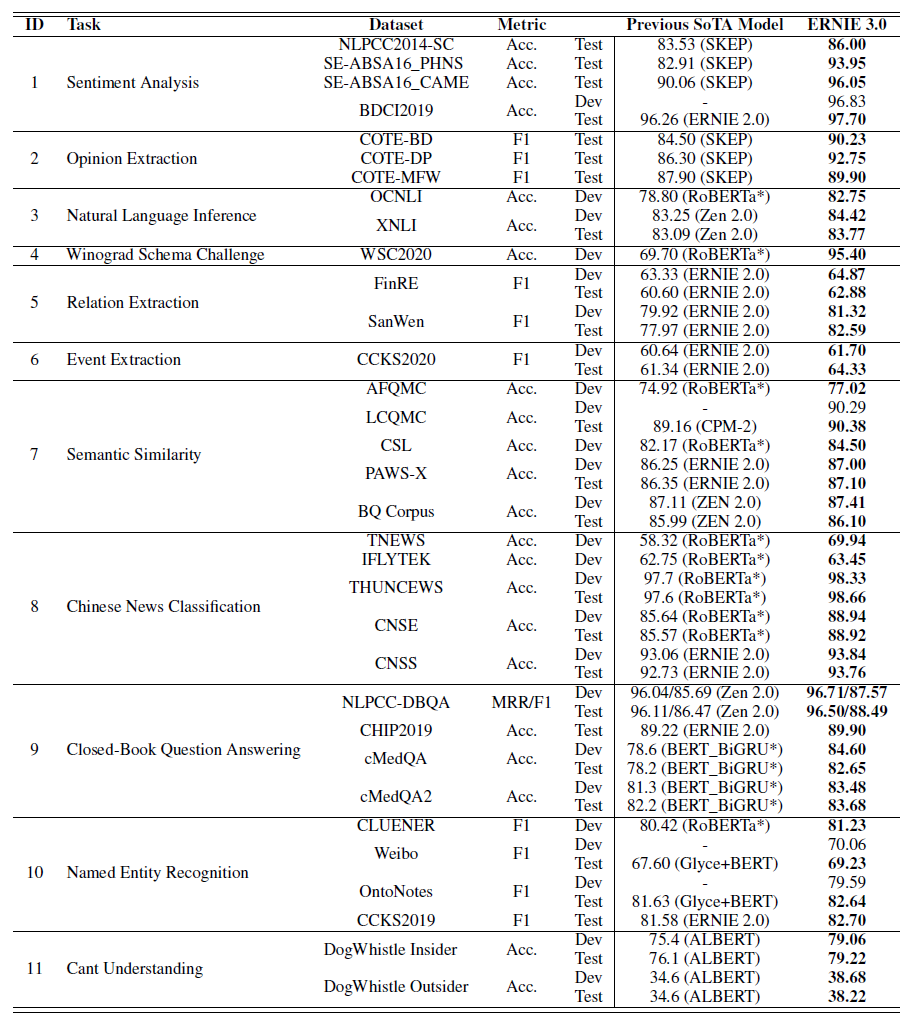
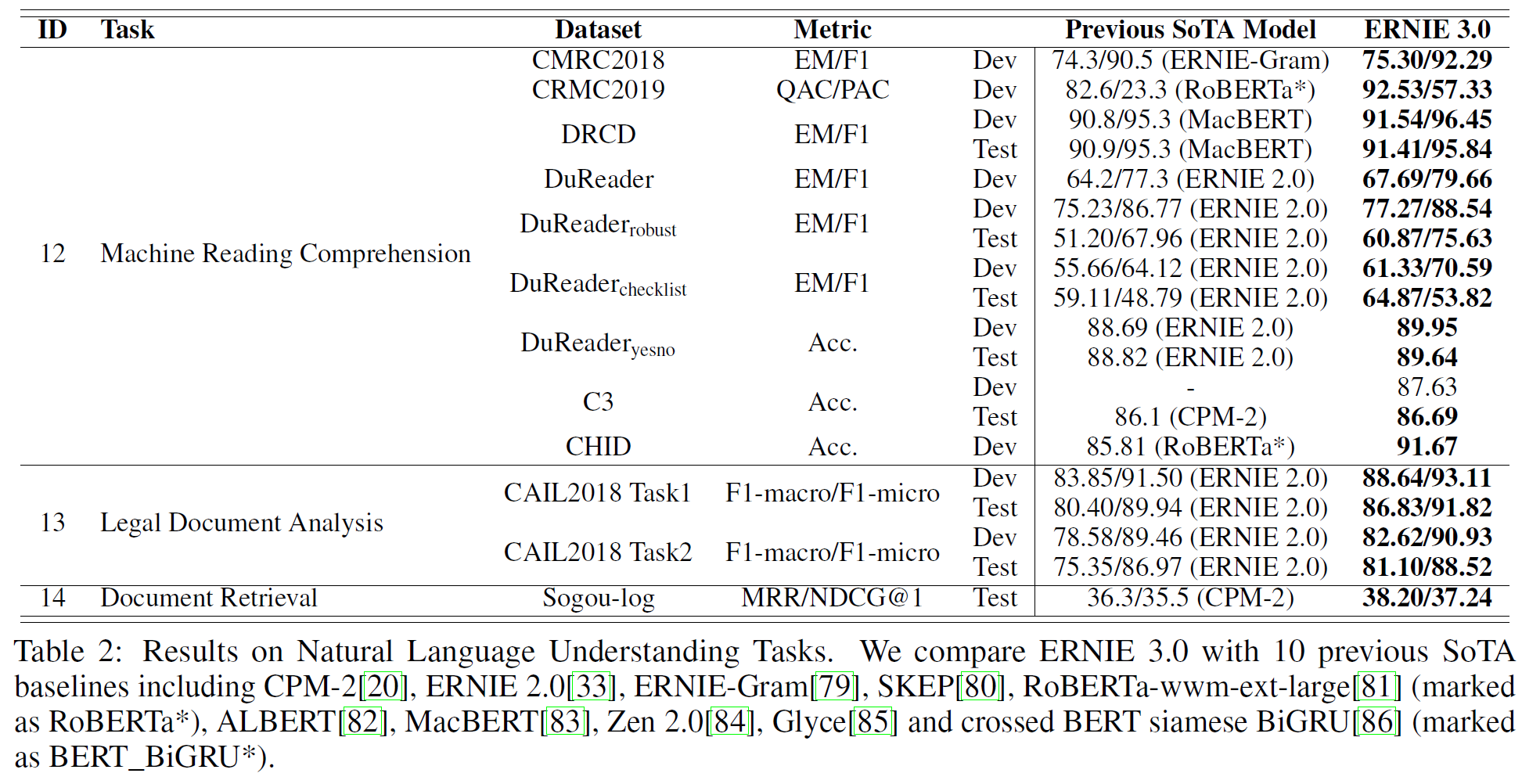
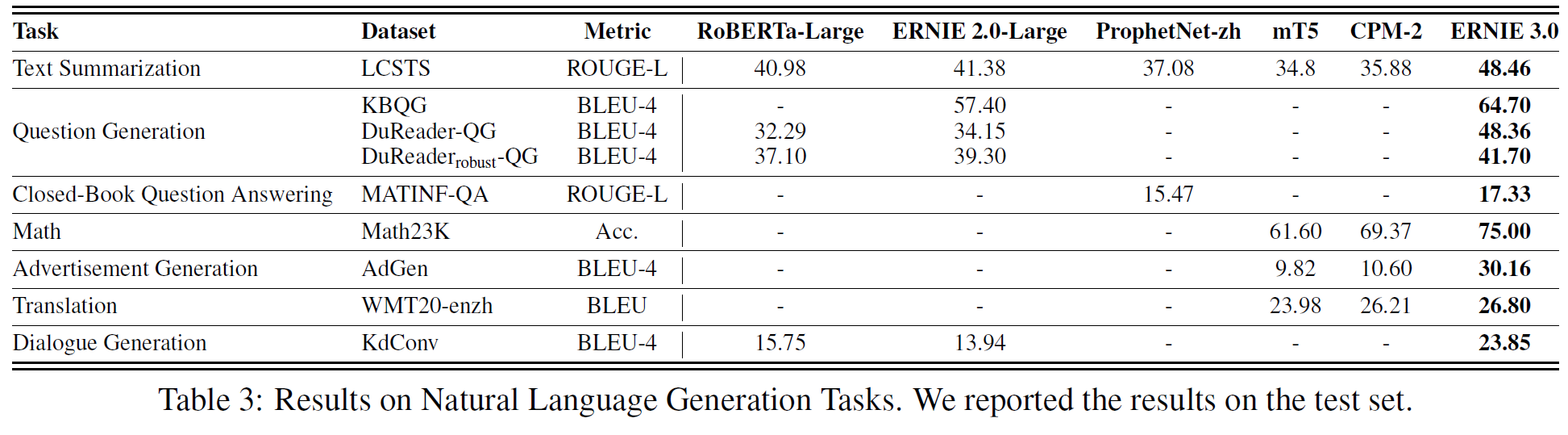
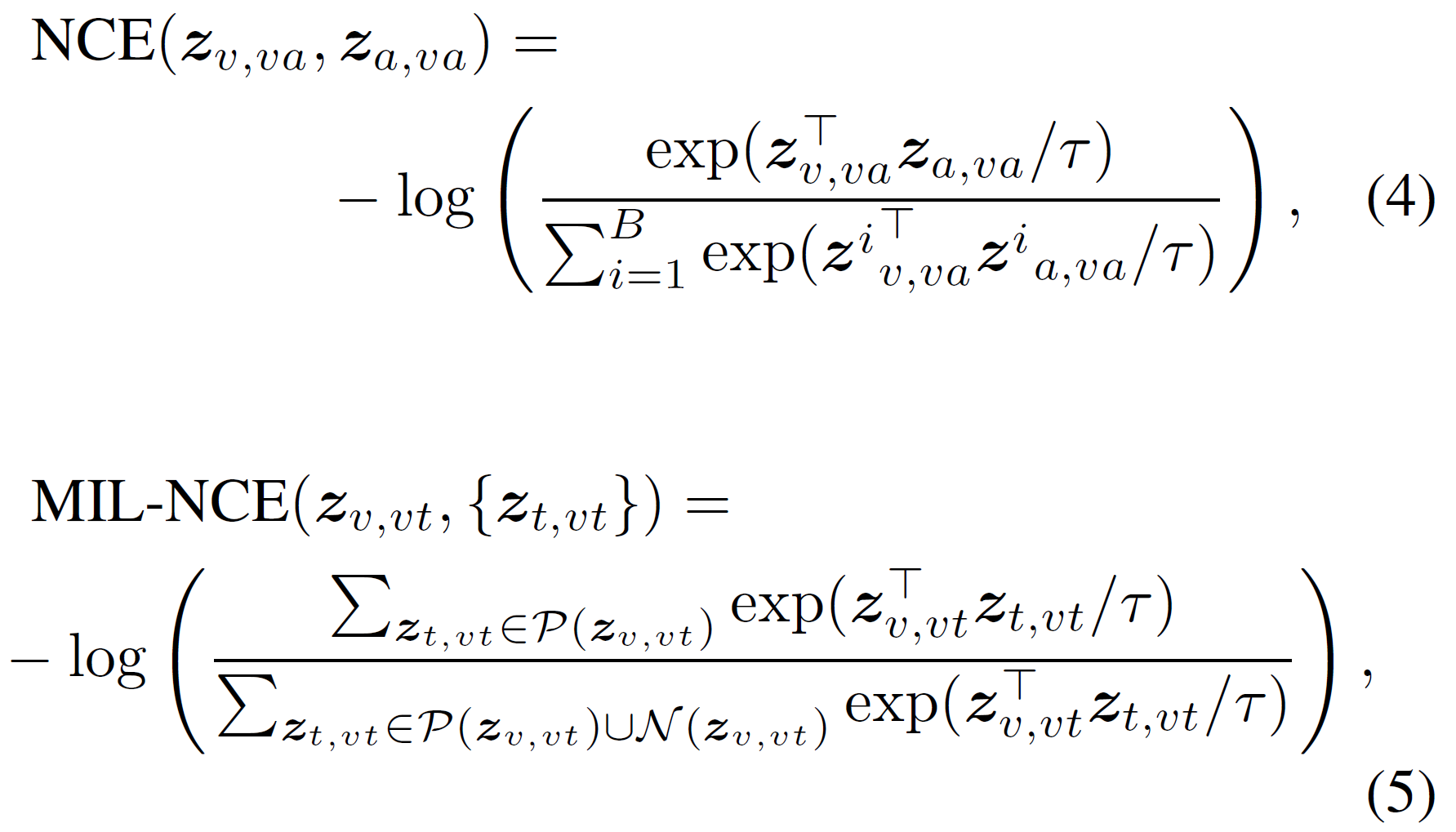이 글에서는 2021년 4월 arXiv에 올라온 VATT: Transformers for Multimodal Self-Supervised Learning from Raw Video, Audio and Text 논문을 살펴보고자 한다.
중요한 부분만 적을 예정이므로 전체가 궁금하면 원 논문을 찾아 읽어보면 된다.
VATT: Transformers for Multimodal Self-Supervised Learning from Raw Video, Audio and Text
논문 링크: VATT: Transformers for Multimodal Self-Supervised Learning from Raw Video, Audio and Text
초록(Abstract)
Convolution을 사용하지 않는 Transformer 구조로 레이블이 없는 데이터로부터 multimodal 표현을 학습하는 framework를 제안한다. Video-Audio Text Transformer(VATT)는 입력으로 raw signal을 받고 다양한 downstream task에 상당한 도움을 주는 multimodal 표현을 추출한다. End-to-end 방식으로 contrastive loss를 사용하여 scratch에서 학습하고 영상 행동인식, audio event 분류, 이미지분류, text-to-video retrieval 등의 task에서 그 성능을 평가하였다. 또한 modality-agnostic한, 3개의 modality 간 weight를 공유하는 하나의 backbone Transformer를 연구하였다. Convolution-free VATT가 downstream task에서 ConvNet 기반 구조를 능가함을 Kinetics-400/600, Moments in Time 등에서 보였다. VATT는 이미지 분류나 audio event 인식 문제에서도 큰 성능 개선을 이루었다.
1. 서론(Introduction)
CNN은 다양한 computer vision task에서 성공적인 결과를 가져왔다. Convolution 연산은 여러 변형에 대해서 불변성을 가지는 연산으로 시각 데이터에서 효과적임이 입증되었다. 그러나 자연어처리 분야에서는 RNN과 CNN과 같이 강한 inductive bias를 갖는 모델에서부터 자기지도(self-attention) 연산에 기반한 더 일반적인 구조로 그 paradigm이 바뀌어 왔다. 특별히 Transformers는 사실상 자연어처리를 위핸 (표준) 모델이 되었다. 몇 년간 convolution과 attention을 사용한 모델이 여럿 제안되었다.
그러나 대규모 지도학습 기반 Transformer는 2가지 주요한 문제가 있다.
- “big visual data”의 큰 부분을 배제한다(레이블이 없고 구조화되지 않은 데이터). 이로 인해 모델은 어느 한쪽으로 편향된다.
- 엄청난 수의 parameter, 여러 hyperparameter과 더불어 학습량, 계산량, 소요 시간이 매우 크다.
그래서 (지도학습 대신) 대규모의, 레이블이 없는 데이터(raw signal)을 입력으로 받으면 어떨까? 자연어는 Transformer에 맞는 그 자체의 지도 능력이 있다. 자연어는 순차적으로 단어, 구, 문장이 문맥 내에 놓여져 있고 의미와 구문을 부여한다. 시각적 데이터의 경우 대부분의 지도 기작은 주장하건다 multimodal video이다. 영상은 디지털 세계에서 충분히 많고, 시간 정보와 cross-modality를 가지며, 따라서 사람이 일일이 주석을 달 필요 없이 그 자체로 지도 능력을 갖는다.
본 연구에서, 자기지도 방식의 3개의 multimodal 사전학습 Transformer는 인터넷 영상의 raw RGB frame, audio waveform, 음성을 전사한 텍스트를 입력으로 받는다. 이를 Video, Audio, Text Transformers(VATT)라 한다.
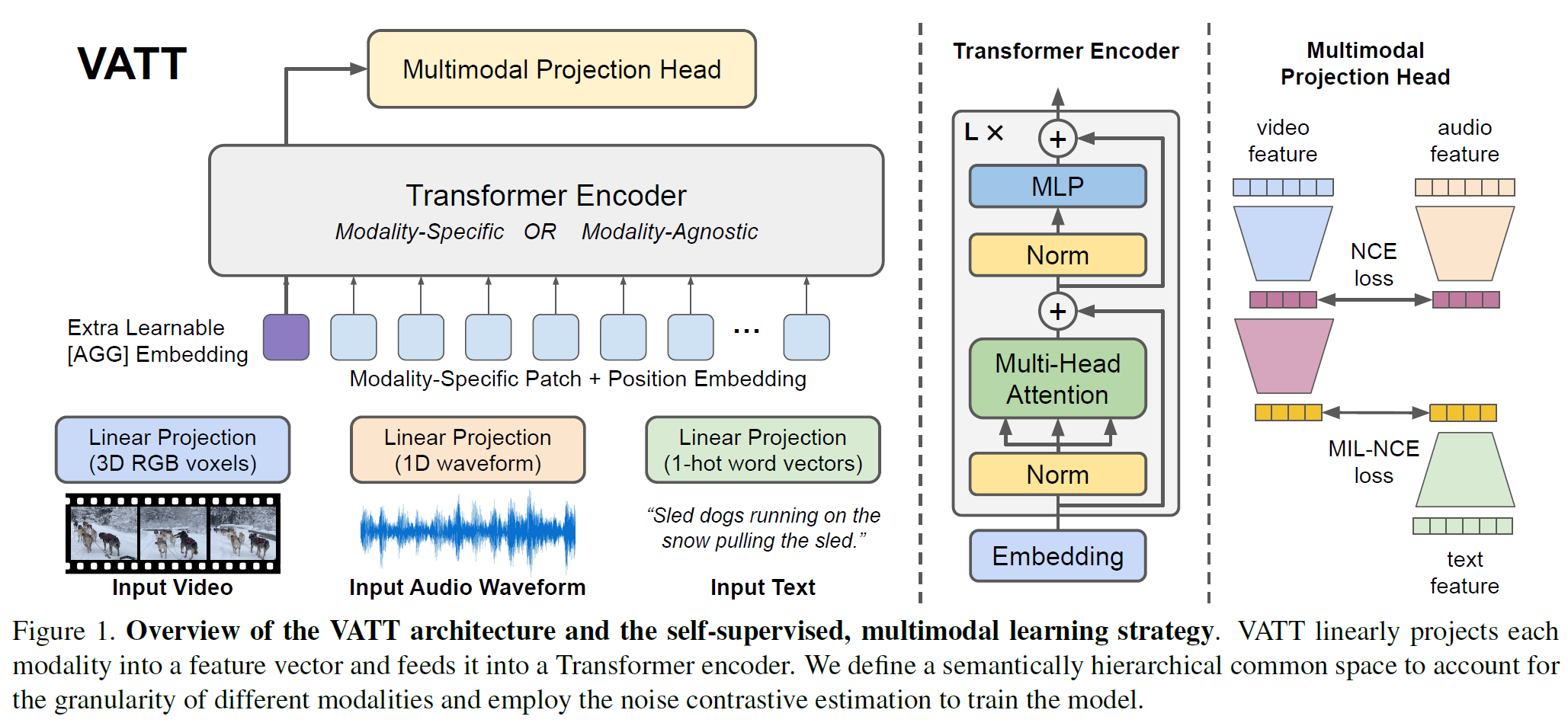
VATT는 BERT와 ViT과 같은 구조를 가지지만 각 modality별로 독립된 tokenization layer와 linear projection을 갖는 것만 다르다. 이는 최소한의 구조 변경만으로도 효과를 볼 수 있기 위함이며 자기지도 방식의 multimodal 학습 전략은 BERT와 GPT가 추구하는 사람이 만든 label은 최소한으로 쓰려는 목표와 동일한 방향성을 갖는다.
이 사전학습 Transformer는 자연어처리, 이미지 인식, 의미 분절, point cloud 분류, 행동인식 등에서 좋은 결과를 보였으며 Transformer가 여러 종류의 데이터에 대해서도 범용성을 가지는 구조임을 밝혔다.
여기에서 한발 더 나아가 VATT에 강한 제약을 걸었다(video, audio, text modality에 대해서 weight를 공유). Tokenization과 linear projection을 제외하고 모든 modality에 범용성을 갖는 하나의 구조가 존재할지를 테스트하는 것이다. Zero-shot video retrieval에서는 괜찮은 결과를 얻었으며 modality-agnostic한 Transformer는 modality에 특화된 모델과 비슷했다.
이 논문이 추가로 기여한 바는 DropToken으로, Transformer의 학습복잡도를 낮추는 간단하지만 효과적인 기법으로 video나 audio 중 임의로 일정 부분을 빼고 학습하는 방법으로, Transformer는 계산복잡도가 sequence의 제곱에 비례하기 때문에 상당히 효과적으로 계산량을 줄일 수 있는 방법이다.
원래 Transformer는 자연어처리 문제을 위해 고안된 모델 구조로 단어들의 장거리 연관성을 효과적으로 모델링하는 multi-head attention을 포함한다. 이러한 Transformer를 super-resolution, 물체탐지, multimodal 영상이해 문제 등의 vision task에 적용시키려는 시도가 많았으나 이들은 CNN으로 추출한 feature에 의존한다. 최근에는 convolution을 사용하지 않으면서도 그에 필적하는 성능을 가지는 모델이 제안되었다.
2.2 Self-Supervised Learning
Single vision modality: 자기지도 시각표현 학습 방법은 보통 auto-encoding, patch 위치 예측, 직소퍼즐, 이미지회전 예측과 같은 수동으로 지정된 pretext task를 통해 unlabeled 이미지로부터 학습한다. 이러한 최근의 contrastive 학습 방식의 트렌드는 데이터 증강과 instance discrimination을 통합한 방식으로 최근 많은 연구가 이루어지고 있다.
영상 부문에서는 시간적 signal을 pretext task로 사용하는 것이 자연스럽다. 미래의 frame 예측, 움직임/외형 통계, 속도/인코딩, frame이나 video clip 순서 정렬 등이 사용된다.
Multimodal video: Video는 본질적으로 multi-modal 데이터이다. Multiomdal 자기지도 학습은 영상이 오디오와 관련성이 있는지(일치하는지), cross-modality clustering, evolving losses 등을 예측하는 것으로 수행된다. 최근에는 contrastive loss를 사용하기도 한다.
VATT는 convolution-free Transformer와 multimodal contrastive learning을 결합한 (아마도) 최초의 연구이다.
3. 접근법(Approach)
여기서는 convolution-free 구조를 갖는 VATT를 설명하고 자기지도 multimodal 목적함수를 상술한다.

각 modality를 tokenization layer에 입력으로 주고 raw input은 embedding되어 Transformer에 들어간다. 여기에는 2가지 주요 세팅이 있다:
- Backbone Transformer가 분리되어 있으며 각 modality별로 고유의 weight를 갖는다.
- Transformer는 모든 modality에서 weight를 공유하는 단 하나만이 존재한다.
각 세팅에서, backbone은 modality-specific 표현을 추출하며 contrastive loss를 사용, 서로 비교하여 공유 공간(common space)르 매핑된다.
3.1. Tokenization and Positional Encoding
Vision modality는 frame별로 3채널 RGB 픽셀로 구성되어 있고, Audio는 waveform 형태로 되어 있으며 text는 일련의 단어로 구성된다. 먼저 modality-specifiv 토큰화 레이어를 정의하는데 이는 raw signal을 입력으로 받고 Transformer에 들어갈 일련의 vector를 출력한다. 또, 각 modality는 고유한 positional encoding을 가지며 Transformer에 들어갈 때 순서 정보를 알려준다.
Video
전체 clip이 $T \times H \times W$의 크기를 가지면, $\lceil T/t \rceil \cdot \lceil H/h \rceil \cdot \lceil W/w \rceil$의 patch로 구성, 각 patch는 $t \times h \times w \times 3$의 voxel을 가진다. 그리고 각 patch의 전체 voxel을 d차원 벡터표현으로 선형전사시킨다. 이 전사는 학습가능한 weight $W_{vp} \in \mathbb{R}^{t \times h \times w \times 3 \times d} $에 의해 이루어진다. 이는 An image is worth 16x16 words: Transformers for image recognition at scale에서 제안된 patching 방법의 3D 확장으로 볼 수 있다.
각 patch의 위치를 인코딩하기 위해 간단한 방법을 사용했다. 학습가능한 embedding의 dimension-specific sequence를 정의하여, 각 encoding 위치 $(i, j, k)$는 다음과 같다.
[\pmb{E}{\text{Temporal}} \in \mathbb{R}^{\lceil T/t \rceil \times d}
\pmb{E}{\text{Horizontal}} \in \mathbb{R}^{\lceil H/h \rceil \times d}
\quad \pmb{E}{\text{Vertical}} \in \mathbb{R}^{\lceil W/w \rceil \times d}
\pmb{e}{(i, j, k)} = \pmb{e}{\text{Temporal}_i} + \pmb{e}{\text{Horizontal}j} + \pmb{e}{\text{Vertical}_k}]
$\pmb{e}_i$는 $\pmb{E}$의 $i$번째 행이다. 이러한 방식은 positional embedding이 모든 patch를 인코딩할 수 있게 한다.
Audio
Raw audio waveform은 길이 $T^{‘}$의 1차원 입력으로 이를 각 $t^{‘}$ waveform amplitude를 포함하는 $\lceil T^{‘}/ t^{‘} \rceil $개의 부분으로 분절한다. Video와 비슷하게, 학습가능한 weight $W_{ap} \in \mathbb{R}^{t^{‘} \times d} $에 의해 선형전사가 이루어져 $d$차원의 벡터표현을 얻는다. $\lceil T^{‘}/ t^{‘} \rceil $개의 학습가능한 embedding으로 각 waveform 부분의 위치를 인코딩한다.
Text
학습 데이터셋에 존재하는 크기 $v$의 모든 단어의 사전을 만든다. 입력 text sequence의 각 단어는 학습가능한 weight $W_{tp} \in \mathbb{R}^{v \times d} $에 의해 $v$차원의 one-hot 벡터로 선형전사된다. 이는 embedding dictionary lookup과 동일한 과정이다.
3.1.1 DropToken
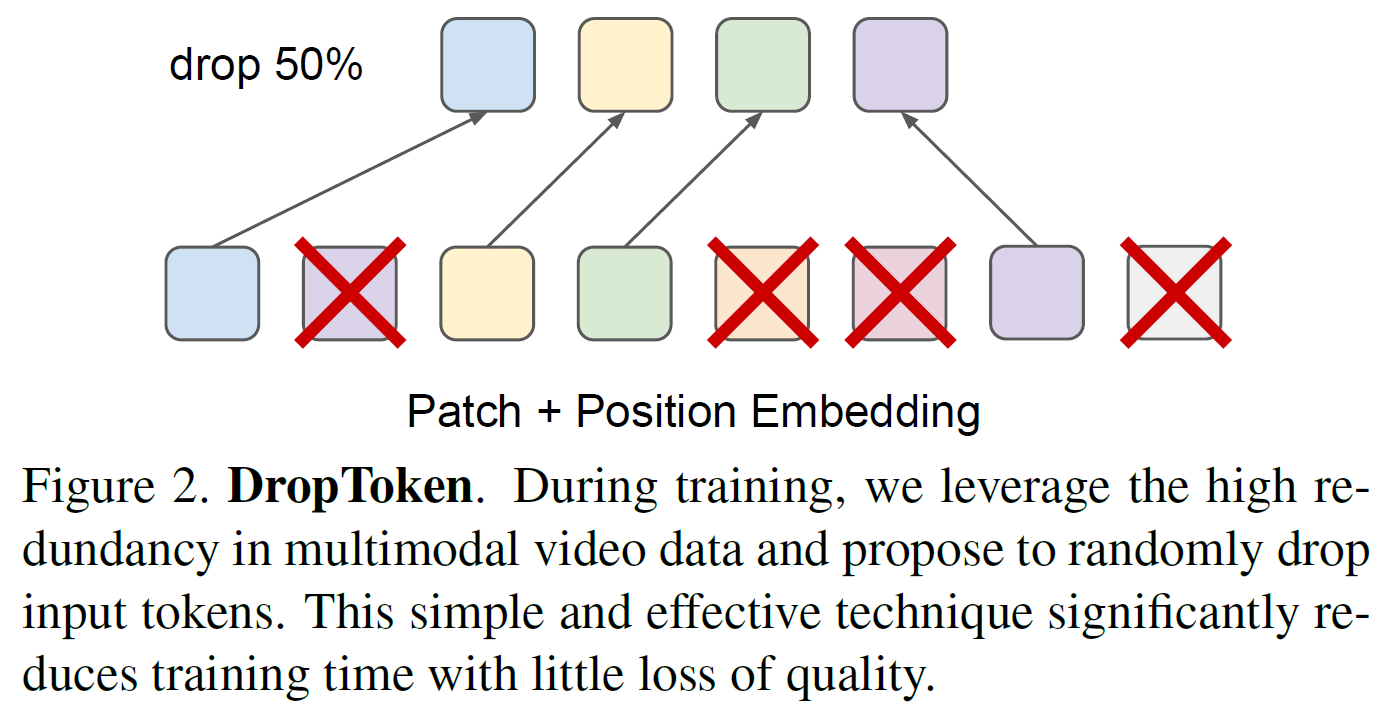
Transformer의 계산량을 효과적으로 줄이는 방법으로, Video나 Audio modality에서 일련의 입력이 들어오면, 일정 비율로 임의의 부분을 제거하고 모델에 입력으로 준다. 이는 Transformer의 계산복잡도는 입력의 길이 $N$에 대해 제곱에 비례, 즉 $O(N^2)$이기 때문에 상당히 효과적인 방법이다.
본 논문에서, 원본 입력의 해상도나 차원을 줄이는 대신, (고해상도 등) 정확도를 유지하면서 대신 DropToken을 사용하였다. Video나 Audio는 (인접한 부분에서) 중복성을 가지기 때문에 효율적인 방법이다.
ViT와 비슷한 Transformer 구조를 사용하고, 구조에 거의 변형을 가하지 않음으로써 이전의 weight로부터 쉽게 전이학습이 가능하게 하였다. 그림 1의 중간 부분에서 볼 수 있고, 구조를 수식으로 나타내면 다음과 같다.
[z_0 = [x_{\text{AGG}}; x_0\pmb{W}p; x_1\pmb{W}_p; … \ ; x_N\pmb{W}_p ] + e{\text{POS}}
z_l^{‘} = \text{MHA(LN}(z_{l-1})) + z_{l-1}, \quad l = 1…L
z_l = \text{MLP(LN}(z_l^{‘})) + z_l^{‘}, \quad \qquad l = 1…L
z_{\text{out}} = \text{LN}(z_L)]
$x_{\text{AGG}}$는 특수 aggregation token의 학습가능한 embedding으로 상응하는 Transformer의 출력 $z_{\text{out}}^0$은 전체 입력 sequence의 aggregated 표현으로 사용된다. 이는 추후에 분류 및 공통공간 매핑으로 사용된다. MHA는 Multi-Head Attention, NLP는 Multi-Layer Perceptron을 뜻하며 GeLU를 활성함수로 사용한다. LN은 Layer Normalization이다.
본 논문의 텍스트 모델은 position encoding $e_{\text{POS}}$를 제거하고 MHA 모듈의 첫 번째 layer의 각 attention score에 학습가능한 relative bias를 추가하였다. 이 간단한 수정을 통해 텍스트 모델이 SOTA 모델 T5로부터 바로 전이학습이 가능하게 만든다.
3.3. Common Space Projection
모델의 학습을 위해 공통공간으로의 전사(projection) 그리고 그 공통공간에서의 contrastive learning을 사용한다. 구체적으로, (video, audio, text) triplet이 주어지면, (video, audio) 쌍을 (video, text) 쌍과 같이 cosine 유사도로 직접 비교할 수 있도록 의미적으로 구조적인 공통공간 mapping을 정의한다. 이러한 비교는 여러 공간에서 여러 수준의 semantic granularity을 가정할 때 더 현실적이다. 이를 위해, 다수준 전사를 정의한다.
[z_{v, va} = g_{v \rightarrow va}(z_{\text{out}}^{\text{video}})
z_{a, va} = g_{a \rightarrow va}(z_{\text{out}}^{\text{audio}})
z_{t, vt} = g_{t \rightarrow vt}(z_{\text{out}}^{\text{text}}) \ \
z_{v, vt} = g_{v \rightarrow vt}(z_{v, va})]
$ g_{v \rightarrow va}, g_{a \rightarrow va}$는 video와 audio Transformer의 출력을 video-audio 공통공간 $\mathcal{S}{va}$로 전사한다.
$ g{t \rightarrow vt}, g_{v \rightarrow vt}$는 text Transformer의 출력과 $\mathcal{S}{va}$ 내의 video embedding를 video-text 공통 공간 $\mathcal{S}{vt}$로 전사한다.
이 다수준 공통공간 전사는 그림 1의 오른쪽 부분에서 볼 수 있다.
이 구조에서 볼 수 있는 주요한 점은 다른 modality는 다른 수준의 semantic granularity를 가진다는 것이며, 이를 위해 공통공간 전사에서 inductive bias를 도입하였다. $ g_{v \rightarrow va}$에서는 ReLU를 포함한 2-layer 전사가, 나머지는 선형전사가 포함되어 있다. 학습을 쉽게 하기 위해, 각 선형 layer 뒤에는 batch normalization이 붙어 있다.
3.4. Multimodal Contrastive Learning
레이블 없는 multimodal video는 충분히 구할 수 있으므로, VATT를 학습시키기 위해 자기지도 목적함수를 사용한다. video-text와 video-audio 쌍에 대해 Noise-Contrastive-Estimation(VCE)를 사용한다. (video, audio, text) stream이 주어진다고 가정하면, video-text와 audio-audio 쌍을 다른 시간대로부터 가져온다. Positive pair는 두 modality가 같은 video clip에서 선택된 것이며, Negative pair는 video, audio, text가 임의의 시간대에서 선택된 경우를 가리킨다. NCE 목적함수는 positive pair간 유사도를 최대화하고 negative pair간 유사도를 최소화하는 것이다.
본 논문에서 사전학습 데이터셋은 규격화된 ASR(Automatic Speech Recognition)로 얻은 텍스트를 사용하며 이는 꽤 noisy할 수 있다. 게다가, 일부 video는 음성이나 자막이 없는 경우도 있다. 따라서, Self-Supervised MultiModal Versatile Networks에서 제안된 NCE의 확장 버전 Multiple-Instance-Learning-NCE(MIL_NCE)를 사용, 영상 입력과 시간적으로 인접한 여러 텍스트 입력을 match시킨다. 이 변형 버전은 video-text 매칭에서 vanilla NCE보다 더 좋다.
본 논문에서는 video-audio 쌍에 대해서는 vanilla NCE를, video-text 쌍에 대해서는 MIL-NCE를 사용한다. 구체적으로, 섹션 3에서 설명한 공통공간에서 목적함수는 다음과 같다.
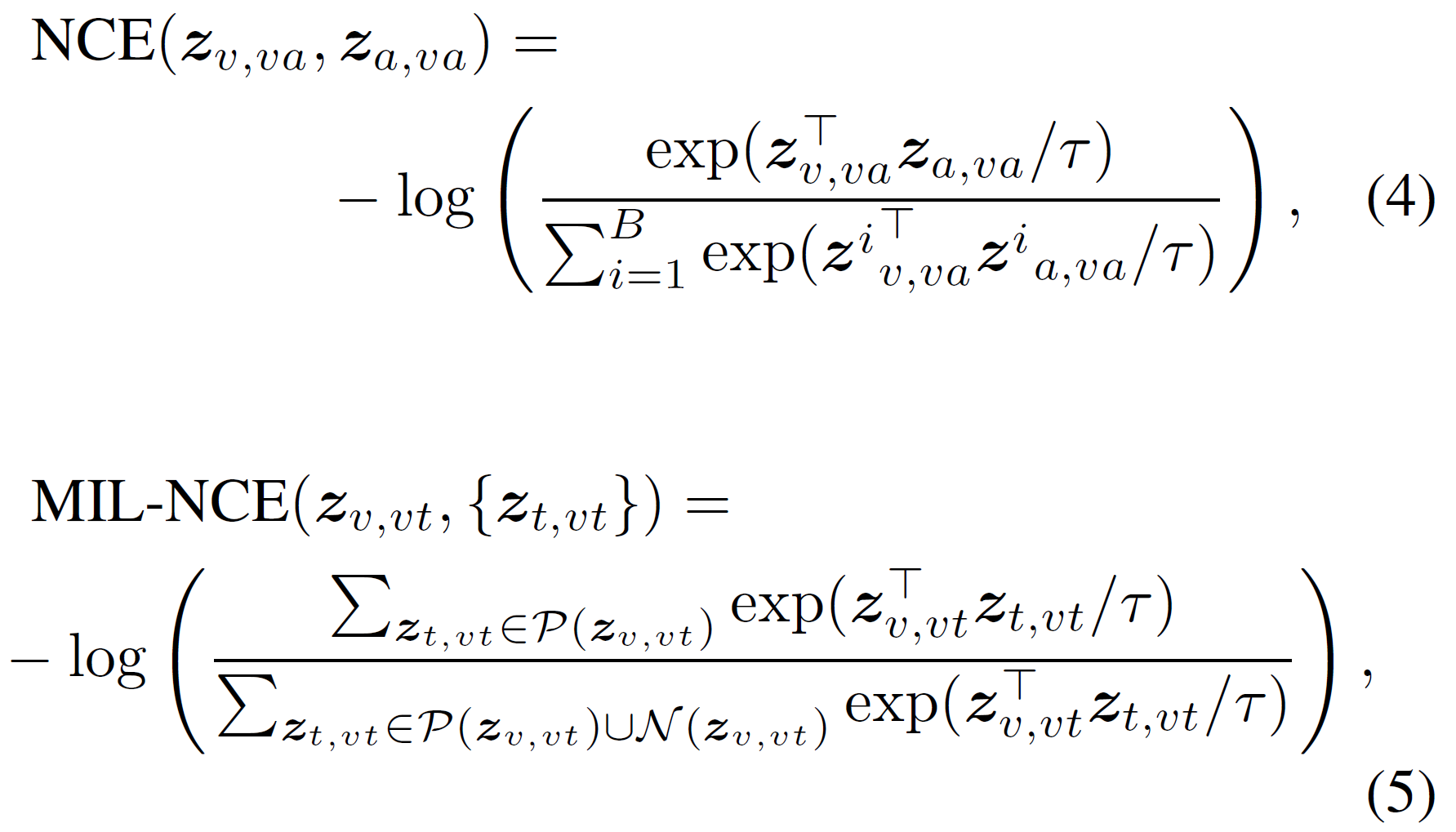
$B$는 batch size를 가리킨다. 각 반복에서 $B$개의 video-audio 쌍을 하나의 positive pair와 구성한다. $\mathcal{P}(z)$와 $\mathcal{N}(z)$는 각각 video clip $z_{v, vt}$ (시간적) 인근의 positive/negative text clip을 나타낸다. 구체적으로 $\mathcal{P}(z_{v, vt})$는 video clip과 시간적으로 가장 가까운 5개의 text clip을 포함한다. $\tau$는 negative pair로부터 positive pair를 구분하기 위한 목적함수의 부드러운 정도를 조절하는 온도 변수이다.
VATT의 전체 목적함수는 다음과 같다.
[\mathcal{L} = \text{NCE}(z_{v, va}, z_{a, va}) + \lambda \text{MIL-NCE}(z_{v, vt}, { z_{t, vt} })]
$\lambda$는 2개의 loss의 비율을 조절한다.
4. 실험(Experiments)
실험 환경과 결과, ablation study를 기술한다.
4.1. Pre-Training Datasets
VATT 사전학습 데이터로는 internet video(1.2M개의 영상, 136M개의 video-audio-text triplet 포함, 텍스트는 ASR로 얻음)와 AudioSet(유튜브 10초 clip에서 얻음)을 사용한다. 데이터셋의 어떤 레이블도 사용하지 않았고, AudioSet의 텍스트가 없는 부분을 채우기 위해서 text Transformer에 넣을 때는 $0$으로 채웠고 MIL-NCE loss에서 이러한 샘플은 제외했다.
4.2. Downstream Tasks and Datasets
여러 downstream task에서 VATT를 평가한다.
Video action recognition: 시각표현을 UCF101, HMDB51, Kinetics-400, Kinetics-600, Moments in Time에서 평가한다. UCF101과 HMDB51은 모델에 비해 크기가 작은 데이터셋이라 vision backbone은 고정하고 출력을 선형분류기를 학습하는 데 사용하였다. Kinetics-400, Kinetics-600, Moments in Time에 대해서는 사전학습 checkpoint로 초기화한 vision backbone을 미세조정하는 데 사용했다.
Audio event classification: ESC50, AudioSet으로 audio event 분류를 평가하였다. 위의 task와 비슷하게, ESC50은 audio Transformer을 고정시키고 선형분류기를 학습하는 데 사용하였다.
Zero-shot video retrieval: YouCook2와 MSR-VTT 데이터셋을 사용, video-text 공통공간 표현의 품질을 평가한다. Self-Supervised MultiModal Versatile Networks에서와 같은 평가방법과 Recall at 10(R@10)을 사용한다.
Image classification: 이미지와 영상 간 domain의 차이가 존재하지만, vision Transformer를 이미지 영역에서도 평가한다. ImageNet에서 vision Transformer의 마지막 checkpoint을 어떤 모델구조의 변형 없이 미세조정하여 평가하였다.
4.3. Experimental Setup
- 입력은 사전학습 데이터셋에서 32 frames, 10 fps를 사용하고 영역은 상대 비율로 [0.08, 1], 영상비율은 [0.5, 2]를 사용한다.
- 이후 $224 \times 224 $ 크기로 자르고 수평반전, color augmentation을 수행한다.
- 색깔, 밝기, 색조 등을 임의로 적용한다.
- 수치적 안정성을 위해 video와 audio 입력은 [-1, 1]로 정규화된다.
- video와 raw waveform 토큰화를 위해 patch 크기는 $4 \times 16 \times 16$과 $128$을 사용한다.
- 단어에 대해서는 $2^{16}$의 크기를 가지는 one-hot vector를 쓴다.
- text sequence는 자르거나 padding을 수행하여 길이 16으로 고정한다.
- 32 frames-2 stride, 25 fps, crop size=(320,320)이며 어느 token도 제외하지 않는다.
- audio와 text에 대해 입력 크기는 평가하는 동안 바꾸지 않는다.
Network Setup in VATT: 크기가 각각 다른 4개의 모델이 있다. modality-specific Transformer을 실험할 때 Small과 Base 모델을 text와 audio modality에 사용하고, video modality는 모델 크기를 변화시킨다. 그래서 modality-specific video-autio-text backbone (조합)은 3가지가 존재한다: Base-Base-Small(BBS), Medium-Base-Small(MBS), Large-Base-Small(LBS).
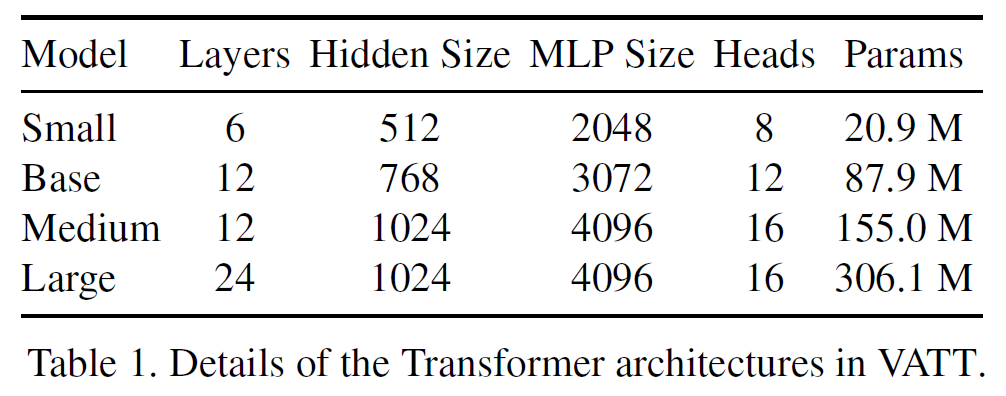
Projection heads and contrastive losses: 공통공간 $\mathcal{S}{va}, \mathcal{S}{vt}$로의 전사를 위해 $d_{va}=512, d_{vt}=256$를 사용했다. $\tau=0.07, \lambda=1$로 이는 Self-Supervised MultiModal Versatile Networks의 것과 같다. 이를 조정하면 더 좋은 결과를 얻을 수도 있다.
Pre-training setup: 초기 $lr=1e-4$, 10k warmup, 전체 500k step이며, batch size는 2048, lr은 quarter-period cosine schedule로 $1e-4 \rightarrow 5e-5$로 조정한다. 탐색 실험에서는 batch size는 512이다.
Tensorflow v2.4, 256 TPU로 3일간 학습했다.
Video fine-tuning setup: video action recognition을 위해 SGD(momentum=0.9), lr=0.005, 2.5k warmup step, batch size 64, 전체 100k step, half-period cosine schedule$\rightarrow 0$)을 사용한다. 비디오 프레임 해상도는 (320, 320)이다.
Audio fine-tuning setup: SGD를 사용하였으며, minibatch 안에서 입력 레이블 $x$-$y$ 쌍에 대해 mixup을 수행한다:
[x = \alpha x_1 + (1-\alpha)x_2, y = \alpha y_1 + (1-\alpha)y_2]
입력 레이블 쌍은 임의로 선택되었으며 mixing rate $\alpha$는 Beta(5, 5) 분포에서 선택된다.
Image fine-tuning setup: ImageNet으로 이미지 크기는 (384, 384), 512 batch size, SGD(0.9), lr(8e-2)이며 weight decay는 사용하지 않았다.
Linear evaluation setup: 모든 데이터셋과 task에서 고정된 backbone에 선형분류기를 사용했다. factorized weight $\pmb{C} = \pmb{UV} \in \mathbb{R}^{d \times c}$이며 $\pmb{U} \in \mathbb{R}^{d \times n}, \pmb{V} \in \mathbb{R}^{n \times c}$는 학습가능하다.
이 분류기를 학습시키는 동안 $\pmb{U}, \pmb{V}$의 $n$개의 component의 부분을 임의로 선택, low-rank 분류기 weight $\pmb{C}$로 유도한다. 분류기 weight $\pmb{C}$는 Adam optimizer(5e-4)를 사용하여 학습시킨다.
Zero-shot retrieval setup: MSR-VTT의 1k split, YouCook2의 전체 split을 사용했다. $224 \times 224$ 크기로 중간만 자른다(32 fps, stride 2, 25 fps). 각 입력 clip이 2.56초이고 전체 clip 길이는 10초이기 때문에 text query의 임베딩과 유사도를 계산하기 전에 4개의 동등하게 선택된 clip의 임베딩을 평균한다.
4.4. Results
4.4.1 Fine-tuning for video action recognition
아래 표는 Kinetics-400, 600에 대한 각 모델별 top-1, top-5(, TFLOPs) 결과를 비교한다. 표 4는 Moments in Time에 대한 실험 결과이다.
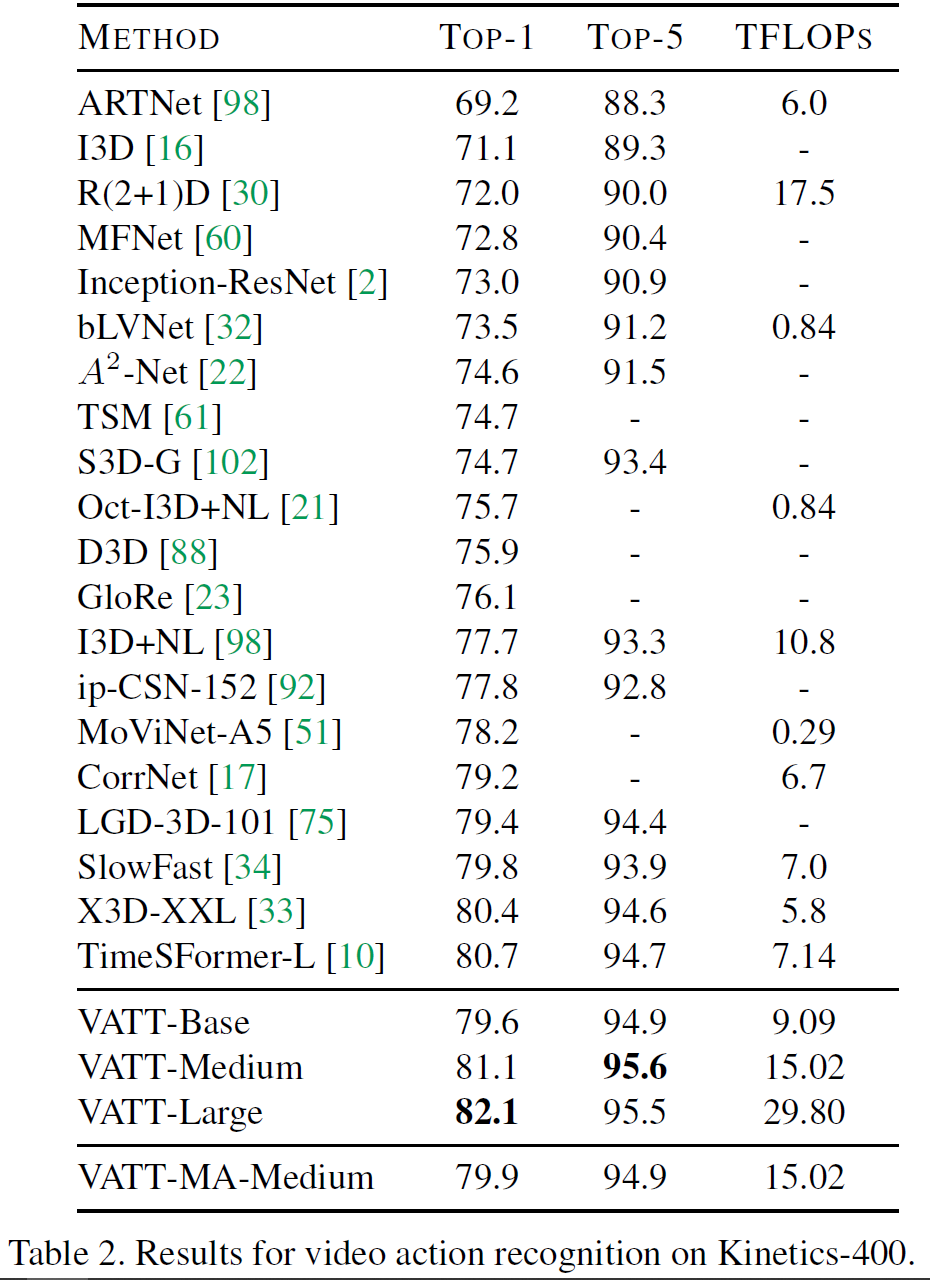
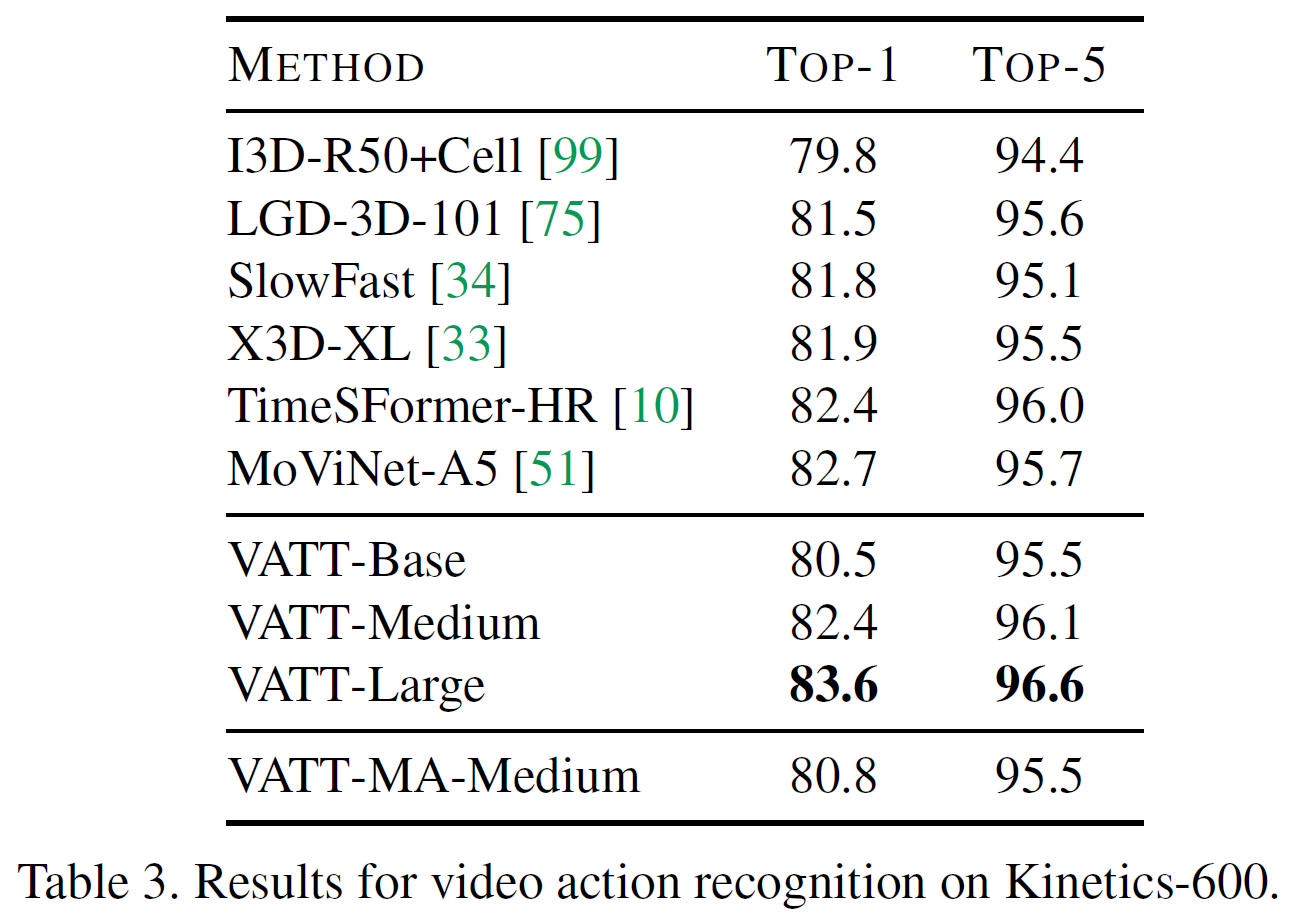
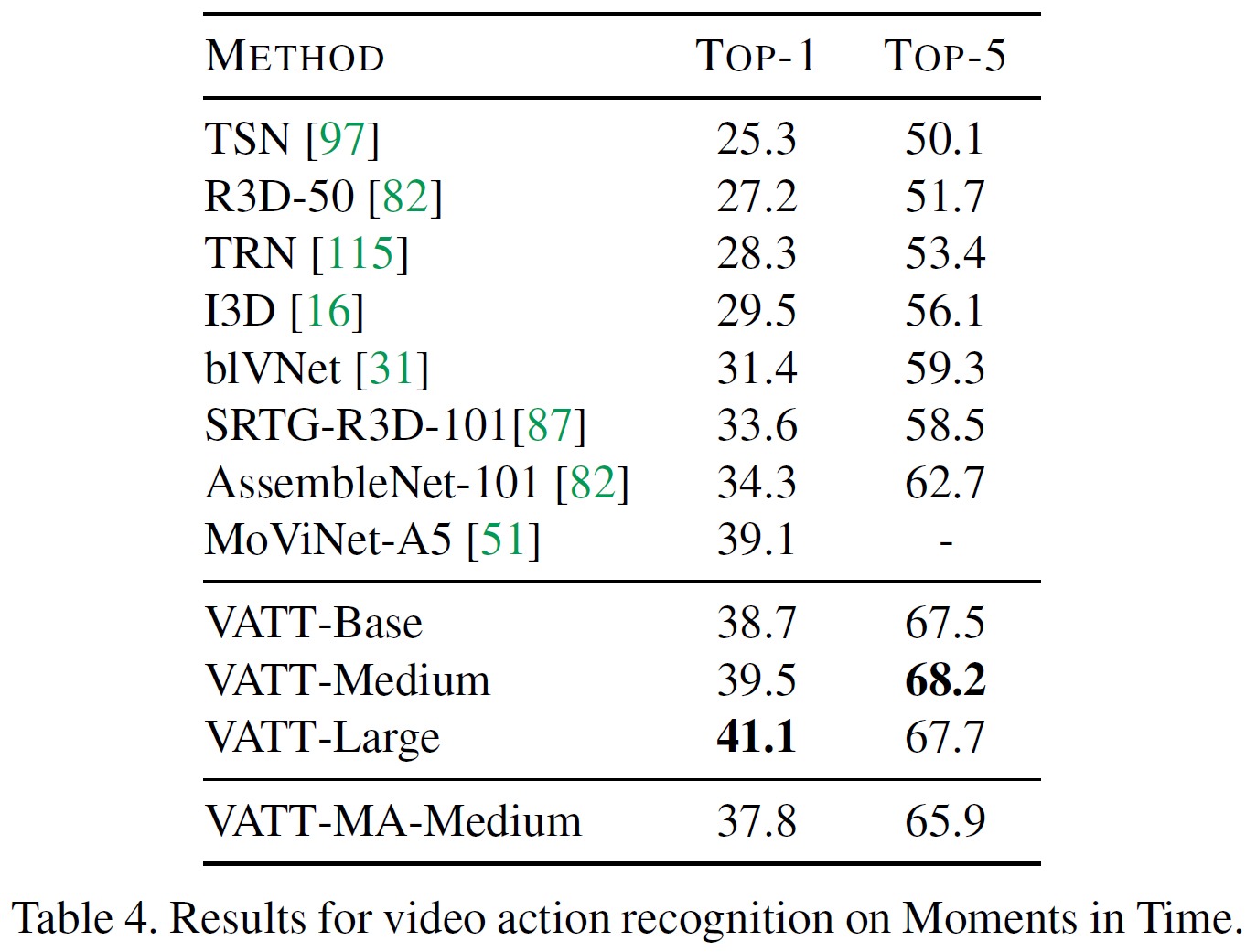
TimeSFormer를 비롯하여 다른 이전 연구들보다 더 높은 정확도를 기록하였음을 볼 수 있다. 본 논문에서 VATT는 multimodal video에서 자기지도를 사용하여 사전학습한 최초의 vision Transformer backbone을 제공하였다고 주장하고 있다. 또한 video action recognition에서 SOTA 결과를 달성하였다.
또한, video, audio, text modality가 공유하는 modality-agnostic backbone 모델인 VATT-MA-Medium는 video action recognition에 최적화된 modality-specific VATT-Base와 비등하다. 이는 하나의 Transformer backbone으로 3개의 modality를 통합할 수 있는 가능성을 보여준다.
4.4.2 Fine-tuning for audio event classification
Multi-label audio event 분류 성능을 평가하는 AudioSet 데이터셋에서 VATT의 audio Transformer를 평가하였다. vision의 것과 비슷하게 마지막 사전학습 checkpoint를 사용한다.
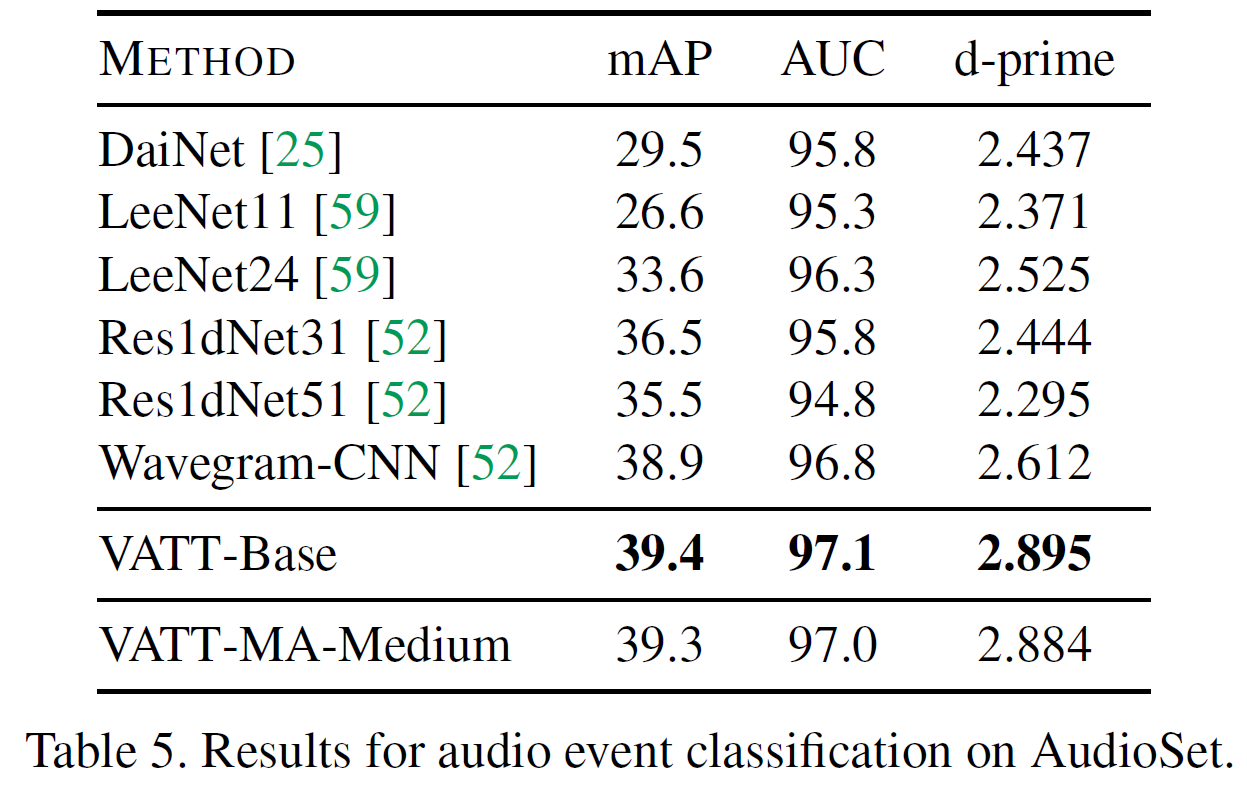
CNN 기반 모델보다 일관되게 좋은 성능을 보여준다. Modality-agnostic인 VATT-MA-Medium의 경우 modality-specific인 VATT-Base와 비등하다. VATT는 raw waveform만 사용하였으며 사람이 만든 어떤 feature도 사용하지 않았다.
4.4.3 Fine-tuning for image classification
multimodal video에서 사전학습된 모델이지만 이미지 영역에서도 그 성능을 측정하고자 한다.
먼저 VATT를 ImageNet에서 사전학습시킨다. 이때 모델 구조는 그대로 두고 이미지를 영상과 같은 형식으로 입력으로 주기 위해 이미지를 4번 복사하여 네트워크에 집어넣는 방식을 사용했다. 그러면 입력은 하나의 video clip처럼 다루게 되고 자기지도 학습을 수행한다.

위의 결과는 VATT가 영상 기반으로 학습한 모델일지라도 이미지 영역에서도 훌륭함을 보여준다.
4.4.4 Zero-shot retrieval
YouCook2와 MSR-VTT에서 평가를 진행하였다. Text query가 주어지면 top-10 영상 중 정답인 영상에 대한 recall을 측정(R@10)했다. 또한 정답 영상의 중간 rank(MedR)도 측정했다.
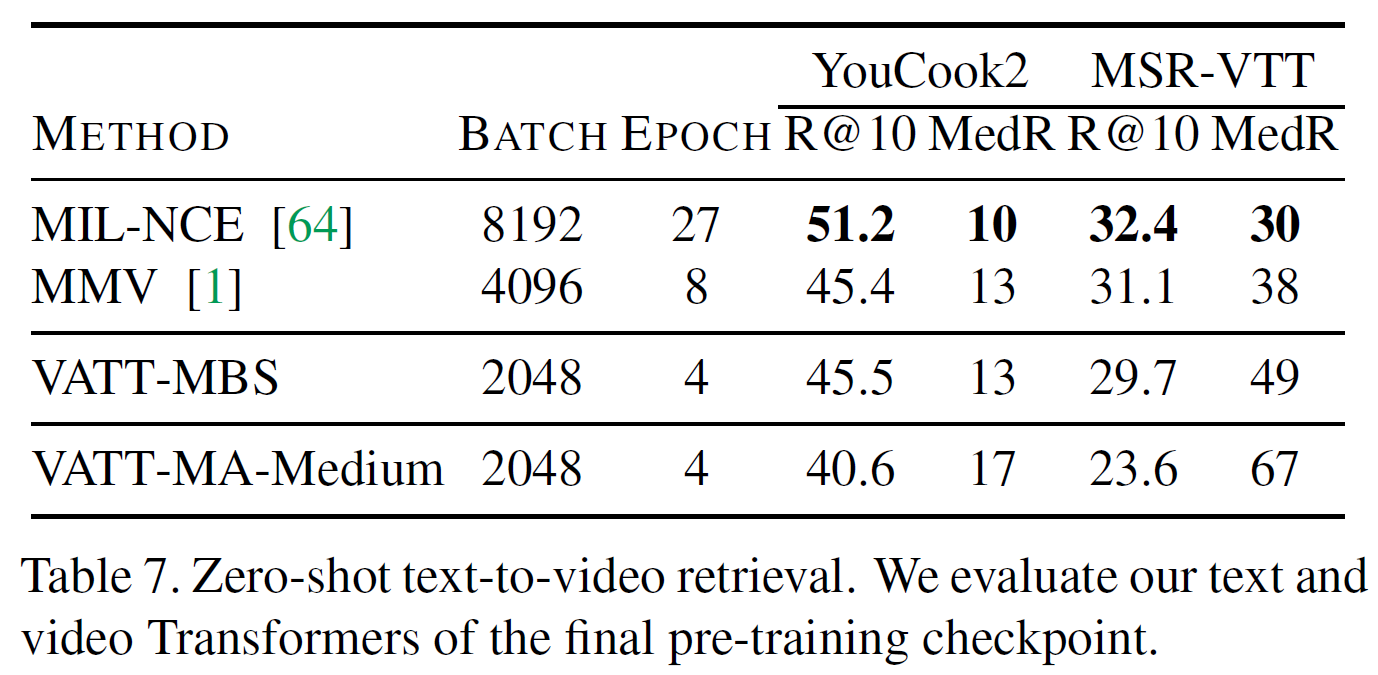
실험 중 batch size와 epoch에 큰 영향을 받는다는 것을 발견하였다. MMV에는 절반의 크기를 사용하는 것이 효과적이었다.
결과를 보면 아마도 텍스트가 noisy하기 때문에 VATT와 같은 복잡한 언어모델이 낮은 평가를 받는 것으로 예상된다고 한다. 단순한 선형전사를 사용하는 것이 여전히 합리적으로 작동한다고 알려져 있다.
4.4.5 Linear evaluation
전체 backbone을 고정시켰을 때 VATT의 일반화 성능을 테스트한다. 여기서, vidoe와 audio modality에 집중하고 고정된 backbone의 출력을 선형분류기로 학습시킨다. 섹션 4.3에서 설명한 LRC(low-rank classifier)에 더해 SVM 분류기 성능을 기술한다. 아래 표에서 3가지 데이터셋에 대한 결과를 볼 수 있다.
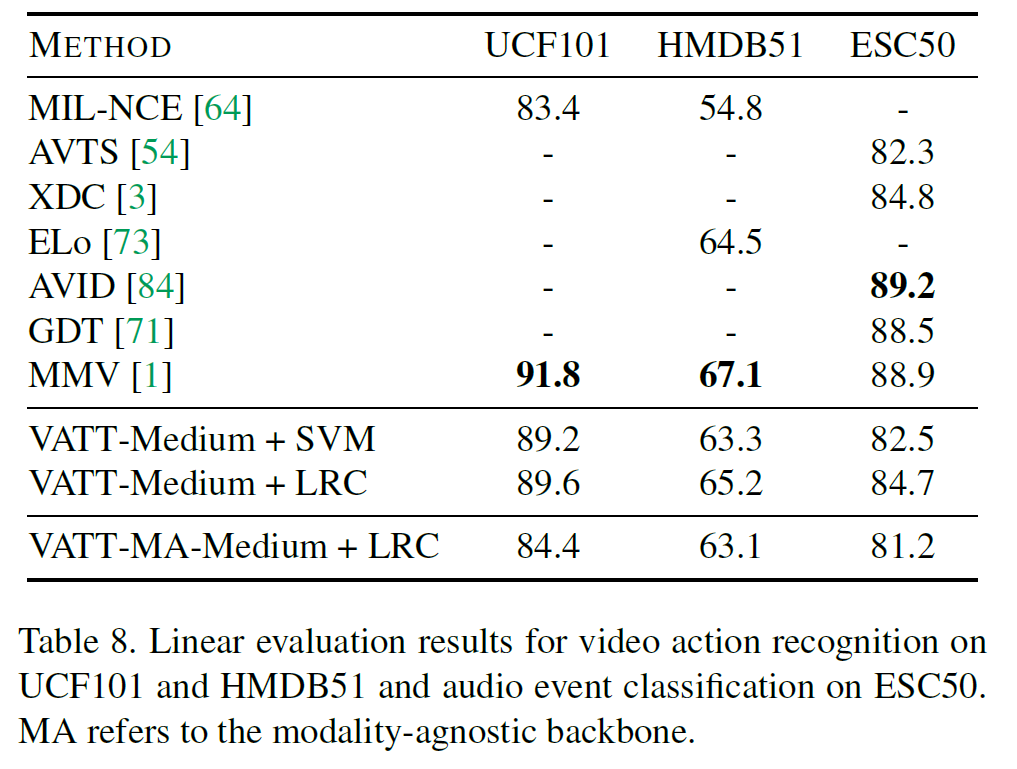
vATT가 가장 좋은 CNN 모델을 이기지는 못했다. 전체적으로, VATT의 backbone은 덜 선형 분리되는(less-linearly-separable) feature를 학습하며, 특히 비선형전사를 포함하는 contrastive estimation head에서 그렇다.
4.4.6 Feature visualization
modality-specific과 modality-agnostic vATT를 Kinetics-400에 미세조정하고 t-SNE를 사용하여 출력 feature 표현을 시각화했다.

그림 3에서, 미세조정된 VATT는 scratch로부터 학습한 모델보다 더 나은 분리 능력을 가지는 것을 볼 수 있다. 또 modality-agnostic과 modality-specific 간에는 별다른 차이가 없다.
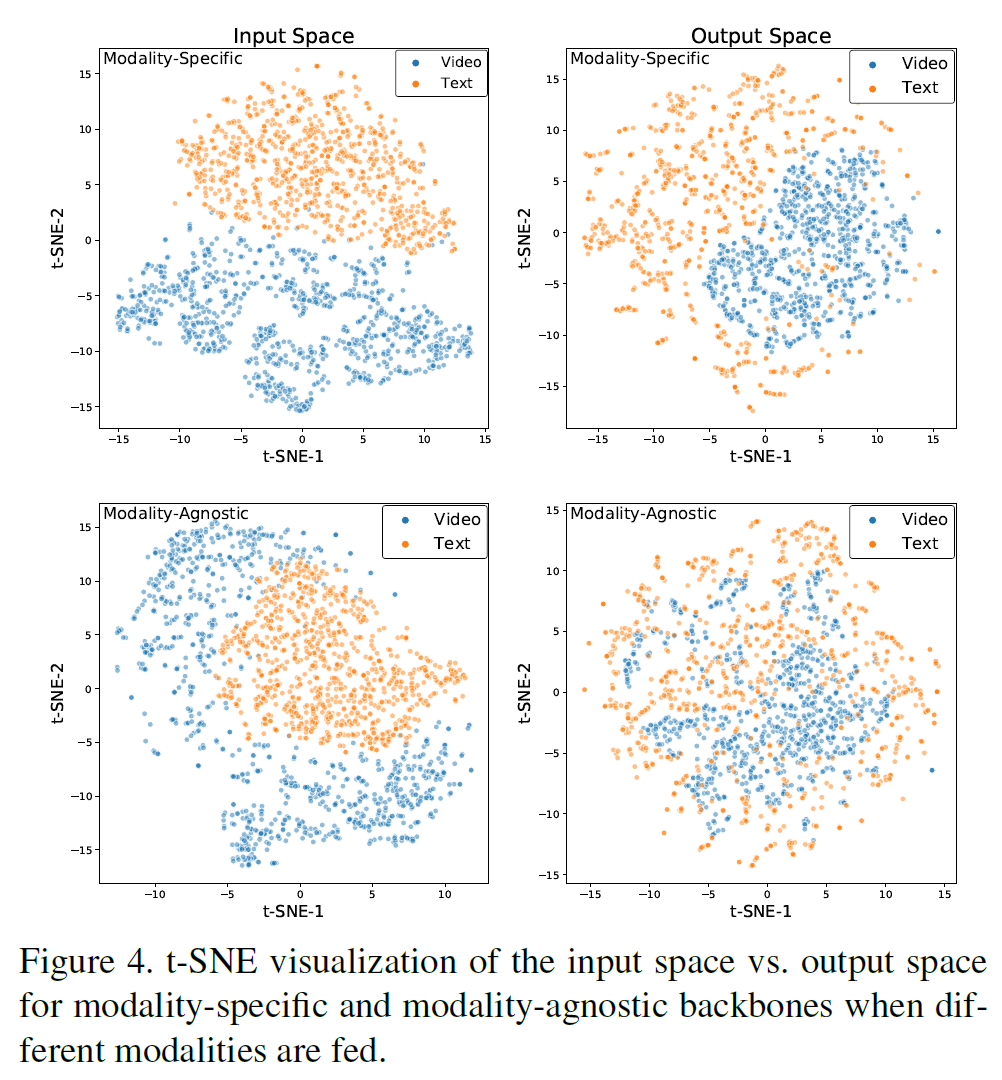
그림 4에서, modality-agnostic 모델의 경우가 좀 더 그 출력 표현이 섞여 있는 것을 볼 수 있다. 이는 modality-agnostic backbone이 같은 concept을 묘사하는 다른 symbol을 다른 modality로 본다는 뜻이다. 이는 여러 언어를 지원하는 통합 자연어처리 모델과 유사하다.
VATT가 positive video-text 쌍을 어떻게 잘 구별하는지 확인하기 위해, pair-wise 유사도를 모든 가능한 쌍에 대해 계산하고 Kernel Density Estimation(KDE)를 사용하여 시각화했다.
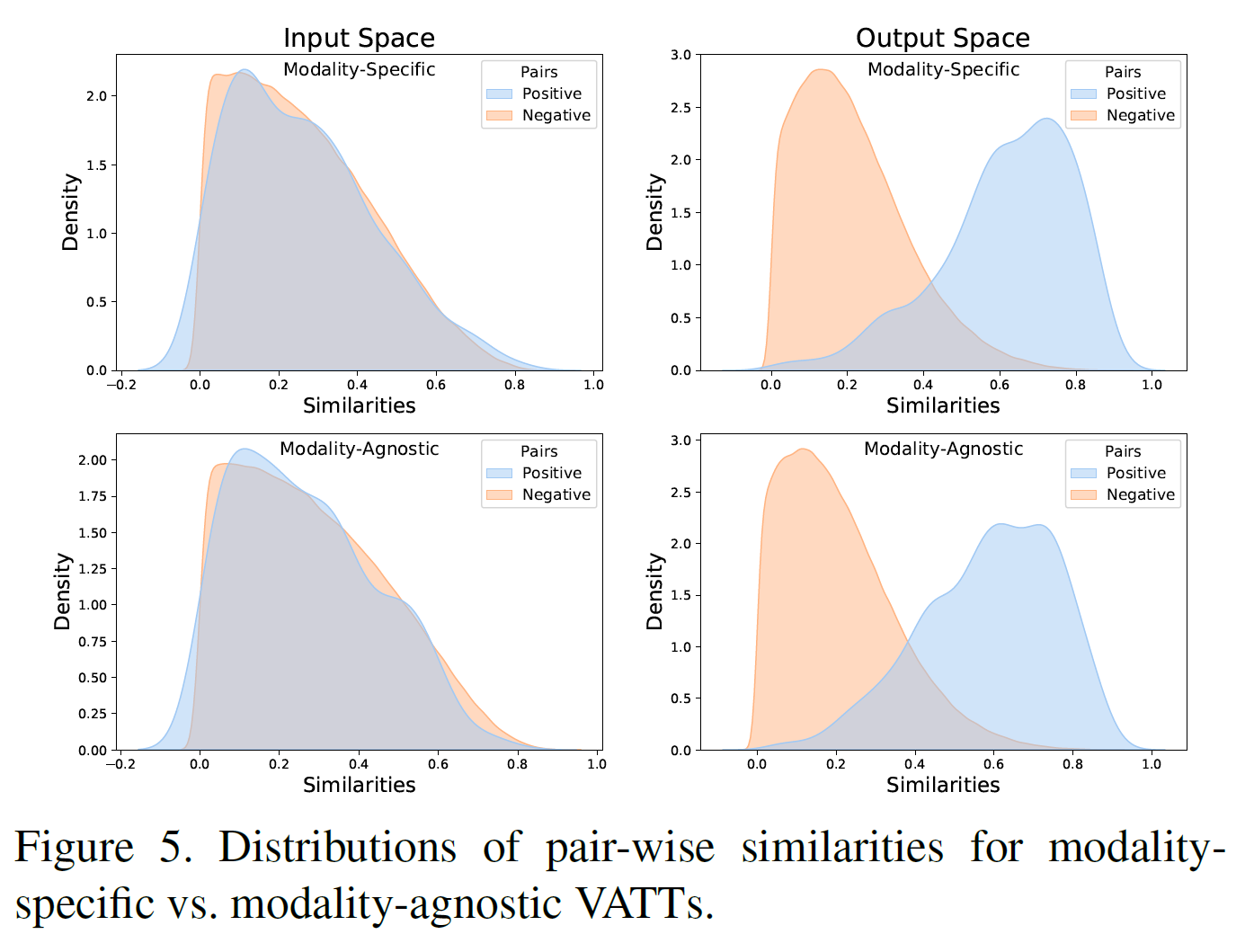
modality-specific/agnostic VATT 둘 모두 잘 구분해 내는 것을 볼 수 있다.
4.5. Ablation study
VATT가 raw multimodal signal을 입력으로 받기 때문에 입력 크기와 어떻게 patch되는지 등이 최종 성능에 큰 영향을 끼친다. 먼저 patch 크기를 $5 \times 16 \times 16$으로 고정하고 각 video clip당 frame crop size와 샘플링되는 frame 수를 변화시켜 보았다.
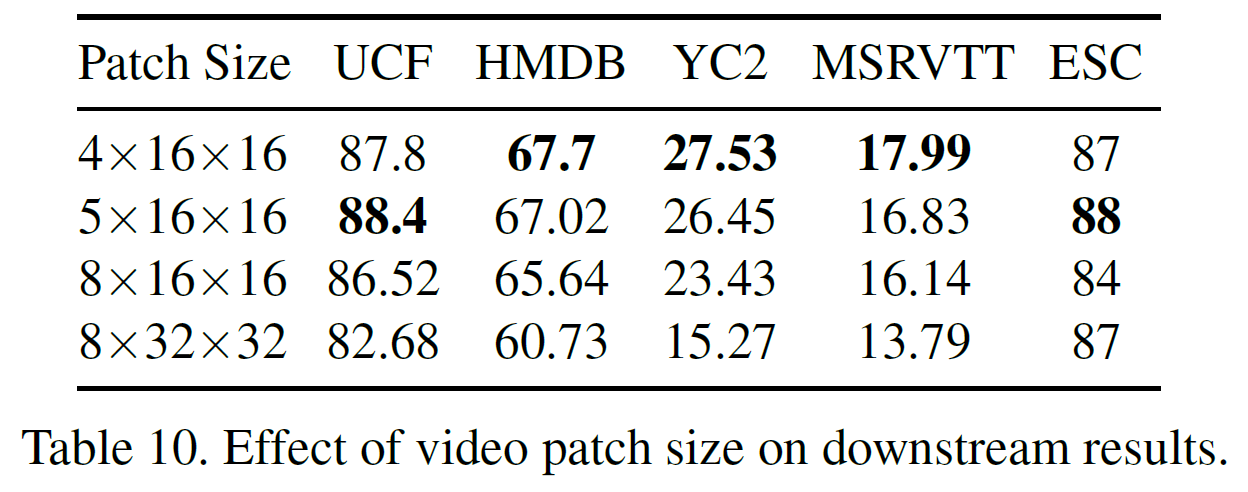
크기가 $4 \times 16 \times 16$ 이하인 경우는 계산시간이 많이 증가하여 제외하였다.
patch size를 다르게 했을 때 결과는 아래와 같다. 128일 때가 가장 좋다.
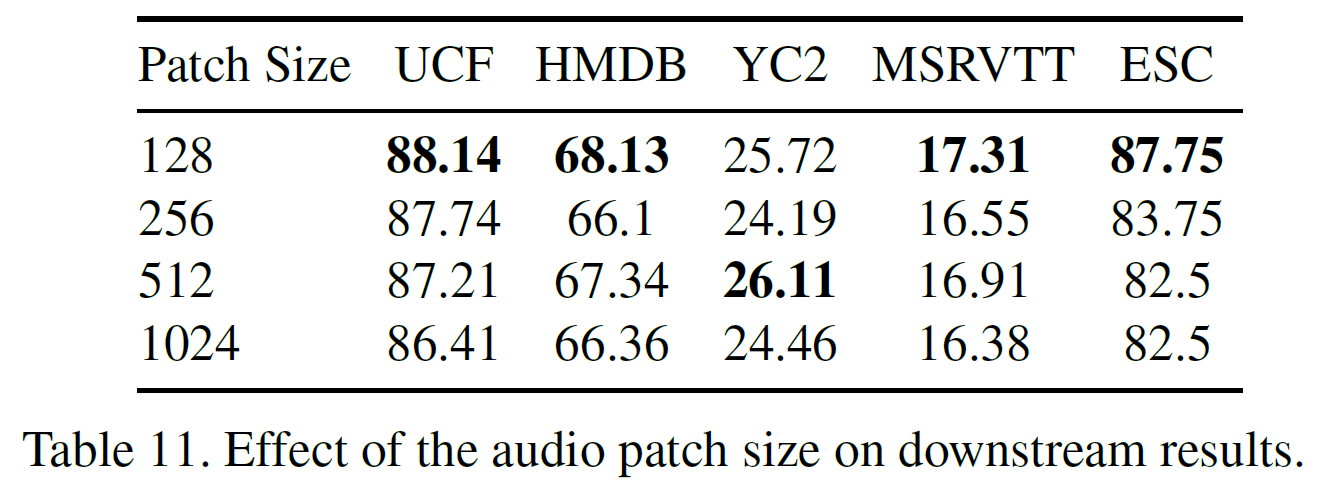
audio를 waveform 형태로 할지, spectrogram 형태로 할지는 아래 결과에 나와 있다. raw waveform이 유용할 수 있음을 보인다.
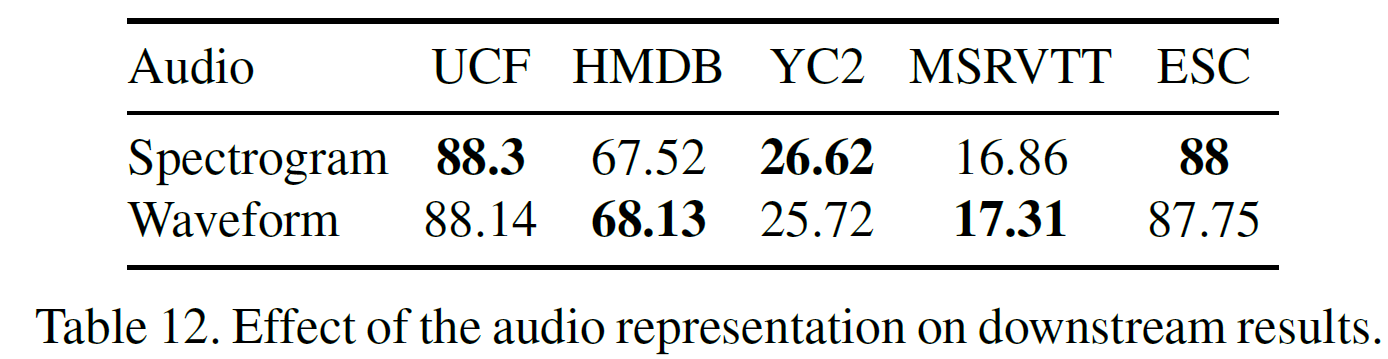
4.5.2 DropToken
frame이나 waveform의 일정 비율을 임의로 drop하여 입력으로 주는 방법의 성능 및 학습시간을 평가한다. 이렇게 drop하는 비율을 각각 75%, 50%, 25%, 0%일 때를 나누어 계산량과 성능을 평가하였다.
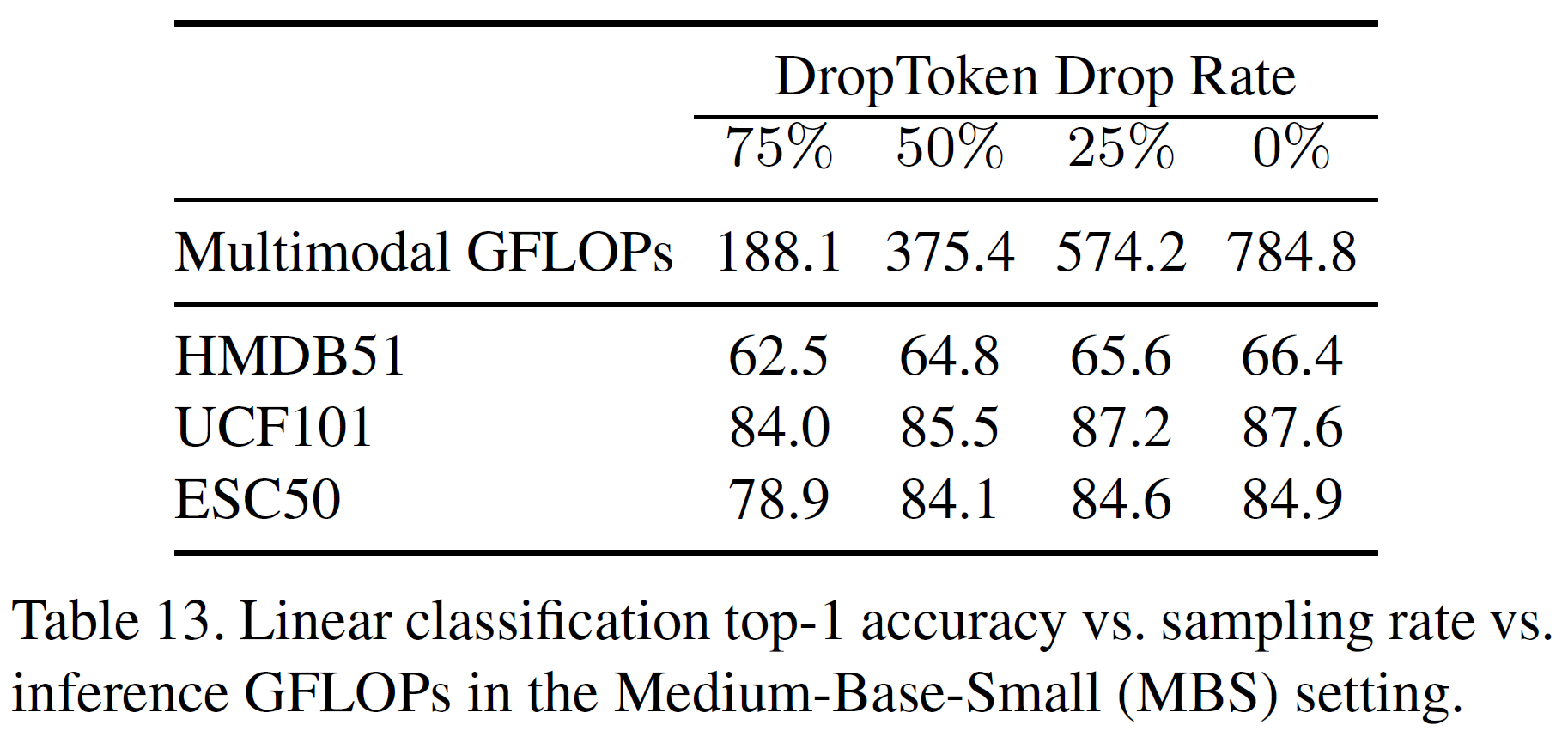
위의 표를 보면 50%인 경우가 계산량 대비 가장 좋은 성능을 갖추었다고 말할 수 있다. 아래는 DropToken 방식과 해상도 조절 방식을 비교한 표이다.
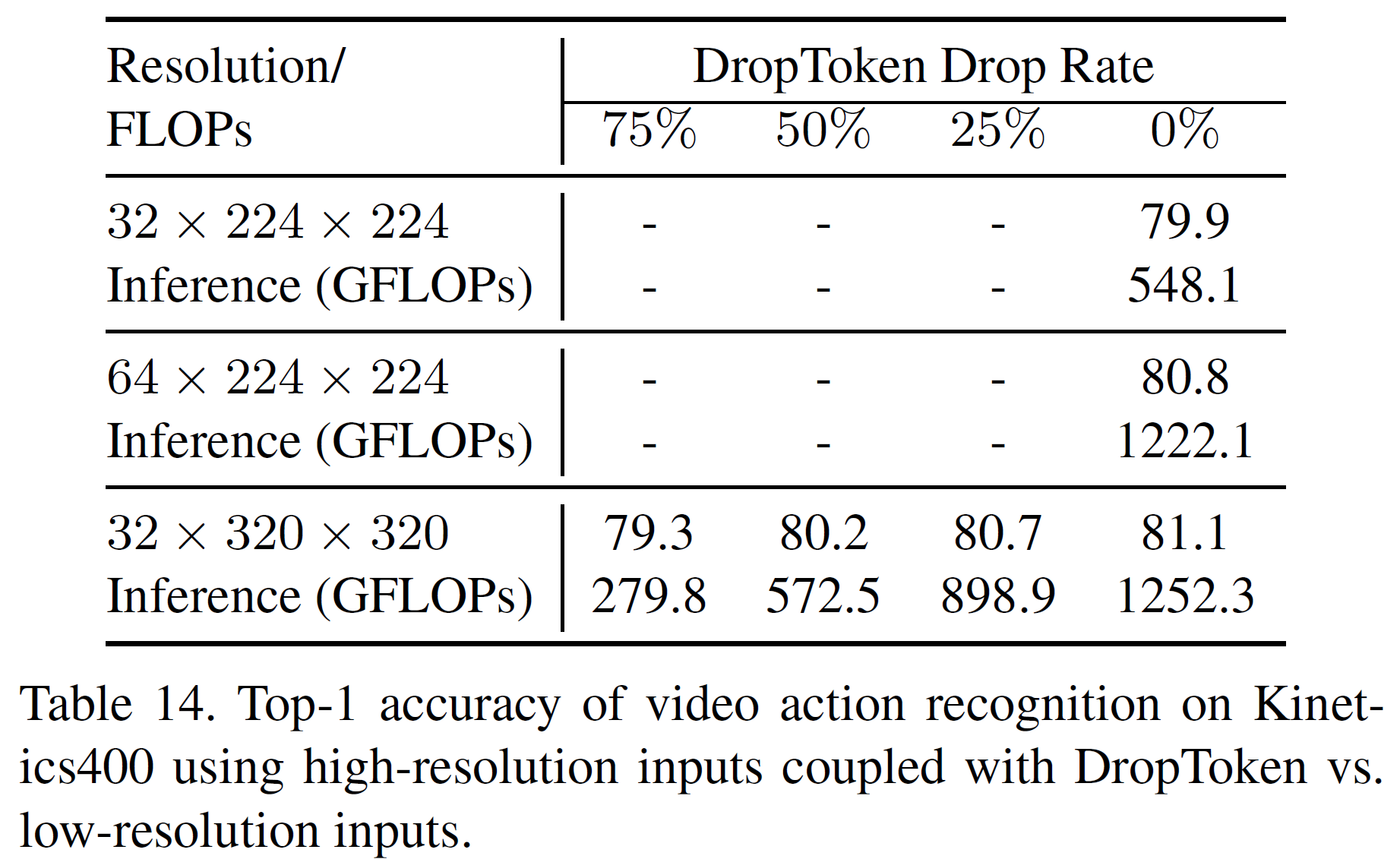
DropToken이 계산량 대비 성능이 해상도를 낮추는 방식과 비슷하거나 더 나은 것을 밝혔다.
5. 결론(Conclusion)
Transformer에 기반한 자기지도 multimodal 표현 학습 framework를 본 논문에서 제안하였다. Multimodal 영상 입력에서 작동하는 순수 attention 기반 모델과 함께, 본 연구는 대규모 자기지도 사전학습이 Transformer 구조의 데이터 부족 문제를 해결하면서 여러 downstream task에서 CNN과 비교해 성능이 좋다는 것을 밝혔다. 또한 간단하지만 효과적인 방식 DropToken을 사용하여 입력 길이의 제곱에 비례하는 Transformer의 연산량을 획기적으로 줄여 계산량 대비 성능을 끌어올렸다.
그리고 여러 downstream task에서 좋은 성능을 거두었고 일반적인 multimodal 모델을 개발하는 포문을 열었다. 추후에는 Transformer를 학습시키는 데이터 증강기법과 다양한 multimodal task에서 modality-agnostic backbone을 적절히 정규화하는 방법을 연구할 계획이다.
참고문헌(References)
논문 참조!