이 글에서는 Baidu에서 만든 모델 시리즈 ERNIE 중 두 번째(ERNIE 2.0: A Continual Pre-Training Framework for Language Understanding)를 살펴보고자 한다.

ERNIE 시리즈는 다음과 같다. 참고로 2번째는 Baidu가 아닌 Tshinghus University에서 발표한 논문이다.

• ERNIE: Enhanced Representation through Knowledge Integration, Yu sun el al., 2019년 4월
• ERNIE 2.0: A Continual Pre-training Framework for Language Understanding, Yu Sun et al., 2019년 6월
• ERNIE-ViL: Knowledge Enhanced Vision-Language Representations Through Scene Graph, Fei Yu et al., 2019년 6월
• ERNIE-Doc: A Retrospective Long-Document Modeling Transformer, Siyu Ding et al., 2020년 12월
• ERNIE 3.0: Large-Scale Knowledge Enhanced Pre-Training For Language Understanding And Generation, Yu Sun et al., 2021년 7월

중요한 부분만 적을 예정이므로 전체가 궁금하면 원 논문을 찾아 읽어보면 된다.

ERNIE 2.0: A Continual Pre-Training Framework for Language Understanding

논문 링크: ERNIE 2.0: A Continual Pre-training Framework for Language Understanding

Official Code: Github

초록(Abstract)

최근 사전학습 모델들이 다양한 언어이해 문제에서 SOTA 결과를 달성해 왔다. 현재 사전학습 과정은 보통 모델을 여러 개의 단순한 task에서 학습시켜 단어나 문장의 동시 등장(co-occurrence)을 학습하는 것에 주안점을 둔다. 그러나, 이러한 동시등장성 외에도 다른 귀중한 정보인 named entity, 의미적 유사성, 담화 관계 등 어휘적, 구문, 의미적 정보가 학습 말뭉치에 존재한다. 이러한 정보를 추출하고 학습하기 위해서 사전학습 task를 점진적으로 증가시키고 연속적 multi-task 학습을 통해 이들 task에서 모델을 사전학습시키는 연속적 사전학습 framework인 ERNIE 2.0을 본 눈문에서 제안한다. 이 framework에 기반하여, 여러 task를 만들고 ERNIE 2.0을 학습시켜 영어(GLUE) 및 중국어 문제 총 16개의 task에서 BERT와 XLNet을 능가함을 보였다.

1. 서론(Introduction)

ELMo, OpenAI GPT, BERT, ERNIE 1.0, XLNet 등의 사전학습 언어표현은 감정분류, 자연어추론, 명명 객체 인식 등 다양한 자연어이해 문제에서 성능을 향상시킬 수 있다는 것이 입증되었다.

일반적으로 모델의 사전학습은 단어와 문장의 co-occurrence에 기반하여 모델을 학습시킨다. 그러나, 문장에는 사실 어휘적, 구문, 문맥적 정보가 존재하며 때로 이 정보가 더 중요할 수도 있다. 예를 들어 사람/지명 이름 등은 개념적 정보를 담고 있을 수 있다. 문장 순서나 문장의 유사성 등은 모델이 구조정보가 포함된 표현을 학습하는 것을 가능하게 한다. 그리고 문서 수준 의미적 유사성 혹은 문장 간 담화 관계는 모델이 의미정보가 포함된 표현을 학습할 수 있게 한다. 학습 말뭉치로부터 이러한 귀중한 정보를 활용하기 위해 연속적 사전학습 framework인 ERNIE 2.0을 제안한다.

ERNIE framework는 continual multk-task 학습 방식을 통해 다양한 customized task를 연속적으로 사용할 수 있다. 하나 혹은 여러 개의 새로운 task가 주어지면, 연속적 multi-task 학습 방식은 기존 지식을 잊어버리지 않으면서도 새로 소개된 task를 기존 task와 동시에 학습시킨다. 이러한 방식으로, ERNIE framework는 분산표현을 계속하여 학습할 수 있으며 모든 task는 같은 encoding network를 공유하여 이 인코딩의 어휘적, 구문, 의미적 정보가 여러 task 사이에서 공유되는 것을 가능하게 한다.

요약하면, 이 논문이 기여한 바는:

1. customized 학습 task와 연속적 multi-task 학습 방식을 효과적으로 지원하는 ERNIE 2.0 framework를 제안하였다.
2. 3가지의 비지도학습 task를 만들어 제안된 framework의 효율성을 확인하였다. 실험 결과는 ERNIE 2.0이 영어(GLUE)와 여러 중국어 task에서 BERT와 XLNet을 능가함을 보여주었다.
3. ERNIE 2.0의 미세조정 코드와 모델을 Github에서 볼 수 있다.

2. 관련 연구(Related Work)

Unsupervised Learning for Language Representation

Annotation이 없는 많은 양의 데이터로 언어모델을 사전학습시켜 일반적인 언어표현을 학습하는 것은 효과적이다. 전통적인 방법은 보통 문맥무관 단어 임베딩에 초점을 두었다. Word2Vec과 GloVe가 단어별로 고정된 임베딩을 학습하는 대표적인 방식이다.

최근, 문맥 의존 언어표현을 학습하는 방식이 많이 연구되었다.

• ELMo는 언어모델에서 문맥민감(context-sensitive) 특징을 추출하는 방식을 제안하였고,
• OpenAI GPT는 Transformer를 수정하여 문맥민감 임베딩을 발전시켰다.
• BERT는 사전학습으로 다음 문장 예측 task를 추가하여 masked 언어모델을 만들었다.
• XLM은 교차 언어(cross-lingual) 언어모델을 학습하기 위해 1) 단일 언어 데이터에 의존하는 비지도학습 2) 2개의 언어 데이터를 leverage하는 지도학습 두 가지 방식을 결합하였다.
• MT-DNN은 여러 지도학습 방식을 사용하여 GLUE에서 좋은 결과를 냈으며,
• XLNet은 Transformer-XL을 사용하여 우도를 최대화하는 양방향 문맥을 학습하는 일반화된 자동회귀 사전학습 방식을 제안하였다.

Continual Learning

연속적 학습(continual learning)은 모델이 여러 task를 차례로 학습하도록 하되 새로 학습하면서 이전 학습한 task를 잊어버리지 않도록 하는 것을 목표로 한다. 이러한 방법은 계속해서 학습하고 정보와 지식을 쌓아가는 사람의 학습 방식에서 영감을 받은 것으로, 이러한 연속적 학습을 통해 모델은 이전 학습에서 얻은 지식을 활용하여 새로운 task에서도 좋은 성능을 발휘할 것으로 기대된다.

3. The ERNIE 2.0 Framework

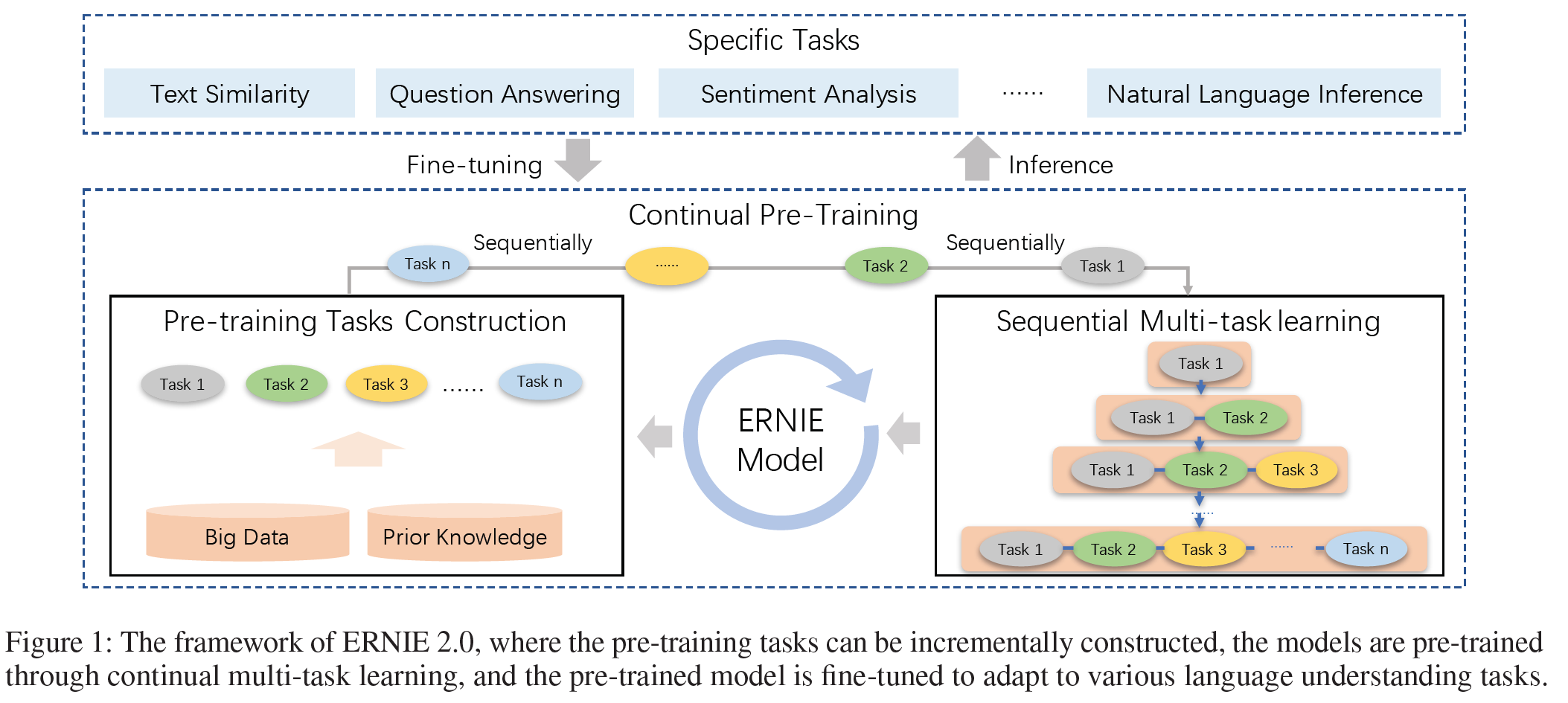
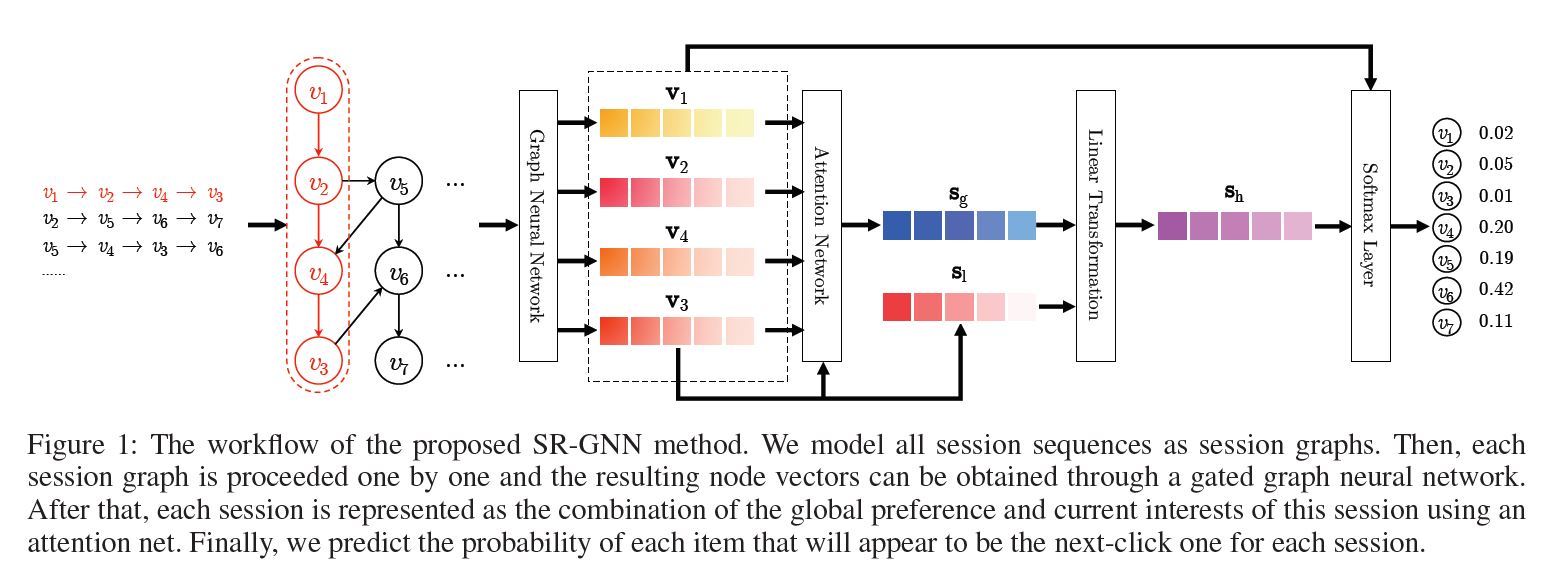
위 그림 1에서 보듯이 ERNIE 2.0은 널리 쓰이는 사전학습-미세조정 구조에 기초한다. 다른 점은 사전학습 단계에서 적은 수의 목적함수 대신 더 광범위한 사전학습 task를 사용하여 모델이 효율적으로 어휘적, 문맥적, 의미적 표현을 학습할 수 있도록 한 것이다. 이에 기초하여 ERNIE 2.0은 연속적 multi-task 학습을 통해 사전학습 모델을 업데이트할 수 있게 한다. 미세조정 단계에서 ERNIE는 먼저 사전학습 parameter를 사용하여 초기화한 다음 특정 task에 대해 미세조정하게 된다.

Continual Pre-training

연속적 사전학습은 두 단계로 이루어진다.

1. 많은 데이터와 사전지식이 포함되도록 비지도 사전학습 task를 구성한다.
2. ERNIE를 연속적 multi-task 학습을 통해 점진적으로 학습시킨다.

Fine-tuning for Application Tasks

각 단계에서 다른 종류의 task(word/structure/semantic - aware task)를 구성한다. 모든 사전학습 task는 자기지도 또는 약한 지도 signal에 의존하여 annotation 없이 대규모 데이터로부터 얻을 수 있다. 명명 객체나 구, 담화 관계와 같은 사전 지식은 대규모 데이터로부터 label을 생성하는 데 쓰인다.

Continual Multi-task Learning

ERNIE 2.0은 여러 개의 다른 task로부터 어휘적, 문맥적, 의미적 정보를 학습하는 것을 목표로 한다. 따라서 극복해야 할 두 가지 문제가 있다.

1. 이전에 학습한 지식을 잊어버리지 않으면서 학습을 연속적으로 할 수 있을지
2. 어떻게 효율적으로 사전학습할 것인지

이를 해결하기 위해 연속적 multi-task 학습 방법을 제안한다. 새로운 task를 만나면, 연속적 multi-task 학습 방법은 먼저 이전 학습된 parameter를 사용하고, 원래 학습하던 task와 새로운 task를 동시에 사용하여 학습한다. 이는 학습된 parameter가 이미 학습된 지식을 encode하도록 할 수 있다. 남은 문제는 효율적으로 학습할 방법인데, 이는 각 학습 task마다 $N$번의 반복학습을 배정함으로써 해결했다. 이러한 $N$번의 반복을 task에 자동으로 배정할 것을 필요로 하는데 이러한 방법을 통해 모델이 이전 지식을 잊어버리지 않도록 할 수 있다.

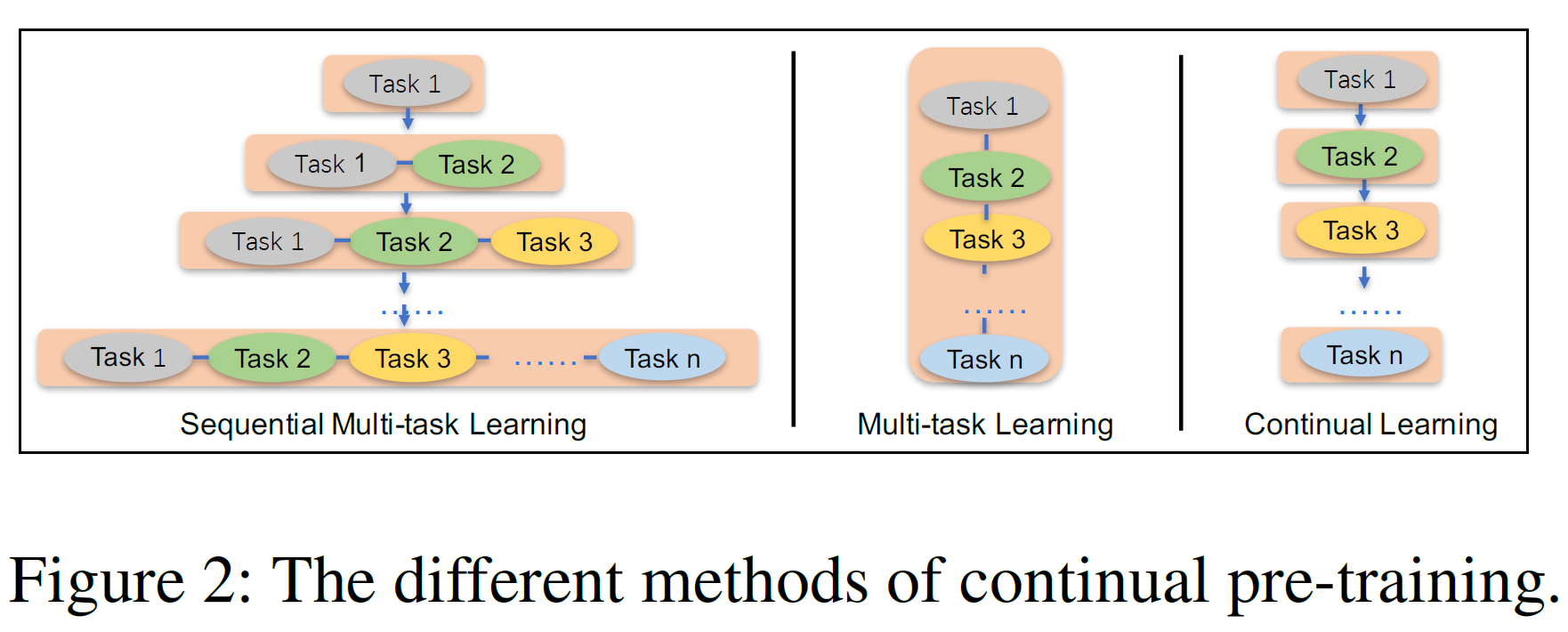
위 그림은 ERNIE와 기존의 multi-task 학습 및 연속학습 모델과의 차이를 보여준다. Scratch로부터 학습하는 Multi-task 학습은 같은 시간에 여러 개의 task를 학습할 수 있으나 모두 customized된 사전학습 task가 준비되어야 한다. 따라서 이 방법은 연속학습 이상의 학습 시간을 필요로 한다. 전통적인 연속학습 방법은 모델이 각 단계에서 오직 하나의 task만을 학습하는 문제가 있고 또한 그 구조상 이전 학습에서 얻은 지식을 잊어버릴 수 있다.

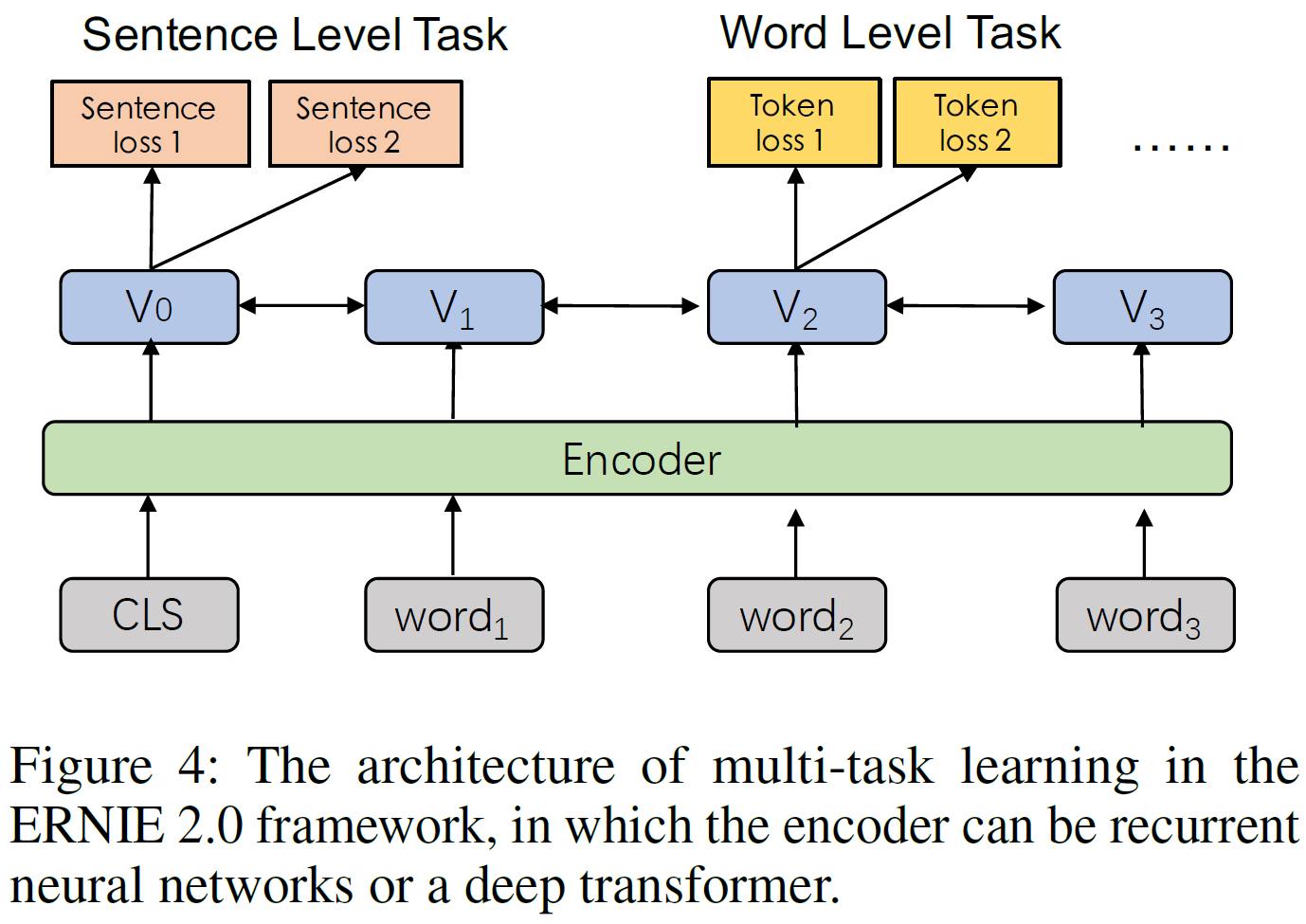
위의 그림에서 연속적 multi-task 학습의 각 단계가 문맥 정보를 인코딩하는 여러 개의 공유된 text encoding layer를 포함하고 있고 이는 RNN 혹은 deep Transformer를 통해 customized될 수 있다. 인코더의 parameter는 모든 학습 task에서 업데이트될 수 있다.

이 framework에서는 BERT와 비슷하게 두 가지 손실함수가 존재한다.

1. 문장 수준 loss
2. token 수준 loss

각 사전학습 task는 고유한 손실함수를 갖는다. 사전학습하는 동안, 하나의 문장수준 손실함수는 모델을 연속적으로 업데이트하기 위해 여러 개의 token 수준 손실함수와 결합될 수 있다.

Fine-tuning for Application Tasks

Task-specific 지도 데이터에서 사전학습의 장점은, 사전학습 모델은 여러 언어의 이해 task(예. QA, 자연어추론, 의미적 유사성 task)에 적용될 수 있다는 것이다. 각각의 downstream task는 미세조정 이후 고유한 미세조정 모델을 갖는다.

4. ERNIE 2.0 Model

이 framework의 효율성을 검증하기 위해 3가지의 비지도 언어처리 task를 구성하고 사전학습 모델 ERNIE 2.0을 개발하였다. 이 섹션에서 모델의 구현 방법을 설명한다.

Model Structure

Transformer Encoder 이 모델은 GPT나 BERT, XLM과 비슷하게 multi-layer Transformer를 기본 인코더로 사용한다.
Transformer는 self-attention을 통해 sequence에서 각 token의 문맥 정보를 잡아낼 수 있으며 문맥 임베딩의 sequence를 생성할 수 있다. Sequence가 주어지면 [CLS]를 맨 앞에 추가하고 여러 개의 입력이 들어오는 경우 구분을 위해 그 사이에 [SEP] token을 추가한다.

Taxk Embedding 모델은 서로 다른 task의 특성을 표현하기 위해 task embedding을 입력받는다. Task들은 각각 $0 \sim N$의 번호를 부여받으며 고유한 embedding을 갖는다. 이에 대응되는 token, segment, position, task embedding은 모델의 입력으로 사용된다. 각 task id를 미세조정 단계에서 모델을 초기화하는 데 사용한다. 모델 구조는 아래와 같다.

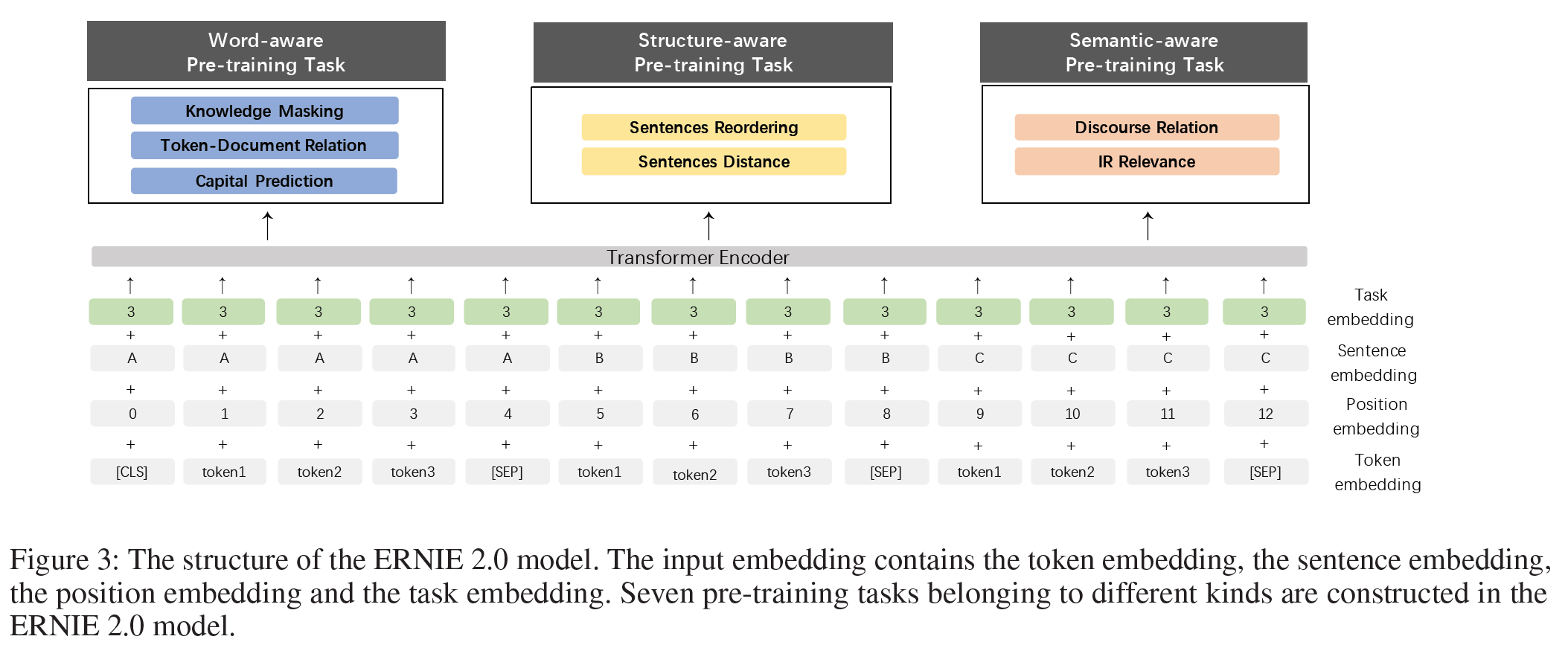
Pre-training Tasks

3가지의 사전학습 task를 구성하여 학습 데이터로부터 서로 다른 정보를 가져올 수 있도록 했다. 단어수준 task는 모델이 어휘적 정보를, 문장수준 task에서는 말뭉치의 구문 정보를, 의미수준 task는 의미정보를 가져오는 것에 초점을 둔다.

Work-aware Pre-training Tasks

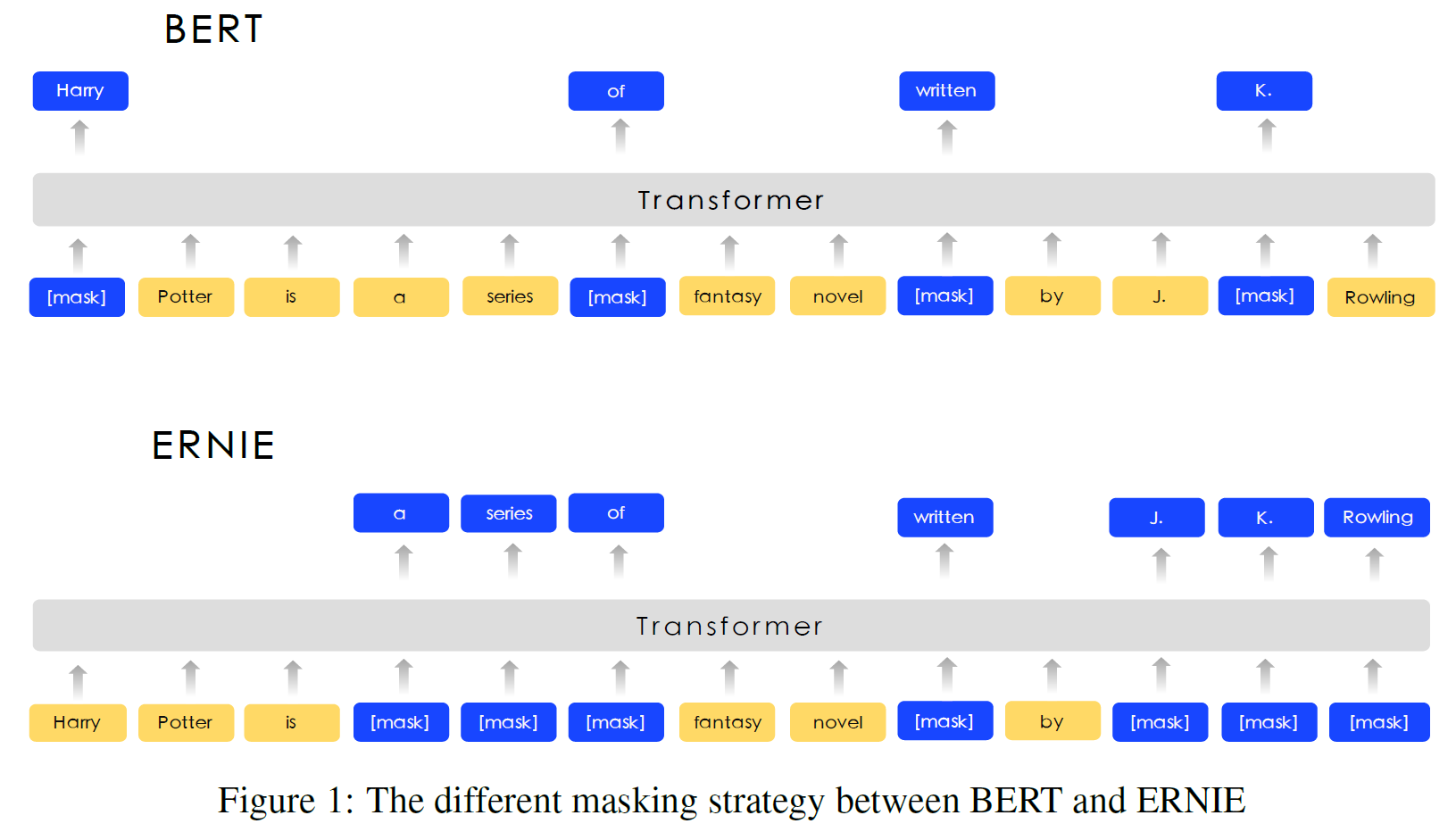
1. Knowledge Masking Task: ERNIE 1.0에서는 지식통합을 통해 표현의 질을 높이는 효과적인 방법을 제시하였다. phrase 및 명명 객체 전체의 masking과 masking된 전체 부분을 예측하는 task를 도입함으로써 지역적 및 전반적인 문맥에서의 의존 정보를 학습할 수 있게 하였다. 이를 ERNIE 2.0 모델의 초기 버전으로 학습하도록 하였다.
2. Capitalization Prediction Task: 전체가 대문자로 쓰여진 단어는 보통 특별한 의미를 담고 있다. 이러한 경우 모델은 명명 객체 인식과 같은 문제에서 이점을 가지며 이를 고려하지 않는 모델은 다른 task에 더 적합하다. 두 모델의 장점을 합쳐서 어떤 단어가 대문자화된 단어인지 아닌지를 판별하는 task를 추가했다.
3. Token-Document Relation Prediction Task: 이 task는 어느 segment의 token이 원본 문서의 다른 segment에 나타나는지를 예측하는 task이다. 경험적으로, 문서의 많은 부분에서 등장하는 단어는 보통 사용 빈도 자체가 높은 단어이거나 문서의 주요 주제와 관련이 있다. 따라서, 문서에서 자주 등장하는 단어를 판별하는 것을 통해 모델이 문서의 keyword를 찾는 능력을 증대시켜줄 수 있다.

Structure-aware Pre-training Tasks

1. Sentence Reordering Task: 이 task는 문장 간의 관계를 학습하는 데 주안점을 둔다. 이 task의 사전학습 단계 동안 주어진 문단은 $1 \sim m$개의 segment로 임의로 쪼개어 이들 permutation의 모든 조합(combination) 중 하나로 섞는다. 사전학습 모델은 이 segment들의 원래 순서를 찾는 것이 목적이다. 경험적으로 이 문장 재배치 task는 사전학습이 문서 내 문장 간 관계를 학습할 수 있게 한다.
2. Sentence Distance Task: 문서 수준 정보를 사용하여 문장 간 거리를 학습하는 task이다. 3-class 분류 문제로 모델링되는데, 0은 두 문장이 같은 문서에서 인접해 있는 것, 1은 두 문장이 같은 문서에 있는 것, 2는 두 문장이 서로 다른 문서에 존재함을 나타낸다.

Semantic-aware Pre-training Tasks

1. Discourse Relation Task: 위에서 언급한 거리 (측정) 문제에 더하여, 두 문장 간 의미적 혹은 수사적인 관계를 예측하는 task를 소개한다. 영어 task를 위한 사전학습 모델을 학습시키기 위한 데이터를 사용하였다. 같은 논문에서 제안된 방법을 따라 사전학습을 위한 중국어 데이터셋을 구성하였다.
2. IR Relevance Task: 정보 검색에서 짧은 텍스트 관계를 학습하는 사전학습 task를 추가하였다. Query를 첫 번째 문장, title을 두 번째 문장으로 구성하며 상업 검색엔진에서 얻은 검색 기록 데이터를 사전학습 데이터로 사용하였다. 이 task는 3-class 분류 문제로 query과 title 간 관계를 예측한다. 0은 강한 관계(유저가 검색 후 제목을 클릭함), 1은 약한 관계(제목이 검색 결과로 나왔지만 유저가 클릭하지는 않음), 2는 query와 title이 무관하며 의미 정보의 관점에서 임의(로 선택됨)임을 나타낸다.

Experiments

ERNIE 2.0을 다른 SOTA 모델들과 비교하였다. 영어 task를 위해 GLUE에서 BERT 및 XLNet, 중국어 task를 위해 여러 task에서 BERT와 ERNIE 1.0과 비교하였다. 또한 본 논문의 방법을 multi-task 학습과 전통적인 연속학습 방법과 비교하였다.

Pre-training and Implementation

Pre-training Data: BERT와 비슷하게 일부 영어 말뭉치는 Wikipedia와 Book-Corpus에서 크롤링하여 가져왔다. 또한 Reddit과 Discovery data를 담화 관계 데이터로 사용하였다. 중국어 말뭉치는 검색 엔진으로부터 백과사전, 뉴스, 대화, 정보검색, 담화관계 데이터 등을 수집하였다. 표 1에서 사전학습 task와 데이터의 관계를, 데이터의 세부 정보를 표2에 기술하였다.

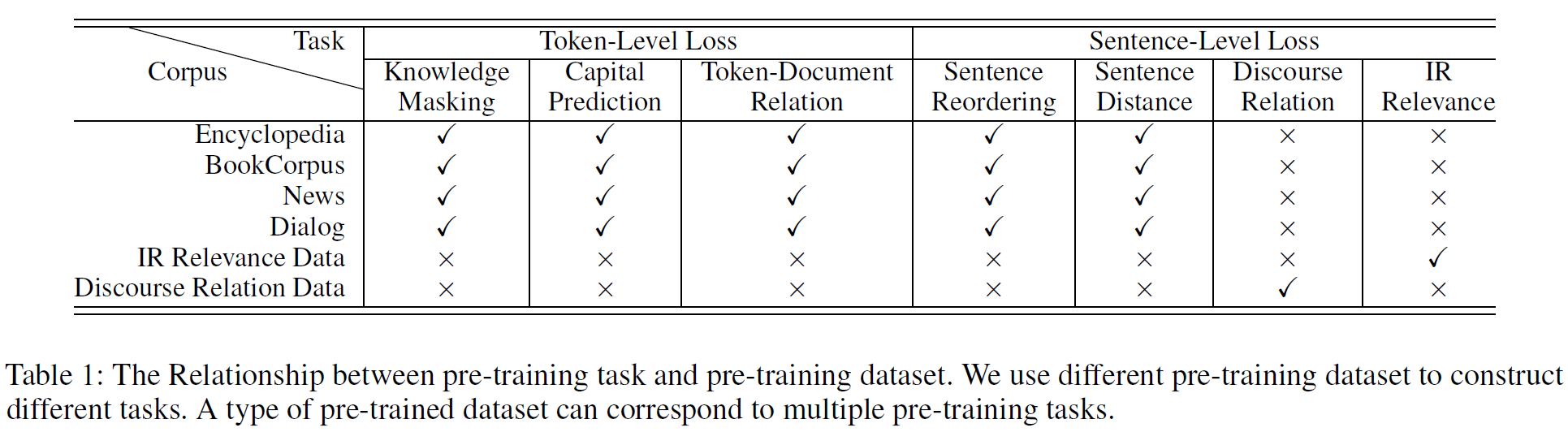
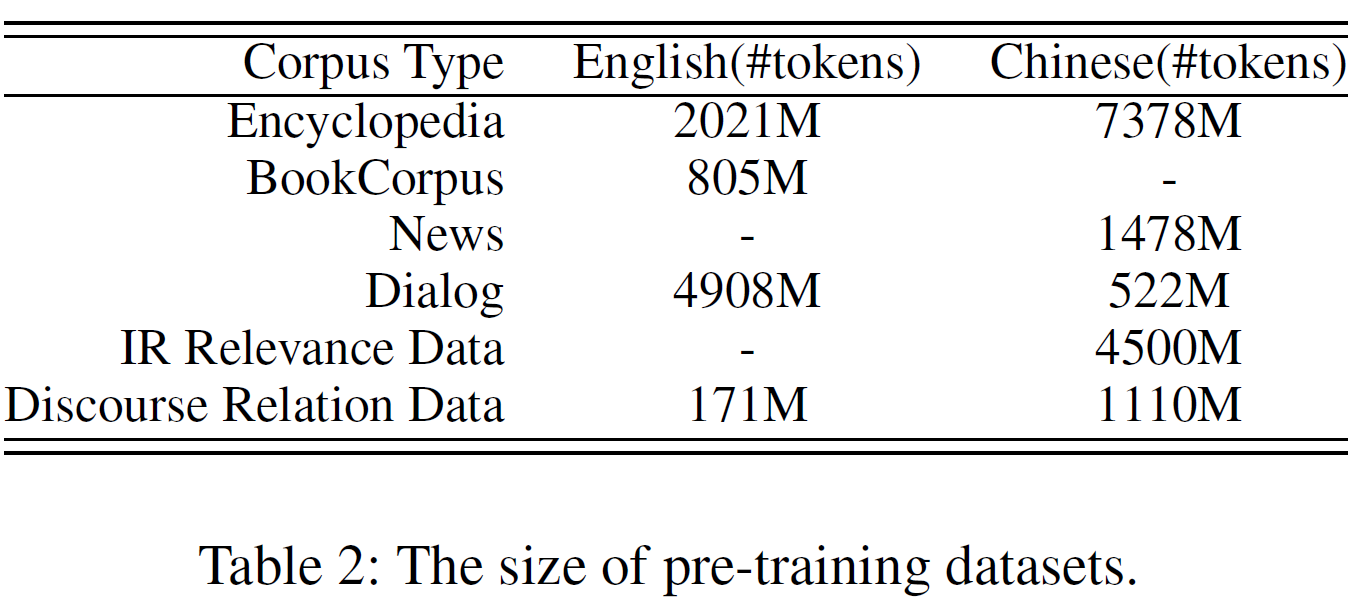
Pre-training Settings: BERT와 비교를 위해 같은 크기의 Transformer 모델을 만들었다(base: 12 layers, 12 self-attention heads, 768-dim hidden size, large: 24 layers, 16 self-attention heads, 1024-dim hidden size). XLNet의 모델 세팅은 BERT와 같다.

ERNIE 2.0은 base 모델에서 48개의 Nvidia v100 GPU, large 모델에서 64개의 Nvidia v100 GPU를 사용하였다. ERNIE는 Baidu에서 end-to-end 오픈소스 딥러닝 플랫폼으로 개발한 PaddlePaddle 위에서 구현되었다.
Hyperparameter 세팅은 $\beta_1 = 0.9, \beta_2 = 0.98$이고 batch size는 393216 token이다. Learnint rate는 영어에서 $lr=5e-5$, 중국어 모델에서 $lr=1.28e-4$이며 decay scheme noam(4000 step의 warmup 포함)을 따른다. float16 연산으로 학습을 가속화했고 각 사전학습 task는 수렴할 때까지 진행되었다.

Fine-tuning Tasks

English Task: GLEU benchmark를 사용하였다.

Chinese Tasks: 9개의 중국어 자연어처리 task에서 실험을 진행하였다(독해, 명명 객체 인식, 자연어추론, 의미적 유사성, 감정분석, 질의응답 등). 중국어 데이터셋은 다음 중에서 선택되었다.

• Machine Reading Comprehension (MRC): CMRC 2018 (Cui et al. 2018), DRCD (Shao et al. 2018), and DuReader (He et al. 2017).
• Named Entity Recognition (NER): MSRA-NER (Levow 2006).
• Natural Language Inference (NLI): XNLI (Conneau et al. 2018).
• Sentiment Analysis (SA): ChnSentiCorp.
• Semantic Similarity (SS): LCQMC (Liu et al. 2018), and BQ Corpus (Chen et al. 2018).
• Question Answering (QA): NLPCC-DBQA.

Implementation Details for Fine-tuning

영어 및 중국어 세팅(Epoch, Learning rate, Batch size)을 아래 표에 표시하였다.

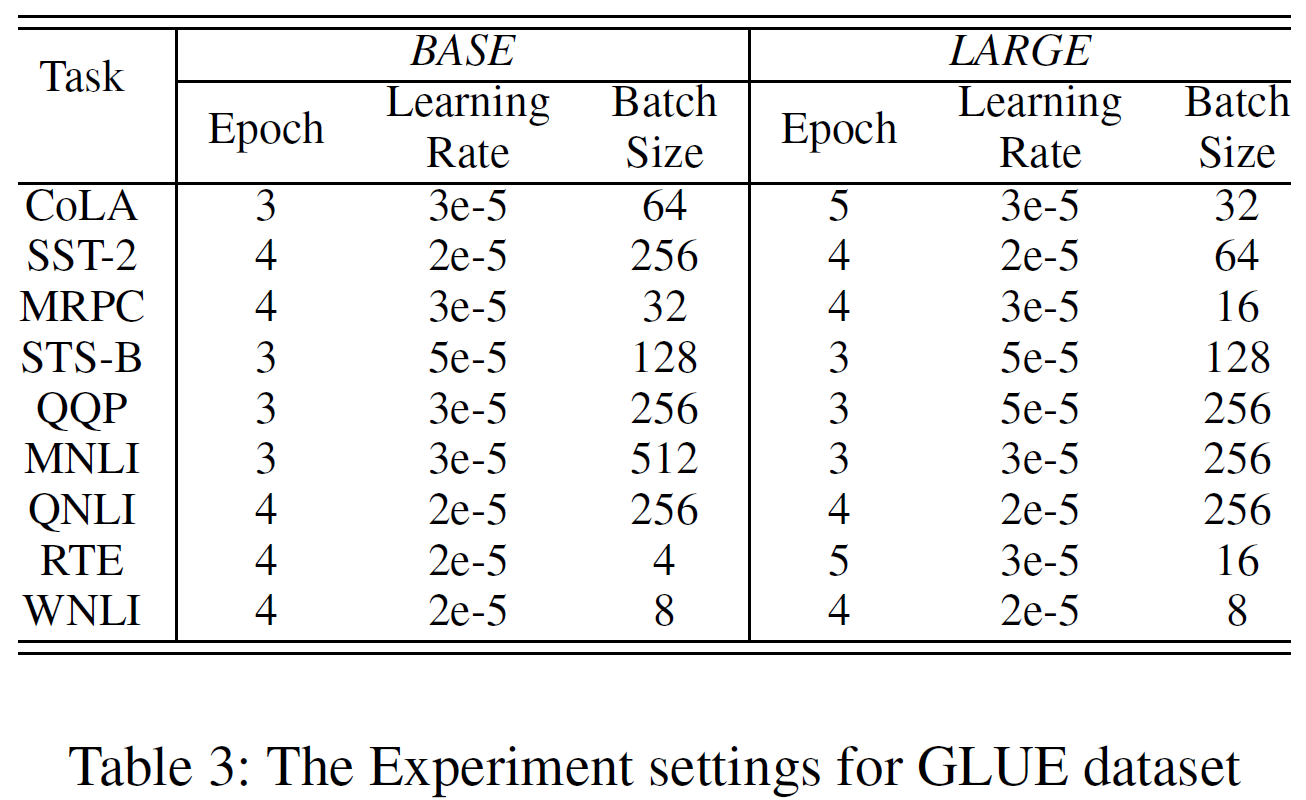
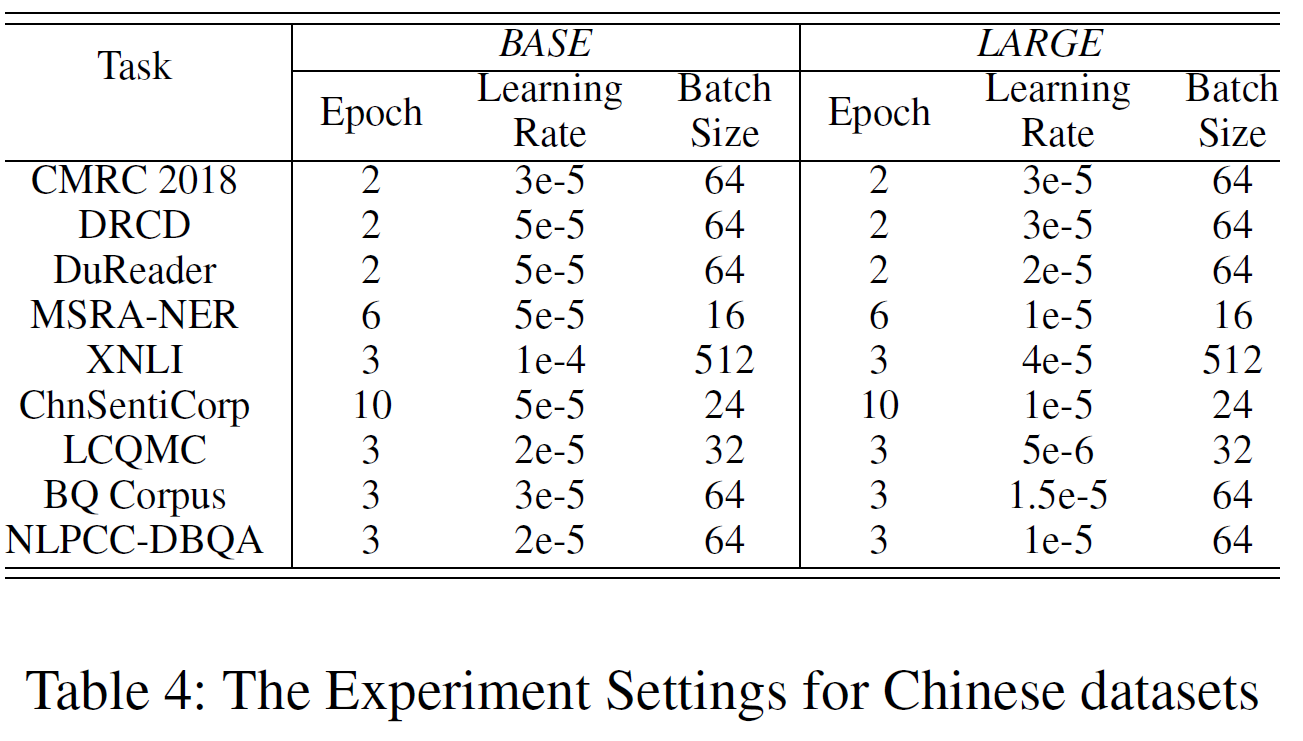
Experimental Results

Results on English Tasks: 각 방법의 base와 large 모델을 GLUE에서 평가하였다. XLNet의 dev set만 보고되어 있는 관계로 다른 방법도 dev set에서의 결과를 표시한다. BERT와 XLNet과 비교를 위해 단일 task와 단일 모델 ERNIE 2.0을 테스트하였다. GLUE에 대한 결과는 표 5와 같다.

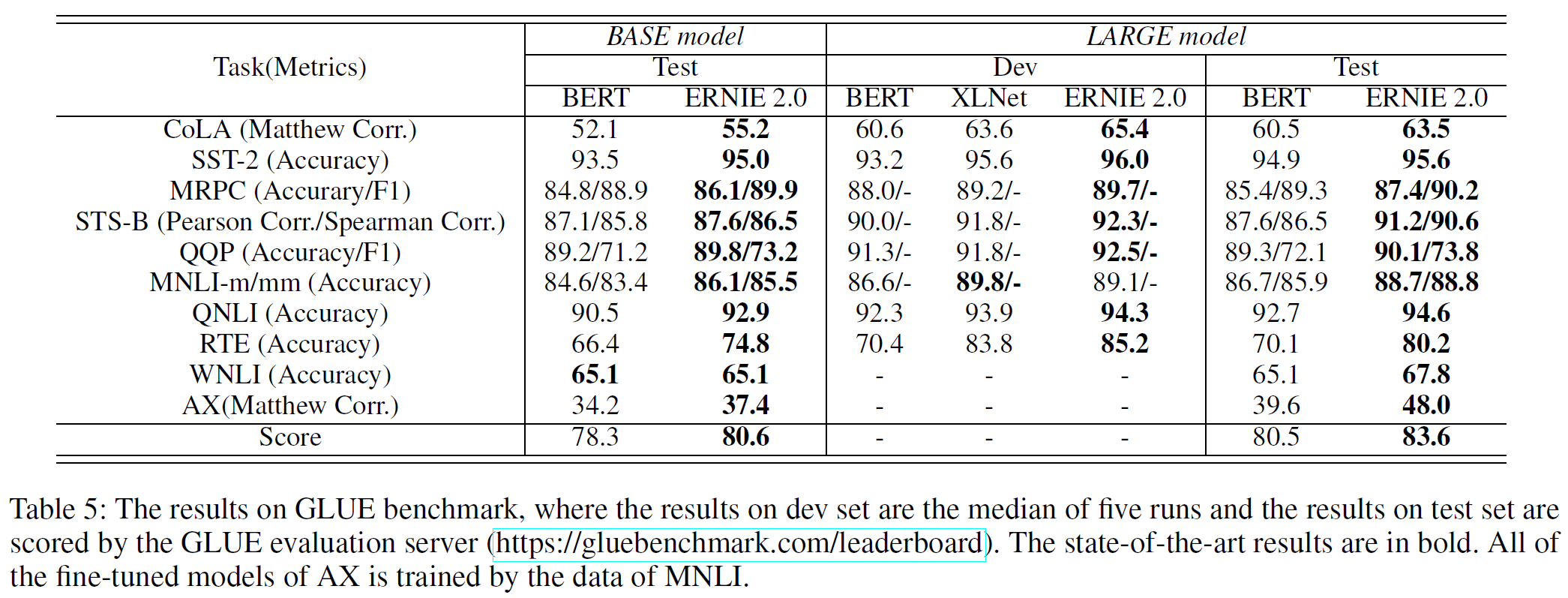
ERNIE 2.0 base 모델이 BERT base 모델을 모든 task에서 상회하며 80.6점을 얻었다. Large 모델의 경우 ERNIE 2.0이 BERT와 XLNet을 단 한 개의 task를 제외하고 모든 부분에서 상회하며 GLUE 점수는 83.6점으로 3.1% 향상시킨 것을 볼 수 있다.

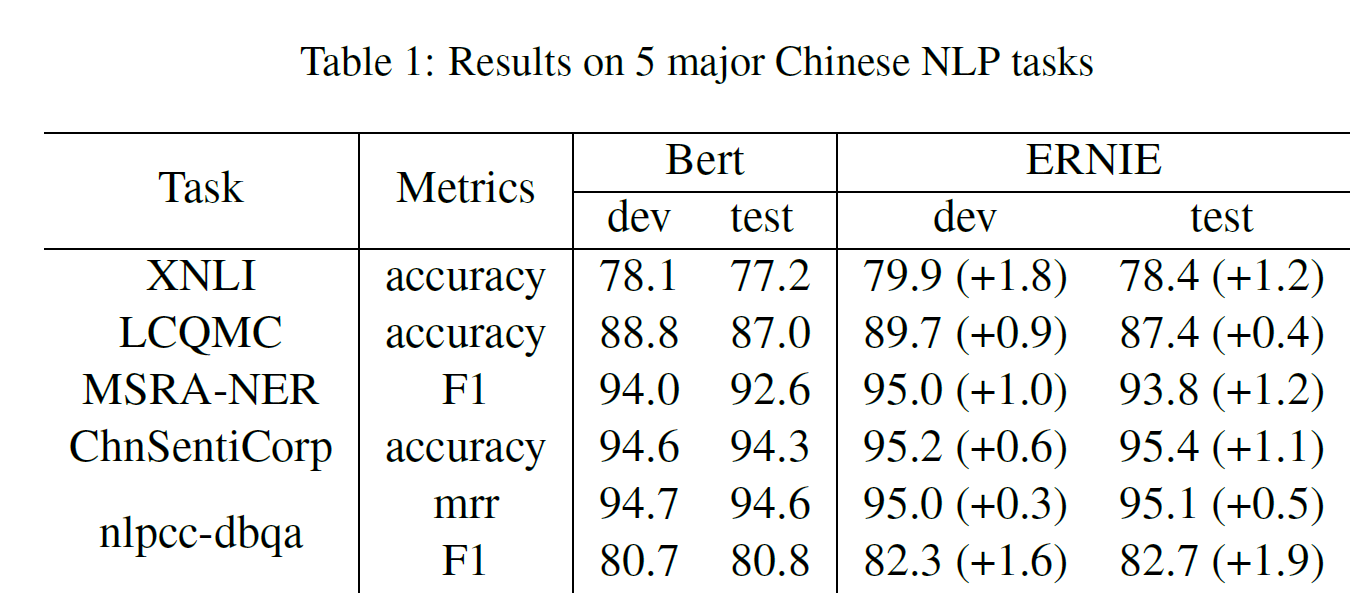
Results on Chinese Tasks: 표 6은 중국어 task에서 결과를 보여준다.

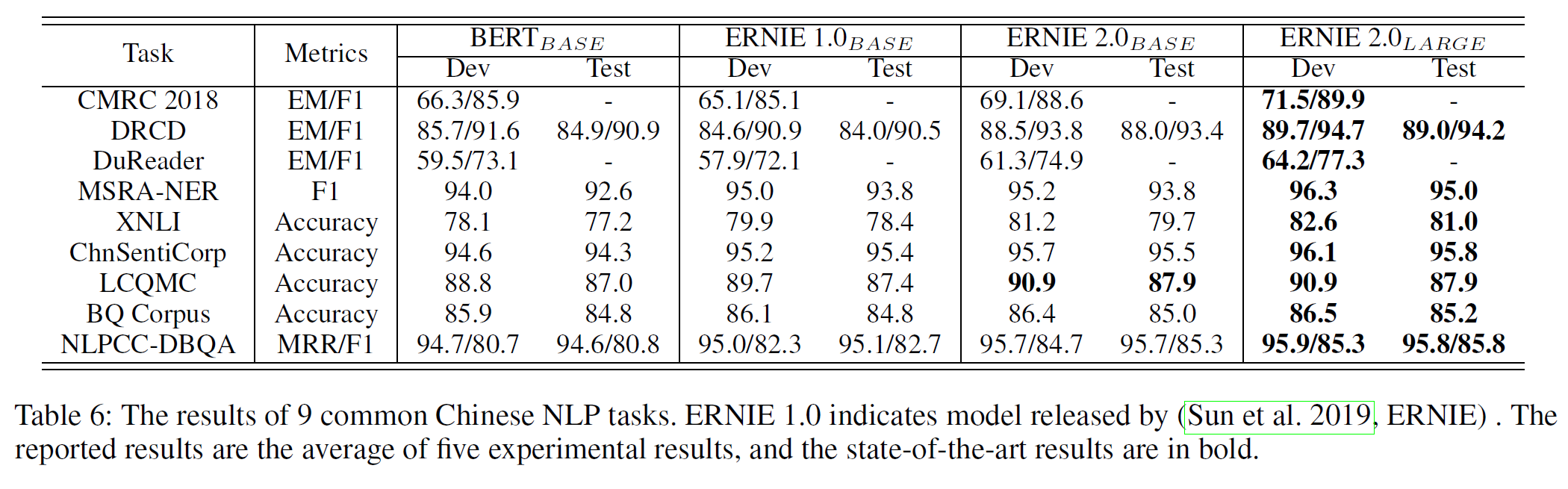
ERNIE 1.0이 BERT base를 5개의 task에서 상회함을 보여주지만 이상적이지는 않은 결과인데 사전학습의 차이로 보인다. 구체저으로 ERNIE 1.0 base의 경우 길이 128 이상의 instance를 포함하지 않으나 BERT base는 512까지 사용한다. ERNIE 2.0은 BERT base를 모든 task에서 압도하며 ERNIE 2.0 large 모델은 제시된 모든 중국어 task에서 SOTA 결과를 얻었다.

Comparison of Different Learning Methods

ERNIE 2.0 framework에 적용한 연속적 mult-task 학습 전략의 효과를 분석하기 위해 그림 2에서 나온 2가지 방법을 비교하였다. 아래 표 7에서 세부 사항을 볼 수 있다. 모든 방법에서 학습 반복횟수는 각 task에서 같다고 가정한다. 각 task는 50k회의 반복 학습을 하며 총 200k번의 학습을 한다. multi-task는 한 단계에서 모든 task를, 연속적 사전학습 방법은 한 번에 하나의 task를, 연속적 multi-task 학습 방법(본 논문에서 제시)는 각 단계마다 서로 다른 반복횟수를 적용하여 점진적으로 학습하는 것을 볼 수 있다.

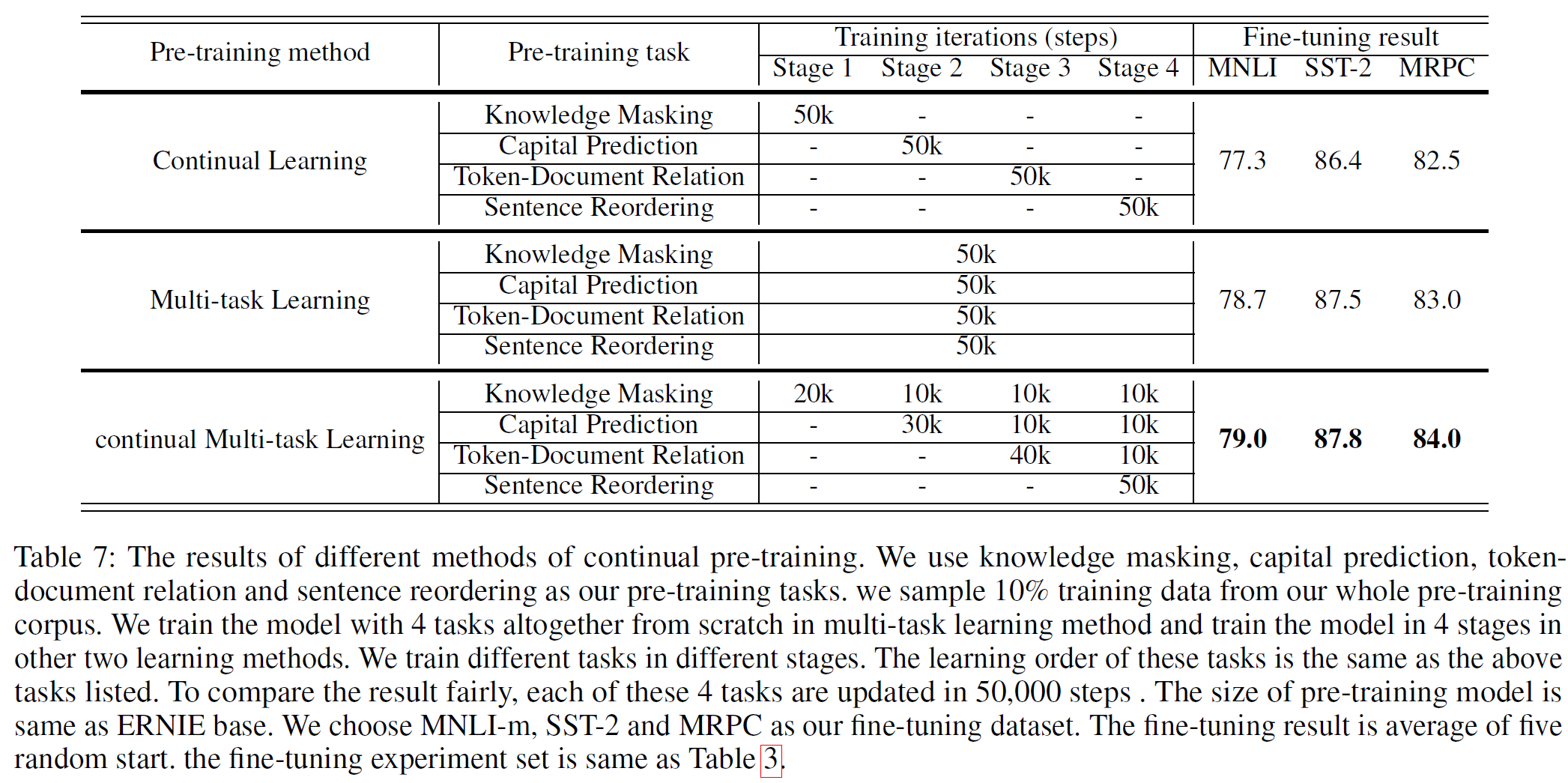
실험 결과에서 본 논문에서 제시된 방법이 효율을 희생하지 않으면서 가장 효과가 좋다는 것을 확인할 수 있다. 이는 본 논문에서 제시된 사전학습 방식이 새로운 task를 학습하는 데 있어 더 효율적이고 효과적임을 보여준다. 또한, 이 비교 결과는 연속적 학습 방법이 단순 multi-task 학습 방법을 능가한다는 것을 뜻하고 새로 제시된 방법은 이전 학습에서 얻은 지식을 잘 잊어버리지 않는다는 것을 의미한다.

결론(Conclusion)

본 논문에서 연속적 사전학습 framework인 ERNIE 2.0을 제안하였고 사전학습 task들은 점진적으로 추가되며 연속적 multi-task 학습 방법을 통해 학습된다. 이 framework에 기반하여 언어의 다양한 부분을 커버하는 여러 사전학습 task를 구성하였다. GLUE와 여러 중국어 task에서 좋은 결과를 보였으며 BERT와 XLNet을 상회하는 성과를 얻었다. 앞으로 모델의 성능을 더 발전시킬 수 있는 사전학습 task들을 소개하며 더 세련된 학습 방식을 연구할 계획이다.

참고문헌(References)

논문 참조!

본 글에서는 2018년에 발표된 Session-based Recommendation with Graph Neural Networks라는 논문에 대한 Review를 진행할 것이다. 단순히 논문을 읽어보는 것을 넘어서서, 실제 추천 시스템에서 활용하는 상황을 가정하고 설명을 진행해 볼 것이다.

보통의 세션 기반의 추천 알고리즘의 경우 Recurrent Neural Networks에 기반하여 설계된 경우가 많은데, SR-GNN의 경우 Recurrent Unit과 Graph Neural Network를 결합하여 독특한 형태의 방법론을 제시하고 있다.

세션 기반의 추천 시스템은 익명의 세션에 기반하여 User의 행동을 예측하는 데에 목적을 둔다. 그러나 과거의 여러 연구들을 보면, 세션에서 정확한 User Embedding 벡터를 얻기에는 부족하고 Item 간의 복잡한 transition을 무시하는 경향을 보이곤 했다.

이러한 문제를 해결하기 위해 본 논문에서는 SR-GNN이라는 기법을 제시한다. GNN을 통해 이전의 전통적인 Sequential한 방법들에서는 어려웠던, Item 간의 복잡한 transition을 포착하는 것이 본 방법론의 핵심이다.

Session-based Recommendation with Graph Neural Networks 리뷰

1. Introduction

RNN, NARM, STAMP 등의 여러 방법론이 세션 기반의 추천을 위해 도입되었지만 다음과 같은 한계점을 지닌다. 우선 하나의 세션 내에서 적절한 User 행동이 존재하지 않으면, User Representation을 추정하는데에 어려움을 겪는다는 것이다. 보통 이러한 방법들에서는 RNN의 Hidden Vector가 User Representation으로 취급되는데, 사실 세션은 그 수가 방대하고 충분한 정보가 주어지지 않는다면 세션과 User를 잇기 어렵기 때문에 (익명성) 이러한 방법으로는 각 세션 내에서 User Representation을 추정하기가 쉽지 않은 것이다.

그리고 이전의 연구들에서 분명 Item 간의 transition의 중요성에 대해 밝힌 바는 있으나, 맥락 속에서 발생하는 transition을 무시한 채 단 방향의 transition 만을 고려했다는 문제점을 지닌다.

위 문제점을 해결하기 위해 소개하는 SR-GNN은 Item 사이에서 풍부한 transition을 탐구하고 Item에 대한 정확한 잠재 벡터를 생성할 수 있는 알고리즘이다.

위 그림은 SR-GNN의 구조를 대략적으로 나타낸 것이다. $v_1, …, v_7$ 는 추천 대상인 Item 리스트를 의미한다. 모든 세션 Sequence를 directed session graph로 나타내면, 각 세션 Graph는 하나의 subgraph로 생각할 수 있다. 위 예시에서는 $v_2 \rightarrow v_5 \rightarrow v_6 \rightarrow v_7$ 로 이어지는 하나의 세션을 subgraph로 생각하면 된다.

이제 각 세션은 차례대로 하나씩 위 Workflow을 타고 흐르게 된다. 첫 번째 세션은 $s_1 = [v_1 \rightarrow v_2 \rightarrow v_3 \rightarrow v_4]$ 라고 해보자. 웹사이트나 어플 상의 로그 기록을 기반하여 세션을 구성한다고 하면 위 세션은 어떤 4개의 Item을 순차적으로 클릭한 데이터를 표현한 것이다. 이 세션 데이터는 Gated Graph Neural Network를 통과하여 각각의 Node 벡터를 얻게 된다.

그리고 나서 이를 활용하여 우리는 최종적으로 $\mathbf{s_g}, \mathbf{s_l}$ 이라는 2개의 벡터를 얻게 되는데, 전자는 Global한 선호를 반영하는 Global Session Vector를, 후자는 그 세션 내에서의 User의 현재의 관심을 나타내는, 즉 가장 최근에 클릭/반응한 Item을 나타내는 Local Session Vector를 의미한다.

최종적으로 본 모델은 각 세션에 대해 다음 클릭의 대상자가 될 Item을 예측한다.

2. Related Work

(중략)

3. The Proposed Method

Notations

Constructing Session Graphs
전체 Graph는 아래와 같이 정의할 수 있다.

[\mathcal{G} = ( \mathcal{V}, \mathcal{E} )]

모든 세션 Sequence $s$ 는 아래와 같은 Directed Graph로 정의할 수 있다.

[\mathcal{G}_s = ( \mathcal{V_s}, \mathcal{E}_s )]

이 세션 Graph에서 각 Item Node는 $v_{s, i} \in V$ 를 나타낸다. 각 Edge $(v_{s, i-1}, v_{s, i}) \in \mathcal{E_s}$ 는 세션 $s$ 에서 $v_{s, i-1}$ 를 클릭한 후에 $v_{s, i}$ 를 클릭했다는 의미이다.

똑같은 Item이 반복적으로 나올 수 있기 때문에 본 논문에서는 각 Edge에 대해 Normalized Weight을 적용하였다. 모델을 통과한 후, 각 Item $v$ 는 Gated GNN을 통과하여 아래와 같이 통합된 Embedding Space에 임베딩되어 Node 벡터로 표현된다.

[\mathbf{v} \in \mathbb{R^d}]

그리고 각 세션 $s$ 는 Graph에서의 Node 벡터들로 이루어진 $\mathbf{s}$ 라는 임베딩 벡터로 표현된다.

Learning Item Embeddings on Session Graphs
세션 Graph 내에서 이루어지는 Node 벡터의 학습 과정에 대해 알아보자. $t-1$ 시점의 Node 벡터를 활용하여 $t$ 시점의 Node 벡터를 얻게 되는 과정이라고 생각하면 된다. 먼저, 세션 $s$ 내의 $n$ 개의 Node가 주어졌다고 할 때 이들의 Node 임베딩 벡터를 아래와 같이 활용하게 된다.

[\mathbf{a}^t_{s, i} = \mathbf{A}_{s, i:} [\mathbf{v}_1^{t-1}, …, \mathbf{v}_n^{t-1}] \mathbf{H} + \mathbf{b}]

$n=4$ 인 세션을 예로 들어보자. 위와 같은 Subgraph가 있다고 할 때, $\mathbf{A_s}$ 는 위와 같이 표현된다.

이 때 아래 기호로 표기된 Block은

[\mathbf{A}_{s, i:} \in \mathbb{R}^{1 * 2n}]

다음과 같은 Connection Matrix의 일부이다.

[\mathbf{A}_{s} \in \mathbb{R}^{n * 2n}]

따라서 형광색으로 표시한 부분이 위 예시에서 $\mathbf{A}_{s, 2:}$ 가 될 것이다.

위 식을 통해 Gated Graph Neural Network를 활용하여 여러 Node 사이의 정보를 전파하는 과정을 수행하게 된다. 이 때 Connection Matrix $\mathbf{A_s}$ 를 통해 현재 관심 있는 Node, 예를 들어 $i=2$ 번째 Node $v_{s, 2}$ 와 관련있는 Row를 추출하여 이후 과정에 활용하게 된다. 즉 Edge가 존재하는 Neighbor들의 정보를 통합하여 $\mathbf{a}_{s, i}^t$ 라는 벡터로 나타내는 것이다. $\mathbf{H}$ 는 Weight를 조절하는 역할을 수행한다. (Parameter)

아래 두 식은 각각 Update Gate와 Reset Gate의 역할을 수행한다. 각각 어떤 정보를 보존하고 어떤 정보를 버릴 것인지를 결정하게 되는 것이다.

[\mathbf{z}{s, i}^t = \sigma (\mathbf{W}_z \mathbf{a}{s, i}^t + \mathbf{U}_r \mathbf{v}_i^{t-1})]

[\mathbf{r}{s, i}^t = \sigma (\mathbf{W}_r \mathbf{a}{s, i}^t + \mathbf{U}_r \mathbf{v}_i^{t-1})]

이후에는 Candidate State를 아래와 같이 얻게 된다. $t$ 시점, 즉 Current State의 정보를 얼마나 반영하고, $t-1$ 시점, 즉 Previous State의 정보를 얼마나 Reset하는지를 결정하여 Candidate State 값을 얻게 된다.

[\widetilde{\mathbf{v}i^t} = tanh( \mathbf{W}_o \mathbf{a}{s, i}^t + \mathbf{U}o (\mathbf{r}{s, i}^t \odot \mathbf{v}_i^{t-1}) )]

Final State는 아래와 같이 Previous Hidden State인 $\mathbf{v}_i^{t-1}$ 를 얼마나 Reset하고, Candidate State인 $\widetilde{\mathbf{v}_i^t}$ 를 얼마나 보존하는지를 통해 결정하게 된다.

[\mathbf{v}i^t = (1 - \mathbf{z}{s, i}^t) \odot \mathbf{v}i^{t-1} + \mathbf{z}{s, i}^t \odot \widetilde{\mathbf{v}_i^t}]

이렇게 세션 Graph들 내의 모든 Node에 대해 수렴할 때까지 Update를 진행하고 나면 Final Node Vectors를 얻게 된다.

[\mathbf{v}_1, \mathbf{v}_2, …, \mathbf{v}_m]

혼란을 방지하고자 다시 언급하면 $i$ 는 Node의 Index를 의미하며, $t$ 는 학습 Update 과정에서의 시점을 의미한다. 모든 업데이트가 끝나면 $t$ 는 필요 없는 기호가 된다.

각 벡터와 행렬의 길이, 차원 등을 정확히 파악하기 위해 아래와 같은 정리 식을 첨부하도록 하겠다.

Generating Session Embeddings
지금까지 과정을 통해 모든 세션 Graph를 Gated GNN에 투입하여 모든 Node에 대해 Embedding 벡터를 얻었다. 이제 이렇게 얻은 벡터 값에 기반하여 세션 Embedding을 얻는 방법에 대해 알아보자.

세션 Embedding을 $\mathbf{s} \in \mathbb{R}^d$ 라고 표기하겠다. 이제 이 벡터는 아래와 같이 2가지 벡터를 결합하여 구성할 것이다.

Local Session Embedding은 간단하다. 아래와 같이 가장 최근에 클릭한 Item $v_{s, n}$ 의 Embedding 값을 그대로 쓰면 된다.

[\mathbf{s}_l = \mathbf{v}_n]

해당 세션 Graph $\mathcal{G}_s$의 Global Session Embedding은 모든 Node 벡터를 통합하여 얻을 수 있다. 그런데 이들에 대한 중요도는 각각 다를 것이므로 Soft-attention Mechanism을 사용한다.

[\alpha_i = \mathbf{q}^T \sigma ( \mathbf{W}_1 \mathbf{v}_n + \mathbf{W}_2 \mathbf{v}_i + \mathbf{c} )]

[\mathbf{s}g = \Sigma{i=1}^n \alpha_i \mathbf{v}_i]

식을 보면 Attention Score를 계산할 때 필수적으로 마지막에 클릭한 Item의 Embedding 벡터 값이 고려되는 것을 확인할 수 있다.

이렇게 얻은 두 벡터와 Trainable Parameter Matrix를 활용하여 선형 변환 과정을 거치면 아래와 같이 Hybrid Embedding $\mathbf{s}_h$ 를 얻을 수 있다.

[\mathbf{s}_h = \mathbf{W}_3 [\mathbf{s}_l, \mathbf{s}_g]]

Making Recommendation and Model Training
추천 후보 Item $v_i \in V$ 가 있다고 할 때 이에 대한 Score $\hat{\mathbf{z}_i}$ 는 아래와 같이 계산된다.

[\hat{\mathbf{z}_i} = \mathbf{s}_h^T \mathbf{v}_i]

$m$ 개의 Item이 존재한다고 하면 이들 중 가장 높은 Score를 정해야 할 것이다. 이 때는 아래와 같이 Softmax 함수를 사용해준다.

[\hat{\mathbf{y}} = softmax(\hat{\mathbf{z}})]

다시 한 번 길이, 차원에 대해 정리한다.

Loss 함수는 아래와 같이 Cross-entropy 함수를 사용해주면 된다.

[\mathcal{L} (\hat{\mathbf{y}}) = - \Sigma_{i=1}^m \mathbf{y}_i log (\hat{\mathbf{y}}_i) + (1-\mathbf{y}_i) log (1-\hat{\mathbf{y}}_i)]

그리고 이 SR-GNN을 학습하기 위해서는 Back-Propagation Through Time 알고리즘이 사용된다. 일반적으로 세션의 길이는 굉장히 짧기 때문에 과적합을 막기 위해서는 비교적 작은 수의 학습 Epoch이 적용되어야 할 것이다.

4. Experiments and Analysis

본 섹션의 경우 상세 내용에 대해서는 논문 원본을 참조하길 바란다. 다만 세팅과 관련하여 주요 내용만 메모하도록 하겠다.

세션 $s$ 가 아래와 같이 주어져 있다고 하면,

[s = [v_{s, 1}, v_{s, 2}, …, v_{s, n}]]

학습을 위해서는 아래와 같이 Sequence를 구성할 수 있다.

$([v_{s, 1}], , v_{s, 2})$, $([v_{s, 1}, v_{s, 2}], v_{s, 3})$ …

Validation Set의 비율은 10%로 설정하였으며 모든 파라미터는 평균0, 표준편차0.1의 정규분포로 초기화하였고, Adam Optimizer가 사용되었다. 최초의 Learning Rate은 0.001이나 3 Epoch마다 0.1의 Decay가 적용되었다. 100의 Batch Size와 $10^{-1}$ 의 L2 페널티가 적용되었다.

5. Conclusions

세션 기반의 추천 시스템은 User의 분명한 선호와 이전의 기록을 얻기 어려울 때 굉장히 유용하다. 본 논문은 Graph 모델을 통해 세션 Sequence를 표현하는 새로운 구조를 제안하였다. SR-GNN을 통해 Item 사이의 복잡한 구조와 transition을 고려할 수 있으며 또한 User의 다음 행동을 예측하기 위해 Long-term 선호와 최근 선호까지 복합적으로 반영하는 전략을 구사할 수 있다.

References

1) 논문 원본

이 글에서는 ERNIE 타이틀을 달고 나온 Tsinghua University에서 발표한 ERNIE: Enhanced Language Representation with Informative Entities 논문을 살펴본다.

중요한 부분만 적을 예정이므로 전체가 궁금하면 원 논문을 찾아 읽어보면 된다.

ERNIE: Enhanced Language Representation with Informative Entities

논문 링크: ERNIE: Enhanced Representation through Knowledge Integration

Official Code: Github

초록(Abstract)

대규모 말뭉치에서 사전학습하는 BERT같은 자연어표현 모델은 텍스트로부터 충분한 의미적 패턴을 잘 잡아내며 다양한 NLP 문제에서 미세조정을 통해 일관되게 성능이 향상되는 모습을 보인다.
그러나, 현존하는 자연어 모델은 더 나은 언어 이해를 위한 풍부한 구조적 지식을 제공할 수 있는 지식 그래프(Knowledge Graphs, KGs)를 거의 고려하지 않는다. 우리는 KGs 내의 유익한 entity들이 외부 지식을 통해 언어표현을 향상시킬 수 있다고 주장한다. 본 논문에서, 대규모 텍스트 말뭉치와 KGs를 사용하여 향상된 언어표현 모델 ERNIE를 학습하며 이는 어휘적, 의미적, 지식 정보를 동시에 학습할 수 있다.
실험 결과는 ERNIE가 다양한 지식기반 문제에서 상당한 발전을 이루었고 또한 다를 NLP 문제에서도 SOTA 모델 BERT에 필적할 만하다.

1. 서론(Introduction)

Feature 기반이나, 미세조정 등을 사용하는 언어표현 사전학습 모델들은 텍스트로부터 풍부한 언어표현을 얻을 수 있고 이는 많은 자연어처리 문제에서 상당한 효과를 거두었다. 최근 제안되었던 BERT와 그 응용 모델들은 named entity, 질답, 자연어추론, 텍스트 분류 등 많은 자연어 문제에서 뛰어난 성과를 보여주었다.

그러나 이러한 언어표현 사전학습 모델은 언어이해를 위해 필요한 연관 지식을 무시한다. 아래 그림에서 보듯이, Blowin’ in the Wind and Chronicles: Volume One are song and book라는 지식 없이 Bob Dylan의 직업 songwriter and writer를 식별하는 것은 어려운 일이다. 더욱이, 관계 분류 문제에서 composer과 author와 같은 fine-grained 관계를 찾는 것은 거의 불가능하다. UNK wrote UNK in UNK와 같은 문장은 언어표현 사전학습 모델에게 구문으로 모호하다. 따라서, 풍부한 지식 정보를 활용하는 것이 언어이해에 도움을 주고 다양한 지식기반 문제에서 이득을 가져다줄 것이다.

언어표현 모델에 외부 지식을 잘 포함시키려면 다음 두 가지를 해결해야 한다.

1. 구조화된 지식 Encoding
   • 주어진 텍스트와 관련하여 효율적으로 추출하고 언어표현 모델을 위해 KGs에서 유용한 정보를 찾는 것은 중요한 문제이다.
2. 다차원적 정보 융합
   • 언어표현을 위한 사전학습 절차는 지식표현과는 상당히 다른데, 2개의 독립적인 벡터공간을 다루기 때문이다.

어떻게 특별한 사전학습 목적함수를 어휘적, 구문, 지식정보와 융합하는 것은 또 다른 도전적인 과제이다.

위와 같은 문제를 극복하기 위해 ERNIE(Enhanced Language RepresentatioN with Informative Entities)를 제안한다. 대규모 말뭉치와 KGs를 모두 사용한다.

1. 지식 정보를 추출하고 인코딩하기 위해, 텍스트에서 named entity(명명 객체)를 구분하고 KGs 안의 해당하는 entity를 언급하는 것과 묶는다. KGs의 그래프 기반 사실들을 직접 사용하기보다는 TransE를 사용하여 그래프 구조를 인코딩하고 지식 embedding을 ERNIE의 입력으로 사용한다. 텍스트와 KGs 사이의 alignment에 기반하여 entity 표현을 통합하고 의미 모듈로 보낸다.
2. BERT와 비슷하게 maksed 언어모델을 적용하여 사전학습 목적함수로 다음 문장 예측을 사용한다. 텍스트와 지식 feature의 융합을 위해 named entity alignment의 일부를 임의로 masking하고 alignment를 완성하도록 모델을 학습시킨다. 오직 지역적 문맥만을 활용하는 기존의 목적함수와는 다르게 본 모델에서는 token과 entity를 모두 예측하도록 문맥과 지식 정보를 모두 사용한다.

실험은 지식기반 자연어처리 문제, entity typing과 관계분류(relation classification)에 대해 진행하였다. 결과는 ERNIE가 어휘적, 구문, 의미정보를 최대한 사용하여 SOTA인 BERT를 압도하는 것을 보여주었다. 또한 다른 NLP 문제에도 실험하여 충분히 괜찮은 결과를 얻었다.

2. 관련 연구(Related Work)

단어를 분산표현(distributed representations)으로 변환하는 feature 기반 접근법이 2008~2018년까지 있었다. 텍스트 말뭉치를 갖고 사전학습 목적함수를 통해 학습하였으나 이전에는 단어의 다의성(polysemy)으로 인해 부정확했다. 2018년에는 문맥을 고려하여 이를 어느 정도 해결한 ELMo가 발표되었다.

사전학습에 더해 미세조정을 수행하는 방법으로 BERT, GPT2 등이 제안되어 다양한 자연어처리 문제에서 뛰어난 성과를 보였다.

이러한 feature 기반 및 미세조정 언어표현 모델은 상당한 성과를 보여주었으나 지식 정보를 활용하지 않는 단점이 있다. 외부 지식정보를 주입하는 방식으로 독해, 기계번역, 자연어추론 등에서 많은 논문들이 발표되었다. 그리고 여기서 우리는 외부 지식정보를 사용하는 것이 기존의 사전학습 모델에 도움이 될 것을 주장한다. 본 논문에서는 말뭉치와 KGs를 모두 활용, BERT에 기반하여 향상된 언어표현을 학습한다.

3. 방법론(Methodology)

3.1절은 표기법, 3.2절은 전체 구조, 3.4절은 사전학습 task, 3.5절은 미세조정 세부를 다룬다.

3.1. Notations

$n$은 token sequence의 길이, $m$은 entity sequence의 길이라 할 때 token sequence와 entity sequence는 다음과 같이 나타낸다. 모든 token이 KGs의 entity와 align되는 것은 아니므로 $n \ne m$일 수 있다.

[\lbrace w_1, …, w_n\rbrace , \lbrace e_1, …, e_m\rbrace]

모든 token을 포함하는 사전을 $\mathcal{V}$, KGs의 모든 entity를 포함하는 entity list를 $\mathcal{E}$라 한다. 어떤 token $w \in \mathcal{V}$가 해당하는 entity $e \in \mathcal{E}$를 가질 때, alignment는 $f(w) = e$로 정의한다. 그림 2에서 보듯이 entity는 named entity phrase에서 첫 번째 token으로 정한다.

3.2. Model Architecture

2개의 모듈을 쌓아 만들었다.

1. 아래쪽에 있는 textual encoder(T-Encoder)는 주어진 token에서 기본적인 어휘적, 문맥적 정보를 얻는다.
2. 위쪽의 knowledgeable encoder(K-Encoder)는 token에서 유래한 추가적인 지식 정보와 아래 layer의 textual 정보를 통합한다. 즉 token과 entity라는 다차원적 정보를 통합된 feature 공간에 표현할 수 있게 된다.

T-Encoder layer의 수를 $N$, K-Encoder layer의 수를 $M$이라 한다.

구체적으로, token sequence와 entity sequence가 주어지면, textual encoder는 먼저 각 token에 대해 token/segment/positional embedding을 합하고 어휘적, 구문 feature를 계산한다.

[\lbrace w_1, …, w_n\rbrace = \text{T-Encoder}(\lbrace w_1, …, w_n\rbrace)]

T-Encoder($\cdot$)은 multi-layer 양방향 Transformer encoder이다. T-Encoder($\cdot$)은 BERT 구현체와 동일하다. 자세한 구조는 BERT와 Transformer 참조.

feature를 계산하면 ERNIE는 knowledgeable encoder K-Encoder를 사용하여 언어표현에 지식정보를 주입한다. 구체적으로, 지식 임베딩 모델 TransE로 사전학습된 entity embedding을 표현하고, $w$와 $e$ 모두를 K-Encoder에 입력으로 주어 다차원적 정보를 융합하고 최종 embedding 출력을 뽑아낸다.

[\lbrace w_1^o, …, w_n^o\rbrace, \lbrace e_1^o, …, e_n^o\rbrace = \text{K-Encoder}(\lbrace w_1, …, w_n\rbrace, \lbrace e_1, …, e_m\rbrace)]

$ \lbrace w_1^o, …, w_n^o\rbrace, \lbrace e_1^o, …, e_n^o\rbrace $는 특정 task를 위한 feature로 사용된다. K-Encoder의 세부적인 내용은 아래 절 참고.

3.3. Knowledgeable Encoder

K-Encoder는 aggregator를 쌓아 만든 구조로 token과 entity 모두를 인코딩하여 그 다차원적 feature를 융합하는 것을 목표로 한다. $i$-th aggregator에서, $(i-1)$-th aggregator에서 올라온 입력 token embedding $\lbrace w_1^{(i-1)}, …, w_n^{(i-1)}\rbrace$와 entity embedding $\lbrace e_1^{(i-1)}, …, e_m^{(i-1)}\rbrace$을 2개의 multi-head self-attentions(MH-ATTs)에 각각 넣는다.

[\lbrace \tilde{w}_1^{(i)}, …, \tilde{w}_n^{(i)}\rbrace = \text{MH-ATT}(\lbrace w_1^{(i-1)}, …, w_n^{(i-1)}\rbrace)]

[\lbrace \tilde{e}_1^{(i)}, …, \tilde{e}_n^{(i)}\rbrace = \text{MH-ATT}(\lbrace e_1^{(i-1)}, …, e_n^{(i-1)}\rbrace)]

그리고, $i$-th aggregator는 token과 entity sequence의 상호 통합을 위한 정보융합 layer를 사용, 각 token과 entity에 대한 출력 embedding을 계산한다. Token $w_j$와 상응하는 entity $e_k = f(w_j)$에 대해, 정보융합 과정은 아래와 같다.

[h_j = \sigma(\tilde{W}_t^{(i)}\tilde{w}_j^{(i)} + \tilde{W}_e^{(i)}\tilde{e}_k^{(i)} + \tilde{b}^{(i)})]

[w_j^{(i)} = \sigma(W_t^{(i)}h_j + b_t^{(i)}) \qquad \qquad \qquad]

[e_k^{(i)} = \sigma(W_e^{(i)}h_j + b_e^{(i)}) \qquad \qquad \qquad]

$h_j$는 token과 entity의 정보를 통합하는 inner hidden state이다. $\sigma(\cdot)$은 비선형 활성함수로 GELU를 사용했다.

상응하는 entity가 없는 token의 경우, 정보융합 layer는 통합 없이 embedding을 계산한다.

[h_j = \sigma(\tilde{W}_t^{(i)}\tilde{w}_j^{(i)} + \tilde{b}^{(i)})]

[w_j^{(i)} = \sigma(W_t^{(i)}h_j + b_t^{(i)})]

단순히, $i$-th aggregator 연산은 아래와 같이 쓸 수 있다.

[\lbrace w_1^{(i)}, …, w_n^{(i)}\rbrace, \lbrace e_1^{(i)}, …, e_m^{(i)}\rbrace = \text{Aggregator}(\lbrace w_1^{(i-1)}, …, w_n^{(i-1)}\rbrace, \lbrace e_1^{(i-1)}, …, e_m^{(i-1)}\rbrace)]

가장 위의 aggregator에서 나온 출력은 K-Encoder의 최종 output embedding으로 사용된다.

3.4. Pre-training for Injecting Knowledge

언어표현에 지식정보를 집어넣기 위해서 ERNIE를 위한 새 사전학습 task를 만들었다. 일부 token-entity alignments를 임의로 masking하고 시스템은 aligned token에 대한 모든 상응하는 entity를 찾는 것을 목표로 한다. 이는 auto-encoder를 denoising하는 것과 비슷하기에 이를 denoising entity auto-encoder(dEA)라 한다.

$\mathcal{E}$의 크기는 softmax layer에 비해 너무 크기 때문에, 시스템은 전체 KGs에 있는 것이 아닌 주어진 entity sequence만에 대해서 대응되는 entity를 찾으면 된다. token sequence $\lbrace w_1, …, w_n \rbrace$과 entity sequence $\lbrace e_1, …, e_n \rbrace$가 주어지면, token $w_i$에 대한 aligned entity 분포는 다음과 같이 나타낸다.

[p(e_j \vert w_i) = \frac{\text{exp(linear}(w_i^o) \cdot e_j)}{\Sigma_{k=1}^m \text{exp(linear}(w_i^o)\cdot e_k)}]

위의 식은 dEA를 위한 cross-entropy loss 함수로 사용될 것이다.

token-entity alignment에서 오류가 있을 수 있기 때문에, dEA를 위해 다음과 같은 연산을 수행하였다.

1. 5%의 경우에는 주어진 token-entity alignment에 대해 entity를 다른 임의의 entity로 교체하고 모델이 이를 바로잡도록 목표로 하였다.
2. 15%의 경우에는 token-entity alignment를 masking하여 모델이 entity alignment 시스템이 존재하는 모든 alignment를 추출하지 않도록 학습하는 것을 목표로 한다.
3. 나머지(80%)는 token alignment를 바꾸지 않고 두어 더 나은 언어이해를 위해 entity 정보를 token 정보와 통합하는 것을 목표로 한다.

BERT와 비슷하게, ERNIE는 MLM(Masked Language Model)과 NSP(Next Sentence Prediction)을 사전학습 task로 하여 어휘적, 구문 정보를 얻을 수 있게 한다.
사전학습 task의 전체 손실함수는 dEA, MLM, NSP loss를 전부 합한 것이다.

3.5. Fine-tuning for Specific Tasks

BERT와 비슷한 미세조정 과정을 거친다. [CLS]를 특별 token으로 문장의 처음을 가리키는 것으로 사용한다.

관계분류(relation classification) 문제에서, 시스템은 주어진 entity pair가 문맥에 기반하여 어떤 관계를 갖는지 판별해야 한다. 입력 token sequence에 2개의 mark token을 추가하여 entity mention을 강조한다. 이러한 추가적인 mark token은 전통적인 관계분류 문제에서 position embedding과 비슷한 역할을 한다. 그리고 [CLS] token을 분류를 위해 사용한다. [HD]와 [TL]은 각각 head entity와 tail entity를 나타낸다.

Entity typing을 위한 미세조정 과정은 관계분류에서 사용한 방법을 간소화한 것과 같다. 전체 문맥 embedding과 entity mention embedding을 쓰는 대신 Mention mark token [ENT]는 ERNIE가 문맥정보와 entity mention 정보를 잘 결합할 수 있게 해 준다.

4. Experiments

4.1. Pre-training Dataset

사전학습 과정은 이전의 다른 사전학습 모델과 비슷하다. Transformer 블록을 초기화할 때는 BERT의 것을 가져다 썼다. 영문 위키를 말뭉치와 align 텍스트로 사용하였다. 말뭉치를 사전학습을 위한 형식화된 데이터로 변환한 후에는, 주석 포함된(annotated) 입력은 4500M 보조단어와 140M개의 entity를 포함하며, 3개 이하의 entity를 가진 문장은 제외하였다.

ERNIE를 사전학습하기 전에는 Wikidata에서 학습된 knowledge embedding을 적용하였다. Wikidata는 5M개의 entity와 24M개의 fact triplet을 포함한다.

4.2. Parameter Settings and Training Details

token / entity embedding의 hidden dimension을 $H_w=768, H_e=100$이고, self-attention head의 수는 $A_w=12, A_e=4$, $N=6, M=6$이다. 전체 parameter의 개수는 114M개이다. 이는 BERT-base와 비슷한 수치(110M)로 ERNIE의 knowledgeable module이 언어 module보다 더 작으며 실행시간에 더 적은 영향을 미친다.
학습을 가속하기 위해 최대 sequence 길이를 512에서 256으로 조정하고(self-attention의 학습 시간은 길이의 제곱에 비례) token의 수를 유지하기 위해 batch size는 256에서 두 배로 늘렸다.

4.3. Entity Typing

entity mention과 그 문맥이 주어질 때, entity typing은 시스템이 entity mention과 해당하는 의미 종류를 레이블링하도록 요구한다. 이 task에서 성능 측정은 FIGER와 Open Entity에 ERNIE를 미세조정하여 수행한다. FIGER의 학습 데이터셋은 distant supervision으로 레이블링되어 있으며 테스트셋은 사람에 의해 annotate되어 있다. Open-Entity는 완전히 사람에 의해 만들어진 데이터셋이다.

ERNIE를 다른 baseline 모델과 비교하였다. 아래는 데이터셋 통계와 실험 결과를 나타낸 것이다.

NFGEC

NFGEC는 hybrid 모델로 entity mention, 문맥, 수동으로 만든 추가 feature를 입력으로 하는 모델로 FIGER에서 SOTA이다. 단 본 논문에서는 수동 생성 feature는 쓰지 않았다.

UFET

UFET는 Open Entity 데이터셋에서 제안된 것으로 2개의 Bi-LSTM을 분리하여 사용하는 NFGEC와는 다르게 하나의 Bi-LSTM을 문맥 표현을 위해 사용한다.
또한 추가적으로 BERT를 비교하였다.

전체 실험 결과를 요약하면, ERNIE는 KGs에서 얻은 정보를 잘 주입하는 것으로 FIGER에서 noisy label 문제를 효과적으로 줄일 수 있다. 또한 Open Entity에서는 다른 baseline 모델을 능가한다.

4.4. Relation Classification

문장에서 두 entity의 관계를 판별하는 문제로 knowledge-driven 자연어처리 task에서 중요한 문제이다. 성능 측정을 위해서 FewRel과 TACRED를 사용하였으며, 비교 모델로 CNN, PA-LSTM, C-GCN을 사용하였다.

CNN

textCNN을 사용하는 모델로 position embedding이 사용되었다.

PA-LSTM

Position-Aware LSTM을 사용한 네트워크로 최종 문장표현을 위한 sequence의 각 단어에 대한 상대적 기여도를 평가한다.

C-GCN

Graph Convolution 연산을 사용한 모델로 의존성 parsing 문제를 줄이고 단어 순서를 인코딩하기 위해 Contextualized GCN(C-GCN)을 사용한 것으로 Bi-LSTM을 사용한다.
또한 BERT도 비교하였다.

Relation Classification 비교 실험 결과는 아래에서 볼 수 있다.

전체적으로, 추가 지식은 적은 데이터로도 모델 학습이 가능하게 하며, 이는 많은 데이터를 모으기가 어려운 대부분의 자연어처리 문제에서 상당히 중요한 결과이다.

4.5. GLUE

자연어처리에서 다양한 task에 대해 평가를 할 수 있는 GLUE benchmark에서 실험한 결과를 아래에 나타내었다.

BERT-large와 비교하여 비등하거나 조금 더 나은 결과를 보이는 것을 알 수 있다. 이를 통해 ERNIE는 다양한 정보융합 이후에도 textual 정보를 잃어버리지 않는다는 것을 알 수 있다.

4.6. Ablation Study

추가 정보 entity와 dEA의 효과를 알아보기 위해 entity와 dEA가 없는 버전의 모델을 갖고 실험하였다.

해당 모듈이 없을 때는 BERT와 비교하여 P, R, F1 score가 비슷하지만, 모듈을 추가한 최종 버전은 결과가 제일 좋음을 알 수 있다. 따라서 entity 정보와 dEA가 추가 지식을 잘 활용하여 모델의 성능에 도움을 준다는 것을 확인할 수 있다.

결론(Conclusion)

본 논문에서, ERNIE라는 정보통합 모델을 제안하였고 knowledgeable aggregator와 사전학습 task dEA를 제안하였다. 실험 결과를 통해 ERNIE는 추가 지식을 잘 활용하여 다양한 자연어처리 문제에서 성능 향상에 도움을 준다는 것을 확인하였고 데이터가 적은 상황에서도 유용함을 알 수 있었다.

추가 연구로,

1. ELMo와 같은 feature 기반 사전학습 모델에 지식을 주입하는 것
2. Wikidata와 같은 지식 데이터베이스와는 다른 형태인 ConceptNet과 같은 언어표현 모델에 다양한 구조화된 지식을 넣는 것
3. 더 큰 사전학습 데이터를 위한 실세계 말뭉치들을 annotate하는 것

을 생각해 볼 수 있다. 이는 더 범용적이고 효과적인 언어이해에 도움을 줄 수 있는 방향이 될 수 있을 것이다.

참고문헌(References)

논문 참조!

이 글에서는 Pytorch Docker를 생성하고 실행하는 방법을 정리한다.

Ctrl + F로 원하는 명령어를 검색하면 좋다.

기본 설명

여러 개의 Python 프로젝트에 참여하다 보면 각 프로젝트에서 사용하는 Python과 라이브러리들의 버전이 다른 경우가 대부분이다. 그래서 많은 경우 가상환경(python venv 또는 conda 등)을 사용하여 각 프로젝트의 환경을 분리하고는 하는데, Python을 여러 버전을 설치하기 곤란한 경우나 환경을 완전히 분리하고 싶은 경우에는 Docker(도커)를 사용할 수 있다.

Docker는 간단히 Container 기반의 Open-Source 가상화 플랫폼 정도로 정의할 수 있다. Container는 외부와 격리된 공간(파일 통신이 가능하긴 하지만, 일단 넘어가자)이며 내부에서 프로세스를 수행할 수 있다.

Docker를 사용하는 것은 마치 윈도우에서 가상머신을 돌리는 것과 비슷하다. 사실상 완전히 분리된 환경으로 동작하며, 한 환경에 설치된 라이브러리나 프로그램이 다른 환경에 아무런 영향을 미치지 못한다. 두 환경 간의 통신은 지정된 명렁어를 통해서만 가능하다.
참고: 엄밀히 말해서 가상머신과는 다르다. 가상머신은 추가적인 OS를 설치하여 가상화하는 방법인데, 이러한 방식은 Docker에 비해 추가적인 비용이 더 들기 때문에 실제 프로젝트 환경에서 쓰기에는 부적절하다.

Docker의 기본 사용법은 다음과 같다.

1. 필요한 세팅이 되어 있는 Docker Image를 인터넷에서 다운로드한다. 예: Pytorch Docker Image List
2. 다운받은 Docker Image로 새 Container를 생성한다. (같은 이미지로 여러 Container를 생성할 수 있다.)
3. 생성한 Container를 구동시키고(띄우고) 접속한다.
4. 필요한 Python 라이브러리를 마저 설치하고 사용 가능!

즉, 이미지 다운 → Container 생성 → 사용 순서를 따른다. 참 쉽죠?

설치 및 다운로드

Docker 설치

최신 Ubuntu라면 기본으로 설치되어 있는 경우가 많은 것 같긴 한데… 아니더라도 걱정할 필요는 없다.

curl -fsSL https://get.docker.com/ | sudo sh

password를 입력하고 기다리면 설치가 완료될 것이다.

Ubuntu가 아니라면 Windows나 Mac을 참고해보자.

최소 19.03 이상의 버전으로 설치하면 된다.

TroubleShooting

이 부분은 위의 설치가 안 되는 환경에서 설치방법을 다룬다.
이전 버전의 docker가 존재해서 문제가 되는 경우가 있는데, 이것들을 삭제하고 재설치하는 방법을 알아본다.

참고로 이전 버전의 docker는 docker, docker.io, docker-engine, 최신 버전은 docker-ce라고 한다.

먼저 삭제를 진행하자.

sudo apt-get remove docker docker-engine docker.io containerd runc

다음 코드를 터미널에 순차적으로 입력하자.

sudo apt-get update
sudo apt-get install apt-transport-https ca-certificates curl gnupg-agent software-properties-common

sudo apt-get update
# Docker official GPG key 추가
curl -fsSL https://download.docker.com/linux/ubuntu/gpg | sudo apt-key add -
# 결과: OK

sudo apt-key fingerprint 0EBFCD88

# 결과
pub   4096R/0EBFCD88 2017-02-22
      Key fingerprint = 9DC8 5822 9FC7 DD38 854A  E2D8 8D81 803C 0EBF CD88
uid                  Docker Release (CE deb) <docker@docker.com>
sub   4096R/F273FCD8 2017-02-22

docker repository를 추가하자.

sudo add-apt-repository "deb [arch=amd64] https://download.docker.com/linux/ubuntu $(lsb_release -cs) stable"

ModuleNotFoundError: No module named 'apt_pkg' 에러가 뜨면 Python 기본 버전을 잠시 바꿔줬다가 해보자.

update-alternatives  --set python3  /usr/bin/python3.5
# 결과: update-alternatives: using /usr/bin/python3.5 to provide /usr/bin/python3 (python3) in manual mode

sudo add-apt-repository "deb [arch=amd64] https://download.docker.com/linux/ubuntu $(lsb_release -cs) stable"

root@vicman2:/home/ywjang# update-alternatives  --set python3  /usr/bin/python3.6
# 결과: update-alternatives: using /usr/bin/python3.6 to provide /usr/bin/python3 (python3) in manual mode

경우에 따라 3.5 대신 다른 버전일 수 있다. sudo update-alternatives --config python3로 버전을 확인해보거나 기본값을 바꿔보자.

이제 설치를 진행하자.

sudo apt-get update
sudo apt-get install docker-ce docker-ce-cli containerd.io

특정 버전 설치는 apt-cache madison docker-ce로 버전을 확인 후 sudo apt-get install docker-ce= docker-ce-cli= containerd.io와 같이 설치하자.

설치 확인은 다음 hello_world를 실행해서 확인해보자.

sudo docker run hello-world

Nvidia Toolkit 설치

Container에서 GPU를 정상적으로 잘 사용하려면 nvidia toolkit를 설정해 주어야 한다.
아래 다섯 줄만 터미널에서 실행해 주자.

distribution=$(. /etc/os-release;echo $ID$VERSION_ID)
curl -s -L https://nvidia.github.io/nvidia-docker/gpgkey | sudo apt-key add -
curl -s -L https://nvidia.github.io/nvidia-docker/$distribution/nvidia-docker.list | sudo tee /etc/apt/sources.list.d/nvidia-docker.list

sudo apt-get update && sudo apt-get install -y nvidia-container-toolkit
sudo systemctl restart docker

2번째 줄에서 OK가 출력되고, 3번째 줄에서 deb 어쩌구 하는 메시지가 여러 줄 나온다. 4번째는 update와 설치가 진행되고, 5번째 줄은 docker를 재시작한다.

Docker 권한 설정

Docker를 사용하려고 하면 root 권한이 (거의) 항상 필요하다. 매번 sudo를 입력하는 것은 상당히 귀찮기 때문에 현재 접속한 user에게 권한을 주자.

sudo usermod -aG docker $USER # 현재 접속중인 사용자에게 권한주기
sudo usermod -aG docker gorio # gorio 사용자에게 권한주기

재부팅하면 권한 설정이 완료된다.

sudo reboot

이제부터 docker를 쓸 때는 sudo docker 대신 docker라고만 해도 된다.

Docker Image 다운로드

사용할 수 있는 Docker Image를 찾으려면 다음 사이트를 확인하면 된다. 이미 다운받을 곳을 알고 있다면, 해당 사이트에서 진행하자.

• Docker Hub : 웬만한 건 여기에 있다고 보면 된다.
• Pytorch : 사실 Docker Hub에 포함된다.
• Docker Registry : 직접 해 보자.

# Pytorch 최신 버전의 Docker를 받고 싶으면 아래과 같이 하자.
docker pull pytorch/pytorch:latest
# 사실 아래처럼 써도 똑같은 이미지를 받을 수 있다. 기본 tag가 latest이기 때문.
docker pull pytorch/pytorch

# Tags 탭을 누르면 여러 버전의 Docker Image를 볼 수 있다. 원하는 버전을 받아 보자.
docker pull pytorch/pytorch:1.9.0-cuda10.2-cudnn7-runtime

이미지의 이름은 <Repository> : <Tag> 의 형식을 갖는다. pytorch/pytorch가 repository 이름이고, tag는 latest가 하나의 예시이다.

참고로 CUDA 버전에 맞는 PyTorch 버전을 포함하는 Docker Image를 다운받아야 한다. 여기나 여기를 참고하면 된다.

다운받은 Image 확인

Image를 다운받았으면, 어떤 Image를 받았는지 확인해보자. 지금까지 다운받은 모든 Image들이 표시된다.

docker images

# 결과
REPOSITORY        TAG                             IMAGE ID       CREATED        SIZE
pytorch/pytorch   1.9.0-cuda10.2-cudnn7-runtime   3850639cdf7a   5 days ago     4.42GB
pytorch/pytorch   latest                          5ffed6c83695   2 months ago   7.25GB

Image 삭제

docker rmi <image_id>

이미 해당 이미지로 생성한 컨테이너가 있다면 다음과 비슷한 에러가 뜨면서 삭제가 되지 않는다.

Error response from daemon: conflict: unable to delete bd58e1ea5cd2 (must be forced) 
- image is being used by stopped container fc69401afaf6

컨테이너를 전부 제거하고 이미지를 삭제하거나, 아예 컨테이너까지 강제 삭제하려면 다음과 같이 쓰면 된다.

docker rmi -f <image_id>

모든 image를 삭제하는 방법도 있다. 물론 복구는 되지 않는다.

docker rmi $(docker images -q)

None(untagged) Image 조회 및 삭제

docker를 빌드할 때 오류 등으로 완전히 진행되지 않으면 <none> image가 생성되기도 한다. 이를 조회하고 삭제하는 방법은 다음과 같다.

docker images -f "dangling=true" -q

검색된 id를 위의 Image 삭제 명령어로 실행해도 되지만, 한 번에 삭제하는 방법이 있다.

docker rmi $(docker images -f "dangling=true" -q)
# 해당 이미지로 이미 컨테이너가 생성되었다면 -f 옵션을 쓰자.
docker rmi -f $(docker images -f "dangling=true" -q)

삭제에 관한 조금 더 자세한 내용은 여기를 참조해도 좋을 것 같다.

Container 생성 및 실행

Container 실행하는 걸 Container를 띄운다고 표현하기도 한다.

우선 Container를 Image로부터 생성해보자.

Container 생성 및 실행

docker run -it --gpus all --name prj_gorio pytorch/pytorch:1.6.0-cuda10.1-cudnn7-devel /bin/bash

# 결과
root@fcdd07478fdf:/workspace# 

위의 결과는 Container를 만들고, /bin/bash가 바로 실행되어 Container 내부에서 터미널이 열려 있는 상태라고 생각하면 된다.

옵션을 살펴보자. Ubuntu를 좀 다뤄봤으면 대충만 봐도 알 수는 있겠지만.

Container 생성 옵션

위에서 사용한 옵션을 대략 설명하면 아래와 같다.

옵션은 순서 변경이 가능하지만, Image와 실행 프로세스는 마지막에 두자.

참고 19.03 이하 버전에서는 nvidia-docker 버전에 따라 아래처럼 사용한다. nvidia-docker v2에서는 --gpus all 대신 --runtime=nvidia를 사용한다. nvidia-docker v1은 --runtime=nvidia 또는 --gpus all 명령줄 플래그 대신 nvidia-docker 별칭을 사용한다.

추가 옵션을 더 줄 수도 있다. 은근히 많으니 공식 문서를 참조하자.

Container 작동 확인

Python 라이브러리와 PyTorch GPU 사용이 가능한지 확인해 보자.

pip freeze
python -V
python

import torch

# GPU check
torch.cuda.is_available()

# GPU 정보 확인
torch.cuda.get_device_name(0)

# 사용 가능한 GPU 개수
torch.cuda.device_count()

# 현재 GPU 번호
torch.cuda.current_device()

# device 정보 반환
torch.cuda.device(0)

# 결과:
True
'TITAN Xp'
2
0
<torch.cuda.device object at 0x7f015b7f6610>

nvidia-smi는 잘 작동하는데 torch.cuda.is_available()이 안 된다면 CUDA 버전과 PyTorch 버전이 안 맞을 확률이 높다. 다른 Docker Image를 사용하자.

실행중인 Container 확인

docker ps

# 결과
CONTAINER ID   IMAGE     COMMAND   CREATED   STATUS    PORTS     NAMES

실행 중인 Container가 없으면 위처럼 별다른 정보가 나오지 않는다.

모든 Container의 리스트 확인

실행중인 Container 말고도 종료된 것까지 모두 보여준다.

docker ps -a

같은 명령어에 -a 옵션만 주면 된다. --all과 같은 의미인 것은 아마도? 알 것이다.

Container 검색

생성된 모든 컨테이너 중 특정한 Container 종류만 검색하려면 필터 옵션을 쓰면 된다.
아래 예시는 최신 pytorch docker image로 생성한 container들을 검색한다.

docker ps -a --filter ancestor=pytorch/pytorch:latest

Container 생성 후 volume 추가하는 방법

원래 생성할 때 연결하는 것이 기본이고, 안타깝게도 현재로서는 이미 생성된 docker에 간단히 volume을 추가할 수는 없다.

실수로 volume을 추가하는 것을 docker 생성 시 까먹었다면 해결할 수 있는 방법은 2가지다.

1. 어차피 연결하기 전에 수정한 사항은 그리 많지 않을 가능성이 크므로 그냥 새로 만든다.
2. 다음 코드를 실행한다.

docker commit <container-id> <newname>
docker run -ti -v <dir_in_somewhere>:/<dir_in_container> <newname> /bin/bash

• <container-id>는 docker ps -a 명령을 통해 volume을 추가하고자 하는 container id를 확인한다.
• docker commit은 아래에서 설명하겠지만 container를 통째로 저장하는 명령이다.
• <newname>은 생성할 container 백업의 이름인데 대문자는 사용 불가능하다.
• 그리고 <dir_in_somewhere>, <dir_in_container>은 각각 원하는 docker 밖 directory, docker 안 directory 경로를 지정하면 된다.

Container 관리

Container 이름 변경

실수로 --name 옵션을 안 쓰고 생성해서 임의의 이름으로 생성되었거나 이름이 마음에 안 들면 Container 이름을 간단히 바꿀 수 있다.

docker rename <old-name> <new-name>

Container 띄우기

생성 시 실행하는 것 말고, 종료 상태의 Container를 시작하려면 docker start <docker-name>과 같이 쓴다.

docker start prj_gorio

Container 접속

위의 명령은 Container를 띄운 것(구동시킨 것)이다. 실제로 접속해서 사용하려면 attach를 사용해야 한다.

docker attach prj_gorio

Container 밖으로 탈출

이 항목은 Container 생성 시 -it 옵션을 주고 생성했을 때만 가능하다.

Ctrl + P를 누르고 Ctrl + Q를 누르면 Container를 죽이지 않고 탈출할 수 있다.

Container 종료

Container를 완전히 종료하려면(삭제가 아니다!) Ctrl + D를 누르거나 다음과 같이 쓴다.

exit

Container 삭제

docker rm <container-name> [<container-name2>]
# 예시
docker rm prj_gorio
docker rm 503d22a4c01d prj_gorio ...

참고로 모든 container를 삭제하려면 다음과 같이 쓰면 된다.

docker rm -f $(docker ps -aq)

container 필터 검색과 결합하여 사용할 수도 있다.

docker rm -f $(docker ps -aq --filter ancestor=pytorch/pytorch:latest)

Container 내부 설정

Docker Image에 따라 다르지만, 기본적인 App이 설치되어 있지 않은 경우가 있다.

그런 경우에는 다음과 같이 입력하자. sudo는 쓰지 않는다.

apt-get update
apt-get install git vim wget
...

Container $\leftrightarrow$ 외부 파일 복사

docker cp <filename> <container-name>:/<path>/
# 파일명을 바꾸면서 복사하려면
docker cp <filename> <container-name>:/<path>/<filename>
# 디렉토리는 추가 옵션 없이 그냥 쓸 수 있다.
docker cp <directory-name> <container-name>:/<path>/

# 예시
docker cp gorio.py prj_gorio:/run/
docker cp gorio.py prj_gorio:/run/gorio.py
docker cp gorio.py prj_gorio:/preprocess/morio.py
docker cp gorio_test/ prj_gorio:/

Image와 Container를 파일로 저장 & 복원

Image 저장: docker save

Docker image를 tar 파일로 저장하려면 다음과 같이 쓴다.

docker save [option] <filename> [image_name]

# -o 옵션은 파일명을 지정한다.
docker save -o pytorch_latest.tar pytorch/pytorch:latest

Image 로드: docker load

docker save 명령으로 저장한 파일을 다시 Image로 불러오려면 다음과 같이 쓴다.

docker export로 생성한 tar 파일을 docker load로 불러오려고 시도하면 에러가 뜬다.

docker load -i <tar filename>

# 예시
docker load -i pytorch_latest.tar

Container 백업: docker commit -p

현재 생성되어 있는 container를 그 상태 그대로 저장하는 방법은 다음과 같다.

우선 docker commit -p 명령을 이용하여 container를 image로 만든다.

docker commit -p <container-id> <new_image_name>

그리고 위의 docker save -o 명령으로 이미지를 *.tar 파일로 만든다.

만들어진 파일을 다른 곳으로 옮긴 후 docker load -i 명령으로 이미지를 불러오면 된다.

같은 설명을 여기에서도 볼 수 있다.

참고로 8GB 이상의 파일이 있으면 commit이 안되고 Error processing tar file(exit status 1): unexpected EOF 같은 에러가 뜨니 너무 큰 파일은 굳이 container 안에 집어넣지 말고 container 생성 시 공유 옵션(--volume)을 이용하는 편이 낫다.

Container 백업: docker export

생성된 컨테이너를 파일로 저장할 수 있다.

docker export <container_name or conainter_ID> > xxx.tar

# 예시
docker export prj_gorio > gorio.tar

Container 로드: docker import

export 커맨드를 통해 만들어진 tar 파일을 다시 docker image로 생성하는 명령어이다.

docker save로 생성한 tar 파일을 docker import로 불러오려고 시도하면 에러가 뜬다.

docker import <filename or URL> [image name[:tag name]]

# 예시
docker import gorio.tar
docker import gorio.tar pytorch/pytorch:1.6.0-cuda10.1-cudnn7-devel

에러 해결법

• docker: Error response from daemon: could not select device driver "" with capabilities: [[gpu]]. - nvidia-cuda-toolkit을 설치 또는 재설치한다.
• docker: Error response from daemon: failed to create shim task: nvidia-container-cli: requirement error: unsatisfied condition: cuda>=xx.x, please update your driver to a newer version - 설치된 cuda 버전이 docker image가 요구하는 cuda version보다 낮다. cuda 또는 nvidia-driver를 버전 업그레이드한다.

참고

• CUDA 재설치 등의 작업을 수행한 경우 nvidia toolkit 작업을 다시 해 주어야 한다. 여기를 참조하면 된다.

이 글에서는 Baidu에서 만든 모델 시리즈 ERNIE 중 첫 번째(ERNIE: Enhanced Representation through Knowledge Integration)를 살펴보고자 한다.

ERNIE 시리즈는 다음과 같다. 참고로 2번째는 Baidu가 아닌 Tshinghus University에서 발표한 논문이다.

• ERNIE: Enhanced Representation through Knowledge Integration, Yu sun el al., 2019년 4월
• ERNIE 2.0: A Continual Pre-training Framework for Language Understanding, Yu Sun et al., 2019년 6월
• ERNIE-ViL: Knowledge Enhanced Vision-Language Representations Through Scene Graph, Fei Yu et al., 2019년 6월
• ERNIE-Doc: A Retrospective Long-Document Modeling Transformer, Siyu Ding et al., 2020년 12월
• ERNIE 3.0: Large-Scale Knowledge Enhanced Pre-Training For Language Understanding And Generation, Yu Sun et al., 2021년 7월

중요한 부분만 적을 예정이므로 전체가 궁금하면 원 논문을 찾아 읽어보면 된다.

ERNIE: Enhanced Representation through Knowledge Integration

논문 링크: ERNIE: Enhanced Representation through Knowledge Integration

Official Code: Github

초록(Abstract)

Novel Language Representation Model인 ERNIE(Enhanced Representation through kNowledge IntEgration)을 제안한다. BERT가 masking 전략을 쓴 것처럼, ERNIE는 phrase-level masking과 entity-level masking을 포함한 여러 knowledge masking 표현을 학습하도록 설계되었다.

• Phrase-level masking은 conceptual unit으로서 여러 단어로 구성된 전체 phrase를 masking한다.
• Entity-level masking은 여러 단어로 이루어진 entity를 masking한다.

실험 결과는 ERNIE가 자연어 추론, 의미적 유사성, 명명 개체 인식, 감정분석, 질답 등 5개의 중국어 자연어처리 과제에서 SOTA를 능가하였다. 또 cloze test에서 더 강력한 지식 추론 능력을 가진다.

얘가 Ernie이다. ELMo 이후로 세서미 스트리트에 끼워맞추는 게 유행..

BERT가 강력한 파괴력을 가졌던 것처럼, 중국 바이두에서 만든 이 모델을 Ernie 시리즈로 밀고 나간다. GLEU benchmark 등 영어에서도 실험하지만, 만든 곳이 그 곳이니만큼 중국어에 상당 부분 초점이 맞춰져 있다.

1. 서론(Introduction)

이전까지 언어표현 사전학습 모델은 동시에 등장하는 단어들을 바탕으로(co-occurence) 학습을 진행해 왔다. Word2vec 등이 단어표현에서 대표적인 예시이고, ELMo, BERT 등의 연구에서는 여러 전략을 사용하여 단어표현을 발전시키고 downstream task에 더욱 효율적이게 만들었다.

이러한 모델들의 대부분은 단지 문맥 안에서 masking된 단어를 예측하는 방식으로 진행되는데 이는 문장에 대한 사전 지식을 고려하지 않는다. 예를 들어 “Harry Potter is a series of fantasy novels written by J. K. Rowling”이라는 문장에서, Harry Potter는 소설 이름, J.K. Rowling은 작가 이름이다. Harry Potter를 masking해서 지웠을 때 (사람은) 빠진 단어가 무엇인지 쉽게 유추할 수 있지만 모델은 Harry Potter와 J.K. Rowling의 관계를 알지 못하며 예측하지 못한다. 여기서 모델이 만약 사전지식을 더 잘 알 수 있다면, 언어표현을 더욱 유용하게 만들 수 있다고 생각할 수 있다.

이 논문에서, knowledge masking 전략을 사용한 ERNIE를 소개한다. 기본적인 masking 전략에 더해 entity-level masking과 phrase-level masking을 사용한다. Phrase를 하나의 entity로 취급하여 사용하는 방식으로 학습하며 학습 내내 하나의 entity처럼 사용된다. 이 방식으로, entity와 phrase에 대한 사전지식이 암묵적으로 학습된다. ERNIE는 knowledge를 명시적으로 입력받지 않고 암묵적으로 학습하고 더 긴 의미적 의존성을 파악함으로써 더 나은 일반화 및 적응 능력을 가질 수 있다.

학습 비용을 위해서 5가지 중국어 NLP task에서 사전학습을 진행하며, 대부분에서 SOTA 결과를 달성했다.

이 논문의 기여한 바는,

1. Entity와 Phrase를 하나의 unit으로 취급하여 masking하고 학습하는 방식으로 문맥적, 의미적 정보를 암묵적으로 학습하는 새로운 언어모델을 제시하였다.
2. ERNIE는 다양한 중국어 NLP task에서 SOTA 결과를 달성하였고,
3. ERNIE의 코드와 사전학습된 모델을 공개하였다.

2. 관련 연구(Related Work)

Context-independent Representation

단어표현을 연속적인 벡터로 표현하는 방식은 긴 역사를 가지고 있다. 2003년 NNLM에서는 MLP를 사용하여 단어 벡터표현을 학습하였다.
전통적인 방법은 문맥과 독립적으로 학습하는 방식으로 WordVec, Glove 등이 있다. 이들은 대규모 말뭉치를 입력으로 받고 수백 차원 정도의 단어표현을 학습하며 각 단어에 대해 하나의 embedding 표현을 생성한다.

Context-aware Representation

그러나, 문맥을 고려하지 않고서는 완전한 단어표현을 학습할 수 없다. 각 단어는 문맥에 따라서 다양한 의미를 갖기 때문이며 Cove, ELMo, BERT, GPT2 등에서는 문맥을 고려하여 단어표현을 생성하도록 했다.

Heterogeneous Data

다차원적 비지도 데이터에서 사전학습한 의미적 encoder는 전이학습 성능을 높일 수 있다. Universal sentence encoder(Cer et al., 2018), XLM(Lample and Conneau, 2019)이 Wikipedia 등에서 학습하여 여러 MT task에서 좋은 성능을 보였다.

3. Methods

모델의 Transformer encoder는 3.1절, Knowledge Integration은 3.2절, BERT와 ERNIE의 비교는 아래 그림을 참조한다.

BERT는 각 단어를 일정 확률로 masking하고 이를 예측하지만, ERNIE는 단어뿐 아니라 독립체(entity), 구(phrase) 전체를 하나의 unit으로 취급하여 masking한다.

3.1. Transformer Encoder

ERNIE는 GPT, BERT, XLM처럼 multi-layer Transformer를 기본 인코더로 사용한다. Transformer는 self-attention을 통해 각 token의 문맥 정보를 잡아낼 수 있고 문맥적 embedding의 sequence를 생성한다.

중국어 말뭉치를 위해, CJK Unicode range에 있는 모든 문자 주변에 공백을 추가하고 WordPiece tokenizer를 사용하였다. 주어진 token에 대해서 그 입력 표현은 주변 token, segment & position embedding(잘 모르겠으면 BERT 참고)의 embedding을 더하여 구성한다. 첫 번째 token은 [CLS]이다.

3.2. Knowledge Integration

사전지식을 사용하는데, 이를 직접 집어넣지는 않고, entity와 phrase 수준 지식을 통합하기 위해 다단계 knowledge masking 전략을 제안한다. 문장에서 여러 masking 수준은 Figure 2에서 볼 수 있다.

3.2.1. Basic-Level Masking

기본 단위(영어는 한 단어, 중국어는 한 글자)을 학습하는 단계로 15%의 기본 단위를 임의로 masking하고 Transformer는 이를 예측하도록 한다. 여기서는 고수준의 의미 정보를 얻기는 힘들다.

3.2.2. Phrase-Level Masking

여러 단어나 글자를 하나의 개념적 단위로 묶은 것으로 영어는 어휘분석과 chunking, 언어의존적 분할 도구를 사용하여 단어/phrase 정보를 얻는다. 이 단계에서는 한 phrase 안에 속하는 모든 단어(글자)를 한 번에 masking한다. 이를 통해 phrase 정보가 단어 임베딩에 포함된다.

3.2.3. Entity-Level Masking

Name Entity는 사람, 지역, 조직, 상품 등을 포함하며 적절한 “이름”으로 나타내어진다. 추상적이거나 물리적 실체를 가질 수도 있다. 보통 entity는 문장에서 중요한 정보를 갖는다. Phrase 단계와 비슷하게 named entity가 문장에서 어떤 것이 있는지 분석하고 masking할 때는 한 entity 안에 속하는 모든 단어/글자를 한 번에 masking하고 이를 예측하도록 학습한다.

4. Experiments

ERNIE는 비교를 위해 Bert-base와 같은 모델 크기를 갖는다. 12 Encoder layers, 768 hidden units, 12 attention heads를 포함한다.

4.1. Heterogeneous Corpus Pre-training

중국 Wikipedia, Baidu Baike/News/Tieba 말뭉치를 사용하였으며 각 문장 수는 21M~54M이다. 각각 언어모델링의 기초가 되는 백과사전 글과 영화/배우 이름 등에 대한 정보, Reddit과 같은 토론, DLM의 것과 같은 내용을 포함한다. 한자는 번체에서 간체로, 영어는 소문자로 변환하고 17,964개의 공유 유니코드 문자를 포함한다.

4.2. DLM

Dialogue Language Model의 약자로 BERT의 token-position-segment embedding과 비슷한 구조를 가지지만, segment embedding이 2개의 문장을 뜻하는 0, 1이 아닌 multi-turn 대화를 나타내도록 되어 있다(Question-Response-Question 등. QRQ, QRR, …)
이는 ERNIE가 대화에서 암묵적인 관계를 학습할 수 있게 한다.

4.3. Experiments on Chinese NLP Tasks

5가지 task에 대해 진행하였다.

1. 자연어추론: XNLI(Cross-lingual NLI) 말뭉치는 모순, 중립, 함의를 포함하며 중국어 포함 14개 언어 쌍이 있다.
2. Semantic Similarity: LCQMC 데이터셋 사용, 두 문장이 같은 내용(intention)을 포함하는지를 판별하는 task.
3. Name Entity Recognition: Microsoft Research Asia에서 배포한 MSRA-NER 데이터셋 사용. 사람/장소/조직 이름 등을 포함하는 entity를 갖고 있으며 sequence labeling task로도 볼 수 있다.
4. Sentiment Analysis: ChnSentiCorp 데이터셋 사용. 호텔, 책, 전자컴퓨터와 같은 여러 domain의 comment를 포함하며 어떤 문장의 긍정/부정을 평가한다.
5. Retrieval Question Answering: NLPCC-DBQA 데이터셋 사용. 질문에 맞는 답을 선택하는 것이다. 평가 방법은 MRR과 F1 score 사용.

4.4. Experiment results

ERNIE가 모든 task에서 BERT를 능가한다. 중국어 NLP task에서는 SOTA를 찍고, BERT에 비해서 절대오차 1% 이상으로 우세하다. 이러한 이득은 지식 통합 전략에 따른 것이다.

4.5. Ablation Studies

Knowledge Masking 전략의 효과를 알아보기 위해 전체의 10% 학습 데이터를 뽑고, 각 level(word/phrase/entity)의 masking 전략 중 어느 것을 적용하는지에 따라 성능 차이가 좀 난다. phrase와 entity 수준에서 masking을 하는 것이 성능이 더 좋은 것을 볼 수 있다. 전체 데이터셋을 사용하면 10%일 때에 비해 0.8%의 향상이 있다.

DLM을 학습에 포함시키는 경우 그렇지 않은 경우에 비해 0.7%/1.0%의 향상이 있다.

4.6. Cloze Test

Name Entity를 단락에서 제거하고 모델이 이를 추론하는 Cloze test를 진행하였다. BERT는 문장에서 복사하려고 한 반면에 ERNIE는 기사에서 언급된 지식 관계를 기억하고 있다거나(Case 1), BERT는 entity 종류는 맞췄지만 제대로 채우는 데에는 실패했다거나(Case 2,5), 빈 칸을 여러 글자로 채웠지만 의미는 맞추지 못했다거나(Case 3, 4, 6) 하는 예시가 있다. 중국어라서 봐도 잘은 모르겠지만..(ERNIE는 Case 4에서 맞추지는 못했지만 semantic type은 맞췄다고 한다.)

결론(Conclusion)

지식 통합 전략으로 지식을 사전학습 언어모델에 넣는 새로운 방법을 제시했다. 5가지의 중국어 NLP task에서 BERT보다 우수한 성능을 보였으며 지식통합과 사전학습이 언어표현 학습에 모두 도움이 되는 것을 확인하였다.
이후에는 다른 종류의 지식을 의미적 표현모델에 넣는 방법(구문 parsing, 약한 지도학습 등)과 다른 언어에 적용할 방법을 연구한다고 한다.

참고문헌(References)

논문 참조!