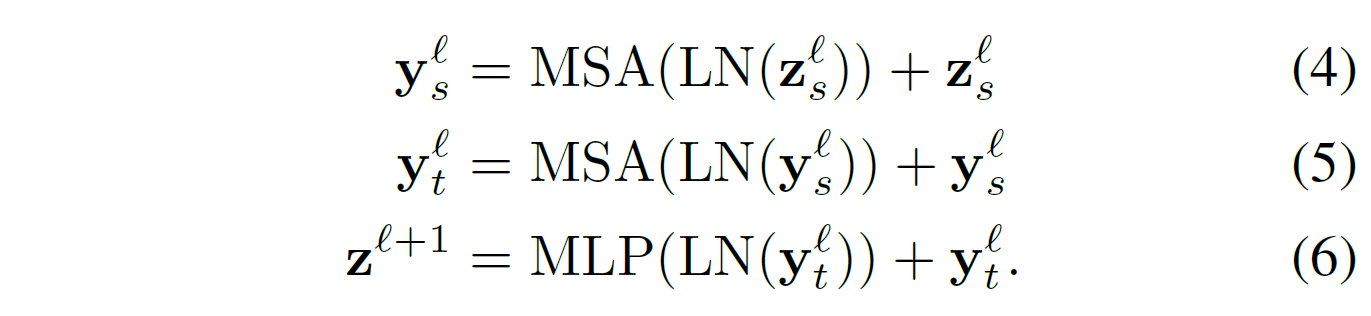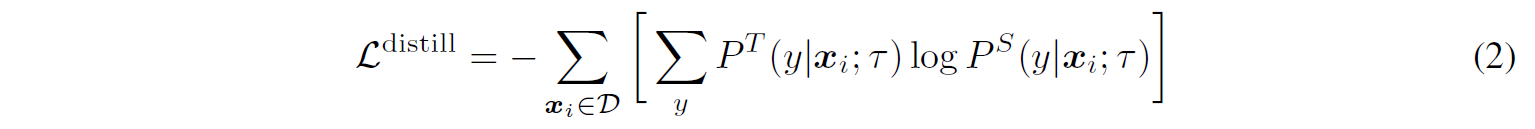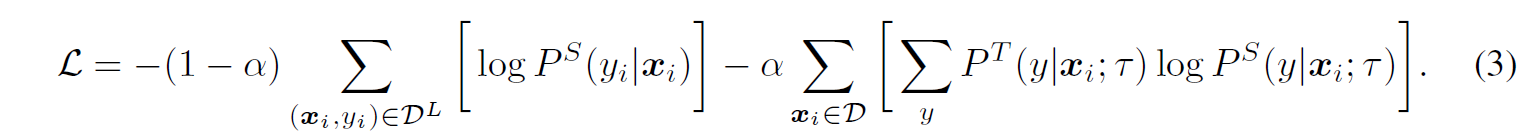이 글에서는 ViT(Vision Transformer) 논문을 간략하게 정리한다.

ViT(An Image is Worth 16x16 Words: Transformers for Image Recognition at Scale)

논문 링크: An Image is Worth 16x16 Words: Transformers for Image Recognition at Scale

Github: https://github.com/google-research/vision_transformer

• 2020년 10월, ICLR 2021
• Google Research, Brain Team
• Alexey Dosovitskiy, Lucas Beyer, Alexander Kolesnikov, Dirk Weissenborn, et al.

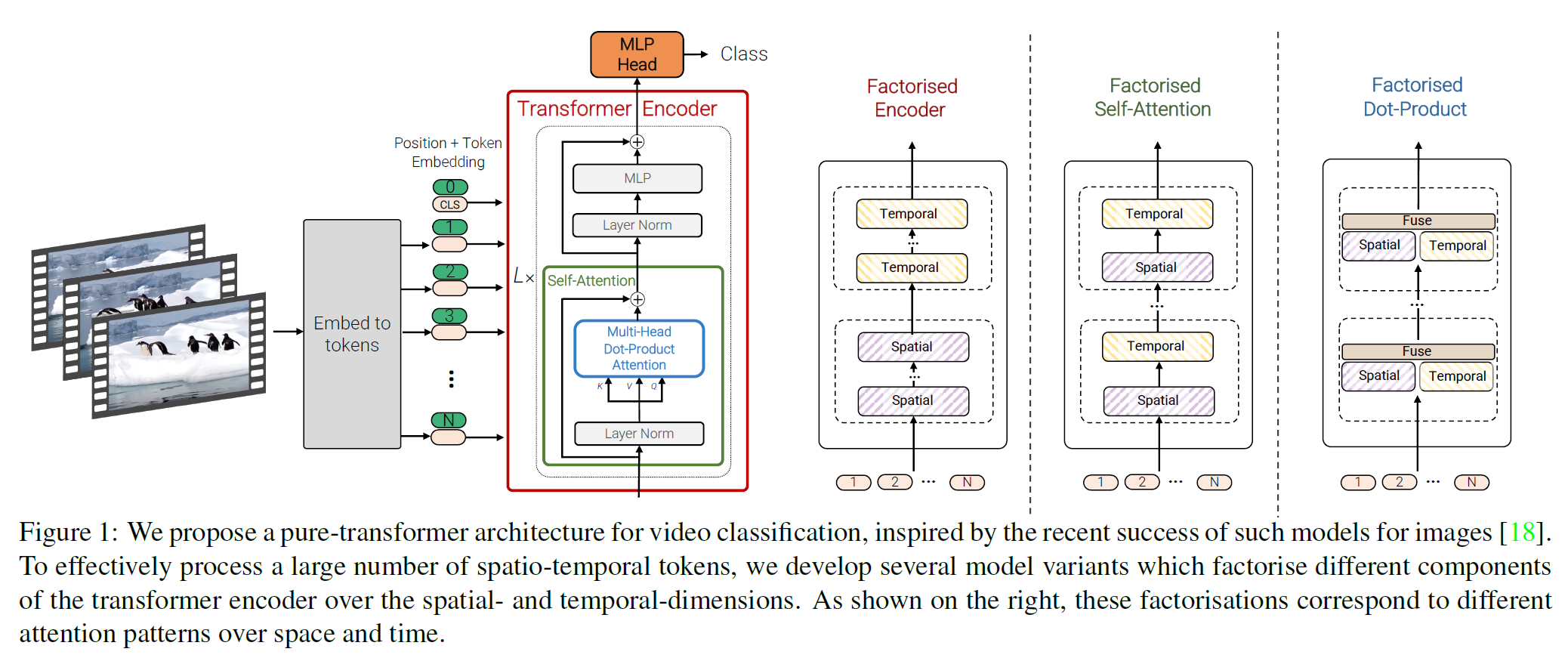
이미지 class 분류를 위해 이미지를 여러 patch로 잘라 Transformer에 넣는 방법을 제안한다.

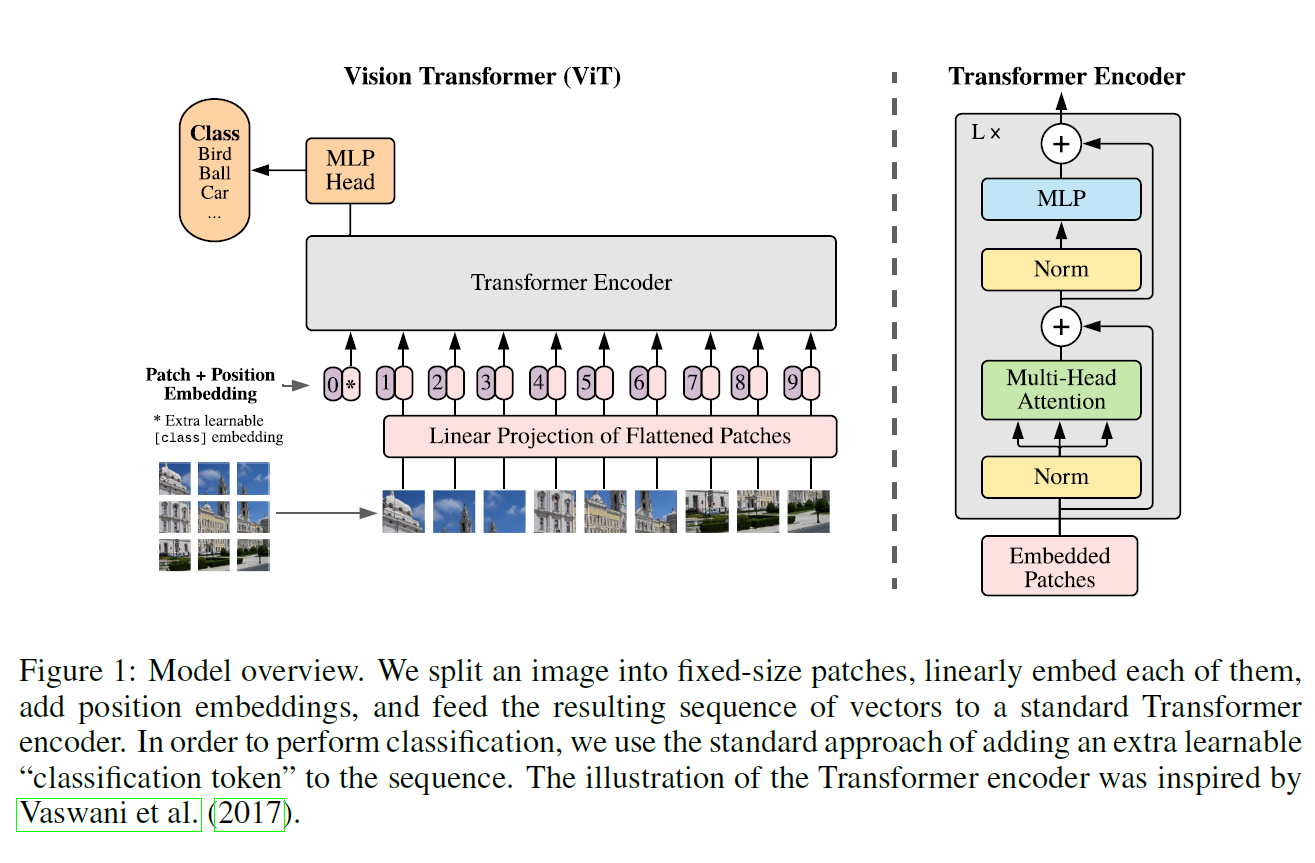
전체 구조를 순서대로 따라가보자. 왼쪽 아래에서부터 출발한다.

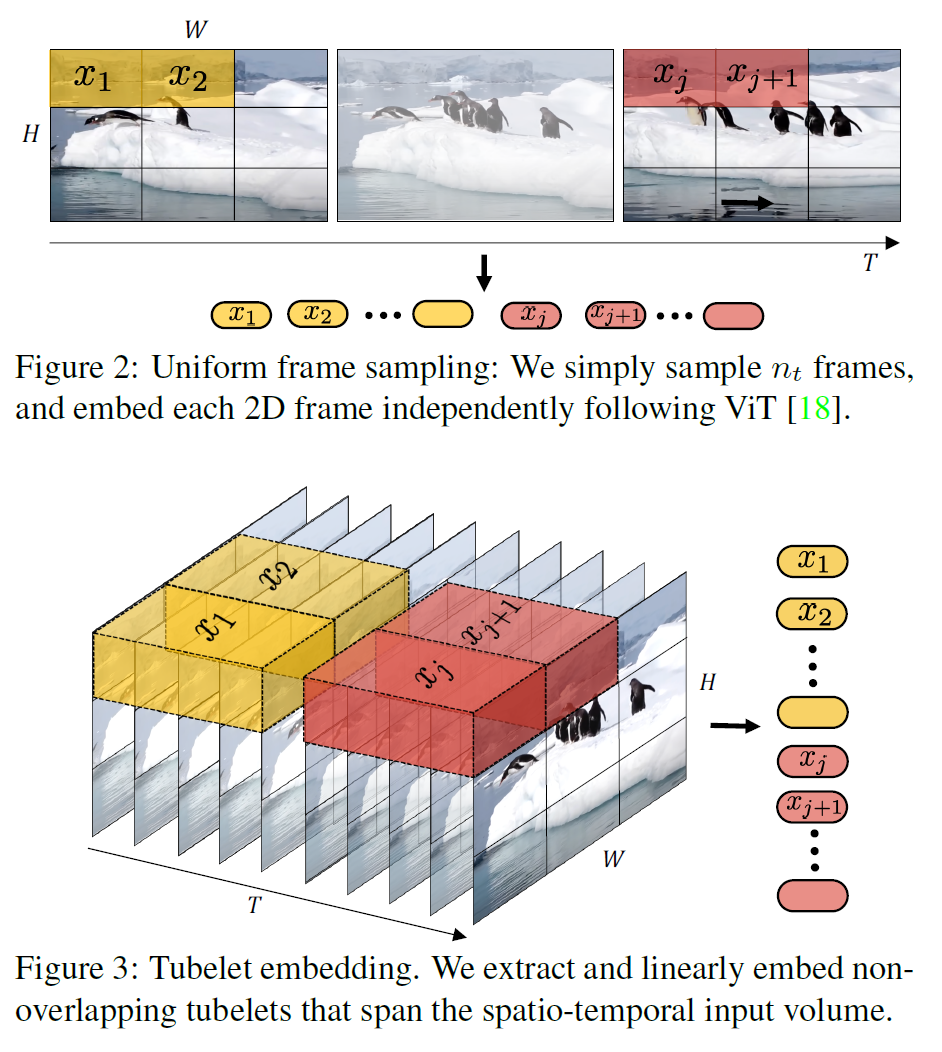
1. 이미지를 16 x 16 크기의 patch로 나눈다. 자연어에서 word token sequence가 주어지는 것처럼, 여기서는 이미지를 16 x 16크기의 token으로 취급한다.
   • 이미지 크기가 224 x 224라면 총 196($=N$)개의 patch가 생긴다.
2. 이 patch들의 linear embedding을 Transformer에 입력으로 주어야 하는데, 그 전에
   • [CLS] token embedding이 맨 앞에 추가된다.
   • Linear Embedding을 구하는 것은 Linear Projection $E \in \mathbb{R}^{(P^2C)\times D}$ 를 통해 가능하다.
     • 입력의 차원 변화는 $P^2C \rightarrow D$이다.
     • 여기서 $C=3, D=1024$를 사용했다.
   • 여기까지 보면, word를 embedding으로 바꿔서 Transformer에 입력으로 주는 것과 거의 동일한 과정이다.
   • Patch Embedding에 더해 Position Embedding이란 것을 추가하는 것을 볼 수가 있다. 이는 Transformer나 BERT에서 위치 정보를 추가해 주는 것과 같은 과정이다.
     • $E_{pos} \in \mathbb{R}^{(N+1)\times D}$을 곱한다. 이미지 patch 개수 $N$에 [CLS]를 더해 총 $N+1$개에 position embedding을 불인다.
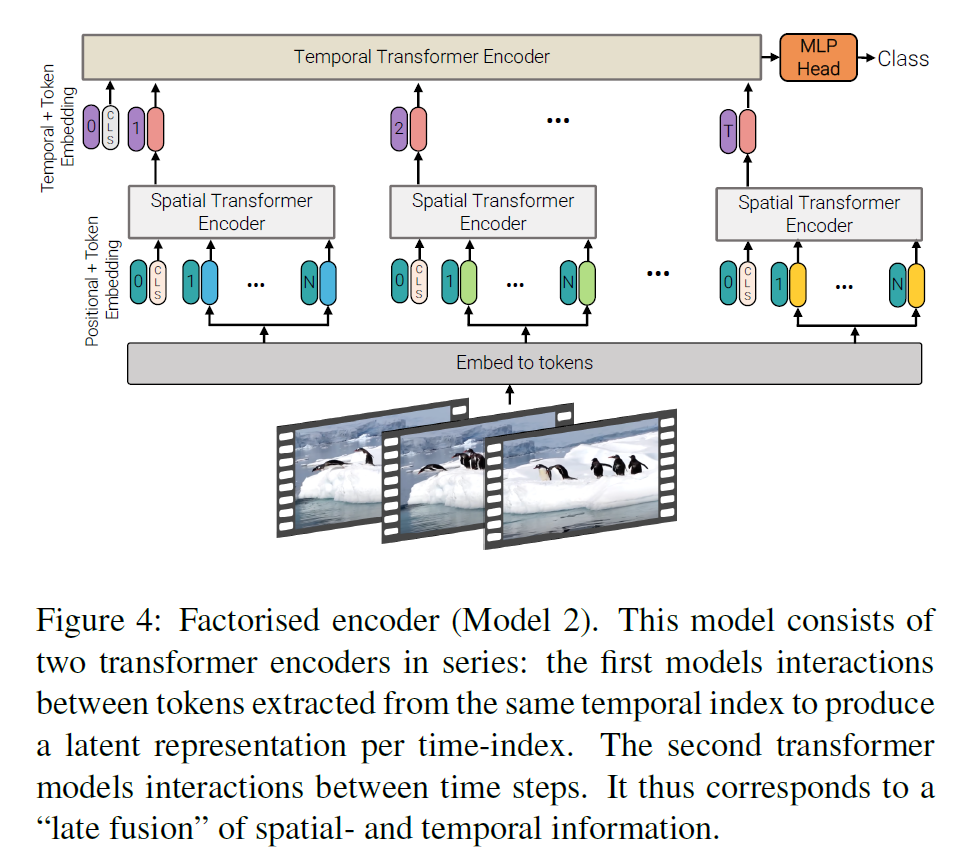
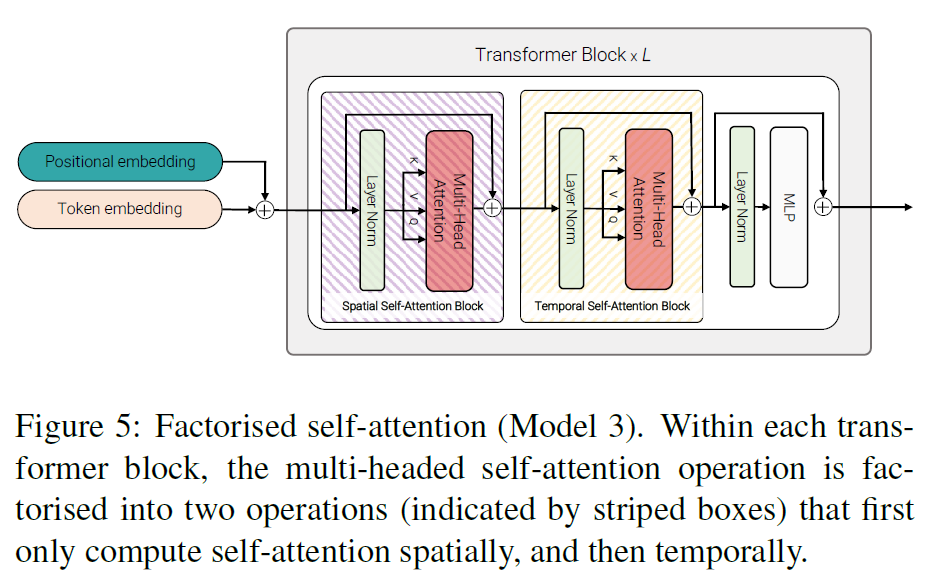
3. Transformer에 이 embedding들을 태우는데 Transformer는 Norm이 맨 앞으로 온 것을 빼면 똑같은 구조를 사용한다.
4. 그리고 input image를 분류하기 위해 MLP에 태운다. 이 과정을 통해 이미지 분류를 수행할 수 있다.
   • MLP는 아래 식을 따른다. 여기서 MSA는 Multi-head Self-Attention이다.

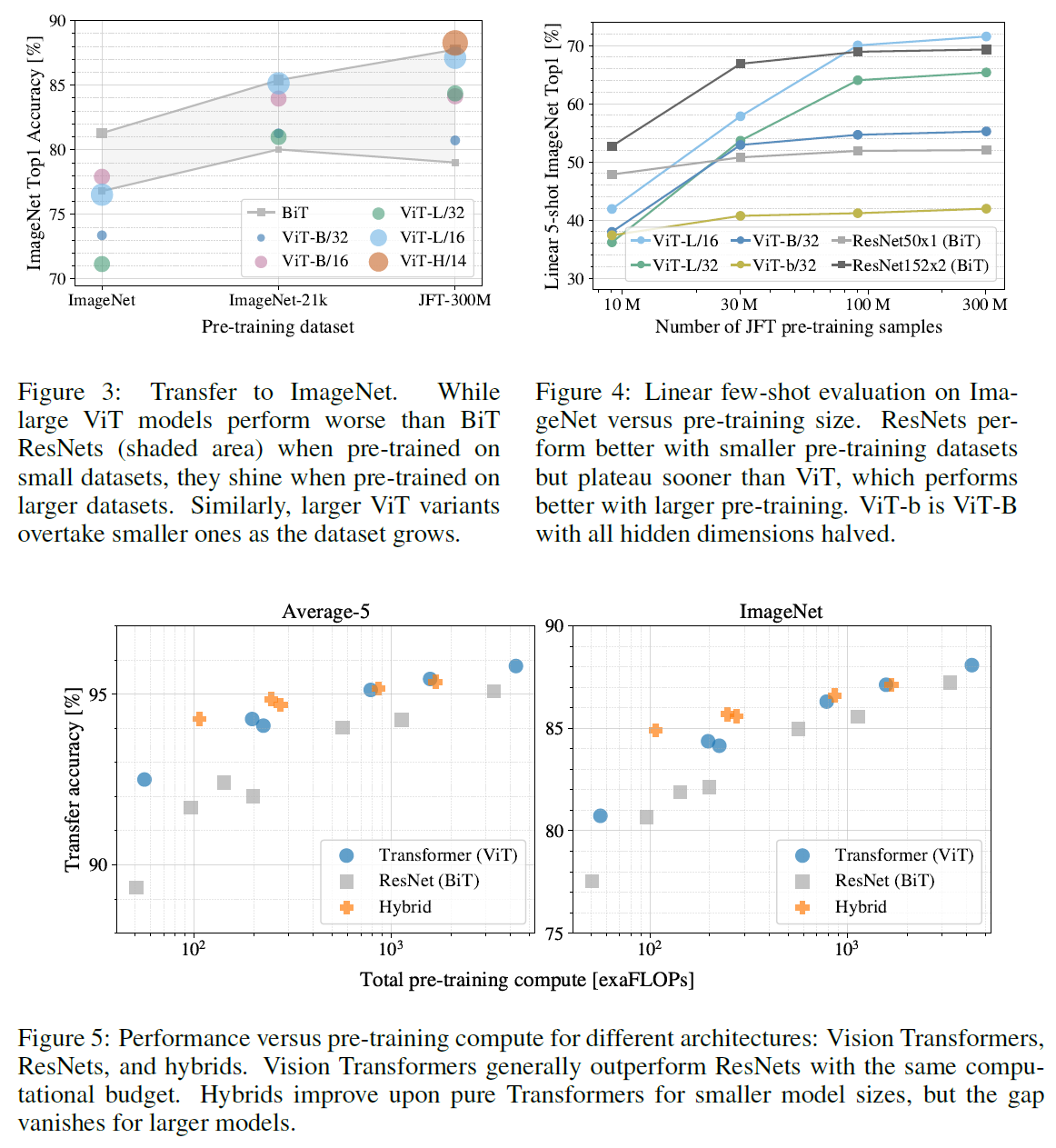
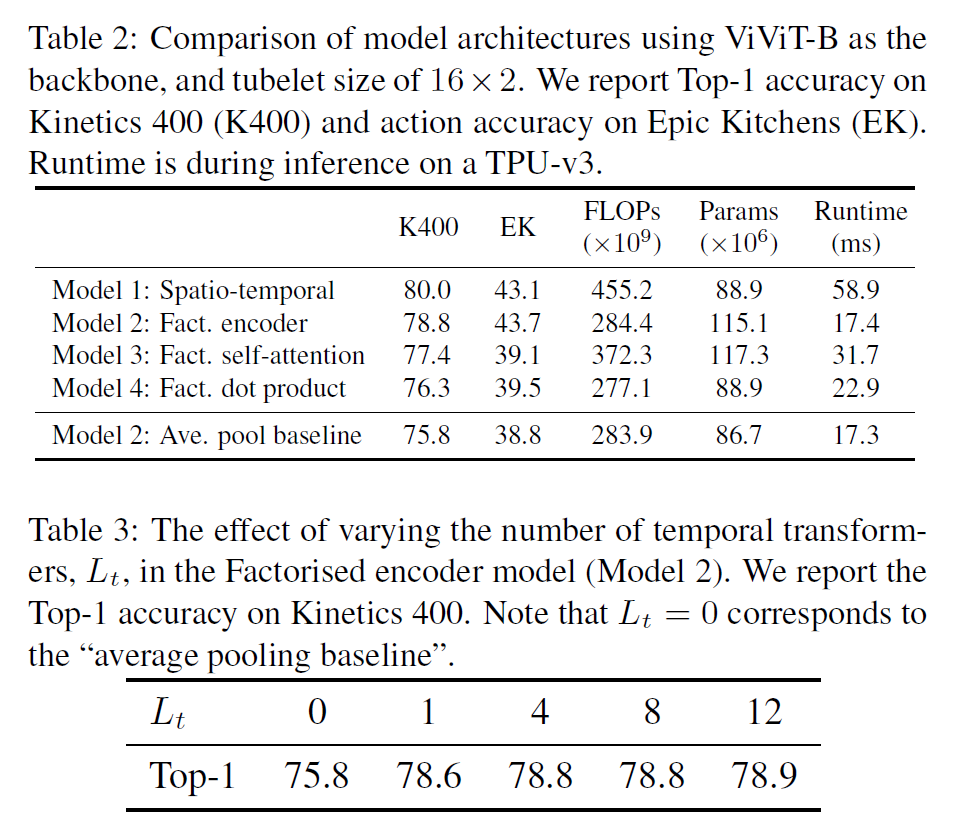
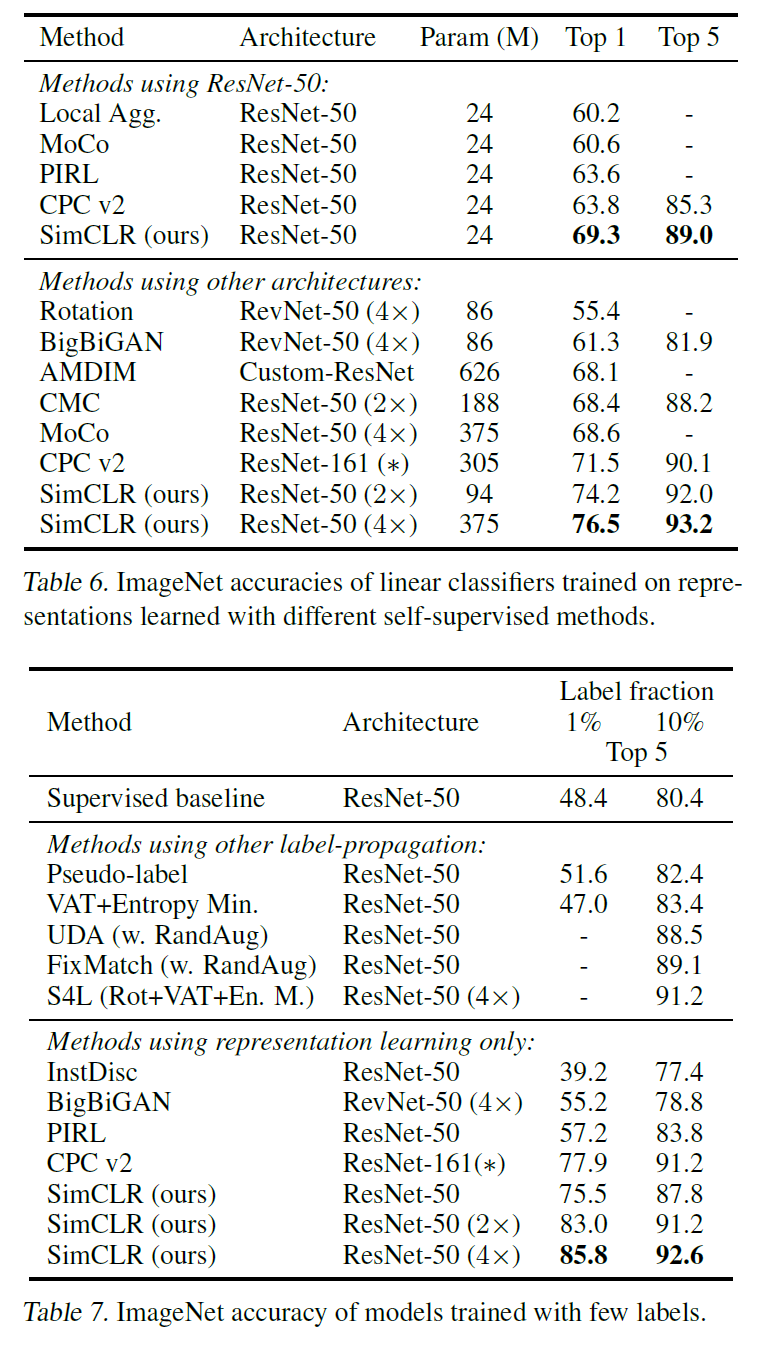
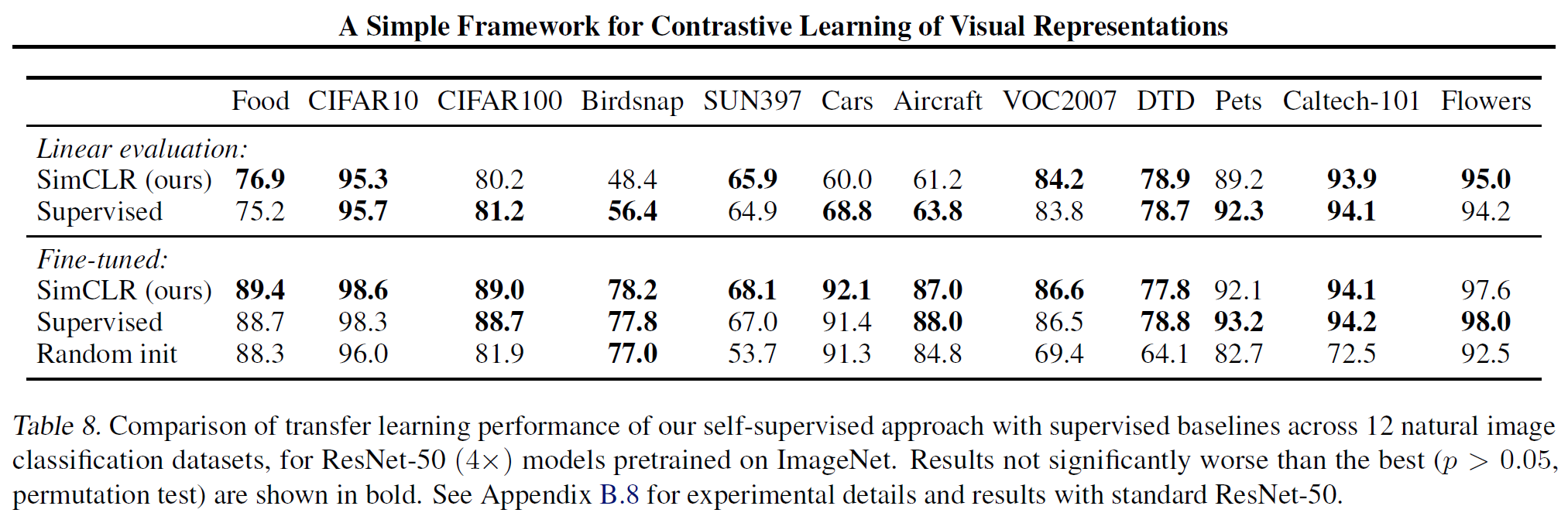
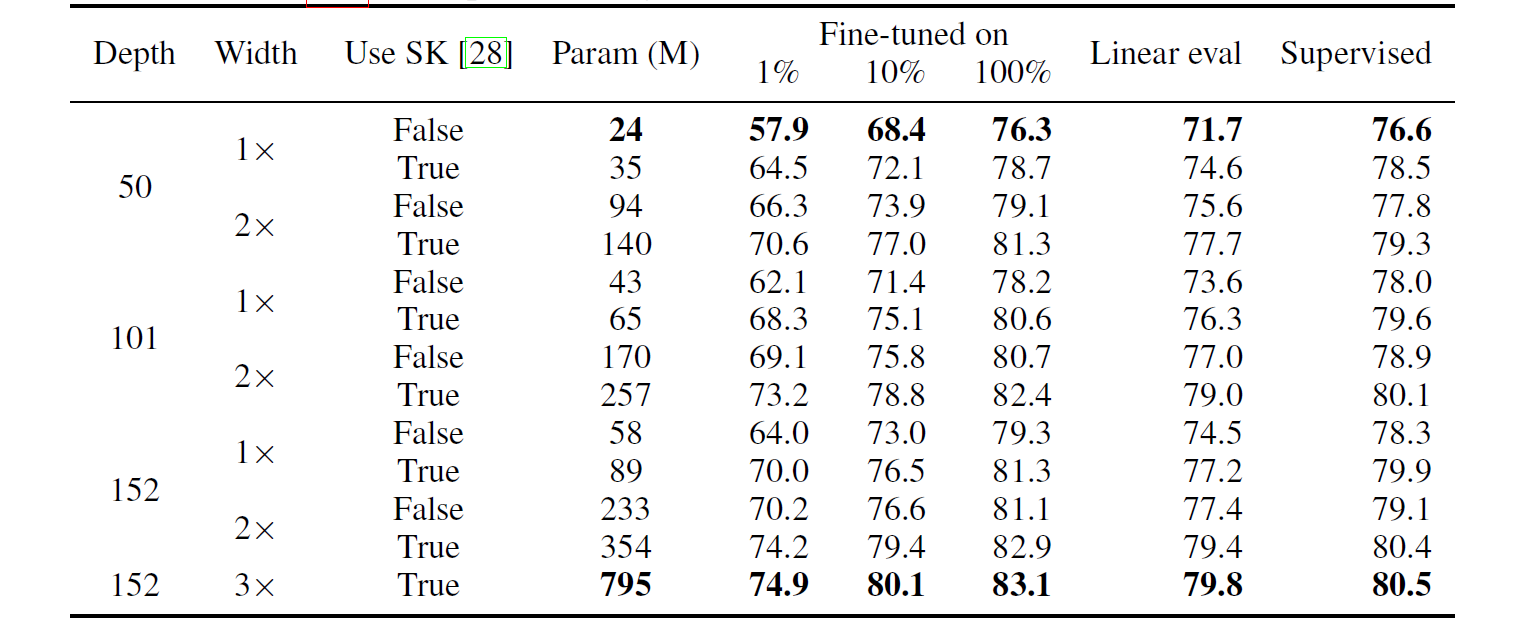
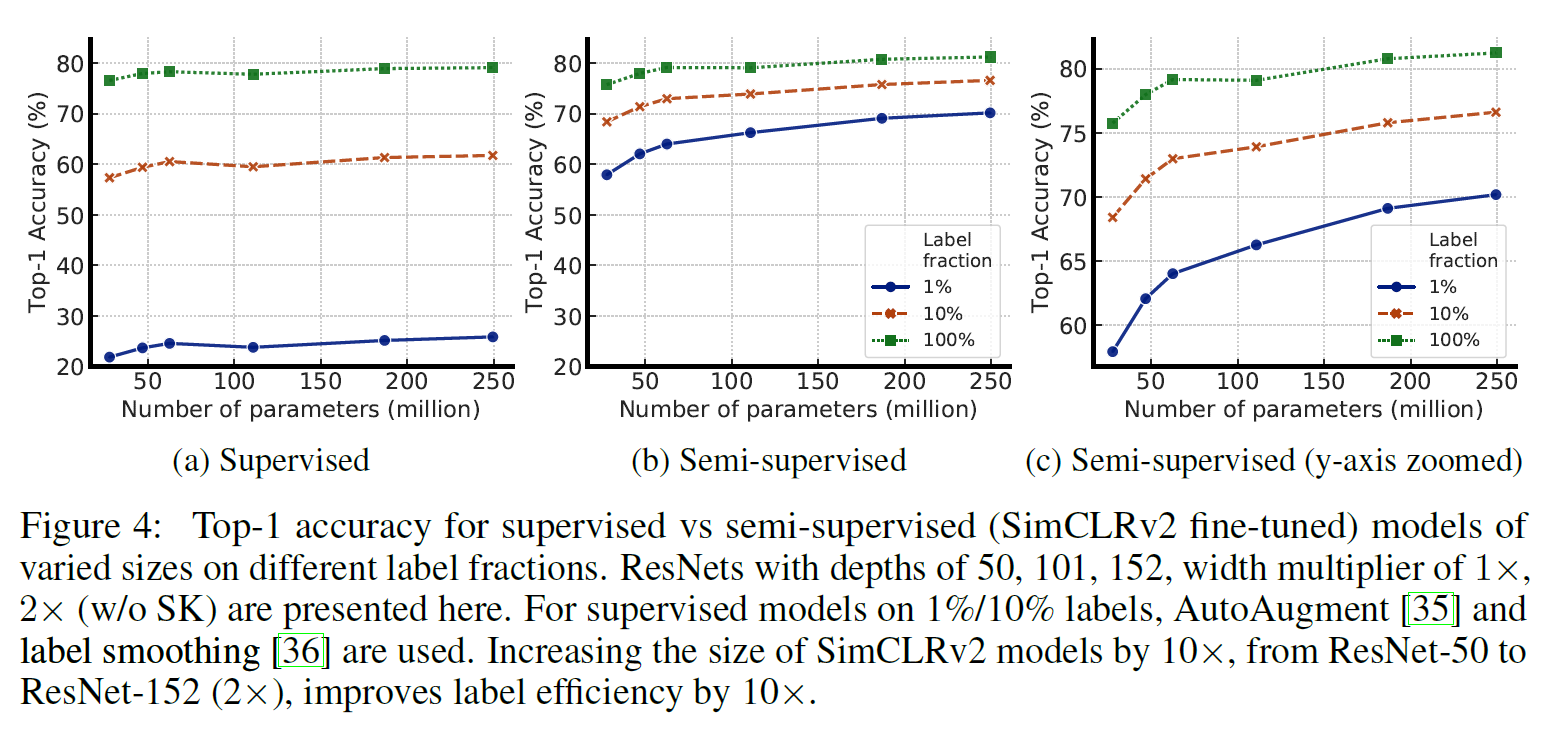
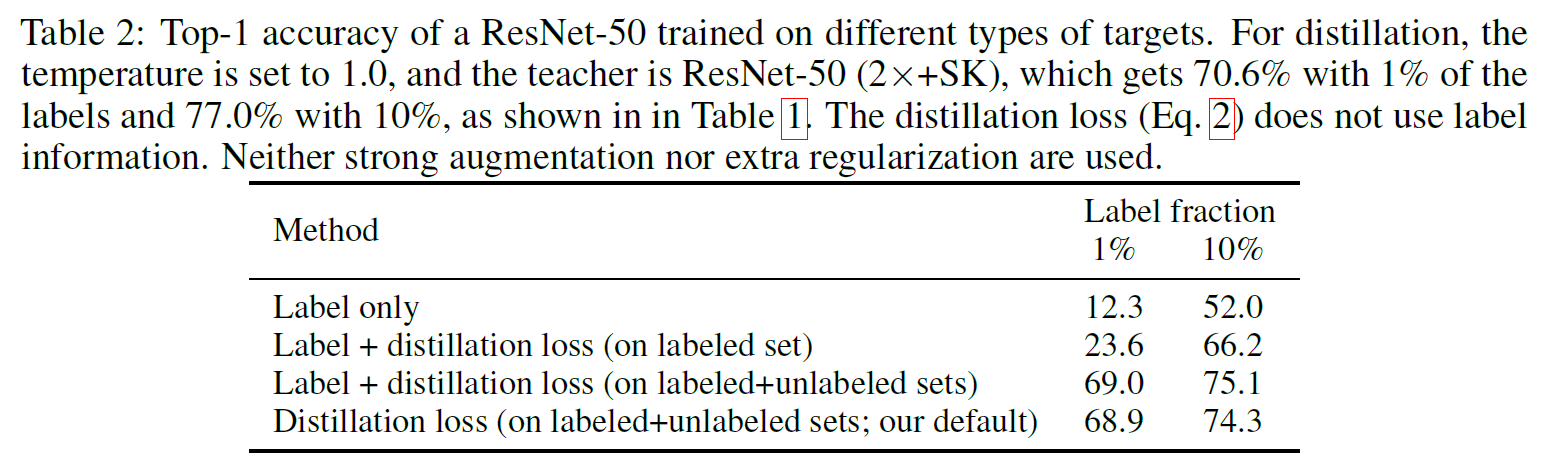
실험 결과는 다음과 갈다.

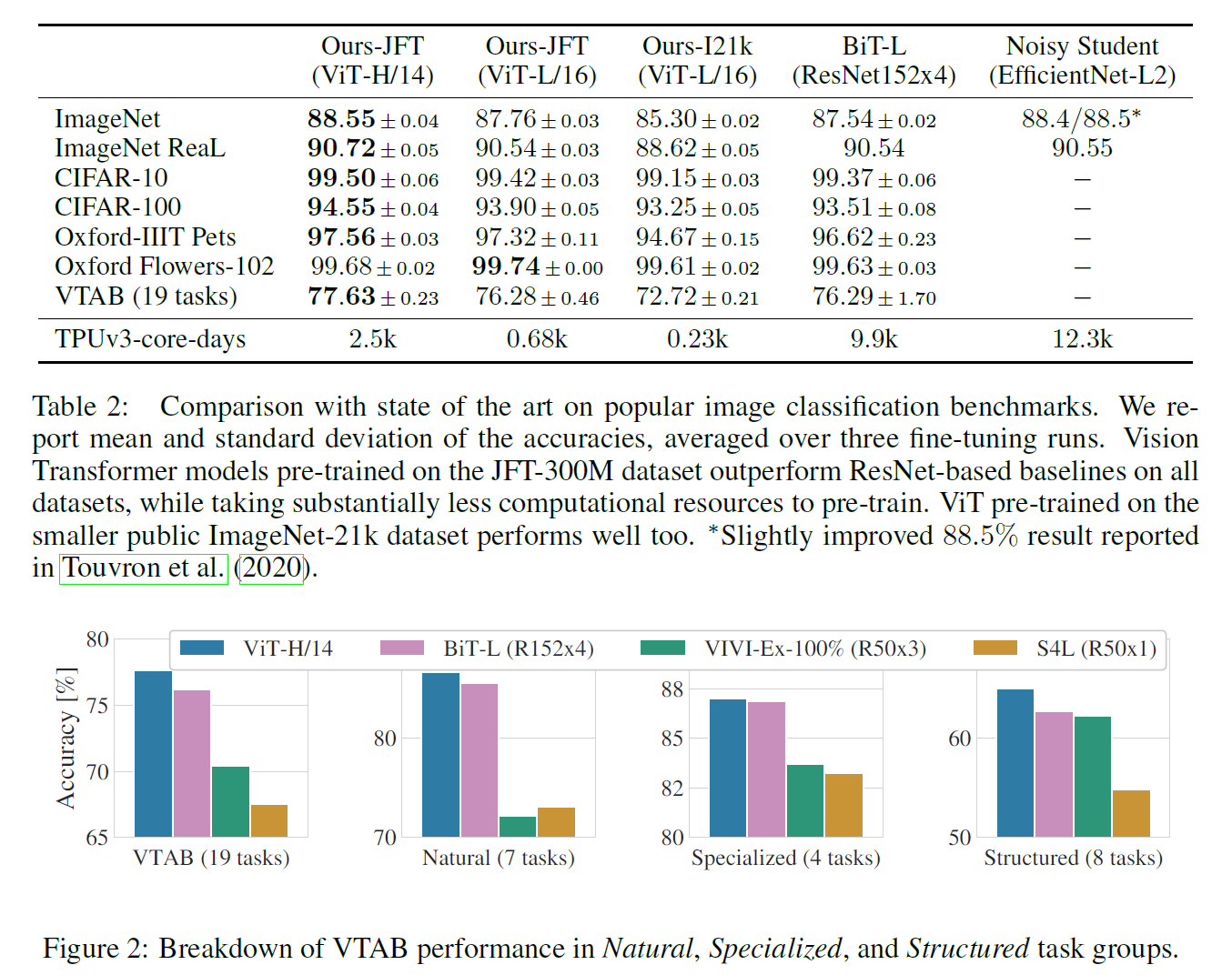
이 논문의 강점은,

• 꽤 많은 일반적인 데이터셋에서 좋은 성능을 보인다.
• Image를 Transformer에 적용시켰다는 점에서 아이디어를 높이 살 수 있다.
• 데이터가 많기만 하다면 spatial locality를 넘어 더 많은 어떤 feature를 잡아낼 수 있다.

단점은,

• 계산량이 매우 많다.
• JFT-300M과 같이 매우 큰 데이터셋에서 학습했을 때에만 잘 동작한다.
• 이미지를 patch로 잘라서 일렬로 집어넣기 때문에 spatial info(inductive bias)를 활용하지 못한다. 작은 데이터셋에서 결과가 잘 나오지 않는 이유이기도 하다.

가장 작은 데이터셋인 ImageNet에서 성능이 가장 좋지 않다는 점을 아래 결과에서 확인할 수 있다.

이 글에서는 Transformer를 기반으로 Vision 문제를 푸는 모델인 ViViT(Video ViT: ViViT - A Video Vision Transformer), MTN, TimeSFormer, MViT 논문을 간략하게 정리한다.

ViT(An Image is Worth 16x16 Words: Transformers for Image Recognition at Scale)

논문 링크: An Image is Worth 16x16 Words: Transformers for Image Recognition at Scale

Github: https://github.com/google-research/vision_transformer

• 2020년 10월, ICLR 2021
• Google Research, Brain Team
• Alexey Dosovitskiy, Lucas Beyer, Alexander Kolesnikov, Dirk Weissenborn, et al.

ViT에 대한 설명은 여기를 참고하자.

Video transformer network

논문 링크: Video transformer network

VTN 논문에서는 사전학슬된 ViT 위에 tempoarl attention encoder를 추가하여 Video Action Recognition에서 좋은 성능을 내었다.

ViViT: A Video Vision Transformer

논문 링크: ViViT: A Video Vision Transformer

Github: https://github.com/google-research/scenic/tree/main/scenic/projects/vivit

• 2021년 3월, ICCV 2021
• Google Research
• Anurag Arnab, Mostafa Dehghani, Georg Heigold, Chen Sun, Mario Lučić, Cordelia Schmid

위의 ViT 논문의 아이디어를 그대로 가져와 Video에 적용한 논문이다.

1. 비디오의 각 frame을 $n_w \times n_h$ patch로 나누어 각 patch들은 Transformer Encoder에서 contextualize된다.
   • $n_h$: # of rows
   • $n_w$: # of columns
   • $n_t$: # of frames
2. 그러나 attention 계산량이 매우 많다.
   • 총 patch 수가 ($n_t \times n_h \times n_w$)
   • 따라서 계산은 ($n_t^2 \times n_h^2 \times n_w^2$)
3. 따라서 전체 frame 대신 일부만 균등선택하여 계산한다(uniformly frame sampling)
   • 또한 Tubelet embedding을 사용한다. 토큰화 중에 미리 spatio-temporal info를 합친 다음 계산하면 계산량을 줄일 수 있다.

이 논문에서는 생각할 수 있는 여러 개의 모델을 설명한다. 하나씩 살펴보자.

Model 1: Spatio-temporal attention

사실상 brute-force 모델에 가깝다. 모든 spatio-temporal token을 forward한다.

Model 2: Factorised encoder

• 모든 spatio-temporal token에 대해 계산을 진행하는 대신, 일단 spatio token에 대해서만 계산을 진행한다(by ViT).
• 각 frame을 embedding으로 바꾼 뒤 Temporal Transformer Encoder에 태운다.
• 이러면 계산량은 다음과 같다: $(n_h^2n_w^2 + n_t^2)$

Model 3: Factorised self-attention

• 모든 token 쌍에 대해 Multi-head Self-attention을 수행하는 대신, 먼저 spatial 부분에 대해 self-attention을 수행한다. 그리고 Temporally하게 self-attention을 수행한다.
• Naive model(Model 1)과 같은 수의 Transformer layer를 갖는다.
• [CLS] token은 사용되지 않는다.

Factorisesd self-attention은 다음과 같이 정의된다.

Model 4: Factorised dot-product attention

Transformer가 multi-head 연산을 포함한다는 것을 기억하자.

• 절반의 attention head는 spatial한 부분을 key, value로 다룬다. (Spatial Head)
  • $\mathbf{K}_s, \mathbf{V}_s \in \mathbb{R}^{n_h \cdot n_w \times d}, \quad \mathbf{Y}_s = \text{Attention}(\mathbf{Q}, \mathbf{K}_s, \mathbf{V}_s)$
• 나머지 절반은 같은 temporal index에서 key, value를 다룬다. (Temporal Head)
  • $\mathbf{K}_t, \mathbf{V}_t \in \mathbb{R}^{n_t \times d}, \quad \mathbf{Y}_t = \text{Attention}(\mathbf{Q}, \mathbf{K}_t, \mathbf{V}_t) $

위의 연산을 수행한 뒤 최종 결과는

[\mathbf{Y} = \text{Concat}(\mathbf{Y}_s, \mathbf{Y}_t)\mathbf{W}_O]

이 된다.

Experiments

ViT가 매우 큰 데이터셋에서만 좋은 결과를 얻을 수 있었기 때문에, ViT를 initialization으로 사용하였다.

위의 모델들을 실험한 결과는 다음과 같다. 또한, Temporal Transformer의 layer 수에 따라서도 Top-1 Accuracy를 측정한 결과도 있다.

결과가 약간 의외(?)인데, Model 1이 가장 연산이 비싸지만 성능은 제일 좋다. Model 2는 성능이 살짝 낮지만 연산량 대비해서는 꽤 효율적이라 할 수 있다.

TimeSFormer: Is Space-Time Attention All You Need for Video Understanding?

논문 링크: Is Space-Time Attention All You Need for Video Understanding?

Github: https://github.com/facebookresearch/TimeSformer

• 2021년 6월, ICMl 2021
• Facebook Research
• Gedas Bertasius, Heng Wang, Lorenzo Torresani

Facebook에서 만든 논문인데 위의 ViViT와 거의 비슷하다. ViT를 Video에 적용시킨 논문이다.

Multiscale vision transformers

논문 링크: Multiscale vision transformers

MViT는 scratch로부터 학습된 video recognition 모델로 spatio-temporal 모델링을 위해 pooling attention을 취함으로써 계산량을 줄이고 SSv2에서 SOTA를 찍었다.

위의 Transformer 기반 Video 모델들은 global self-attention 모듈에 기초한다. 이렇게 하는 대신 Swin Transformer를 기반으로 문제를 해결하는 논문이 최근 올라와 있다.

이 글에서는 Contrastive Learning을 간략하게 정리한다.

Contrastive Learning

어떤 item들의 “차이”를 학습해서 그 rich representation을 학습하는 것을 말한다. 이 “차이”라는 것은 어떤 기준에 의해 정해진다.

Contrastive Learning은 Positive pair와 Negative pair로 구성된다. 단, Metric Learning과는 다르게 한 번에 3개가 아닌 2개의 point를 사용한다.

한 가지 예시는,

• 같은 image에 서로 다른 augmentation을 가한 다음
• 두 positive pair의 feature representation은 거리가 가까워지도록 학습을 하고
• 다른 image에 서로 다른 augmentation을 가한 뒤
• 두 negative pair의 feature representation은 거리가 멀어지도록 학습을 시키는

방법이 있다. 아래에서 간략히 소개할 SimCLR도 비슷한 방식이다.

Pair-wise Loss function을 사용하는데, 어떤 입력 쌍이 들어오면, ground truth distance $Y$는 두 입력이 비슷(similar)하면 0, 그렇지 않으면(dissmilar) 1의 값을 갖는다.

Loss function은 일반적으로 다음과 같이 나타낼 수 있다.

[\mathcal{L}(W) = \sum^P_{i=1} L(W, (Y, \vec{X_1}, \vec{X_2})^i)]

[L(W, (Y, \vec{X_1}, \vec{X_2})^i) = (1-Y)L_S(D^i_W) + YL_D(D^i_W)]

이때, 비슷한 경우와 그렇지 않은 경우 loss function을 다른 함수를 사용한다.

예를 들면,

[L(W, (Y, \vec{X_1}, \vec{X_2})^i) = (1-Y)\frac{1}{2}(D_W)^2 + (Y)\frac{1}{2}( \max(0, m-D_W) )^2]

즉 similar한 경우 멀어질수록 loss가 커지고, dissimilar한 경우 가까워질수록 loss가 커진다.

SimCLR(A Simple Framework for Contrastive Learning of Visual Representations)

논문 링크: A Simple Framework for Contrastive Learning of Visual Representations

Github: https://github.com/google-research/simclr

• 2020년 2월(Arxiv), ICML
• Google Research
• Ting Chen, Simon Kornblith, Mohammad Norouzi, Geoffrey Hinton

Mini-batch에 $N$개의 image가 있다고 하면, 각각 다른 종류의 augmentation을 적용하여 $2N$개의 image를 생성한다. 이때 각 이미지에 대해, 나머지 $2N-1$개의 이미지 중 1개만 positive고 나머지 $2N-2$개의 image는 negative가 된다. 이렇게 하면 anchor에 대해 positive와 negative를 어렵지 않게 생성할 수 있고 따라서 contrastive learning을 수행할 수 있다.

위의 그림을 보면.

1. 이미지 $x$에
2. 서로 다른 2개의 augmentation을 적용하여 $\tilde{x}_i, \tilde{x}_j$을 생성
3. 이는 CNN 기반 network $f(\cdot)$를 통과하여 visual representation $h_i, $h_j$로 변환됨
4. 이 표현을 projection head, 즉 MLP 기반 network인 $g(\cdot)$을 통과하여 $z_i, z_j$를 얻으면
5. 이 $z_i, z_j$로 contrastive loss를 계산한다.
6. 위에서 설명한 대로 mini-batch 안의 $N$개의 이미지에 대해 positive와 negative를 정해서 계산한다.

Contrastive loss는 다음과 같이 쓸 수 있다. (NT-Xent(Normalized Temperature-scaled Cross Entropy))

[\ell_{(i, j)} = -\log \frac{\exp(\text{sim}(z_i, z_j) / \tau)}{\sum^{2N}{k=1} \mathbb{1}{[k \ne i]} \exp(\text{sim}(z_i, z_j) / \tau)}]

참고로 이는 self-supervised learning이다(사전에 얻은 label이 필요 없음을 알 수 있다).

Miscellaneous

• Projection head는 2개의 linear layer로 구성되어 있고, 그 사이에는 ReLU activation을 적용한다.
• Batch size가 클수록 많은 negative pair를 확보할 수 있으므로 클수록 좋다. SimCLR에서는 $N=4096$을 사용하였다.
• SGD나 Momemtum 등을 사용하지 않고 대규모 batch size를 사용할 때 좋다고 알려진 LARS optimizer를 사용하였다.
• Multi-device로 분산학습을 했는데, Batch Norm을 적용할 때는 device별로 따로 계산하지 않고 전체를 통합하여 평균/분산을 계산했다. 이러면 전체 device 간의 분포를 정규화하므로 정보 손실을 줄일 수 있다.
• Data Augmentation은
  • Cropping/Resizing/Rotating/Cutout 등 이미지의 구도나 구조를 바꾸는 연산과
  • Color Jittering, Color Droppinog, Gaussian Blurring, Soble filtering 등 이미지의 색깔을 변형하는 2가지 방식을 제안하였다.
  • Augmentation 방법을 1개만 하는 것보다는 여러 개 하는 경우가 prediction task의 난이도를 높여 더 좋은 representation을 얻을 수 있다.
  • 7가지의 data augmentation 방법 중 Random crop + Random Color Distortion 방식을 적용하면 가장 좋은 성능을 보인다고 한다.

Experiments

ImageNet에서 같은 모델 크기 대비 훨씬 좋은 성능을 보인다.

3가지 방법으로 평가한 결과는 아래 표에서 볼 수 있다.

1. 학습된 모델을 고정하고 linear classifier를 추가한 linear evaluation
2. 학습된 모델과 linear classifier를 모두 학습시킨 fine-tuning
3. 학습된 모델을 다른 dataset에서 평가하는 transfer learning

ImageNet 말고 다른 dataset에서 평가한 결과는 아래와 같다. Supervised 방식과 비등하거나 더 좋은 결과도 보여준다.

SimCLR v2(Big Self-Supervised Models are Strong Semi-Supervised Learners)

논문 링크: A Simple Framework for Contrastive Learning of Visual Representations

Github: https://github.com/google-research/simclr

• 2020년 6월(Arxiv), NIPS
• Google Research
• Ting Chen, Simon Kornblith, Kevin Swersky, Mohammad Norouzi, Geoffrey Hinton

SimCLR를 여러 방법으로 개선시킨 논문이며, computer vision에서 unsupervised learning 연구에 큰 기여를 했다.

모델은 다음과 같은 과정을 따른다.

1. Unsupervised(Self-supervised) Pre-training
2. Supervised Fine-tuning
3. Distillation using unlabeled data

이때 Unsupervsed 과정에서는 최종 task와는 무관한 데이터를 사용하였기에 task-agnostic이라는 용어를 사용한다.

Unsupervised(Self-supervised) Pre-training

대량의 unlabeled dataset으로 CNN model을 학습시켜 general representation을 모델이 학습하게 된다. SimCLR와 비슷하지만 다른 점은 SimCLRv1은 projection head를 버리고 downstream task를 수행하지만 v2는 1번째 head까지 포함시켜 fine-tuning이 시작된다.
또한 Projection head의 linear layer 개수도 2개에서 3개로 늘었다.

그 이유는 label fraction(label이 되어 있는 비율)이 낮을수록 projection head의 layer가 더 많을수록 성능이 높아지기 때문이라고 한다.

Supervised Fine-tuning

전술했듯 Projection head의 1번째 layer까지 포함하여 fine-tuning을 진행한다.

Distillation via unlaeled dataset

다음 과정을 통해 distillation을 수행한다.

• 학습시킬 모델은 student model이다.
• fine-tuning까지 학습된 teacher model을 준비한다. 이때 student model의 크기는 teacher보다 작다.
• Unlabeled data를 teacher model과 student model에 집어넣고 teacher model의 output distribution을 얻는다. 여기서 가장 높은 값의 pseudo-label을 얻고 이를 student model의 output distribution과 비교하여 loss를 minimize한다.

이 과정을 통해 teacher model이 갖고 있는 지식을 student model이 학습할 수 있게 된다. 그러면서 크기는 더 작기 때문에 효율적인 모델을 만들 수 있는 것이다.

Ground-truth label과 조합하여 가중합 loss를 계산할 수도 있다.

Experiments

더 큰 모델이 더 좋은 성능을 내는 건 어쩔 수 없는 것 같다..

한 가지 눈여겨볼 것은 큰 모델일수록 label fraction이 낮은 dataset에 대해서 더 좋은 성능을 보인다는 것이다.

• 또 Projection head를 더 깊게 쌓거나 크기가 클수록 Representation을 학습하는 데 더 도움이 된다.
• Unlabeled data로 distillation을 수행하면 semi-supervised learning을 향상시킬 수 있다. 이때 label이 있는 경우 같이 사용해주면 좋은데, label이 있는 것와 없는 것을 따로 학습시키기보다는 distillation loss로 위에서 언급한 것처럼 가중합시킨 loss를 사용하면 성능이 가장 좋은 것을 확인할 수 있다.

References

• NCE loss

이 글에서는 Metric Learning을 간략하게 정리한다.

Metric Learning

한 문장으로 요약하면,

• Object간에 어떤 거리 함수를 학습하는 task

이다.

예를 들어 아래 이미지들을 보자.

뭔가 “이미지 간 거리”를 생각해보면, 1번째 이미지와 2번째 이미지는 거리가 가까울 것 같다. 이와는 대조적으로, 3번째 이미지는 다른 두 개의 이미지보다 거리가 멀 것 같다.

이런 관계를 학습하는 방식이 Metric Learning이다.

위의 경우는 조금 fine-grained한 경우이고, 좀 더 coarse한 경우는,

1번과 2번 간 거리보다는 3번 간 거리가 훨씬 멀 것 같다.

Training Dataset

그러면, 이러한 관계를 어떻게 데이터셋으로 만들 수 있는가?

• “1번 이미지가 3번 이미지보다는 2번 이미지와 더 가깝다.”

혹은

• 연관도 순으로 1 » 2 » 3 » 4

와 같이 쓸 수도 있고, 어떤 식으로든 관계를 설정해서 데이터셋으로 쓸 수 있다.

그렇다면, 왜 이렇게 복잡해 보이는(?) 방식으로 데이터를 구성하고 학습을 시키는가?

당연히, 이러한 데이터셋은 hard하게 labeling하는 것보다 훨씬 쉽게 대량의 데이터를 구성할 수 있다.

그리고, 위와 같이 어쨌든 supervision이 있기 때문에(좀 약하긴 하지만) metric learning은 지도학습의 일종이다.

Problem Formulation

크게 3가지로 생각할 수 있다. 이 중 일반적으로 2번째가 많이 쓰인다.

1. Point-wise Problem: 하나의 학습 샘플은 Query-Item 쌍이 있고 어떤 numerical/ordinal score와 연관된다.
   • 그냥 classification 문제와 비슷하다. 하나의 query-item 쌍이 주어지면, 모델은 그 score를 예측할 수 있어야 한다.
2. Pair-wise Problem: 하나의 학습 샘플은 순서가 있는 2개의 item으로 구성된다.
   • 모델은 주어진 query에 대해 각 item에 점수(혹은 순위)를 예측한다. 순서는 보존된다.
   • 그 순위(순서)를 최대한 바르게 맞추는 것이 목표가 된다.
3. List-wise Problem: 하나의 학습 샘플이 2개보다 많은 item의 순서가 있는 list로 구성된다.
   • 계산량이 많고 어려워서 많이 쓰이지는 않는다.
   • NDCG 등으로 평가한다.

NDCG(Normalized Discounted Cumulative Gain)

널리 쓰이는 ranking metric(순위 평가 척도)이다.

먼저 CG를 정의한다.

Cumulative Gain: result list에서 모든 result의 관련도 점수의 합. $rel_i$는 관계가 제일 높으면 1, 그 반대면 0이라 할 수 있다. 물론 0~1 범위가 아니라 실제 점수를 쓸 수도 있다.

[\text{CG}p = \sum^p{i=1}rel_i]

이제 DCG를 정의하자. Discounted CG는 상위에 있는 item을 더 중요하게 친다.

[\text{DCG}p = \sum^p{i=1} \frac{rel_i}{\log_2(i+1)} = rel_1 + \sum^p_{i=2} \frac{rel_i}{\log_2(i+1)}]

Alternative formulation of DCG를 생각할 수도 있다. 이는 관련도상 상위 item을 더 강조한다.

[\text{DCG}p = \sum^p{i=1} \frac{2^{rel_i}-1}{\log_2(i+1)}]

그런데 DCG는 개수가 많거나 관련도 점수가 높으면 한없이 커질 수 있다. 그래서 정규화가 필요하다.

이제 Normalized DCG를 정의하자. 그러러면 먼저 Ideal DCG를 생각해야 한다. IDCG는 위의 식으로 최상의 결과를 출력했을 때 얻을 수 있는 점수라 생각하면 된다.

[\text{DCG}p = \sum^{REL_p}{i=1} \frac{rel_i}{\log_2(i+1)}]

이제 NDCG는 다음과 같다.

[\text{NDCG}_p = \frac{DCG_p}{IDCG_p}]

Triplet Loss

3개의 point 간 거리를 갖고 loss를 구하는 방식이다.

• 기준점을 Anchor,
• anchor와 관련이 높은 point를 Positive,
• 관련이 없거나 먼 point를 Negative

라 하면,

loss function은 유클리드 거리 함수로 생각할 수 있다.

[\mathcal{L}(A, P, N) = max(\Vert \text{f}(A) - \text{f}(P) \Vert^2 - \Vert \text{f}(A) - \text{f}(N) \Vert^2 + \alpha, 0)]

$N$개의 anchor point로 확장하면 다음과 같이 쓸 수 있다. (사실 같은 식이라 다름없다)

[\mathcal{L} = \sum^N_i [ max(\Vert \text{f}(x_i^a) - \text{f}(x_i^p) \Vert^2 - \Vert \text{f}(x_i^a) - \text{f}(x_i^n) \Vert^2 + \alpha, 0)]]

$\alpha$는 margin을 나타낸다.

Training(Dataset)

학습할 때 anchor과 positive, negative를 잘 설정해야 한다.

랜덤으로 point를 뽑으면 잘 되지 않는 경우가 많다.

여기서 사용할 수 있는 방법으로 Online Negative Mining이 있다.

이는 batch를 크게 잡아서, 현재 sample인 anchor-positive-negative에서 다른 sample의 anchor/positive/negative 중 anchor와 positive 관계인 것을 제외하고 가장 가까운 것부터 선택하여 negative를 대체하여 계산할 수 있다. 이러면 학습이 조금 더 되지만, batch size가 커야 되고, 계산량이 매우 많아지는 단점이 존재한다.

학습을 더 잘 하기 위해서 생각해야 할 방법은 semi-hard negative mining이다.

A와 P는 고정이라 할 때, 아래 3개의 Negative 중 어느 것을 선택해야 학습이 잘 될까라는 문제이다.

• Hard Negative: $d(a, n_1) < d(a, p)$
  • 언뜻 보면 학습이 잘 될 것 같지만, loss를 줄이는 방법은 그냥 모든 $x$에 대해 $f(x)=0$으로 만들어 버리는 것이라(collapsing) 학습이 잘 안 된다.
• Semi-hard Negative: $d(a, p) < d(a, n_2) < d(a, p) + \alpha$
  • 이 경우에는 위의 collapsing problem이 발생하지 않으면서 N을 P 밖으로 밀어내면서 학습이 제일 잘 된다.
• Easy Negative: $d(a, p) + \alpha < d(a, n_3)$
  • N3는 이미 $d(a, p) + \alpha$보다 멀리 있기 때문에 negative로 잡아도 학습할 수 있는 것이 없다.

따라서 semi-hard negative로 sample을 잡아 학습하는 것이 제일 좋다고 한다.

FaceNet: A Unified Embedding for Face Recognition and Clustering

논문 링크: FaceNet: A Unified Embedding for Face Recognition and Clustering

Metric Learning을 사용해서 여러 사진이 있을 때 같은 사람의 사진끼리 모으는 task를 수행했다.

이 글에서는 Attention 기반 Video (Classification) Model을 간략히 소개한다.

Multi-LSTM

논문 링크: Every Moment Counts: Dense Detailed Labeling of Actions in Complex Videos

LRCN과 비슷하다.

다른 점은,

• Multiple Input: LSTM에 입력이 1개의 frame이 아니라 N개의 최근 frame에 대해 attention을 적용한다.
  • Query: LSTM의 이전 hidden state $h_{i-1}$
  • Key=value: $N$개의 input frame features
  • Attention value: $N$개의 frame freature의 가중합
• Multiple Output: 각 LSTM cell은 $N$개의 최근 frame에 대한 예측결과를 출력한다.

Action Recognition using Visual Attention

논문 링크: Action Recognition using Visual Attention

• LSTM의 이전 hidden state(=query)와 입력 이미지의 region feature(7 x 7 x 1024)를 49개의 candidate로 보고 spatial attention을 수행한다. 이를 통해 attention value(1024차원)를 얻는다.
  • Query: LSTM의 직전 hidden state
  • Key=Value: 입력 이미지 $X_t$의 $K \times K$의 region feature
  • Attention Value: region feature의 가중합. Weight: $h_{t-1}$

이 모델의 장점은 Interpretability가 좋다(spatial attention에 의함). 정답을 맞췄을 때 어떤 부분을 보고 맞추었는지, 혹은 반대로 틀렸을때 어디를 보고 틀렸는지를 볼 수 있다(spatial attention의 의미를 생각해보면 알 수 있다).